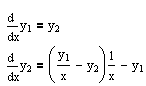Решить дифференциальное уравнение второго порядка матлаб (4 видео)

Решение ОДУ в Matlab

Доброго времени суток! Сегодня мы поговорим о решении ОДУ (обыкновенных дифференциальных уравнений) в Matlab. Перед тем как мы начнём обсуждать данную тему, советую вам ознакомиться с темой: Численное дифференцирование в Matlab, чтобы лучше понимать теоретическую составляющую решения ОДУ.

Содержание

Обыкновенные дифференциальные уравнения
Методы решения дифференциальных уравнений
Метод Рунге-Кутта первого порядка
Метод Рунге-Кутта второго порядка
Метод Рунге-Кутта четвёртого порядка
Решение ОДУ в Matlab стандартными средствами
Решить дифференциальное уравнение второго порядка матлаб
Решатели (solver) ОДУ в MATLAB
🎬 Видео

Обыкновенные дифференциальные уравнения

С помощью дифференциальных уравнений можно описать разные задачи: движения системы, взаимодействующих материальных точек, химической кинетики и т.д. Различают три типа задач для систем диф. уравнений:

Задача Коши
Краевая задача
Задача на собственные значения

Кратко расскажу о их сути:

Задача Коши предполагает дополнительные условия в виде значения функции в определённой точке.
Краевая задача подразумевает поиск решения на заданном отрезке с краевыми (граничными) условиями в концах интервала или на границе области.
Задача на собственные значения — помимо искомых функций и их производных, в уравнение входят дополнительное несколько неизвестных параметров, которые являются собственными значениями.

Видео:Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

Методы решения дифференциальных уравнений

Решение ОДУ в Matlab и не только, в первую очередь, сводится к выбору порядка численного метода решения. Порядок численного метода не связан с порядком дифференциального уравнения. Высокий порядок у численного метода означает его скорость сходимости.

В случае большого интервала, с помощью алгоритмов с низким порядком сжимают интервал с решениями и находят приблизительные корни, а затем уже уточняют корни с помощью методов с высоким порядком.

Решение обыкновенных дифференциальных уравнений в Matlab можно реализовать «своими ручками», прописав алгоритм по разным схемам. Но также в Matlab есть встроенные функции, выполняющие все стандартные задачи.

Метод Рунге-Кутта первого порядка

Методы Рунге-Кутта представляют собой разложения в ряд Тейлора и от количества использованных элементов ряда зависит порядок этого метода. Следовательно, помимо Рунге-Кутта первого порядка, вы сможете увидеть методы других порядков. Иногда их называют другими именами.

Например, Метод Рунге-Кутта первого порядка, также известен как Метод Эйлера или Метод ломаных. Информацию о его математическом и графическом представлении советую поискать в гугл. Мы же поговорим о том, как Метод Рунге-Кутта первого порядка реализуется в Matlab для решения ОДУ. Например:

Решить и привести график ошибки уравнения y’ = y*x методом Рунге-Кутта первого порядка (Методом Эйлера, Методом ломаных).

Погрешность Метода Рунге-Кутта 1 порядка

» data-medium-file=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?fit=300%2C236&ssl=1″ data-large-file=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?fit=622%2C489&ssl=1″ loading=»lazy» src=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/%D0%A0%D1%83%D0%BD%D0%B3%D0%B5-1-%D0%BF%D0%BE%D0%B3%D1%80%D0%B5%D1%88%D0%BD%D0%BE%D1%81%D1%82%D1%8C.png?resize=622%2C489″ alt=»Погрешность метода 1 порядка» width=»622″ height=»489″ srcset=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?w=629&ssl=1 629w, https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?resize=300%2C236&ssl=1 300w» sizes=»(max-width: 622px) 100vw, 622px» data-recalc-dims=»1″ />
На данном графике показана зависимость величины ошибки от шага.

Метод Рунге-Кутта второго порядка

Также известен как Метод Эйлера-Коши. Как видите, во второй части уравнения происходит обращения к следующему шагу. Но как тогда быть, если нам ещё не известен следующий шаг? Всё просто. Метод Рунге-Кутта второго порядка — это всё тот же метод первого порядка, однако, на половине шага происходит нахождение «первичного» решения, а затем происходит его уточнение. Это позволяет поднять порядок скорости сходимости до двух.

Решить и привести график ошибки уравнения u’ = u*x методом Рунге-Кутта второго порядка.

По сравнению с Рунге-Куттом первого порядка изначальная ошибка уже гораздо меньше.

Мы не будем говорить о третьем порядке, потому что задачи на третий порядок встречаются редко, но если будет необходимо, пишите в комментариях, выложу.

Метод Рунге-Кутта четвёртого порядка

Метод Рунге-Кутта четвёртого порядка считается самым распространённым. Тем не менее, работает он аналогично второму и третьему порядку.

Решить и привести график ошибки уравнения u’ = u*x методом Рунге-Кутта четвёртого порядка.

Как видите, на последней картинке размерность ошибки на столько мала, что пришлось воспользоваться loglog() для лучшей видимости.

Решение ОДУ в Matlab стандартными средствами

Стоит отметить, что мы с вами разобрали только один самый известный метод решения ОДУ с разными порядками. Однако, методов очень много.

Для решения дифференциальных уравнений и систем в MATLAB предусмотрены следующие функции:

ode45 (f, interval, X0, [options])
ode23 (f, interval, X0, [options])
ode113 (f, interval, X0, [options])
ode15s (f, interval, X0, [options])
ode23s (f, interval, X0, [options])
ode23t (f, interval, X0, [options])
ode23tb (f, interval, X0, [options])

Входными параметрами этих функций являются:

f — вектор-функция для вычисления правой части уравнения системы уравнений;
interval — массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы;
Х0 — вектор начальных условий системы дифференциальных уравнений;
options — параметры управления ходом решения дифференциального уравнения или системы.

Все функции возвращают:

массив Т — координаты узлов сетки, в которых ищется решение;
матрицу X, i-й столбец которой является значением вектор-функции решения в узле Тi.

В функции ode45 реализован метод Рунге-Кутта 4-5 порядка точности, в функции ode23 также реализован метод Рунге-Кутта, но 2-3 порядка, а функция ode113 реализует метод Адамса.

Для решения жёстких систем предназначены функция ode15s, в которой реализован метод Гира, и функция ode23s, реализующая метод Розенброка. Для получения более точного решения жёсткой системы лучше использовать функцию ode15s. Для решения системы с небольшим числом жёсткости можно использовать функцию ode23t, а для грубой оценки подобных систем служит функция ode23tb.

Символьное решение обыкновенных дифференциальных уравнений произвольного порядка осуществляет функция dsolve r = dsolve(‘eq1,eq2,…’, ‘cond1,cond2,…‘, ‘v’)
Пример использования:

На этом мы закончим. Если остались вопросы, задавайте их в комментариях. Также вы можете скачать исходники чтобы лучше понять тему: «Решение ОДУ в Matlab».

Видео:Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

Решить дифференциальное уравнение второго порядка матлаб

Дифференциальные уравнения и системы уравнений

Для решения дифференциальных уравнений и систем в MATLAB предусмотрены следующие функции ode45(f, interval, X0 [, options]), ode23(f, interval, X0 [, options]), ode113(f, interval, X0 [, options]), odel5s(f, interval, X0 [, options]), ode23s(f, interval, X0 [, options]), ode23t (f, interval, X0 [,options]) и ode23tb(f, interval, X0 [, options]).

Входными параметрами этих функций являются:

f — вектор-функция для вычисления правой части уравнения системы уравнений
interval — массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы;
Х0 — вектор начальных условий системы дифференциальных систем
options — параметры управления ходом решения дифференциального уравнения или системы.

Все функции возвращают:

массив Т — координаты узлов сетки, в которых ищется решение;
матрицу X, i-й столбец которой является значением вектор-функции решения в узле Тi

В функции ode45 реализован метод Рунге-Кутта 4-5 порядка точности, в функции ode23 также реализован метод Рунге-Кутта, но 2-3 порядка, а функция ode113 реализует метод Адамса.

В М-файле с именем pr 7. m пишем:

Потом в командном окне вызываем функцию ode113:

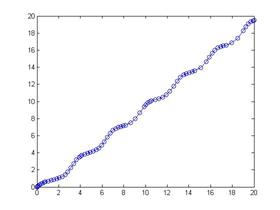
ode113(@pr7,[0 20],0) %Метод Адамса: @ pr 7 – ссылка на М-функцию, [0 20]- интервалы интегрирования,0 — условие: y(0)=0

Результатом будет график:

Необходимо реализовать метод Рунге-Кутта 4 порядка и решить задачу Коши для предложенной системы дифференциальных уравнений:

В М-файле с именем pr 8. m пишем:

Потом в командном окне вызываем функцию ode 45:

Видео:MatLab. Решение дифференциального уравнения.Скачать

Решатели (solver) ОДУ в MATLAB

Анализ поведения многих систем и устройств в динамике, а также решение многих задач в теории колебаний обычно базируется на решении систем ОДУ. Их, как правило, представляют в виде системы из дифференциальных уравнений (ДУ) первого порядка в форме Коши:

dy/dt = y′ = f(y, t)

(1.1)

с граничными условиями y(t₀, t_end, p) = y, где t_end, t₀ начальные и конечные точки интервалов. Параметр t (независимая переменная) необязательно означает время, хотя чаще всего решение ДУ ищется во временной области. Система ДУ в форме Коши записывается аналогично (1.1), но под y в этом случае подразумевается вектор-столбец зависимых переменных. Вектор p задает начальные условия.

Для решения ДУ второго и высшего порядка их нужно свести к системе ДУ первого порядка.

Возможны ДУ, не разрешенные относительно производной:

F(t, y, dy/dt) = 0.

(1.2)

Уравнения (1.2) аналитически к форме (1.1) обычно привести не удается. Однако численное решение особых трудностей не вызывает достаточно для определения f(y, t) решить (1.2) численно относительно производной при заданных y и t.

Решатели ОДУ

Для решения систем ОДУ в MATLAB реализованы различные численные методы. Их реализации названы решателями ОДУ.

В этом разделе обобщенное название solver (решатель) означает один из возможных численных методов решения ОДУ: ode45, ode23, ode113, ode15s, ode23s, ode23t, ode23tb, bvp4c или pdepe.

Решатели реализуют следующие методы решения систем ДУ:

• ode45 одношаговые явные методы Рунге-Кутта 4-го и 5-го порядков в модификации Дорманда и Принца. Это классический метод, рекомендуемый для начальной пробы решения. Во многих случаях он дает хорошие результаты, если система решаемых уравнений нежесткая.

• ode23 одношаговые явные методы Рунге-Кутта 2-го и 4-го порядков в модификации Богацки и Шампина. При умеренной жесткости системы ОДУ и низких требованиях к точности этот метод может дать выигрыш в скорости решения.

• ode113 многошаговый метод Адамса-Башворта-Мултона переменного порядка класса предиктор-корректор. Это адаптивный метод, который может обеспечить высокую точность решения.

• ode15s многошаговый метод переменного порядка (от 1 до 5, по умолчанию 5), использующий формулы численного «дифференцирования назад». Это адаптивный метод, его стоит применять, если решатель ode45 не обеспечивает решения и система ДУ жесткая.

• ode23s одношаговый метод, использующий модифицированную формулу Розенброка 2-го порядка. Может обеспечить высокую скорость вычислений при низкой точности решения жесткой системы ДУ.

• ode23t неявный метод трапеций с интерполяцией. Этот метод дает хорошие результаты при решении задач, описывающих колебательные системы с почти гармоническим выходным сигналом. При умеренно жестких системах ДУ может дать высокую точность решения.

• ode23tb неявный метод Рунге Кутта в начале решения и метод, использующий формулы «дифференцирования назад» 2-го порядка в последующем. Несмотря на сравнительно низкую точность, этот метод может оказаться более эффективным, чем ode15s.

• bvp4c служит для проблемы граничных значений систем ДУ вида y′ = f(t, y), F(y(a), y(b), p) = 0 (полная форма системы уравнений Коши). Решаемые им задачи называют двухточечными краевыми задачами, поскольку решение ищется при задании граничных условий как в начале, так и в конце интервала решения.

Все решатели могут решать системы уравнений явного вида y′ = F(t, y), причем для решения жестких систем уравнений рекомендуется использовать только специальные решатели ode15s, ode23s, ode23t, ode23tb.

Использование решателей систем ОДУ

В описанных далее функциях для решения систем ДУ приняты следующие обозначения и правила:

• tspan вектор, определяющий интервал интегрирования [t₀ t_final]. Для получения решений в конкретные моменты времени t₀, t₁, …, t_final (расположенные в порядке уменьшения или увеличения) нужно использовать tspan = [_t₀ t₁ … t_final];

• y₀ вектор начальных условий;

• options аргумент, создаваемый функцией odeset (еще одна функция odeget или bvpget (только для bvp4c) позволяет вывести параметры, установленные по умолчанию или с помощью функции odeset/bvpset);

• p1, p2,… произвольные параметры, передаваемые в функцию F;

• T, Y матрица решений Y, где каждая строка соответствует времени, возвращенном в векторе-столбце T.

Перейдем к описанию синтаксиса функций для решения систем ДУ (под именем solver подразумевается любая из представленных выше функций).

• [T,Y]=solver(@F,tspan,y₀) интегрирует систему ДУ вида y′ = F(t, y) на интервале tspan с начальными условиями y₀. @F дескриптор ОДУ-функции (можно также задавать функцию в виде ‘F‘). Каждая строка в массиве решений Y соответствует значению времени, возвращаемому в векторе-столбце T.

• [T,Y]=solver(@F,tspan,y₀,options) дает решение, подобное описанному выше, но с параметрами, определяемыми значениями аргумента options, созданного функцией odeset. Обычно используемые параметры включают допустимое значение относительной погрешности RelTol (по умолчанию 1e3) и вектор допустимых значений абсолютной погрешности AbsTol (все компоненты по умолчанию равны 1e6).

• [T,Y]=solver(@F,tspan,y₀,options,p₁,p₂…) дает решение, подобное описанному выше, передавая дополнительные параметры p₁, p₂, … в m-файл F всякий раз, когда он вызывается. Используйте options=[], если никакие параметры не задаются.

Решение ОДУ первого порядка

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Изучить теоретическую часть. Выполните задания, соответствующие номеру Вашего варианта, и продемонстрируйте их преподавателю.

2. Оформите отчет по лабораторной работе, который должен содержать:

· исходные данные варианта;

· результаты решения задачи.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

Пример

Найти решение дифференциального уравнения на отрезке [1,7; 2,7], для которого у(1,7) = 5,3.

Создаем в Command Window функция пользователя

В синтаксисе функции @(x,y) x независимая переменная, y зависимая переменная, x-cos(y/pi) правая часть ДУ.

Процесс решения осуществляется обращением в Command Window к решателю (солверу) следующим оператором:

Построение графика с сеткой осуществляется следующими операторами:

Результат представлен на рис. 1.1

Рис. 1.2.1. Визуализация численного решения

ЗАДАНИЕ

1. Найдите решения ДУ первого порядка 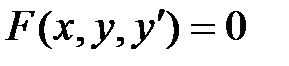, удовлетворяющего начальным условиям у(х₀) = у₀ на промежутке [a, b].

2. Построить графики функции.

№ варианта		у(х₀)=у₀	[a, b]
	y₀(1,8)=2,6	[1,8; 2,8]
	y₀(0,6)=0,8	[0,6; 1,6]
	y₀(2,1)=2,5	[2,1; 3,1]
	y₀(0,5)=0,6	[0,5; 1,5]
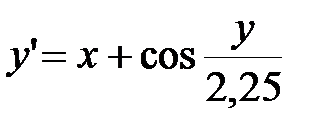	y₀(1,4)=2,2	[1,4; 2,4]
	y₀(1,7)=5,3	[1,7; 2,7]
	y₀(1,4)=2,5	[1,4; 2,4]
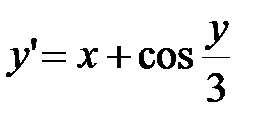	y₀(1,6)=4,6	[1,6; 2,6]
	y₀(1,8)=2,6	[1,8; 2,8]
	y₀(1,7)=5,3	[1,7; 2,7]
	y₀(0,4)=0,8	[0,4; 1,4]
	y₀(1,2)=1,4	[1,2; 2,2]

Лабораторная работа № 2

Решение систем ОДУ

ЦЕЛЬ РАБОТЫ

Сформировать у студентов представления о применении систем ДУ в различных областях; привить умения решать задачу Коши для систем ДУ.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

2. Оформите отчет по лабораторной работе, который должен содержать:

· исходные данные варианта;

· результаты решения задачи.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

Пример

Решить систему при данных начальных условиях с использованием решателя ode23().

Решение:

1. Создать в редакторе m-файл функции вычисления правых частей ДУ.

Пусть имя в редакторе файла sisdu.m, тогда функция может иметь следующий вид:

2. Выполнить следующие действия:

Рис. 1.3.1. Визуализация численного решения, полученного с помощью функции ode23.

ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ

1. Что значит решить задачу Коши для системы ДУ?

2. Какие существуют методы решения систем ДУ?

ЗАДАНИЕ

1. Найдите решение системы ДУ

удовлетворяющее начальным условиям 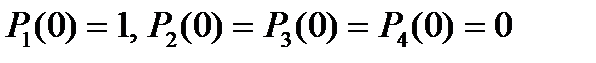на промежутке [0, 1];

2. Построить графики функций.

Для примера приводится функция решения 8-го варианта:

>> [t,y]=ode23(‘ssisdu’,[0 1],[1 0 0 0]);

Рис. 1.3.2. Визуализация численного решения, полученного с помощью функции ode23.

№ варианта	Задания
a	m
0,1	1,2
0,2	1,5
0,3	1,7
0,4	1,9
0,5
0,6	1,9
0,7	2,3
0,8	2,7
0,9
0,1	1,5
0,2	1,1
0,3

Лабораторная работа № 3

1.4Решение ОДУ n-го порядка

ЦЕЛЬ РАБОТЫ

Сформировать у студентов представления о применении ДУ высших порядков в различных областях; привить умения решать задачу Коши для ДУ высших порядков с помощью прикладных программ; развить навыки проверки полученных результатов.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

2. Оформите отчет по лабораторной работе, который должен содержать:

· исходные данные варианта;

· результаты решения задачи.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

Пример 1.

Решить ДУ второго порядка при данных начальных условиях .

Решение:

Сначала приведем ДУ к системе:

1. Создать m-файл функции вычисления правых частей ДУ.

Пусть имя файла sisdu_3.m, тогда функция может иметь следующий вид:

2. Выполнить следующие действия:

Рис. 1.4.1. Визуализация численного решения, полученного с помощью функции ode23.

ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ

1. Что значит решить задачу Коши для ДУ высших порядков?

2. Как привести ДУ m-го порядка к системе ДУ?

ЗАДАНИЕ

1. Найдите решение ДУ, удовлетворяющее начальным условиям на промежутке [0, 10].

2. Построить графики функций.

№ варианта	Задания
Уравнения	Начальные условия

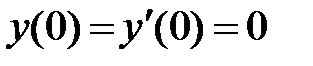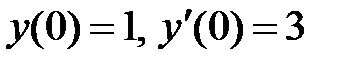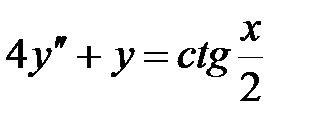Лабораторная работа № 4 – 5

Динамические системы (ДС)

ЦЕЛЬ РАБОТЫ

Знакомство студентов с основными понятиями ДС, их классификация, фазовое пространство ДС, кинематическая интерпретация системы ДУ, эволюция ДС. Уравнение движения маятника. Динамика осциллятора Ван дер Поля.

2. Динамическая система (ДС) математический объект, соответствующий реальным системам (физическим, химическим, биологическим и др.), эволюция которых однозначно определяется начальным состоянием. ДС определяется системой уравнений (дифференциальных, разностных, интегральных и т.д.), допускающих существование на бесконечном интервале времени единственность решения для каждого начального условия.

Состояние ДС описывают набором переменных, выбираемых из соображений естественности их интерпретации, простоты описания, симметрии и т.п. Множество состояний ДС образует фазовое пространство, каждому состоянию отвечает точка в нём, а эволюция изображается (фазовыми) траекториями. Чтобы определить близость состояний, в фазовом пространстве ДС вводят понятие расстояния. Совокупность состояний в фиксированный момент времени характеризуется фазовым объёмом.

Описание ДС в смысле задания закона эволюции также допускает большое разнообразие: оно осуществляется с помощью дифференциальных уравнений, дискретных отображений, с помощью теории графов, теории марковских цепей и т.д. Выбор одного из способов описания задает конкретный вид математической модели соответствующей ДС.

Математическая модель ДС считается заданной, если введены динамические переменные (координаты) системы, определяющие однозначно ее состояние, и указан закон эволюции состояния во времени.

В зависимости от степени приближения одной и той же системе могут быть поставлены в соответствие различные математические модели. Исследование реальных систем идет по пути изучения соответствующих математических моделей, совершенствование и развитие которых определяется анализом экспериментальных и теоретических результатов при их сопоставлении. В связи с этим под динамической системой мы будем понимать именно ее математическую модель. Исследуя одну и ту же ДС (к примеру, движение маятника), в зависимости от степени учета различных факторов мы получим различные математические модели.