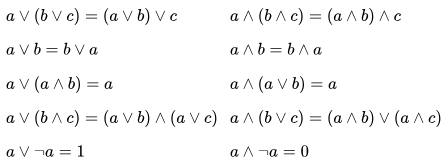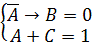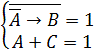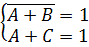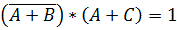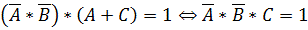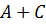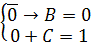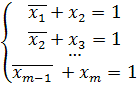Решить булево уравнение примеры с решением (6 видео)

Булевы функции и формулы

В этом разделе вы найдете бесплатные примеры решений базовых задач по булевым формулам (формулам булевой алгебры): упрощение формул, проверка на тавтологию, преобразование к виду без скобок, проверка фиктивности переменной, доказательство эквивалентности булевых формул и т.п.

В следующих разделах вы найдете другие примеры решений о булевых функциях:

Содержание

Решения задач по булевым формулам онлайн
Булева алгебра для чайников
Булева алгебра
Логические операции
Приоритет логических операций
Булевы алгебры и полукольца
Свойства симметричного полукольца
Свойства булевых алгебр
Примеры булевых алгебр
Решить булево уравнение примеры с решением
📸 Видео

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Решения задач по булевым формулам онлайн

Задача 1. Проверить, является ли тавтологией формула: $a & b to(a & b vee c vee bar c)$

Задача 2. Преобразовать данную формулу так, чтобы она содержала только операции тесного отрицания, дизъюнкции и конъюнкции. Пользуясь свойствами операций дизъюнкции и конъюнкции, привести формулу к виду, не содержащему скобок.

$$(overline vee x_2) to (overline sim x_3)overline $$

Задача 3. Показать, что $x_1$ — фиктивная переменная функции $f$ (реализовав для этой цели функцию $f$ формулой, не содержащей явно переменную $x_1$).

Задача 4. Используя приведенные ниже (основные) эквивалентности и соотношения, доказать эквивалентность формул $U$ и $B$.

Задача 5. Классифицировать формулу $overline< (overlineto x) vee y>$

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Булева алгебра для чайников

Булева алгебра

Булевой алгеброй называется непустое множество $A$ с двумя бинарными операциями $land$ (аналог конъюнкции), $lor $ (аналог дизъюнкции), одной унарной операцией $lnot$ (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для любых a, b и c из множества A верны следующие аксиомы:

Логические операции

В алгебре логики основными (элементарными) операциями являются отрицание, логическое сложение (дизъюнкция), логическое умножение (конъюнкция), импликация, эквивалентность.

Основные формулы по алгебре логики: функции алгебры логики, таблица истинности, основные эквивалентности, преобразование к конъюнкции, дизъюнкции и отрицанию

Приоритет логических операций

При упрощении булевых формул или высказываний, связанных скобками и логическими операциями, используют следующие правила приоритета (или старшинства) логических операций — от наиболее сильной — к слабой:

$$ neg quad wedge quad vee quad to quad leftrightarrow $$

Словесно: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность.

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Булевы алгебры и полукольца

Теория булевых алгебр является классическим разделом дискретной математики. Булевы алгебры возникли в трудах английского математика Дж. Буля в 50-х годах XIX века как аппарат логики. При этом элементы булевой алгебры трактовались как высказывания, а операциями являлись дизъюнкция, конъюнкция и отрицание.

Существуют различные подходы к определению булевой алгебры. Мы определим булеву алгебру как частный случай идемпотентного полукольца.

Определение 3.3. Полукольцо называют симметричным (или взаимным), если оно идемпотентно и в нем выполнены следующие тождества:

Можно дать определение, равносильное определению 3.3. Идемпотентное полукольцо называется симметричным (или взаимным), если алгебра также является идемпотентным полукольцом. При этом будем говорить, что идемпотентное полукольцо есть полукольцо, двойственное к идемпотентному полукольцу .

Из определения следует, что в двойственном идемпотентном полукольце операция сложения — это операция умножения в исходном полукольце и наоборот; нуль двойственного полукольца — это единица исходного полукольца и наоборот. Легко видеть, что полукольцо , двойственное к двойственному полукольцу , есть исходное полукольцо .

Запишем полностью все аксиомы (основные тождества) симметричного полукольца, объединяя двойственные аксиомы в пары (табл. 3.3).

В табл. 3.1 можно увидеть, что в симметричном полукольце операции сложения и умножения, равно как и элементы и , полностью „взаимозаменяемые», или взаимно двойственные.

Таким образом, справедлив принцип двойственности для симметричных полуколец: любое тождество в симметричном полукольце остается верным, если в нем операцию сложения заменить операцией умножения и наоборот, а единицу заменить нулем и наоборот.

Пример 3.8. а. Полукольцо (см. пример 3.2) симметричное.

б. Полукольцо (см. пример 3.1) не является симметричным в силу неидемпотентности умножения полукольца, хотя в нем единица полукольца (число 0) имеет аннулирующее свойство, поскольку .

в. Полукольцо (см. пример 3.3,б) симметрично в силу известных свойств операций пересечения и объединения множеств.

г. Полукольцо (см. пример 3.3,в) не является симметричным.

д. Полукольцо (см. пример З.З,г) симметрично.

Пример 3.9. Рассмотрим алгебру , где — множество всех делителей натурального числа ; — операция вычисления наименьшего общего кратного; — операция вычисления наибольшего общего делителя двух чисел. Эта алгебра является симметричным полукольцом.

Действительно, для любых двух натуральных чисел и верно представление

где — наибольший простой множитель в разложении и . Тогда

Таким образом, свойства операций и определяются свойствами операций и . В силу этого рассматриваемая алгебра и является симметричным полукольцом (см. пример 3.3,г).

Видео:Уравнения с модулемСкачать

Свойства симметричного полукольца

Рассмотрим некоторые свойства симметричного полукольца, вытекающие из его аксиом.

Свойство 3.1. Для любых элементов симметричного полукольца выполняются равенства

Равенства, приведенные в формулировке свойства 3.1, называют тождествами поглощения.

Свойство 3.2. В симметричном полукольце неравенство имеет место тогда и только тогда, когда .

Вспомним, что по определению естественного порядка произвольного идемпотентного полукольца .

Пусть . Тогда (по свойству 3.1).

Пусть теперь . Тогда . Следовательно, .

Свойство 3.2 выражает связь умножения с естественным порядком идемпотентного полукольца: меньший сомножитель поглощает больший, т.е. порядок в двойственном полукольце является порядком, двойственным к порядку в полукольце . Но, как известно, при переходе к двойственному порядку наибольший (максимальный) элемент становится наименьшим (минимальным) элементом, а точная верхняя грань — точной нижней гранью.

Свойство 3.3. В симметричном полукольце произведение есть точная нижняя грань последовательности

Свойство 3.4. Для любого элемента симметричного полукольца имеет место неравенство .

Первое неравенство равносильно равенству , верному для любого . Второе неравенство вытекает из четвертого тождества определения 3.3.

Таким образом, в симметричном полукольце единица (1) является наибольшим элементом.

Определение 3.4. Булева алгебра — это симметричное полукольцо, в котором для каждого существует элемент , называемый дополнением , такой, что

Обычно сложение в булевой алгебре называют булевым объединением и обозначают , а умножение — булевым пересечением и обозначают .

Запишем аксиомы булевой алгебры в виде табл. 3.4, объединяя «двойственные пары» (как это мы уже сделали, записывая аксиомы симметричного идемпотентного полукольца).

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Свойства булевых алгебр

Рассмотрим некоторые важные свойства булевых алгебр , вытекающие из определения.

Свойство 3.5 (единственность дополнения). В булевой алгебре для любого его дополнение единственное.

Пусть для элемента найдется еще одно такое , что и .

Имеем . Воспользовавшись свойством (3.29), получим . В силу дистрибутивности и с учетом свойств элемента имеем

С учетом свойств дополнения преобразуем последнее выражение следующим образом:

Поскольку , то . Таким образом, элемент совпадает с дополнением .

Свойство 3.6 («симметричность» операции дополнения). В булевой алгебре выполняется тождество

Так как является дополнением к , то и . В то же время и . В силу единственности дополнения к элементу имеем .

Свойство 3.7. В булевой алгебре верны следующие тождества:

В силу свойств 3.5 и 3.6 для доказательства первого закона достаточно показать, что

Преобразуя выражения в левых частях, получаем

Первое тождество доказано. Второе тождество следует из принципа двойственности.

Тождества (3.31) называют законами де Моргана для булевых алгебр.

Единственность дополнения означает, что в булевой алгебре возникает унарная операция — переход от элемента к его дополнению. Эту операцию можно ввести в сигнатуру алгебры, т.е. рассматривать булеву алгебру как алгебру вида

с двумя бинарными, одной унарной и двумя нульарными операциями, такую, что:

Дополнение в булевой алгебре называют булевым дополнением, а все операции булевой алгебры — булевыми операциями.

Видео:Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Примеры булевых алгебр

Рассмотрим теперь некоторые примеры булевых алгебр.

Пример 3.10. Полукольцо (см. пример 3.2) является булевой алгеброй. Эта булева алгебра — важнейшая структура. Мы назовем ее двухэлементной булевой алгеброй и обозначим . Видно, что в

Пример 3.11. На множестве определим структуру булевой алгебры, положив для произвольных из , что

Можно без труда показать, что все аксиомы булевой алгебры выполняются. Носитель определенной таким образом булевой алгебры называют булевым кубом размерности , а его элементы — булевыми векторами (или булевыми наборами) размерности . Вектор называют при этом нулевым булевым вектором или нулевым набором, а вектор — единичным булевым вектором или единичным набором. Заметим, что случаи и включаются в эту конструкцию. При получаем уже рассмотренную двухэлементную булеву алгебру , а при — так называемую одноэлементную булеву алгебру, в которой . Но эта структура малоинтересна.

Итак, булевы операции над булевыми векторами выполняются покомпонетно — так же, как сложение векторов или умножение вектора на число в линейной алгебре. Отношение порядка здесь определено также покомпонентно, т.е. для произвольных

неравенство означает, что . Так, например,

Пример 3.12. Полукольцо (см. пример 3.3.б) — булева алгебра, в которой все булевы операции суть не что иное, как обычные теоретико-множественные операции, т.е. булево объединение есть обычное объединение множеств, булево пересечение — пересечение множеств, булево дополнение — дополнение множества.

Пример 3.13. а. Рассмотрим полукольцо делителей числа 6 с операциями и . Из примера 3.9 следует, что это полукольцо симметричное. Нуль этого полукольца есть число 1, а единица — число 6. Убедимся, что каждый элемент полукольца имеет дополнение. Начнем с числа 1. Дополнение х должно удовлетворять равенствам и . Первое равенство означает, что , а второе — . Легко видеть, что . Рассуждая аналогично, получим . Следовательно, рассматриваемое полукольцо есть булева алгебра.

б. Полукольцо делителей числа 12 не является булевой алгеброй, так как, например, из следует, что , но

Теория булевых алгебр имеет многочисленные приложения: в математической логике, в теории вероятностей. Она позволяет, в частности, рассматривать с единой точки зрения операции над множествами, над высказываниями, над случайными событиями.

Видео:УРАВНЕНИЯ С МОДУЛЕМ | метод интерваловСкачать

Решить булево уравнение примеры с решением

Можно выделить различные способы решения систем логических уравнений. Это сведение к одному уравнению, построение таблицы истинности и декомпозиция.

Задача: Решить систему логических уравнений:

Рассмотрим метод сведения к одному уравнению. Данный метод предполагает преобразование логических уравнений, таким образом, чтобы правые их части были равны истинностному значению (то есть 1). Для этого применяют операцию логического отрицания. Затем, если в уравнениях есть сложные логические операции, заменяем их базовыми: «И», «ИЛИ», «НЕ». Следующим шагом объединяем уравнения в одно, равносильное системе, с помощью логической операции «И». После этого, следует сделать преобразования полученного уравнения на основе законов алгебры логики и получить конкретное решение системы.

Решение 1: Применяем инверсию к обеим частям первого уравнения:

Представим импликацию через базовые операции «ИЛИ», «НЕ»:

Поскольку левые части уравнений равны 1, можно объединить их с помощью операции “И” в одно уравнение, равносильное исходной системе:

Раскрываем первую скобку по закону де Моргана и преобразовываем полученный результат:

Полученное уравнение, имеет одно решение: A =0, B=0 и C=1.

Следующий способ – построение таблиц истинности. Поскольку логические величины имеют только два значения, можно просто перебрать все варианты и найти среди них те, при которых выполняется данная система уравнений. То есть, мы строим одну общую таблицу истинности для всех уравнений системы и находим строку с нужными значениями.

Решение 2: Составим таблицу истинности для системы:

Полужирным выделена строчка, для которой выполняются условия задачи. Таким образом, A=0, B=0 и C=1.

Способ декомпозиции. Идея состоит в том, чтобы зафиксировать значение одной из переменных (положить ее равной 0 или 1) и за счет этого упростить уравнения. Затем можно зафиксировать значение второй переменной и т.д.

Решение 3: Пусть A = 0, тогда:

Из первого уравнения получаем B =0, а из второго – С=1. Решение системы: A = 0, B = 0 и C = 1.

В ЕГЭ по информатике очень часто требуется определить количество решений системы логических уравнений, без нахождения самих решений, для этого тоже существуют определенные методы. Основной способ нахождения количества решений системы логических уравнений – замена переменных . Сначала необходимо максимально упростить каждое из уравнений на основе законов алгебры логики, а затем заменить сложные части уравнений новыми переменными и определить количество решений новой системы. Далее вернуться к замене и определить для нее количество решений.

Задача: Сколько решений имеет уравнение ( A → B ) + ( C → D ) = 1? Где A, B, C, D – логические переменные.

Решение: Введем новые переменные: X = A → B и Y = C → D . С учетом новых переменных уравнение запишется в виде: X + Y = 1.

Дизъюнкция верна в трех случаях: (0;1), (1;0) и (1;1), при этом X и Y является импликацией, то есть является истинной в трех случаях и ложной – в одном. Поэтому случай (0;1) будет соответствовать трем возможным сочетаниям параметров. Случай (1;1) – будет соответствовать девяти возможным сочетаниям параметров исходного уравнения. Значит, всего возможных решений данного уравнения 3+9=15.

Следующий способ определения количества решений системы логических уравнений – бинарное дерево. Рассмотрим данный метод на примере.

Задача: Сколько различных решений имеет система логических уравнений:

Приведенная система уравнений равносильна уравнению:

Предположим, что x ₁ – истинно, тогда из первого уравнения получаем, что x ₂ также истинно, из второго — x ₃=1, и так далее до x_m = 1. Значит набор (1; 1; …; 1) из m единиц является решением системы. Пусть теперь x ₁=0, тогда из первого уравнения имеем x ₂ =0 или x ₂ =1.

Когда x ₂ истинно получаем, что остальные переменные также истинны, то есть набор (0; 1; …; 1) является решением системы. При x ₂=0 получаем, что x ₃=0 или x ₃=, и так далее. Продолжая до последней переменной, получаем, что решениями уравнения являются следующие наборы переменных ( m +1 решение, в каждом решении по m значений переменных):

Такой подход хорошо иллюстрируется с помощью построения бинарного дерева. Количество возможных решений – количество различных ветвей построенного дерева. Легко заметить, что оно равно m +1.