Здесь Вы найдете задач по теме Дисперсные системы и Коллоидные растворы. Это задачи на строение коллоидных частиц (составление формулы мицеллы золя) и коагуляция золей.
Задача 1. Какой объем 0,001 н. раствора BaCl2 надо добавить к 0,03 л 0,001 н. раствора K2CrO4, чтобы получить положительно заряженные частицы золя BaCrO4? Составьте формулу мицеллы золя. Какой из перечисленных электролитов будет обладать более сильным коагулирующим действием: хлорид калия, сульфат калия или фосфат калия. Поясните выбор.
Решение.
Запишем уравнение реакции, протекающей при сливании двух растворов:
BaCl2 + K2CrO4 = BaCrO4↓ + 2KCl
Найдем необходимый объем BaCl2 при условии, что вещества участвуют в реакции в стехиометрическом соотношении, используя «золотое правило аналитики»:
Подставим в выражение известные значения:
0,001·0,03 = 0,001·VBaCl2, откуда
На поверхности образовавшегося золя адсорбируются ионы, входящие в его состав и находящиеся в растворе в избытке.
Чтобы получить «+» заряженные частицы золя BaCrO4, на его поверхности должны адсорбироваться ионы Ba 2+ . Таким образом, в растворе должен быть избыток BaCl2 по сравнению с K2CrO4, т.е. к 0,03 л 0,001 н. раствора K2CrO4 необходимо добавить более 0,03 л. 0,001 н. раствора BaCl2.
Т.к. частицы золя заряжены положительно, то к ним будут притягиваться отрицательно заряженные ионы Cl — .
Формула мицеллы золя будет выглядеть следующим образом:
[(BaCrO4)m·nBa 2+ , 2(n-x)Cl — ] 2x+ ·2xCl —
Какой из перечисленных электролитов будет обладать более сильным коагулирующим действием: хлорид калия, сульфат калия или фосфат калия. Поясните выбор.
Коагуляцию золя вызывает тот из ионов добавляемого электролита, чей заряд противоположен заряду коллоидной частицы. Коагулирующая способность иона тем больше, чем больше его заряд.
Допустим, что коагуляцию золя вызывают катионы, тогда все приведенные соединения обладают одинаковым коагулирующим действием.
Если же коагуляция золя вызвана анионами, то более сильным коагулирующим действием будет обладать фосфат калия K3PO4, т.к. фосфат-ион имеет наибольший заряд.
Задача 2. Золь Al(OH)3 получен при добавлении к 0,005 л 0,001 н. раствора AlCl3 0,002 л 0,0015 н. раствора NaOH. Напишите формулу мицеллы золя. Какой из перечисленных электролитов будет обладать более сильным коагулирующим действием: нитрат калия, сульфат магния или фосфат калия. Поясните выбор.
Решение.
Запишем уравнение реакции, протекающей при сливании двух растворов:
Определим количества участвующих в реакции веществ:
n(NaOH)= Сн·V = 0,0015·0,002 = 3·10 -6 моль
Следовательно, в избытке AlCl3, значит, ядром коллоидных частиц будут адсорбироваться Al 3+ и частицы золя приобретут положительный заряд. Противоионами будут служить ионы Cl — .
Формула мицеллы золя будет выглядеть следующим образом:
[(Al(OH)3)m·nAl 3+ , 3(n-x)Cl — ] 3x+ ·3xCl —
Какой из перечисленных электролитов будет обладать более сильным коагулирующим действием: нитрат калия, сульфат магния или фосфат калия. Поясните выбор.
Коагуляцию золя вызывает тот из ионов добавляемого электролита, чей заряд противоположен заряду коллоидной частицы. Коагулирующая способность иона тем больше, чем больше его заряд.
Допустим, что коагуляцию золя вызывают катионы, тогда наиболее сильным коагулирующим действием будет обладать сульфат магия MgSO4, т.к заряд иона магния имеет наибольшее значение.
Если же коагуляция золя вызвана анионами, то более сильным коагулирующим действием будет обладать фосфат калия K3PO4, т.к. фосфат-ион имеет наибольший заряд.
Задача 3. Какой объем 0,0025 н. раствора KI надо добавить к 0,035 л 0,003 н. раствора Pb(NO3)2, чтобы получить золь PbI2, противоионы которого двигались бы в электрическом поле к аноду? Напишите формулу мицеллы золя. Какой из перечисленных электролитов будет обладать более сильным коагулирующим действием: хлорид натрия, сульфат натрия или фосфат калия. Поясните выбор.
Решение.
Запишем уравнение реакции, протекающей при сливании двух растворов:
2KI + Pb(NO3)2 = PbI2↓+ 2KNO3
При образовании золя PbI2, на его поверхности адсорбируются потенциалопределяющие ионы, входящие в его состав и находящиеся в растворе в избытке.
Далее, к ядру притягиваются противоположно заряженные ионы – противоионы, которые компенсируют заряд твердой фазы и образуют адсорбционный слой. Противоионами будут служить, ионы, содержащиеся в растворе, но не входящие в состав агрегата.
По условию задачи, противоионы движутся к аноду, значит, они заряжены отрицательно, а потенциалопределяющие ионы будут заряжены положительно. В нашем примере, в качестве потенциалопределяющих ионов будут выступать ионы свинца. В результате, (PbI2)m с адсорбированным слоем Pb 2+ приобретает положительный заряд. Противоионами служат нитрат-ионы NO3 – .
Таким образом, в растворе должен быть избыток Pb(NO3)2.
Применяя «золотое правило аналитики», найдем объем KI:
Подставим в выражение известные значения:
0,0025·VKI = 0,003·0,035, откуда
Следовательно, чтобы достичь избытка Pb(NO3)2, объем VKI должен быть менее 0,042 л.
Формула мицеллы золя будет выглядеть следующим образом:
Какой из перечисленных электролитов будет обладать более сильным коагулирующим действием: хлорид натрия, сульфат натрия или фосфат калия. Поясните выбор.
Коагуляцию золя вызывает тот из ионов добавляемого электролита, чей заряд противоположен заряду коллоидной частицы. Коагулирующая способность иона тем больше, чем больше его заряд.
Допустим, что коагуляцию золя вызывают катионы, тогда все приведенные соединения обладают одинаковым коагулирующим действием, т.к. все катионы имеют положительный заряд.
Если же коагуляция золя вызвана анионами, то более сильным коагулирующим действием будет обладать фосфат калия K3PO4, т.к. фосфат-ион имеет наибольший заряд.
Задача 4. Золь Mg3(РО4)2 получен при добавлении к 0,015 л 0,002 н. раствора Na3PO4 0,005 л 0,004 н. раствора MgCl2. Укажите формулу мицеллы золя. Какой из перечисленных электролитов будет обладать более сильным коагулирующим действием: хлорид калия, сульфат меди или нитрат алюминия. Поясните выбор.
Решение.
Запишем уравнение реакции, протекающей при сливании двух растворов:
Определим количества участвующих в реакции веществ:
n(MgCl2)= Сн·V = 0,004·0,005 = 0,00002 моль
Как видно из расчетов, в избытке Na3PO4, значит, в качестве потенциалопределяющих ионы, т.е. ионов, входящие в его состав и находящиеся в растворе в избытке, выступают PO4 3- .
Далее, к ядру притягиваются противоположно заряженные ионы – противоионы, которые компенсируют заряд твердой фазы и образуют адсорбционный слой. Противоионами будут служить, ионы, содержащиеся в растворе, но не входящие в состав агрегата – Na +
Формула мицеллы золя будет выглядеть следующим образом:
Какой из перечисленных электролитов будет обладать более сильным коагулирующим действием: хлорид калия, сульфат меди или нитрат алюминия. Поясните выбор.
Коагуляцию золя вызывает тот из ионов добавляемого электролита, чей заряд противоположен заряду коллоидной частицы. Коагулирующая способность иона тем больше, чем больше его заряд.
K + Cl — , Cu 2+ SO4 2- , Al 3+ (NO3)3 —
Допустим, что коагуляцию золя вызывают катионы, тогда наибольшим коагулирующим действием обладает нитрат алюминия Al(NO3)3, т.к. ион Al 3+ имеет наибольший заряд.
Если же коагуляция золя вызвана анионами, то более сильным коагулирующим действием будет обладать сульфат меди CuSO4, т.к. сульфат-ион имеет наибольший заряд.
Задача 5. Золь Zn(OH)2 получен при взаимодействии растворов КОН и ZnCl2. Составьте формулу мицеллы золя, если противоионы движутся в электрическом поле к катоду. Какой из перечисленных электролитов будет обладать более сильным коагулирующим действием: ацетат калия, сульфат никеля или сульфат хрома. Поясните выбор.
Решение.
Запишем уравнение реакции, протекающей при сливании двух растворов:
2KOH + ZnCl2 = Zn(OH)2↓+ 2KCl
При образовании золя Zn(OH)2, на его поверхности адсорбируются потенциалопределяющие ионы, входящие в его состав и находящиеся в растворе в избытке.
Далее, к ядру притягиваются противоположно заряженные ионы – противоионы, которые компенсируют заряд твердой фазы и образуют адсорбционный слой. Противоионами будут служить, ионы, содержащиеся в растворе, но не входящие в состав агрегата.
По условию задачи, противоионы движутся к катоду, значит, они заряжены положительно, а потенциалопределяющие ионы будут заряжены отрицательно.
В нашем примере, в качестве потенциалопределяющих ионов будут выступать гидроксид-ионы. В результате, (Zn(OH)2)m с адсорбированным слоем OH — приобретает отрицательный заряд.
Противоионами служат ионы K + .
Формула мицеллы золя будет выглядеть следующим образом:
Какой из перечисленных электролитов будет обладать более сильным коагулирующим действием: ацетат калия, сульфат никеля или сульфат хрома. Поясните выбор.
Коагуляцию золя вызывает тот из ионов добавляемого электролита, чей заряд противоположен заряду коллоидной частицы. Коагулирующая способность иона тем больше, чем больше его заряд.
Допустим, что коагуляцию золя вызывают анионы, тогда наибольшим коагулирующим действием обладают сульфат никеля NiSO4 и сульфат хрома Cr2(SO4)3.
Если же коагуляция золя вызвана катионами, то более сильным коагулирующим действием будет обладать сульфат хрома Cr2(SO4)3, т.к. ион хрома имеет наибольший заряд.
Задача 6. Золь Ag2S получен при добавлении к 0,015 л 0,003 н. раствора Na2S 0,035л 0,0005 н. раствора AgNO3. Напишите формулу мицеллы золя. Какой из перечисленных электролитов будет обладать более сильным коагулирующим действием: хлорид калия, сульфат цинка или фосфат калия. Поясните выбор.
Решение.
Запишем уравнение реакции, протекающей при сливании двух растворов:
Определим количества участвующих в реакции веществ:
n(Na2S)= Сн·V = 0,003·0,015 = 0,000045 моль
n(AgNO3)= Сн·V = 0,0005·0,035 = 0,0000175 моль
Как видно из расчетов, в избытке находится Na2S, значит, в качестве потенциалопределяющих ионы, т.е. ионов, входящие в его состав и находящиеся в растворе в избытке, выступают S 2- .
Далее, к ядру притягиваются противоположно заряженные ионы – противоионы, которые компенсируют заряд твердой фазы и образуют адсорбционный слой.
Противоионами будут служить, ионы, содержащиеся в растворе, но не входящие в состав агрегата – Na +
Формула мицеллы золя будет выглядеть следующим образом:
[(Ag2S)m·nS 2- , 2(n-x)Na + ] 2x- ·2xNa +
Какой из перечисленных электролитов будет обладать более сильным коагулирующим действием: хлорид калия, сульфат цинка или фосфат калия. Поясните выбор.
Коагуляцию золя вызывает тот из ионов добавляемого электролита, чей заряд противоположен заряду коллоидной частицы. Коагулирующая способность иона тем больше, чем больше его заряд.
K + Cl — , Zn 2+ SO4 2- , K3 + (PO4) 3-
Допустим, что коагуляцию золя вызывают анионы, тогда наибольшим коагулирующим действием обладают фосфат калия K3PO4, т.к. фосфат-ион PO4 3- имеет наибольший заряд.
Если же коагуляция золя вызвана катионами, то более сильным коагулирующим действием будет обладать сульфат цинка ZnSO4, т.к. ион цинка Zn 2+ имеет наибольший заряд.
Задача 7. Золь Fe(OH)3 получен смешиванием равных объемов 0,0001 н. раствора KOH и 0,00015 н. раствора FeCl3. Укажите формулу мицеллы золя. Какой из перечисленных электролитов будет обладать более сильным коагулирующим действием: нитрат свинца, сульфат марганца или фосфат калия. Поясните выбор.
Решение.
Запишем уравнение реакции, протекающей при сливании двух растворов:
3KOH + FeCl3 = Fe(OH)3↓+ 3KCl
По условию задачи объемы смешиваемых растворов равны, поэтому в избытке будет находиться вещество с наибольшей концентрацией, т.е. хлорид железа FeCl3.
Таким образом, в качестве потенциалопределяющих ионы, т.е. ионов, входящих в состав ядра и находящиеся в растворе в избытке, выступают Fe 3+ .
Далее, к ядру притягиваются противоположно заряженные ионы – противоионы, которые компенсируют заряд твердой фазы и образуют адсорбционный слой.
Противоионами будут служить, ионы, содержащиеся в растворе, но не входящие в состав агрегата – Cl — .
Формула мицеллы золя будет выглядеть следующим образом:
[(Fe(OH)3)m·nFe 3+ , 3(n-x)Cl — ] 3x+ ·3xCl —
Какой из перечисленных электролитов будет обладать более сильным коагулирующим действием: нитрат свинца, сульфат марганца или фосфат калия. Поясните выбор.
Коагуляцию золя вызывает тот из ионов добавляемого электролита, чей заряд противоположен заряду коллоидной частицы. По правилу Шульца-Гарди коагулирующая способность иона тем больше, чем больше его заряд.
Pb 2+ (NO3)2 — , Мn 2+ SO4 2- , K3 + (PO4) 3-
Допустим, что коагуляцию золя вызывают анионы, тогда наибольшим коагулирующим действием обладают фосфат калия K3PO4, т.к. фосфат-ион PO4 3- имеет наибольший заряд.
Если же коагуляция золя вызвана катионами, то более сильным коагулирующим действием будут обладать нитрат свинца Pb(NO3)2и сульфат марганца МnSO4, т.к. ионы свинца Pb 2+ и марганца Мn 2+ имеют наибольший заряд, по сравнению с ионом K +
Видео:Решение задач на термохимические уравнения. 8 класс.Скачать

По физической и коллоидной химии
Пятигорская государственная фармацевтическая академия
Кафедра физической и коллоидной химии
Примеры задач с решениями
по физической и коллоидной химии
Для студентов II и III курсов
Авторы: доц. Л.П. Мыкоц, ст. преп. А.В. Погребняк, ст. преп. Е.И. Распопов
асс. С.Н.Бондарь, асс. Т.А.Савельева, асс. Т.Н.Сысоева,
Под общей редакцией
заведующего кафедрой физической и коллоидной химии,
доцента Л.П. Мыкоц
Рецензент: зав. кафедрой неорганической химии, профессор,
д.ф.н. В.А. Компанцев.
Утверждено на заседании ЦМС ПГФА «____»__________________2005 г.
Председатель ЦМС профессор Погорелов В.И.
Сборник типовых задач с решениями по физической и коллоидной химии для студентов 2,3 курсов очного и заочного отделений подготовлен на кафедре физической и коллоидной химии в соответствии с программой по дисциплине: физическая и коллоидная химия, Москва, 2002 год. Рекомендовано ЦМС ПГФА для подготовки студентов к сдаче экзамена и для выполнения контрольных работ студентов заочного отделения внутри академии
Предисловие
Навык решения задач является одной из самых важных составляющих образовательного процесса в разделе естественно-научных дисциплин. Решая задачи, студенты приобретают знания, необходимые для использования теории в практических целях. С учетом роста требований к практическим знаниям выпускников фармацевтических вузов и факультетов, обучение их методам и приемам расчетов выходит на первый план.
Настоящее пособие, не подменяя существующие учебники и сборники задач, предоставляет студентам фармацевтических факультетов очного и заочного отделений возможность достаточно быстро освоить приемы решения важнейших задач, включенных в действующую Учебную программу по физической и коллоидной химии, а также успешно подготовиться к заключительному экзамену.
В настоящий сборник задач по физической и коллоидной химии, подготовленный коллективом преподавателей кафедры физической и коллоидной химии Пятигорской ГФА вошли примеры решения типовых задач, в том числе:
по разделам физической химии — основы химической термодинамики, фазовые равновесия, электрохимия, кинетика химических реакций;
по разделам коллоидной химии — поверхностные явления, дисперсные системы, высокомолекулярные вещества.
Примеры решения задач по физической химии
Задача 1. Вычислите DН о , DU о , DG о и DА 0 для реакции
Определите, возможно ли самопроизвольное протекание реакции при стандартных условиях.
Решение: Воспользовавшись данными, приведенными в Приложении, рассчитаем тепловой эффект реакции при постоянном давлении:
= 2DН o f CO + DН o f O2 – 2DН o f CO2 =
= [2(–110,70) + 0] – 2(–393,51) = 565,62 кДж/моль.
Изменение внутренней энергии связано с изменением энтальпии зависимостью: DU o r = DH o r – DnRT,
где: Dn – изменение числа молей газообразных веществ в ходе реакции,
R – универсальная газовая постоянная (8,314´10 — 3 кДж/моль·К);
DU 0 r = 565,62 – 8,314´10 –3 ·298 = 563,14 кДж/моль.
Для расчета DG o r найдем предварительно изменение энтропии:
= (2´197,48+205,03) – 2´213,66 = 172,67 Дж/моль·К.
Tогда изменение энергии Гиббса будет равно:
DG о r = DН о r – ТDS 0 r = 565,62 – 298·172,67´10 –3 = 514,16 кДж/моль.
Теперь определим изменение энергии Гельмгольца:
DА o r = DU o r – TDS o r = 563,14–298·172,67´10 –3 = 511,68 кДж/моль
Положительные значения величин DG o r и DА o r указывают на то, что при стандартных условиях реакция не будет самопроизвольно идти в прямом направлении.
Задача 2. Для реакции крекинга метана
Используя данные Приложения, рассчитать ΔG 0 r298 и ΔA 0 r298. Определить,
возможно ли самопроизвольное протекание данной реакции при температуре
1) Воспользовавшись данными Приложения
рассчитаем ΔG 0 r (изменение энергии Гиббса)
= 0 + 2× 0 – (-50,85) = +50,85 кДж
2) Для расчета ΔA 0 r воспользуемся соотношением между ΔG 0 r и ΔA 0 r:
где Δn – изменение числа молей газообразных веществ в ходе реакции,
R — универсальная газовая постоянная
Находим Δn: Δn = ånпрод. — ånисх. = 2 – 1 = 1
ΔA 0 r = 50,89 — 1× 8,314 × 10 -3 × 298 = 48,41 кДж,
т.к. ΔG 0 r298 и ΔA 0 r298 > 0, то при 298 К невозможно самопроизвольное протекание данной реакции в прямом направлении.
Задача 3. Для реакции крекинга метана
Рассчитать ΔН 0 r, используя значение стандартных теплот сгорания веществ (лДж/моль): ΔН 0 с СН4 (г) = — 890,31; ΔН 0 с С (т) = -393,51; ΔН 0 с Н2 (г) = -285,84
Определить экзо- или эндотермической является данная реакция.
Решение: В соответствии со следствием закона Гесса:
= ΔН 0 с СН4 (г) – (ΔН 0 с С (т) + 2 ΔН 0 с Н2 (г)) =
= -890,31 — [-393,51 + 2× (-285,84)] = +74,88 кДж
т.к. ΔН 0 r > 0, реакция является эндотермической.
Задача 4. Напишите уравнение реакции сгорания метана.Вычислите стандартную теплоту образования метана, если его стандартная теплота сгорания
ΔН 0 с = -890,31 кДж/моль
Продукты сгорания имеют следующие теплоты образования (кДЖ/моль)
Напишите термохимическое уравнение реакции сгорания метана
В соответствии со следствием закона Гесса:
С другой стороны: ΔН 0 r = ΔН 0 С СН4 (г)
-890,31 = (-393,51 + 2× (-285,84) ) – (ΔН 0 f СН4 (г) + 2 × 0);
— 890,31 = -393,51 – 571,68 — ΔН 0 f СН4 (г)
Задача 5. Используя уравнение Кирхгоффа для небольшого температурного интервала рассчитать тепловой эффект реакции
при температуре 500К и давлении 1,0133´10 5 Па.
Решение: По данным приложения сначала рассчитываем тепловой эффект реакции при 298К:
= (–393,51–2´241,8) –(–201,00 + 3/2´0) = –676,13 кДж/моль.
Зная DН о r 298, можно по уравнению Кирхгоффа рассчитать тепловой эффект реакции при 500К:
где DС о р – изменение теплоемкости в ходе реакции. Его можно определить таким образом:
= (37,11+2´33,56)–(43,9–3/2´28,83) = 17,10 Дж/моль•К
и значит, тепловой эффект реакции при 500К равен:
= –676130 + 17,1´202 = –672676 Дж/моль = –672,676 кДж/моль.
Задача 6. Значение стандартной энергии Гиббса DG o r реакции
равно –3,434 кДж/моль. Вычислите константы равновесия Кр и Кс. Каков будет состав равновесной реакционной смеси, если в реакцию введены 1 моль кислоты и 2 моля спирта?
Решение: Воспользуемся соотношением DG o r = – RTlnKp, из которого получаем
RT 8,314х10 -3 х298
и значит Кр = е 1,386 = 3,9989 » 4.
Кс = Кр(RT) – D n , а так как Dn = 2 – 2 = 0, то Кс = Кр = 4.
Для того, чтобы ответить на вопрос о составе равновесной реакционной смеси, необходимо в общем виде проанализировать начальный и равновесный состав реакционной смеси:
Выразим константу равновесия через равновесные количества молей веществ:
и решим уравнение относительно х:
х 2 =(1-х)(2-х)= 4; х 2 =(2–3х+х 2 )= 4; х 2 =8–12х+4х 2 ; 3х 2 –12х+8=0

12 + 6,928 12 – 6,928
значение = 3,15 мол. х1 не имеет физического смысла (так как из 2 молей спирта нельзя получить 3 моля этилацетата) и отбрасывается. Таким образом, состав реакционной смеси при равновесии будет следующим:
уксусной кислоты: 1–0,845 = 0,155 моля,
спирта: 2–0,845 = 1,155 моля,
этилацетата: 0,845 моля,
Задача 7. Выразите известным вам способом концентрацию раствора 10 г NaCl в 100 мл (г) воды. В качестве способов выражения концентрации используйте:
1) молярную весовую концентрацию (моляльность);
2) молярную объемную концентрацию (молярность);
3) нормальность (молярную концентрацию эквивалента) ;
4) моляльную (молярную) долю;
6) весовой процент;
7) число граммов растворенного вещества на 100 г растворителя (коэффициент растворимости при данных условиях).
Э — эквивалентный вес растворённого вещества; nNaCl • m’H2O (1000 г) 0.17 • 1000 nNaCl • 1000 мл 0.17 1000 100 мл (V H2O) 100 также возможен расчет нормальности раствора по следующей формуле: m – масса, г; X — массовая доля, %; Э — эквивалентная масса, г/г-экв. Задача 8. В 100 г воды растворено 1,53 г глицерина. Давление пара воды при 298К равно 3167,2 Н/м 2 . Вычислите: а) понижение давления пара воды над раствором; б) температуру кипения раствора; в) температуру его замерзания; г) его осмотическое давление. а) В соответствии с законом Рауля относительное понижение давления равновесного с раствором пара равно: где Хгл – мольная доля глицерина в растворе. nводы=100/18 = 5,555 моль; nгл = 1,53/92 = 0,017 моль; Значит, Хгл= 0,017/(0,017 + 5,555) = 0,003, и тогда Dр/3167,2 = 0,03; DР = 95,02 Па. б) Повышение температуры кипения раствора неэлектролита можно вычислить по эбуллиоскопической формуле: где Кэ – эбуллиоскопическая константа растворителя (для воды она равна 0,52); m – масса растворенного вещества в граммах; М – его молярная масса; а – масса растворителя в граммах. Отсюда Следовательно, температура кипения раствора будет равна 100,086 0 С. в) Понижение (депрессия) температуры замерзания раствора рассчитывается по криоскопической формуле: где Кк — криоскопическая константа растворителя (для воды 1,86): Следовательно, раствор будет замерзать при –0,309 о С. г) в соответствии с законом Вант–Гоффа осмотическое давление в растворах неэлектролитов можно рассчитать по уравнению где С – молярная концентрация раствора. При пересчете в систему СИ концентрация должна быть выражена в моль/м 3 . Считая плотность раствора равной плотности воды, получим: С = ¾¾¾¾¾ = 0,17 моль/л = 0,17´10 3 моль/м 3 . p = 0,17´10 3 ·8,314·298 = 421187,2 Па (» 4,2 атм). Рассчитайте осмотическое давление водного раствора хлорида кальция с концентрацией 0,05 моль/л при температуре 37 0 С. Степень диссоциации (ионизации) CaCl2 равна 97%. Каким этот раствор является по отношению к плазме крови: гипо-, гипер- или изотоническим ? Осмотическое давление растворов электролитов рассчитывается по уравнению Вант — Гоффа: где i — изотонический коэффициент Вант – Гоффа С – концетрация раствора ( моль/л, моль/м 3 ) R – универсальная газовая постоянная Т – температура, К Расчет i: i = 1 + a(n — 1), где a — кажущаяся степень диссоциации электорлита n — число частиц (ионов), на который диссоциирует молекула электролита СаСl2 « Са 2+ + 2Сl — (n = 3); i = 1 + 0,97(3 – 1) = 1 + 1,94 = 2,94 pосм = iCRT = 2,94 × 0,05 × 0,082 × 310 = 3,74 атм. или: pосм = 2,94 × 0,05 × 10 3 × 8,314 × 310 = 378868,98 p а где n — число операций экстрагирования. в) Перейдет в экстракт при четырехкратном экстрагировании mэ = m0 — m = 1 — 0,00044 = 0,99956 г. m = m0 [1– ¾¾¾¾ ] = 1· [1 — ¾¾¾¾¾¾¾ ] = 0,99956 г г) Степень извлечения вычислим как отношение массы иода, перешедшего в экстракт, к массе его в исходном водном растворе. В первом случае: a1 = (1–0,041)/1 = 0,959 или 95%; во втором случае: a2 = 0,99956/1 = 0,99956 или 99,956%. д) Число экстракций для достижения заданной степени извлечения при V2=10 мл, найдем с помощью уравнения, использованного в п. (в): a = mэ/m0 = 1 – (¾¾¾¾) ; 0,97 = 1 – 0,145 n ; 0,03 = 0,145 n . lg 0,03 = n lg 0,145; n = lg 0,03/lg 0,145 = (-1,5229/-0,8386) =1,82. Т.е. число экстракций равно двум (1,82»2). Задача 11. Вычислить давление, необходимое для понижения температуры замерзания воды на 1 о , и температуру, при которой будет плавиться лед при повышении давления на 1 атм. При 0 о С удельная теплота плавления льда равна 333,5´10 3 Дж/кг, плотность воды 0,9998´10 3 кг/м 3 , плотность льда 0,9168´10 3 кг/м 3 . Решение: Используем уравнение Клапейрона для фазовых превращений в однокомпонентных системах: где Dр/DТ – изменение давления фазового превращения при изменении температуры на 1 градус; L – удельная теплота фазового превращения при температуре Т; DV = (Vж – Vтв) – изменение удельного объема при фазовом переходе. Удельные объемы – величины обратные плотности, следовательно: Vж=1/9,998´10 2 =1,0002´10 –3 м 3 /кг; Vтв=1/9,168´10 2 =1,0908´10 –3 м 3 /кг; и DV=1,0002´10 –3 – 1,0908´10 –3 = –9,06´10 –5 м 3 /кг; Знак «минус» указывает на то, что для уменьшения температуры кристаллизации воды (или плавления льда) давление должно быть повышено. Следовательно, для понижения температуры замерзания воды на 1 о С необходимо давление повысить на 134,8´10 5 Па (или 133 атм), т.е. довести его до 134 атм. Изменение температуры фазового перехода при изменении давления на единицу найдем с помощью преобразования уравнения: или ¾¾ = ¾¾¾ = –0,0075 К/атм; Следовательно, при повышении давления на 1 атм температура плавления льда уменьшается на 0,0075К и становится равной -0,0075 о С. Задача 12. Рассчитайте количество водяного пара, необходимого для перегонки 10 кг анилина, если смесь анилина с водой при атмосферном давлении кипит при 98,4 о С. При этой температуре давление водяного пара равно 94605 Па. Решение. Коэффициент расхода пара mв/mа при перегонке с водяным паром рассчитывается по уравнению: где mв и mа –массы воды и анилина, Мв и Ма – молярные массы воды и анилина; рв и ра – парциальные давления паров воды и анилина при температуре перегонки. ра находится с помощью закона Дальтона как разность между нормальным атмосферным давлением и рв: ра = 101325 Па – 94605 Па = 6720 Па. Следовательно, для перегонки 1 кг анилина требуется 2,72 кг водяного пара, а для 10 кг анилина его понадобится 27,2 кг. Задача 13 . Раствор, содержащий 0,8718 моль/л тростникового сахара, при Т = 291К, изотоничен с раствором хлорида натрия, содержащим 0,5 моль/л NaCl.Рассчитайте: а) изотонический и осмотический коэффициенты для хлорида натрия; б) кажущуюся степень его диссоциации. а) Для раствора сахара осмотическое давление рассчитывается по уравнению Вант-Гоффа для неэлектролитов: p1 = С1RT; а для раствора NaCl по уравнению для электролитов: p2 = iC2RT, где i -изотонический коэффициент. Так как осмотические давления растворов равны, т.е. p1 = p2, и значит С1RT = iC2RT. По величине изотонического коэффициента рассчитываем осмотический коэффициент g: g = i/n = 1,7436/2 = 0,8718, где n– число ионов, образующихся при диссоциации одной молекулы. б) Кажущуюся степень диссоциации a вычисляем с помощью уравнения, связавющего ее с изотоническим коэффициентом: Отсюда a = (i –1)/(n–1) = (1,7436 –1)/(2 –1) = 0,7436. Задача 14. Для предотвращения частичного разложения лекарственного препарата в кипящем водном растворе при отгонке воды необходимо понизить температуру кипения на 20 о . Вычислите, какое давление при этом надо поддерживать в перегонном аппарате. Теплота испарения воды Решение: Используем для расчета уравнение Клапейрона–Клаузиуса: Считая, что температура кипения раствора T2 при нормальном атмосферном давлении р2 = 101325 Па равна 100 о С (373К), подставим значения: 101325 40660 (373 – 353) отсюда lnр1 = ln101325 – 0,7428 = 11,5261 – 0,7428 = 10,7832, и значит, требуемое давление р1 = e 10,7832 = 48204 Па (0,47 атм.). Задача 15. Рассчитайте объемы 0,1 М растворов уксусной кислоты и ацетата натрия, необходимые для приготовления 20 мл ацетатного буферного раствора с рН = 4. Решение. Так как концентрации растворов одинаковы, расчет ведется по уравнению: где рКа – показатель кислотности уксусной кислоты, равный 4,74; Vс.о. и Vс.к. – соответственно объемы растворов сопряженных основания и кислоты. Отсюда при Сс.к. = Сс.о. : откуда объем раствора уксусной кислоты Vс.к. = 16,95 мл, и объем раствора ацетата натрия Vс.о. = 20 – 16,95 = 3,05 мл. Задача 16. Удельная электрическая проводимость 0,175 М раствора аммиака равна 4,76´10 –4 Ом –1 см –1 . Подвижность ионов NH4 + и ОН – при 25 о С соответственно равны 73,5 и 198,3 Ом –1 см 2 моль –1 . Рассчитайте молярную проводимость, степень и константу ионизации аммиака, его рКb, концентрацию ионов водорода в растворе и его рН. Решение: Удельная À и молярная l электрические проводимости связаны между собой соотношением где С – концентрация в моль/л, 1000 – пересчетный коэффициент из литров в см 3 . l = ¾¾¾¾¾¾¾ = 2,72 Ом –1 см 2 моль –1 Степень ионизации a можно вычислить с помощью отношения a=l/l¥ , где l¥ – молярная проводимость при бесконечном разведении, которая рассчитывается по закону Кольрауша: l¥ = l+ + l– (l+ и l– – подвижности ионов): l¥ = 73,5 + 198,3 = 271,8 Ом –1 см 2 моль –1 Отсюда a = 2,72/271,8 = 0,01. В соответствии с законом разведения Оствальда К = a 2 С/(1–a), где К – константа ионизации электролита (в данном случае К = Кb С – концентрация, выраженная в моль/л. Концентрация ионов ОН – в растворе будет равна aС: СОН– = 0,01·0,175 = 0,00175 моль/л. Отсюда рОН = – lg0,00175 = 2,76 и, значит, pH = 14 – 2,76 = 11,24. Задача 17. Написать формулу гальванического элемента, состоящего из медного электрода, погруженного в раствор сульфата меди с активностью 0,01 М и цинкового электрода, погруженного в раствор хлорида цинка с активностью 0,02 М. Решение: Опорным при составлении формулы гальванического элемента является электрохимический ряд напряжений металлов, приведенный ниже: Электрохимический ряд напряжений металлов Li K Ba Ca Na Mg Al Mn Cr Zn Fe Co Sn Pb H2 Cu Hg Ag Au Ослабление восстановительных свойств (активности) слева направо Формула начинается со знака минус в круглых скобках, затем указывается металл, находящийся слева в ряду напряжений, в нулевой степени окисления. Ставится вертикальная черта, имеющая значение границы раздела между металлом и ионосодержащим раствором. За ней указывается активный ион. Далее следует вертикальная двойная черта, обозначающая границу между двумя полуэлементами и показывающая, чо диффузный потенциал устранен. За двойной чертой (в зеркальном порядке) указывается активный ион второго полуэлемента и, через одинарную вертикальную черту, металл в нулевой степени окисления, находящийся в электрохимическом ряду справа. За ним следует знак «плюс» в круглых скобках. Под каждым из активных ионов подписывается соответствующая ему активность из условия задачи. Конечный результат должен выглядеть следующим образом: (-) Zn 0 | Zn 2+ || Cu 2+ | Cu 0 (+) М 0,01М Примечание: вместо активного иона позволительно указывать также и полную брутто формулу соли, в раствор которой погружен соответствующий электрод. Задача 18. Рассчитайте электродные потенциалы, ЭДС гальванического элемента (–)Zn|ZnSO4 (c=0,5M)||CuSO4 (c=1M)|Cu(+), изменение энергии Гиббса DG о и константу равновесия реакции, протекающей в нем при замыкании цепи (Т=25 0 С). Решение: Потенциалы электродов вычислим с помощью уравнения Нернста: где Е о Ме n + /Ме – стандартный электродный потенциал (см. Приложение); aМе n + – активность соответствующих ионов в растворе; n – число электронов, участвующих в электродной реакции; F – число Фарадея (96500 Кл). Для расчета активности а = gС находим в справочнике коэффициенты активности g солей и подставляем их значения: ЕZn 2+ /Zn = –0,763 + (0,059/2) lg 0,0315 = –0,807 В. И, значит, электродвижущая сила равна Между DG 0 реакции, протекающей в гальваническом элементе, и стандартной ЭДС существует связь, выражаемая уравнением: DG о = –nFE о . Стандартная ЭДС рассчитывается как разность стандартных электродных потенциалов: Е о = Е о + – Е о – . Значит Е о = +0,337 –(–0,763) = 1,100 В, и DG о = –2·96500·1,100 = –212300 Дж/моль. Константа равновесия реакции (Ка = Кр) находится с помощью уравнения откуда lnKа = lnKp = – DG 0 /RT = – (–212300)/[8,314·(25+273)] = = 85,6887 и Ка = Кр = е 85,6887 = 1,64´10 37 . Задача 19. Рассчитать растворимость и произведение растворимости сульфида цинка при 25 о С. Электродвижущая сила концентрационного гальванического элемента Zn | ZnS || ZnSO4 | Zn Решение: ЭДС данного концентрационного элемента определяется уравнением: Примем, что aZn 2+ , (1) – концентрация (активность) ионов цинка в насыщенном растворе ZnS, равная х. Тогда aZn 2+ , (2) = gС= 0,063´0,5 = 0,0315 (см. предыдущую задачу). ¾¾¾¾ = 10 9,3559 = 2,2693´10 9 ; и далее: х = aZn 2+ , (1) = 0,0315/(2,2693´10 9 ) = 1,391´10 –11 . Значит, концентрация сульфида цинка в насыщенном растворе равна 1,39´10 –11 моль/л, а его произведение растворимости — ПР = СZn 2+ · CS 2– = х 2 = (1,39´10 –11 ) 2 = 1,93´10 –22 . Задача 20 . Электродвижущая сила Е элемента, составленного из водородного и насыщенного каломельного электродов при 25°С равна 0,4185 В. Чему равны рН раствора, с которым контактирует водородный электрод, и активность ионов водорода в нем? (потенциал каломельного электрода берем из Приложения). Отсюда рН = (0,4185–0,2415)/0,059 = 3 ; аН+ = 10 –рН = 10 –3 = 0,001 моль/л. Задача 21. Константа скорости омыления этилацетата гидроксидом натрия при 10°С равна 2,38 мин –1 . Определить время, необходимое для омыления 90% этилацетата, если реакционная смесь получены смешением 1л 0,05 н. раствора этилацетата с: 1)1 л 0,05 н. раствора NаОН; 2) 1 л 0,1 н. раствора NaОН. 1) Реакция омыления этилацетата в щелочной среде является реакцией второго порядка. В случае равенства концентраций эфира и щелочи воспользуемся уравнением : где а – исходное количество молей; х – количество прореагировавшего вещества к моменту времени t. Общий объем смеси 2 л, поэтому концентрация веществ вследствие разбавления уменьшится в два раза и значит, а = 0,025 моль/л, х = 0,025·0,9 = 0,0225 моль/л. 2. Во втором случае концентрации эфира и щелочи неодинаковы, поэтому необходимо использовать уравнение: Если а — начальная концентрация этилацетата, а b – начальная концентрация щелочи, то а = 0,1/2 = 0,05 моль/л; b = 0,05/2 = 0,025 моль/л; x = 0,025´0,9 = 0,0225 моль/л. Решаем уравнение относительно t2: 2,38 (0,05-0,025) 0,05(0,025–0,0225) Задача 22. Константа скорости диссоциации фосгена при температуре 382 о С равна 0,5´10 –2 мин –1 , а при температуре 482 о С — 67,6´10 –2 мин –1 . Рассчитать: а) энергию активации реакции; б) константу скорости реакции при температуре 425 о С; в) количество фосгена, которое разложится при температуре 382 о С за 100 минут после начала реакции, если начальное содержание его составляло 1 моль/л. а) Расчет энергии активации Е * ведем по уравнению: где: k1 и k2 – константы скорости реакции соответственно при температурах Т1 и Т2. Подставляем значения: 655·755·8,314 67,6´10 –2 Е * = ¾¾¾¾¾¾¾ln¾¾¾¾¾ = 201740,3 Дж/моль » 201,7 кДж/моль б) Для расчета константы скорости реакции при 425 о С воспользуемся тем же уравнением и найденным значением Е * . Решая это уравнение относительно k3, получим: ln k3 = ¾¾¾¾ · ¾¾¾¾¾ + ln 0,5´10 –2 = –3,016, откуда k3 = е –3,016 = 0,049. в) Реакция диссоциации фосгена является реакцией первого порядка. Поэтому количество прореагировавшего фосгена может быть рассчитано по уравнению: С0 – исходная концентрация вещества; C0–x – концентрация к моменту времени t; х – число молей прореагировавшего вещества. Подставляя в это уравнение значение константы скорости реакции, время от начала реакции и исходную концентрацию, решаем уравнение относительно х: 0,5´10 –2 = (1/100) ln [1/(1-х)]; ln [1/(1–x)] = 0,5; ln(1–x) = –0,5; 1–x = е — 0,5 =0,6 и, окончательно, x = 0,4 моля. Таким образом, при температуре 382 о С за 100 минут от начала реакции концентрация фосгена уменьшится от 1 до 0,6 моль/л, так как в каждом литре разложится 0,4 моля фосгена. Задача 23. Во сколько раз возрастет скорость разложения сульфацила натрия в глазных каплях при повышении температуры от 20 до 80 о С? Температурный коэффициент скорости реакции равен 2. то есть скорость разложения возрастет в 64 раза. Задача 24. Рассчитайте время разрушения аэрозольного препарата «Камфомен» на 10%, считая константу скорости разложения основного действующего вещества (фурацилина) равной 1,2´10 –5 час –1 при 20 o С. Решение: Считая исходное количество вещества равным 100%, и используя кинетическое уравнение для реакции 1-го порядка t = ¾ ln ¾¾¾¾ = ¾¾¾¾ = 8775 часов » 1 год. Задача 25. В течение какого времени через раствор сульфата меди необходимо пропускать ток силой 1,5 А, чтобы из него 6,4 г. меди ? Решение: По закону Фарадея масса выделившегося вещества при электролизе (в граммах) m = ЭJt/F, где Э – электрохимический эквивалент вещества J – сила тока (ампер) t – время (Сек) Кулон F – число Фарадея 96494 К/г-экв ( ¾¾¾ ) или 96500 К/г-экв. Электрохимическим эквивалентном называется количества вещества, выраженное в граммах, выделяемое 1к электричества, проходящим через электролит. А – атомная масса; n – валентность t = ¾¾¾ = ¾¾¾¾¾¾ = 12959,8 сек = 216 мин = 3 ч. 36 мин. Примеры решения задач по коллоидной химии Задача 1. Найти поверхностное натяжение анилина s, если сталагмометрическим методом при 20 o С получены следующие данные: число капель анилина n = 42, воды nо=18. Плотность анилина r=1,4´10 3 кг/м 3 ; поверхностное натяжение воды sо=72,75´10 –3 Н/м. Решение: Используем для расчета формулу: s = sо ¾¾¾ = 72,75´10 –3 ¾¾¾¾¾¾ = 43,65´10 –3 Н/м. Задача 2. Найти поверхностное натяжение анилина, если методом наибольшего давления пузырьков получены данные: давление пузырьков при пропускании их через воду равно 11,8 × 10 2 Н/м, а в анилин – 712 Н/м. Температура 20 0 С, поверхностное натяжение воды s0 = 72,75 × 10 -3 Н/м Используем для расчета формулу: s = sН2О ¾¾¾ = 72,75´10 –3 ¾¾¾¾¾¾ = 43,89´10 –3 Н/м. Задача 3. Используя константы уравнения Шишковского (a = 12,6´10 — 3 и b = 21,5), рассчитайте поверхностное натяжение водного раствора масляной кислоты с концентрацией 0,104 моль/л при 273К. Поверхностное натяжение воды при этой температуре s0 = 75,62´10 — 3 Н/м. Решение: С помощью уравнения Шишковского Ds = s0 — s = a ln(1 + bC) рассчитаем поверхностное натяжение раствора s: s = s0 — a ln(1 + bC) = 75,62´10 — 3 -12,6´10 — 3 (1 + 21,5´0,104) = Задача 4. Коллоидный раствор колларгола содержит частицы серебра с диаметром 6´10 –8 см. Определите число частиц, образующихся при диспергировании 0,5 см 3 серебра, удельную поверхность золя и суммарную поверхность частиц, если они имеют: а) сферическую форму с диаметром (d) 6 × 10 -8 см б) кубическую с длиной ребра (ℓ) 10 -6 см. Решение: Зная радиус, можно рассчитать объем одной частицы (сферической) Vч = 4/3pr 3 = 4/3 [3,14 (3´10 –8 ) 3 ] = 113,04´10 –24 см 3 Vкуб. част. = ℓ 3 = (10 -6 ) 3 = 10 -18 см 3 Теперь определим число частиц: n = Vдисп. фазы/Vч = 0,5/113,04´10 –24 = 4,4´10 21 (сферических) n = Vдисп. фазы/Vч = 0,5/10 -18 = 0,5 × 10 18 (кубических) Удельную поверхность системы, содержащей сферические частицы, можно вычислить по формуле Зная Sуд и суммарный объем частиц дисперсной фазы, найдем суммарную поверхность частиц: Sсумм = SудVд.ф. = 10 8 ´0,5 =5´10 7 см 2 (сферич.); Sкуб. = 6´10 6 ´0,5 = 3´10 6 см 2 Sсумм= nSч = n4pr 2 = 4,4´10 21 ·4·3,14·(6´10 — 8 ) 2 = 4,97´10 7 » 5´10 7 см 2 . Задача 5. Определите поверхностный избыток (в кмоль/м 2 ) при 10 о С для водного раствора, содержащего 50 мг/л пеларгоновой кислоты С8Н17СООН. Поверхностные натяжения исследуемого раствора и воды соответственно равны 57´10 –3 Н/м и 74,22´10 –3 Н/м. Решение: Используем уравнение Гиббса: Выразим концентрацию раствора в кмоль/м 3 : С = 0,05/158 = 3,164´10 –4 моль/л = 3,164´10 –4 кмоль/м 3 , (158 – молярная масса пеларгоновой кислоты). Отсюда (57´10 –3 –74,22´10 –3 ) 3,164´10 –4 Г = — ¾¾¾¾¾¾¾¾¾¾ · ¾¾¾¾¾¾ = 7,32´10 –9 кмоль/м 2 . 3,164´10 –4 — 0 8,314´10 3 ´283 Задача 6. Определите длину молекулы масляной кислоты на поверхности раздела «раствор – воздух», если площадь, занимаемая одной молекулой в поверхностном слое, равна 30´10 –20 м 2 , а плотность масляной кислоты r = 978 кг/м 3 . Решение: Длина молекулы l рассчитывается по формуле Учитывая, что S = ¾¾¾ , (где NA-число Авогадро, равное 6,02´10 26 молекул/кмоль), находим предельный поверхностный избыток: S NA 30´10 –20 ´6,02´10 26 Тогда длина молекулы масляной кислоты (М=88): l = ¾¾¾¾¾¾¾ = 4,95´10 –10 » 5´10 –10 м = 5 Å (ангстрем). Задача 7. При изучении адсорбции паров этанола на активированном угле были получены следующие данные:
(р — равновесное давление пара, А — величина адсорбции). Графически определите константы уравнений Фрейндлиха и Ленгмюра. Рассчитайте величину адсорбции при р = 3000 Па. Используя оба уравнения, вычислите, сколько этанола адсорбируется на 5 кг угля. Видео:Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Подготовка к ЕГЭ по ХимииСкачать  Практикум по коллоидной химии (стр. 1 )
ГОУ ВПО «Пятигорская государственная фармацевтическая Кафедра физической и коллоидной химии Видео:СТРОЕНИЕ МИЦЕЛЛЫ - урок 1Скачать  ПРАКТИКУМПО КОЛЛОИДНОЙ ХИМИИ Под общей редакцией заведующей кафедрой физической и коллоидной химии доц. . Рецензенты: сотрудники кафедры неорганической, физической и коллоидной химии Московской медицинской академии им. Сеченова: — , профессор, доктор химических наук, — , доцент, кандидат химических наук. Печатается по решению Проблемной учебно-методической комиссии по химическим дисциплинам Департамента научно-исследовательских и образовательных медицинских учреждений Минздрава России от 01.01.2001 г. Издание 2-ое, исправленное и дополненное. Методическое пособие для студентов к лабораторным занятиям составлено коллективом преподавателей кафедры физической и коллоидной химии Пятигорской государственной фармацевтической академии в соответствии с требованиями Государственного образовательного стандарта на основе «Примерной программы по дисциплине физическая и коллоидная химия для специальности 040500 — Фармация» (Москва, 2002). Материал методического пособия включает описание лабораторных работ по разделам «Поверхностные явления. Адсорбция», «Получение и коагуляция коллоидных систем», «Свойства микрогетерогенных систем» и «Свойства высокомолекулярных веществ и их растворов». Настоящее издание содержит краткий теоретический материал по каждой теме, перечень знаний, умений, навыков, которыми должен овладеть студент при ее изучении, описание приборов и лабораторных установок, а также все необходимые задачи с решениями и вопросы для самоподготовки студентов. (с) ГОУ ВПО Пятигорская государственная фармацевтическая академия ОБЩИЕ УКАЗАНИЯ ПО ТЕХНИКЕ БЕЗОПАСНОСТИ И Требования к оформлению лабораторных работ. 9 ПРАВИЛА ТАБУЛИРОВАНИЯ ВЕЛИЧИН . 10 ПРАВИЛА ПОСТРОЕНИЯ ГРАФИКОВ . 12 ТЕМА 1. ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ. АДСОРБЦИЯ. 14 Работа 1.1. Сталагмометрическое определение поверхностного натяжения водных растворов поверхностно-активных веществ (ПАВ) и расчет размеров их молекул 22 Работа 1.2. Определение концентрации этилового спирта сталагмометрическим методом 27 Работа 1.3. Определение критической концентрации мицеллообразования (ККМ) поверхностно-активных веществ с использованием метода наибольшего давления пузырьков воздуха (по Ребиндеру). 29 Работа 1.4. Изучение адсорбции поверхностно-активных веществ на твёрдых адсорбентах 33 ТЕМА 2. ПОЛУЧЕНИЕ, УСТОЙЧИВОСТЬ И КОАГУЛЯЦИЯ КОЛЛОИД-НЫХ СИСТЕМ. СТРОЕНИЕ МИЦЕЛЛЫ ЛИОФОБНЫХ ЗОЛЕЙ . 37 Работа 2.1. Получение лиофобных коллоидных растворов. 43 Работа 2.2. Определение порогов коагуляции золя гидроксида Работа 2.3. Защитное действие высокомолекулярных веществ. 54 ТЕМА 3. СВОЙСТВА МИКРОГЕТЕРОГЕННЫХ СИСТЕМ . 55 Работа 3.1. Получение и свойства эмульсий. 63 Работа 3.2. Седиментационный анализ суспензий. 69 Работа 3.3. Исследование физических свойств порошков. 75 Работа 3.4. Исследование гидрофильности порошков методом ТЕМА 4. СВОЙСТВА ВЫСОКОМОЛЕКУЛЯРНЫХ ВЕЩЕСТВ И ИХ РАСТВОРОВ 80 Работа 4.1. Изучение кинетики набухания растительного сырья. 86 Работа 4.2. Влияние электролитов и неэлектролитов на набухание белка 90 Работа 4.3. Влияние pH среды на набухание белка. 92 Работа 4.4. Застудневание растворов высокомолекулярных Работа 4.5. Определение средней молярной массы высокомолекулярных веществ вискозиметрическим методом. 96 Работа 4.6. Определение изоэлектрической точки полиэлектролитов (белков) вискозиметрическим методом. А – величина адсорбции a – 1) линейные размеры частиц 2) термодинамическая активность С – молярная концентрация D – 1) степень дисперсности Е – 1) напряжение G – свободная поверхностная энергия g – ускорение силы тяжести Н – 1) напряженность электрического поля I – интенсивность света К – 1) константа адсорбционного равновесия 2) константа скорости коагуляции k – константа Больцмана М – молярная масса NA – число Авогадро n – 1) количество вещества (моль) 2) коэффициент преломления 3) количество частиц Р – коагулирующая способность Q – объемная скорость течения R – универсальная газовая постоянная Sуд – удельная поверхность α – степень набухания Г – поверхностный избыток γ – порог коагуляции Δх – средний сдвиг частиц при броуновском движении δ – толщина двойного электрического слоя ε – диэлектрическая проницаемость ε0 – электрическая постоянная V ζ – электрокинетический потенциал φ – 1) объемная концентрация 2) электротермодинамический потенциал θ – 1) краевой угол смачивания 2) предел текучести ГЛБ – гидрофильно-липофильный баланс ν – частичная концентрация π – 1) геометрическая константа 2) осмотическое давление σ – поверхностное натяжение Методическое пособие «Практикум по коллоидной химии» включает в себя семнадцать лабораторных работ, в том числе методик измерений с использованием торсионных весов, сталагмометра, вискозиметра, прибора Позняка для оценки степени набухания, оптического микроскопа. В описание каждой из них входят цель, устройство и принцип действия используемых приборов, ориентировочная основа действия. Работы сгруппированы в 4 блока в соответствии с тематикой курса коллоидной химии. Во введении к каждой теме приведены: — её значение при изучении смежных дисциплин и для подготовки специалиста-провизора; — перечень знаний, умений и навыков, которыми должен овладеть студент при её изучении; — типовые задачи с решениями. Заключает «Практикум по коллоидной химии» перечень рекомендуемой учебной и справочной литературы. и правила поведения в лаборатории Перед началом работы в новом семестре студенты проходят инструктаж по технике безопасности у ведущего преподавателя и расписываются в специальном журнале. 1. В учебной лаборатории студенту необходимо занять определенное для выполнения текущей работы место и пройти в лаборантскую для получения оборудования и реактивов. 2. Лабораторные работы выполняются студентом в застегнутом (включая рукава) халате и включенной тяге. 3. Запрещается включать аппаратуру и производить химические опыты до получения инструктажа и разрешения преподавателя. 4. Перед началом работы студент обязан внимательно прочитать её описание. Возникшие затруднения необходимо разрешать с преподавателем. 5. Собрав прибор или подготовив аппаратуру для выполнения лабораторной работы, студент должен до начала работы пригласить преподавателя или лаборанта для проверки правильности и безопасности эксплуатации собранной установки. После этого разрешается приступать к работе. 6. Все лабораторные работы должны производиться в последовательности, предусмотренной в разделе «Проведение опыта». Студент обязан четко выполнять распоряжения и указания преподавателя и дежурного лаборанта, касающиеся выполнения работы. 7. При работе в лаборатории необходимо соблюдать тишину и порядок, выключить мобильную связь, поддерживать чистоту на рабочем месте. 8. При использовании реактивов необходимо обращать внимание на надписи на этикетках. Отмерять растворы следует отдельными пипетками. 9. Не допускать попадания кислот, щелочей, фенолов, органических растворителей, растворов солей на кожные покровы. При попадании – смыть под обильной струей воды. При попадании в глаза – промыть водой и обратиться в лечебное учреждение. 10. В лаборатории категорически запрещается использовать открытое пламя, употреблять пищу и напитки, нарушать порядок проведения лабораторной работы. Все манипуляции с летучими, огнеопасными, остро пахнущими веществами (кислоты, органические растворители, фенолы) следует проводить только под тягой. 11. После выполнения лабораторных работ студент обязан показать результаты преподавателю и привести в порядок свое рабочее место, а именно: выключить из сети электрические приборы; вымыть и ополоснуть дистиллированной водой посуду своего комплекта, помыть руки; проверить выключение воды и газа; сдать свое рабочее место дежурному студенту или лаборанту. 12. Перед началом занятий в семестре староста группы назначает дежурных, фамилии которых преподаватель отмечает в кафедральном журнале. Дежурные студенты обычно получают у лаборанта необходимое для всей группы оборудование и литературу, а после окончания занятия – сдают их; принимают рабочие места у студентов после окончания занятия; приводят в порядок лабораторию после занятия и сдают её лаборанту. Требования к оформлению лабораторных работ При оформлении лабораторных работ к ним предъявляются следующие требования. 1. Под датой четко пишется и подчеркивается название работы, цель работы, целевые задачи, методика выполнения эксперимента. 2. Таблицы экспериментальных данных заполняются четко, без помарок и исправлений. 3. Если графики выполнены на отдельном листе они вклеиваются в журнал таким образом, чтобы не закрывать имеющийся на этой странице текст. 4. Все расчеты по уравнениям, включая промежуточные результаты, обязательно должны быть приведены после описания методики эксперимента. 5. Работа должна завершаться формулируемым студентом выводом, кратко и четко отражающим приобретенные знания, умения и навыки, например: 1. Освоена методика сталогмометрического определения поверхностного натяжения водных растворов ПАВ. 2. Графической интерпретацией экспериментальных данных найден предельный поверхностный избыток Г∞. 3. Рассчитаны: площадь (S), толщина, объем занимаемый молекулой ПАВ в адсорбционном слое. Правила табулирования величин, элементарные математические сведения и физико-химические константы Экспериментальные данные для удобства обработки заносятся в таблицы (табулируются). При этом следует руководствоваться следующими правилами: · В заголовки столбцов должны быть четко вписаны названия и размерности приводимых величин. · Данные, относящиеся к растворам одного и того же вещества с различной концентрацией, следует располагать сверху вниз в порядке возрастания концентрации. Название растворителя следует располагать в первой строке столбца. · Если в одной графе приводятся величины с одинаковым десятичным множителем, его удобнее вынести в заголовок столбца. При этом знак степени, в которую возводится число 10, меняется на противоположный (табличное равенство а´102=1,7 подразумевает, что а=1,7´10-2). Пример равнозначной записи данных приведен в таблице. При этом степень точности характеризуется числом значащих цифр (нуль впереди или после других чисел не является значащей цифрой, т. е. в числе 0,00239 только три значащих цифры – 2, 3 и 9, а в числе 23,9800 – четыре). Например, если число 456,395 необходимо представить с точностью до двух значащих чисел, то пишут 4,6×102. До трех – 4,56×102. До четырех – 4,564×102 и т. д. Если в требованиях по представлению чисел содержится фраза «до двух значащих цифр после запятой», то пишут, соответственно, 4,56×102. Т. е. следует различать понятия общего числа значащих цифр и их же числа, но после запятой. · при любых математических операциях с числами следует сохранять число значащих цифр после запятой, как у числа с минимальным их количеством (т. е. при сложении, например, 124,8 + 18,456 + 0,00456, результат следует записывать не так: 143,26056, а так: 143,3). · необходимо соблюдать правила округления – если стоящая за округляемой цифра больше «5», то округляемая цифра увеличивается на единицу (24,77 > 24,8); меньше «5» – не изменяется (24,44 > 24,4); равна «5» – стоящая перед округляемой цифрой нечетная цифра повышается на единицу (24,75 > 24,8), а четная – уменьшается на единицу (2,65 > 2,6). · если действия проводятся с числами в степенной форме, удобнее, если количество значащих цифр до запятой должно будет равно одному (пример неправильной операции – 34,5×10-3×0,234×104, пример правильной операции – 3,45×10-2×2,34×103). Также числа могут преобразовываться так, чтобы показатели степени были одинаковыми (34,5×103 + 0,234×104 = 34,5×103 + 2,34×103 = (34,5 + 2,34)×103 = 3,684×104). · напоминаем, что логарифм – это показатель степени, в которую надо возвести основание логарифма, чтобы получить данное число. Пример: 103=1000 – логарифм тысячи по основанию десять равен трем; ln10=2,303 – логарифм десяти по натуральному основанию равен 2,303. ОСНОВНЫЕ ФИЗИЧЕСКИЕ КОНСТАНТЫ 6,02252 х 1023 моль-1 Универсальная газовая постоянная 0,082057 л·атм/ моль·К Правила построения графиков В большинстве лабораторных работ по физической химии для получения необходимых для расчетов величин используется графический метод. Поскольку точность численных величин, определяемых этим методом, зависит от правильности построения графика, рекомендуется руководствоваться следующими правилами: · график строится, как правило, на миллиметровой (координатной) бумаге. · для обозначения осей координат должны использоваться общепринятые обозначения величин с обязательным указанием их размерности (если она имеется). Значение независимой переменной откладывается по оси абсцисс, зависимой — по оси ординат. · масштаб выбирается так, чтобы изображение (собственно график) по возможности занимало все координатное поле. · на осях координат ставятся через равные промежутки отметки, соответствующие кратным масштабным числам. Во избежание неточностей при отсчете и загромождения графика на осях координат не отмечаются точки, соответствующие экспериментальным данным. · экспериментальные точки наносятся на координатное поле остро заточенным карандашом. Они должны быть ясно видны, даже если на них накладывается линия. При необходимости точки, принадлежащие разным функциям, могут быть выделены цветом, конфигурацией (например, Если это специально не оговорено или не диктуется характером исследуемой зависимости, экспериментальные точки соединяются плавными усредняющими кривыми, проводимыми с помощью лекал, или усредняющими прямыми, проводимыми по линейке. Если есть возможность, то при достаточном числе точек линия может быть проведена с помощью обработки данных на ЭВМ. Пример построения графика зависимости поверхностного натяжения раствора от концентрации поверхностно-активного вещества (изотерма поверхностного натяжения): Если искомая величина находится экстраполяцией прямолинейного графика, то линия продолжается до пересечения с осью координат по линейке пунктиром. Если она определяется интерполяцией, то исходная и искомая точки соединяются с графиком также пунктиром. ТЕМА 1. ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ. АДСОРБЦИЯ Значение темы для фармации определяется тем, что многие лекарственные формы (порошки, таблетки, суспензии, эмульсии и др.) являются дисперсными системами с развитой поверхностью. Их удельная поверхность может достигать многих десятков и даже сотен квадратных метров на грамм дисперсной фазы. Поверхностные явления в таких системах в значительной степени определяют их свойства и поведение при изготовлении и хранении. Они играют существенную роль и при высвобождении фармакологически активных веществ из лекарственных форм, их всасывании и транспорте через биологические мембраны внутри организма. Кроме того, методы, связанные с измерением поверхностного натяжения, используются для изучения ряда физико-химических свойств различных веществ, в том числе площади, занимаемой молекулой при адсорбции на поверхности, длины молекулы, поверхностной активности и адсорбируемости веществ и др. Сталагмометрический метод может быть использован для определения концентрации поверхностно-активных веществ в растворе. Изучение основ учения об адсорбции необходимо будущему провизору, так как различные процессы фармакокинетики и фармакодинамики лекарственных веществ обязательно включают в себя стадию адсорбции. Адсорбция используется и в терапевтических целях, например, для извлечения из желудочно-кишечного тракта ядовитых веществ, попавших в организм, а также для очистки лекарственных веществ на различных стадиях их получения. Такой универсальный метод исследования и анализа, как хроматография, имеет в своей основе адсорбцию веществ на различных поверхностях раздела. Ионообменная адсорбция служит для избирательного выделения ионов из сложных смесей, для умягчения и обессоливания воды. На ней также основан принцип действия ионоселективных электродов, в том числе стеклянных электродов, применяемых для потенциометрического определения рН. Изучив данную тему и выполнив лабораторные работы, относящиеся к ней, студент должен знать: — строение поверхностного слоя и его отличительные особенности; — строение молекул поверхностно-активных веществ (ПАВ), влияние ПАВ на поверхностное натяжение растворов; — основы теории адсорбции на поверхностях раздела «жидкость – газ», «жидкость – жидкость», «твердое тело – газ», «твердое тело — жидкость»; — уравнения Шишковского, Гиббса, Ленгмюра, Фрейндлиха и их применение; — расчетные формулы используемых экспериментальных методов; — значение адсорбции для хроматографии; — устройство и принцип действия приборов для измерения поверхностного натяжения. Студент должен уметь: — проводить измерения с помощью сталагмометра Траубе и прибора Ребиндера; — рассчитывать поверхностное натяжение, поверхностную активность, величину адсорбции и поверхностного избытка ПАВ, размеры их молекул; — определять концентрацию растворов ПАВ. Студент должен приобрести или закрепить навыки: — приготовления, разбавления и отмеривания растворов; — расчета концентрации веществ в растворах; — табулирования величин, построения и анализа графиков; — пользования справочной литературой. Молекулы поверхностного слоя жидкостей имеют часть неиспользованных сил сцепления, которые представляют собой избыточную энергию. Эта избыточная энергия молекул поверхностного слоя называется свободной поверхностной энергией (G). Она определяется величиной поверхностного натяжения (σ) и суммарной поверхностью раздела фаз (S) и рассчитывается по уравнению: — Поверхностное натяжение определяется как энергия переноса молекул из объема фаз на поверхность или как работа образования единицы поверхности раздела: — Поверхностное натяжение воды на границе с воздухом равно σ20ºС = 72,75×10-3 Н/м — Если в такую двухфазную систему (вода-воздух или вода-жидкость) ввести третье вещество с другим значением поверхностного натяжения, то оно после растворения изменит поверхностное натяжение на границе раздела. — Вещества, понижающие поверхностное натяжение называются поверхностно-активными (ПАВ). К ним относится большинство органических веществ с меньшим поверхностным натяжением, чем у воды: кислоты, мыла, спирты, фенолы, амины, пектины, полисахариды/ смачиватели и др. — Вещества повышающие поверхностное натяжение (неорганические электролиты – соли, щелочи) называются поверхностно-инактивными (ПИАВ). Некоторые ПАВ способны к мицеллообразованию – образованию агрегатов дифильных молекул разной формы в зависимости от концентрации. Концентрация, при которой происходит мицеллообразование, называется критической концентрацией мицеллообразования (ККМ). — Зависимость поверхностного натяжения растворов ПАВ от концентрации выражается изотермой поверхностного натяжения, которая может быть описана с помощью уравнения Шишковского: где a, b константы. понижение поверхностного натяжения раствора ПАВ с концентрацией С по сравнению с поверхностным натяжением растворителя (σ0). — Уменьшение поверхностного натяжения может происходить в результате самопроизвольного концентрирования в поверхностном слое веществ – процесса адсорбции (Г, моль/см2, Кмоль/м2). — Адсорбция на поверхности раздела фаз жидкость-газ или жидкость-жидкость определяется по формуле Гиббса: где ( — Адсорбция на поверхности раздела «твердое тело – газ» (А) возможная как физическая так и хемосорбция. Величину А рассчитывают по разнице концентраций адсорбированного вещества в растворе до и после адсорбции (∆С = С0 — С). Адсорбцию выражают числом молей адсорбированного вещества на единицу массы адсорбента (моль/г, кмоль/кг). Тогда величина экспериментальной адсорбции: — Величина адсорбции зависит от природы адсорбента, концентрации адсорбента, температуры и др. Поэтому, в расчетах ее величины используют уравнение Ленгмюра: где А∞ – предельная мономолекулярная адсорбция; c, p – равновесные концентрация и давление; b – константа адсорбционного равновесия. и уравнение Фрейндлиха: где К и 1/n – константы; С, p – равновесные концентрация или давление. ВОПРОСЫ ТЕОРЕТИЧЕСКОГО МИНИМУМА ДЛЯ САМОПОДГОТОВКИ: 1. Гетерогенность и дисперсность как основные признаки объектов коллоидной химии. Размеры частиц, степень дисперсности, удельная поверхность системы и их взаимосвязь. 2. Поверхностные явления и их значение в фармации. Свободная поверхностная энергия и поверхностное натяжение. 3. Пути уменьшения свободной поверхностной энергии дисперсных систем. 4. Поверхностно-активные вещества (ПАВ) и их классификация. 5. Характеристики ПАВ — гидрофильно-липофильный баланс (ГЛБ) и поверхностная активность. Правило Дюкло — Траубе. 6. Изотерма поверхностного натяжения. Уравнение Шишковского. 7. Мицеллообразование в растворах ПАВ. Критическая концентрация мицеллообразования (ККМ и ККМ). Солюбилизация, её применение в фармации. Липосомы. 8. Адсорбция (общие понятия). Адсорбция ПАВ на поверхностях раздела «жидкость – газ» и «жидкость – жидкость». Уравнение Гиббса. 9. Адсорбция на поверхности раздела «твёрдое тело – газ». Изотерма адсорбции. Экспериментальное определение величины адсорбции. 10. Теория мономолекулярной адсорбции Ленгмюра. Вывод уравнения Ленгмюра. Физический смысл коэффициентов этого уравнения. 11. Расчет коэффициентов уравнения Ленгмюра. Применимость уравнения. 12. Уравнение Фрейндлиха. Расчет его коэффициентов. Применимость уравнения. 13. Адсорбция на поверхности раздела «твёрдое тело – жидкость». Правило уравнивания полярностей Ребиндера. РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ Задача 1. Найти поверхностное натяжение анилина, если сталагмометрическим методом при 20ºС получены следующие данные: число капель анилина – 42, число капель воды – 18. Плотность анилина 1400 кг / м3. РЕШЕНИЕ. Используем для расчета формулу (Поверхностное натяжение воды и её плотность, соответственно равные 72,75 × 10-3 Н/м и 1000 кг/м, берутся из справочника). Задача 2. Определить поверхностный избыток Г¥ (кмоль/м2 ) при 10ºС для водного раствора, содержащего в 1 литре 50 мг пеларгоновой кислоты С8Н17СООН. Поверхностные натяжения исследуемого раствора и воды соответственно равны 57,00×10-3 и 74,22×10-3 Н/м. РЕШЕНИЕ. Используем уравнение Гиббса: где С – молярная концентрация пеларгоновой кислоты (С = g / М = 0,05 / 158 = 0,000316 моль/л; 158 – молярная масса), Ds – изменение поверхностного натяжения раствора по сравнению с водой [Ds = (57,00 — 74,22) × 10-3 = -17,22 × 10-3 Н/м], DС – разность концентраций (в данном случае С = 0,000, R – универсальная газовая постоянная, Т – температура в К. Задача 3. Рассчитать длину l молекулы масляной кислоты на поверхности раздела «водный раствор – воздух», если площадь S, занимаемая одной её молекулой в поверхностном слое, равна 30 × 10-20 м2. Плотность масляной кислоты – 978 кг/м3. РЕШЕНИЕ. Длину молекулы можно рассчитать по формуле где М — молярная масса кислоты, Г – предельный поверхностный избыток её в адсорбционном слое, r – плотность. Задача 4. При изучении адсорбции этанола на активированном угле при 18оС были получены данные: р × 10-2, Па 5,33 9,87 17,33 23,06 45,53 x/m 103, м3 / кг 14,9 19,1 24,2 27,3 36,8 Определить графическим способом константы уравнений Фрейндлиха и Ленгмюра и рассчитать с их помощью величину адсорбции при р = 3000 Па, а также количество этанола, адсорбирующегося на 5 кг угля. РЕШЕНИЕ. Для нахождения констант уравнения Фрейндлиха x/m = kр1/n строится график зависимости lg x/m = f(lg р). Находим необходимые величины: lg x/m -1,183 -1,720 -1,62 -1,51 -1,43 lg р 2,60 2,87 3,114 3,24 3,53
и строим по ним график. Он отсекает от оси ординат отрезок 0К, равный lg k = = -3,65. Отсюда k = 10-3,65 = 2,34×10-4. По тангенсу угла наклона находим второй коэффициент: 1/n = tg a МL / KL = 0,67м3. А = x/m = kр1/n = 2,34×10-4×30000,67 = 33,49×10-3 м3/кг, и значит, на 5 кг угля адсорбируется 5×33,49×10-3 = 0,167 м3 этанола. 📹 ВидеоХимические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать  Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать  Решение биквадратных уравнений. 8 класс.Скачать  Расчеты по уравнениям химических реакций. 1 часть. 8 класс.Скачать  Составление уравнений химических реакций. 1 часть. 8 класс.Скачать  ОВР и Метод Электронного Баланса — Быстрая Подготовка к ЕГЭ по ХимииСкачать  Как за 4 МИНУТЫ выучить Химию? Химическое Количество, Моль и Закон АвогадроСкачать  Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать  РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать  8 класс. ОВР. Окислительно-восстановительные реакции.Скачать  10 класс § 10 "Коллоидные растворы"Скачать  Как решают уравнения в России и США!?Скачать  Химические уравнения. СЕКРЕТНЫЙ СПОСОБ: Как составлять химические уравнения? Химия 8 классСкачать  Гальванические элементы. 1 часть. 10 класс.Скачать  Расстановка Коэффициентов в Химических Реакциях // Подготовка к ЕГЭ по ХимииСкачать  |

 KV1 4 0,0017·1000 4
KV1 4 0,0017·1000 4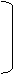
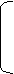 Массу экстрагированного вещества можно рассчитать и с помощью другого уравнения:
Массу экстрагированного вещества можно рассчитать и с помощью другого уравнения:

 – длина
– длина – скорость
– скорость , о) и т. п. Как правило, точки не соединяются посторонними линиями с осями координат.
, о) и т. п. Как правило, точки не соединяются посторонними линиями с осями координат.

 ,
,
 ,
, – поверхностная активность, характеризующая способность вещества понижать σ и переходить из объема на поверхность.
– поверхностная активность, характеризующая способность вещества понижать σ и переходить из объема на поверхность. , где V – объем раствора, m – масса адсорбента.
, где V – объем раствора, m – масса адсорбента. или
или  ,
, или
или  ,
,





