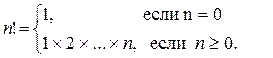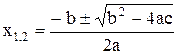 |
Задача хорошо знакома из математики. Исходными данными здесь являются коэффициенты a, b, c. Решением в общем случае являются два корня x1 и x2, которые вычисляются по формулам:
Все величины, используемые в этой программе, имеют вещественный тип.
алг корни квадратного уравнения
вещ a, b, c, x1, x2, d
начввод a, b, c
Кон
Слабость такого алгоритма видна «невооруженным глазом». Он не обладает важнейшим свойством, предъявляемым к качественным алгоритмам: универсальностью по отношению к исходным данным. Какими бы ни были значения исходных данных, алгоритм должен приводить к определенному результату и выходить на конец. Результатом может быть числовой ответ, но может быть и сообщение о том, что при таких данных задача решения не имеет. Недопустимы остановки в середине алгоритма из-за невозможности выполнить какую-то операцию. Это же свойство в литературе по программированию называют результативностью алгоритма (в любом случае должен быть получен какой-то результат).
Чтобы построить универсальный алгоритм, сначала требуется тщательно проанализировать математическое содержание задачи.
Решение уравнения зависит от значений коэффициентов a, b, c. Вот анализ этой задачи (ограничиваемся только поиском вещественных корней):
если a=0, b=0, c=0, то любое х – решение уравнения;
если a=0, b=0, c¹0, то уравнение решений не имеет;
если a=0, b¹0, то это линейное уравнение, которое имеет одно решение: x=–c/b;
если a¹0 и d=b 2 -4ac³0, то уравнение имеет два вещественных корня (формулы приведены выше);
кв
кв
Кон
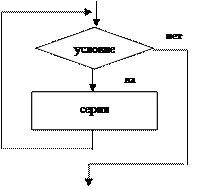
В этом алгоритме многократно использована структурная команда ветвления. Общий вид команды ветвления в блок-схемах и на алгоритмическом языке следующий:
| еслиусловие то серия 1 иначе серия 2 кв |
Вначале проверяется «условие» (вычисляется отношение, логическое выражение). Если условие истинно, то выполняется «серия 1» – последовательность команд, на которую указывает стрелка с надписью «да» (положительная ветвь). В противном случае выполняется «серия 2» (отрицательная ветвь). В АЯ условие записывается после служебного слова «если», положительная ветвь – после слова «то», отрицательная – после слова «иначе». Буквы «кв» обозначают конец ветвления.
Если на ветвях одного ветвления содержатся другие ветвления, то такой алгоритм имеет структуру вложенных ветвлений. Именно такую структуру имеет алгоритм «корни квадратного уравнения». В нем для краткости вместо слов «да» и «нет» использованы соответственно «+» и «–».
Рассмотрим следующую задачу: дано целое положительное число n. Требуется вычислить n! (n-факториал). Вспомним определение факториала.
Ниже приведена блок-схема алгоритма. В нем используются три переменные целого типа: n – аргумент; i – промежуточная переменная; F – результат. Для проверки правильности алгоритма построена трассировочная таблица. В такой таблице для конкретных значений исходных данных по шагам прослеживается изменение переменных, входящих в алгоритм. Данная таблица составлена для случая n=3.
| Шаг | n | F | i | Условие | |
| вывод | 1£3, да 2£3, да 3£3, да 4£3, нет |
Трассировка доказывает правильность алгоритма. Теперь запишем этот алгоритм на алгоритмическом языке.
алгФакториал
целn, i, F
нач ввод n
F:=1; i:=1
пока i£n, повторять
нц F:=F´i
кц
Кон
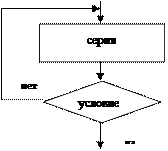
Этот алгоритм имеет циклическую структуру. В алгоритме использована структурная команда «цикл-пока», или «цикл с предусловием». Общий вид команды «цикл-пока» в блок-схемах и в АЯ следующий:
| пока условие, повторять нц серия кц |
Повторяется выполнение серии команд (тела цикла), пока условие цикла истинно. Когда условие становится ложным, цикл заканчивает выполнение. Служебные слова «нц» и «кц» обозначают соответственно начало цикла и конец цикла.
Цикл с предусловием – это основная, но не единственная форма организации циклических алгоритмов. Другим вариантом является цикл с постусловием. Вернемся к алгоритму решения квадратного уравнения. К нему можно подойти с такой позиции: если a=0, то это уже не квадратное уравнение и его можно не рассматривать. В таком случае будем считать, что пользователь ошибся при вводе данных и следует предложить ему повторить ввод. Иначе говоря, в алгоритме будет предусмотрен контроль достоверности исходных данных с предоставлением пользователю возможности исправить ошибку. Наличие такого контроля – еще один признак хорошего качества программы.
 | алгквадратное уравнение вещa, b, c, d, x1, x2 нач повторять ввод a, b, c до a¹0 d:=b 2 –4ac если d³0 тоx1:=(–b+Öd)/(2a) x2:=(–b–Öd)/(2a) вывод x1, x2 иначе вывод “нет вещественных корней” кв кон |
В общем виде структурная команда «цикл с постусловием» или «цикл-до» представляется так:
| повторять серия доусловие |
Здесь используется условие окончания цикла. Когда оно становится истинным, цикл заканчивает работу.
Составим алгоритм решения следующей задачи: даны два натуральных числа M и N. Требуется вычислить их наибольший общий делитель – НОД(M,N).
Эта задача решается с помощью метода, известного под названием алгоритма Евклида. Его идея основана на том свойстве, что если M>N, то НОД(M N то M:=M–N иначе N:=N–M кв кц кон
Алгоритм имеет структуру цикла с вложенным ветвлением. Проделайте самостоятельно трассировку этого алгоритма для случая M=18, N=12. В результате получится НОД=6, что, очевидно, верно.
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Решить квадратное уравнение
Найти корни квадратного уравнения и вывести их на экран, если они есть. Если корней нет, то вывести сообщение об этом. Конкретное квадратное уравнение определяется коэффициентами a , b , c , которые вводит пользователь.
Квадратное уравнение имеет вид ax 2 + bx + c = 0 . Коэффициенты a , b и c — это конкретные числа, а x надо найти, решив уравнение.
- Вычислить дискриминант по формуле d = b 2 — 4ac .
- Если дискриминант больше нуля, то вычислить два корня уравнения:
x1 = (-b+√d) / 2a
x2 = (-b-√d) / 2a - Если дискриминант равен нулю, то вычислить только один корень (второй будет равен ему).
- Если дискриминант отрицателен, то вывести сообщение, что корней нет.
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Pascal
квадратное уравнение паскаль
Видео:ПРОСТЕЙШИЙ способ решения Квадратного Уравнения #shorts #youtubeshortsСкачать
Язык Си
Ключ -lm при компиляции gcc.
Видео:САМЫЙ ЛЕГКИЙ способ решения Квадратного Уравнения #shorts #youtubeshortsСкачать

Python
Видео:Как решать квадратные уравнения без дискриминантаСкачать

КуМир
Видео:34 Задача: Найти корни квадратного уравнения при помощи PythonСкачать

Basic-256
- Total 0
- 0
- 0
- 0
- 0
квадратное уравнение паскаль
var
a,b,c,d,x1,x2: real;
begin
write(‘a=’); readln(a);
write(‘b=’); readln(b);
write(‘c=’); readln(c);
d := b*b — 4*a*c;
if d > 0 then begin
x1 := (-b + sqrt(d)) / (2*a);
x2 := (-b — sqrt(d)) / (2*a);
writeln(‘x1=’,x1:3:2,’; x2=’,x2:3:2);
end
else
if d = 0 then begin
x1 := (-b) / (2*a);
writeln(‘x=’,x1:5:2);
end
else
writeln(‘Корней нет’);
end.
main() <
float a,b,c,d,x1,x2;
printf(«a=»); scanf(«%f»,&a);
printf(«b=»); scanf(«%f»,&b);
printf(«c=»); scanf(«%f»,&c);
d = b*b — 4*a*c;
if (d>0) <
x1 = (-b + sqrt(d)) / (2*a);
x2 = (-b — sqrt(d)) / (2*a);
printf(«x1=%.2f; x2=%.2f», x1, x2);
>
else
if (d = 0) <
x1 = -b / (2*a);
printf(«x1=%.2f; x2=%.2f», x1, x2);
>
else printf(«Корней нет.»);
printf(«n»);
>
Ключ -lm при компиляции gcc.
python квадратное уравнение
print(«Введите коэффициенты для квадратного уравнения (ax^2 + bx + c = 0):»)
a = float(input(«a = «))
b = float(input(«b = «))
c = float(input(«c = «))
discr = b**2 — 4 * a * c;
print(«Дискриминант D = %.2f» % discr)
if discr > 0:
import math
x1 = (-b + math.sqrt(discr)) / (2 * a)
x2 = (-b — math.sqrt(discr)) / (2 * a)
print(«x1 = %.2f nx2 = %.2f» % (x1, x2))
elif discr == 0:
x = -b / (2 * a)
print(«x = %.2f» % x)
else:
print(«Корней нет»)
input «a = «, a
input «b = «, b
input «c = «, c
d = b^2 — 4*a*c
if d > 0 then
x1 = (-b + sqrt(d)) / (2*a)
x2 = (-b — sqrt(d)) / (2*a)
print «x1 = » + x1 + «, x2 = » + x2
else
if d = 0 then
x = -b / (2*a)
print «x = » + x
else
print «Корней нет»
endif
endif
Команда decimal указывает сколько знаков после запятой следует выводить.
Видео:Как решить квадратное уравнение (Положительный дискриминант)Скачать
Программирование на Паскале. Тема: «Решение квадратного уравнения с использованием конструкции IF–THEN–ELSE»
Цели урока:
Оборудование:
До сих пор мы с вами говорили о каких-то отвлечённых задачах из области математики. Сегодня мы поговорим о конкретной задаче, которая встречается у вас почти на каждом уроке. Это решение квадратного уравнения. Я хочу, чтобы вы на примере этой задачи поняли, что программирование — это не просто прихоть учителя, это действительно раздел информатики, который может нам помочь, например, в решении конкретных математических задач. Нужно только уметь разбираться в этом.
2. Математическое решение
Давайте вспомним, что понимают под квадратным уравнением?
Что из себя представляют числа a,b,c и как их называют?
С чего начинают решение квадратного уравнения?
Найдите вокруг себя формулу дискриминанта. (D=b 2 -4ac) (Приложение 3)
Как мы решаем далее квадратное уравнение? (сравнение D с нулём)
Какие выводы мы из этого делаем?
(если D 0, то два корня)
Как найти корни квадратного уравнения? Найдите формулы корней среди тех, что развешены повсюду.
Если я случай наличия корней квадратного уравнения сведу к условию D
(Два одинаковых корня)
Давайте ещё раз подробно разберём нашу задачу:
Итак, у нас есть квадратное уравнение ax 2 +bx+c=0.
Мы должны решить его, т.е. найти такие значения х, при которых правая часть уравнения =0. Мы знаем, что для этого нам надо:
Найти дискриминант D=b 2 — 4ac.
Сравнить его с нулём
D=b 2 -4ac=10 2 -4*3*3=100 — 36 =64
Х1=
X2 =
3. Составление блок-схемы алгоритма.
По заданному решению попробуем составить блок-схему алгоритма в тетради. Кто справится первым, прошу к доске.
Подпишем основные элементы блок — схемы применительно к языку программирования.
4. Составление программы по блок — схеме.
Теперь, пользуясь нашими записями, составим программу и покажем её учителю. Тот, кто до конца урока составит только программу, не проверив её на компьютере, получит три, тот, кто наберёт программу на компьютере, но не проверит её на примерах, получит три. Тот, кто выполнит всё задание, получит пять.
А я раздам вам домашнее задание.
Var a,b,c,d,x1,x1: real;
Write(‘введите коэффициенты уравнения a,b,c’); readln(a,b,c);
Else writeln(‘действительных корней нет’)
1. Составить и набрать программу КВУР на компьютере.
Загрузка среды Pascal- 2ЩЛКМ по значку Pascal, нажать ALT+ENTER.
Запуск программы — ЩЛКМ по кнопке RUN выбрать RUN.
2. Решить следующие квадратные уравнения и показать учителю их решения (если нет такой возможности, то занести их в маршрутный лист (Приложение 4)
1,5х 2 -0,6х — 4,8 = 0
3. Переделайте программу КВУР таким образом, чтобы в ней учитывался случай, когда D=0 и уравнение имеет один корень.
4. Закрыть программу.
Подсказка: Меню File — Exit или ALT+X.
1. За простое воспроизведение (набор программы) без проверки оценка «3»
2. За проверку работы программы на примерах, представленных учителем оценка «4»
3. За решение всех заданий и дополнительное изменение программы для случая D=0, оценка «5»
4. Закрыть программу.
Подсказка: Меню File — Exit или ALT+X.
| № | Х1 | Х2 |
| 1 | 3,230139 | 0,1031947 |
| 2 | 1,464102 | -5,464102 |
| 3 | 1,106107 | -1,356107 |
| 4 | Корней нет | |
| 5 | Корней нет | |
| 6 | 1,6 | 0 |
| 7 | 2 | -1,6 |
| 8 | Корней нет | |
| 9 | 0,6872614 | -1,131706 |
| 10 | 9,486833 | -9,486833 |
Можно дать дополнительное задание:
Изменить программу так, чтобы ответ был с точностью до 2-х знаков после запятой.
1) Напишите программу проверки пароля. Пусть пароль — некоторое число, зафиксированное в программе. Программа печатает приглашение «введите пароль» и вводит число. Если введённое число совпадает с фиксированным паролем, то программа выводит приветствие, если нет — сообщает о том, что пароль не угадан.
7. Подведение итогов урока.
Итак, ребята, сегодня мы с вами решали конкретные задачи из математики, применяя свои умения по программированию. Вы получили следующие оценки за свои знания. (Перечисление оценок) На следующем уроке нам предстоит познакомиться с новыми алгоритмами — Циклическими.
На сегодня наш урок закончен. До свидания.
Литература:
💡 Видео
Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Программа для решения корней квадратного уравнения с использованием дискриминанта на языке ПаскальСкачать
Решение биквадратных уравнений. 8 класс.Скачать

РЕШЕНИЕ НЕПОЛНОГО КВАДРАТНОГО УРАВНЕНИЯ ЗА 5 СЕКУНДСкачать

Алгоритм решения квадратного уравнения | Алгебра 8 класс #35 | ИнфоурокСкачать

Квадратные уравнения #shorts Как решать квадратные уравненияСкачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать

Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Квадратное уравнение. 1 урок.Скачать

Программа, определяющая корни квадратного уравнения. Язык программирования Python.Скачать

Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать