Решение задачи на общее уравнение динамики (5 видео)

Общее уравнение динамики. Пример решения задачи

Содержание

Условие задачи
Решение задачи
Установление кинематических соотношений
Активные внешние силы
Силы инерции
Применение общего уравнения динамики
Определение суммы работ внешних активных сил и сил инерции
Общее уравнение динамики – теорема Даламбера-Лагранжа — решение задач по теоретической механике
Задачи на тему Общее уравнение динамики
🎬 Видео

Видео:Общее уравнение динамики. Задача 1Скачать

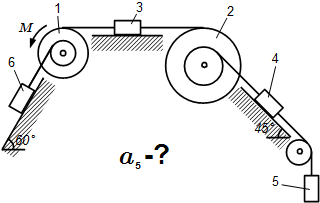
Условие задачи

Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3-6, прикрепленных к этим нитям, и невесомого блока. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом M = 10 Н·м , приложенной к шкиву 1. Радиусы ступеней шкива 1 равны: R ₁ = 0,2 м , r ₁ = 0,1 м , а шкива 2 – R ₂ = 0,3 м , r ₂ = 0,15 м ; их радиусы инерции относительно осей вращения равны соответственно ρ ₁ = 0,1 м и ρ ₂ = 0,2 м .

Пренебрегая трением, определить ускорение груза 5. Веса шкивов и грузов заданы: P ₁ = 40 Н , P ₂ = 0 , P ₃ = 0 , P ₄ = 20 Н , P ₅ = 30 Н , P ₆ = 10 Н . Грузы, веса которых равны нулю, на чертеже не изображать.

Указание. При решении задачи использовать общее уравнение динамики (принцип Даламбера – Лагранжа).

Видео:§5.4.1. Общее уравнение динамикиСкачать

Решение задачи

Дано: R ₁ = 0,2 м , r ₁ = 0,1 м , R ₂ = 0,3 м , r ₂ = 0,15 м , ρ ₁ = 0,1 м , ρ ₂ = 0,2 м . P ₁ = 40 Н , P ₂ = 0 , P ₃ = 0 , P ₄ = 20 Н , P ₅ = 30 Н , P ₆ = 10 Н , M = 10 Н·м .

Установление кинематических соотношений

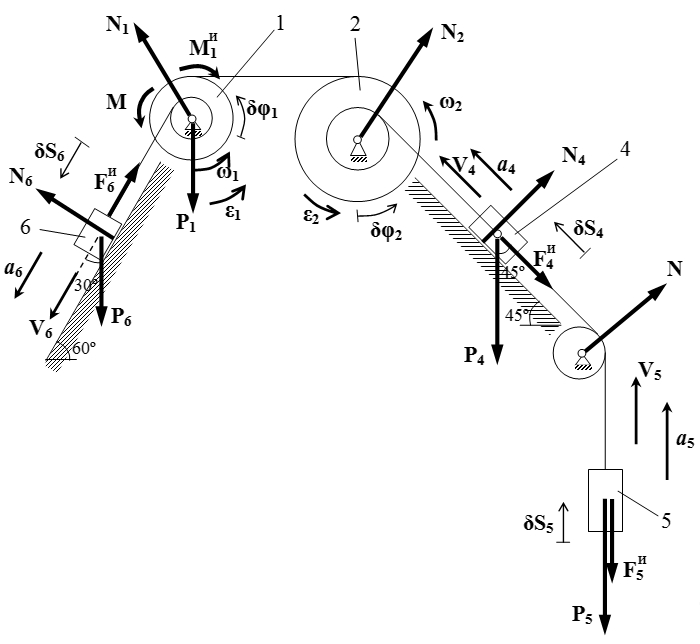
Установим кинематические соотношения. Пусть V ₄ , V ₅ , V ₆ , a ₄ , a ₅ , a ₆ , δS ₄ , δS ₅ , δS ₆ – скорости, ускорения и малые перемещения грузов 4,5 и 6. Пусть ω ₁ , ω ₂ , ε ₁ , ε ₂ , δφ ₁ , δφ ₂ – угловые скорости, угловые ускорения и малые углы поворота шкивов 1 и 2.

Скорость движения нити между телами 2, 4 и 5:
. Отсюда .
Скорость движения нити между шкивами 1 и 2:
. Отсюда
.
Скорость движения нити между телами 1 и 6:
.

Итак, мы нашли связь между скоростями тел.
;
;
.

Поскольку ускорения – это производные скоростей по времени, ,
то дифференцируя по времени предыдущие формулы, находим связь между ускорениями:
;
;
.

Поскольку скорости – это производные от перемещений по времени, то такая же связь есть между бесконечно малыми перемещениями.
;
;
.

Активные внешние силы

Рассмотрим внешние силы, действующие на систему.
Это силы тяжести тел P ₁ = 40 Н , P ₄ = 20 Н , P ₅ = 30 Н и P ₆ = 10 Н , направленные вниз;
заданная пара сил с моментом M = 10 Н·м ;
силы давления осей N ₁ , N ₂ и N шкивов 1, 2 и невесомого блока;
силы реакции N ₄ и N ₆ , действующие на грузы со стороны поверхностей, перпендикулярные этим поверхностям.

Силы инерции

Мы будем решать эту задачу с помощью общего уравнения динамики, применяя принцип Даламбера — Лагранжа. Он заключается в том, что сначала мы вводим силы инерции. После введения сил инерции, задача динамики превращается в задачу статики. То есть нам нужно найти неизвестные силы инерции, чтобы система находилась в равновесии. Данную задачу статики мы решаем, применяя принцип Даламбера. То есть считаем, что система совершила малое перемещение. Тогда в равновесии, сумма работ всех сил, при таком перемещении, равна нулю.

Итак, на первом этапе мы вводим силы инерции. Для этого предполагаем, что система движется с некоторым, пока не определенным, ускорением. То есть шкивы 1 и 2 вращаются с угловыми ускорениями ε ₁ и ε ₂ , соответственно; грузы 4,5 и 6 совершают поступательное движение с ускорениями a ₄ , a ₅ и a ₆ , соответственно. Между этими ускорениями имеются связи, которые мы нашли ранее. То есть все эти ускорения можно выразить через одно ускорение a ₅ . Силы инерции определяются так, что они равны по модулю и противоположны по направлению тем силам (и моментам сил), которые, по законам динамики, создавали бы предполагаемые ускорения (при отсутствии других сил).

Определяем модули (абсолютные значения) сил и моментов инерции и выражаем их через a ₅ .
Пусть – массы тел;
– момент инерции шкива 1.
Момент сил инерции, действующий на шкив 1:
.
Силы инерции, действующие на грузы 4, 5 и 6:
;
;
.

Изображаем силы инерции на чертеже учитывая, что их направления противоположны ускорениям.

Применение общего уравнения динамики

Даем системе бесконечно малое перемещение. Пусть груз 5 переместился на малое расстояние δS ₅ . Тогда угол поворота δφ ₁ шкива 1 и перемещения δS ₄ и δS ₆ грузов 4 и 6 определяются с помощью установленных ранее кинематических соотношений. Поскольку нити нерастяжимые, то они не совершают работу при таком перемещении. Это означает, что система имеет идеальные связи. Поэтому мы можем применить общее уравнение динамики:
,
согласно которому сумма работ всех активных сил и сил инерции, при таком перемещении, равна нулю.

Определение суммы работ внешних активных сил и сил инерции

Работа, которую совершает сила при перемещении точки ее приложения на малое смещение равна скалярному произведению векторов , то есть произведению модулей векторов F и ds на косинус угла между ними.

Работа, произведенная моментом сил , вычисляется аналогично:
.

Определяем работы всех активных сил и сил инерции. Поскольку центры осей шкивов 1, 2 и невесомого блока не совершают перемещений, то силы P ₁ , N ₁ , N ₂ и N не совершают работу. Поскольку силы N ₄ и N ₆ перпендикулярны перемещениям грузов 4 и 6, то эти силы также не совершают работу.

Находим сумму работ остальных активных сил и сил инерции.

.
Подставляем выражения для сил инерции и применяем кинематические соотношения.

.
Сокращаем на δS ₅ и преобразовываем.

.
Подставляем численные значения.

;
;
м/с 2 .

Автор: Олег Одинцов . Опубликовано: 02-08-2015

Видео:Общее уравнение динамики. Расчет механической системы.Скачать

Общее уравнение динамики – теорема Даламбера-Лагранжа — решение задач по теоретической механике

Ищите кому заказать термех — пишите мне вк

Примеры моих работ: Пример2 Пример2 Пример3

Общее уравнение динамики применяется для решения задач по термеху в случаях если необходимо определит ускорение какого либо тела, или всех тел. Иногда задачи на общее уравнение динамики просят решить используя теорему Даламбера – Лагранжа, или типа того. Это одно и тоже: общее уравнение динамики и теорема Даламбера – Лагранжа. Лично я больше предпочитаю первое название. Суть общего уравнения динамики очень проста: сумма бесконечно малых работ внешних сил и сил инерции, на бесконечно малом возможном (БМВ) перемещении системы, равна нулю.

Вход на сайт

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Задачи на тему Общее уравнение динамики

Динамика:
Аналитическая механика
§ 47. Общее уравнение динамики

Задачи с решениями

47.1 Три груза массы M каждый соединены нерастяжимой нитью, переброшенной через неподвижный блок A. Два груза лежат на гладкой горизонтальной плоскости, а третий груз подвешен вертикально. Определить ускорение системы и натяжение нити в сечении ab. Массой нити и блока пренебречь.
РЕШЕНИЕ

47.2 Решить предыдущую задачу с учетом массы блока, считая, что при движении грузов блок A вращается вокруг неподвижной оси. Масса блока сплошного однородного диска равна 2M.
РЕШЕНИЕ

47.3 Два груза массы M1 и M2 подвешены на двух гибких нерастяжимых нитях, которые навернуты, как указано на рисунке, на барабаны, имеющие радиусы r1 и r2 и насаженные на общую ось; грузы движутся под влиянием силы тяжести. Определить угловое ускорение ε барабанов, пренебрегая их массами и массой нитей.
РЕШЕНИЕ

47.4 При условии предыдущей задачи определить угловое ускорение ε и натяжения T1 и T2 нитей, принимая во внимание массы барабанов, при следующих данных: M1=20 кг, M2=34 кг, r1=5 см, r2=10 см; массы барабанов: малого 4 кг и большого 8 кг. Массы барабанов считать равномерно распределенными по их внешним поверхностям.
РЕШЕНИЕ

47.5 К системе блоков, изображенной на рисунке, подвешены грузы: M1 массы 10 кг и M2 массы 8 кг. Определить ускорение w2 груза M2 и натяжение нити, пренебрегая массами блоков.
РЕШЕНИЕ

47.6 К нижнему шкиву C подъемника приложен вращающий момент M. Определить ускорение груза A массы M1, поднимаемого вверх, если масса противовеса B равна M2, а шкивы C и D радиуса r и массы M3 каждый представляют собой однородные цилиндры. Массой ремня пренебречь.
РЕШЕНИЕ

47.7 Вал кабестана механизма для передвижения грузов радиуса r приводится в движение постоянным вращающим моментом M, приложенным к рукоятке AB. Определить ускорение груза C массы m, если коэффициент трения скольжения груза о горизонтальную плоскость равен f. Массой каната и кабестана пренебречь.
РЕШЕНИЕ

47.8 Решить предыдущую задачу с учетом массы кабестана, момент инерции которого относительно оси вращения равен J.
РЕШЕНИЕ

47.9 Груз A массы M1, опускаясь по наклонной гладкой плоскости, расположенной под углом α к горизонту, приводит во вращение посредством нерастяжимой нити барабан B массы M2 и радиуса r. Определить угловое ускорение барабана, если считать барабан однородным круглым цилиндром. Массой неподвижного блока C и нити пренебречь.
РЕШЕНИЕ

47.10 Человек толкает тележку, приложив к ней горизонтальную силу F. Определить ускорение кузова тележки, если масса кузова равна M1, M2 масса каждого из четырех колес, r радиус колес, fк коэффициент трения качения. Колеса считать сплошными круглыми дисками, катящимися по рельсам без скольжения.
РЕШЕНИЕ

47.11 Каток A массы M1, скатываясь без скольжения по наклонной плоскости вниз, поднимает посредством нерастяжимой нити, переброшенной через блок B, груз C массы M2. При этом блок B вращается вокруг неподвижной оси O, перпендикулярной его плоскости. Каток A и блок B однородные круглые диски одинаковой массы и радиуса. Наклонная плоскость образует угол α с горизонтом. Определить ускорение оси катка. Массой нити пренебречь.
РЕШЕНИЕ

47.12 Груз B массы M1 приводит в движение цилиндрический каток A массы M2 и радиуса r при помощи нити, намотанной на каток. Определить ускорение груза B, если каток катится без скольжения, а коэффициент трения качения равен fк. Массой блока D пренебречь.
РЕШЕНИЕ

47.13 Стержень DE массы M1 лежит на трех катках A, B и C массы M2 каждый. К стержню приложена по горизонтали вправо сила F, приводящая в движение стержень и катки. Скольжение между стержнем и катками, а также между катками и горизонтальной плоскостью отсутствует. Найти ускорение стержня DE. Катки считать однородными круглыми цилиндрами.
РЕШЕНИЕ

47.14 Определить ускорение груза M2, рассмотренного в задаче 47.5, с учетом массы блоков сплошных однородных дисков массы 4 кг каждый.
РЕШЕНИЕ

47.15 Груз А массы M1, опускаясь вниз, посредством нерастяжимой нити, переброшенной через неподвижный блок D и намотанной на шкив B, заставляет вал C катиться без скольжения по горизонтальному рельсу. Шкив B радиуса R жестко насажен на вал C радиуса r; их общая масса равна M2, а радиус инерции относительно оси O, перпендикулярной плоскости рисунка, равен ρ. Найти ускорение груза A. Массой нити и блока пренебречь.
РЕШЕНИЕ

47.16 Центробежный регулятор вращается вокруг вертикальной оси с постоянной угловой скоростью ω. Определить угол отклонения ручек OA и OB от вертикали, принимая во внимание только массу M каждого из шаров и массу M1 муфты C, все стержни имеют одинаковую длину l.
РЕШЕНИЕ

47.17 Центробежный регулятор вращается с постоянной угловой скоростью ω. Найти зависимость между угловой скоростью регулятора и углом α отклонения его стержней от вертикали, если муфта массы M1 отжимается вниз пружиной, находящейся при α=0 в недеформированном состоянии и закрепленной верхним концом на оси регулятора; массы шаров равны M2, длина стержней равна l, оси подвеса стержней отстоят от оси регулятора на расстоянии a; массами стержней и пружины пренебречь. Коэффициент жесткости пружины равен c.
РЕШЕНИЕ

47.18 Центробежный пружинный регулятор состоит из двух грузов A и B массы M каждый, насаженных на скрепленный со шпинделем регулятора гладкий горизонтальный стержень муфты C массы M1, тяг длины l и пружин, отжимающих грузы к оси вращения; расстояние шарниров тяг от оси шпинделя равно e; c коэффициент жесткости пружин. Определить угловую скорость регулятора при угле раствора α, если при угле α0, где α0<α, пружины находятся в ненапряженном состоянии; массой тяг и трением пренебречь.
РЕШЕНИЕ

47.19 В регуляторе четыре груза одинаковой массы M1 находятся на концах двух равноплечих рычагов длины 2l, которые могут вращаться в плоскости регулятора вокруг конца шпинделя O и образуют с осью шпинделя переменный угол φ. В точке A, находящейся от конца шпинделя O на расстоянии OA=a, со шпинделем шарнирно соединены рычаги AB и AC длины a, которые в точках B и C в свою очередь сочленены со стержнями BD и CD длины a, несущими муфту D. В точках B и C имеются ползунки, скользящие вдоль рычагов, несущих грузы. Масса муфты равна M2. Регулятор вращается с постоянной угловой скоростью ω. Найти связь между углом и угловой скоростью ω в равновесном положении регулятора.
РЕШЕНИЕ