Решение задачи дирихле уравнения пуассона

Введение

Наиболее распространённым уравнением эллиптического типа является уравнение Пуассона.
К решению этого уравнения сводятся многие задачи математической физики, например задачи о стационарном распределении температуры в твердом теле, задачи диффузии, задачи о распределении электростатического поля в непроводящей среде при наличии электрических зарядов и многие другие.

Для решения эллиптических уравнений в случае нескольких измерений используют численные методы, позволяющие преобразовать дифференциальные уравнения или их системы в системы алгебраических уравнений. Точность решения опреде­ляется шагом координатной сетки, количеством итераций и разрядной сеткой компьютера [1]

Цель публикации получить решение уравнения Пуассона для граничных условий Дирихле и Неймана, исследовать сходимость релаксационного метода решения на примерах.

Уравнение Пуассона относится к уравнениям эллиптического типа и в одномерном случае имеет вид [1]:

(1)

где x – координата; u(x) – искомая функция; A(x), f(x) – некоторые непрерывные функции координаты.

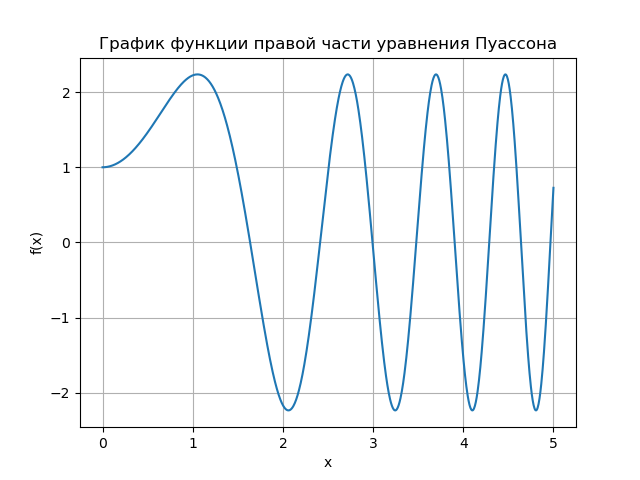
Решим одномерное уравнение Пуассона для случая А = 1, которое при этом принимает вид:

(2)

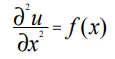
Зададим на отрезке [xmin, xmax] равномерную координатную сетку с шагом ∆х:

(3)

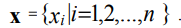
Граничные условия первого рода (условия Дирихле) для рассматривае­мой задачи могут быть представлены в виде:

(4)

где х1, xn – координаты граничных точек области [xmin, xmax]; g1, g2 – некоторые
константы.

Граничные условия второго рода (условия Неймана) для рассматривае­мой задачи могут быть представлены в виде:

(5)

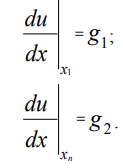
Проводя дискретизацию граничных условий Дирихле на равномерной координатной сетке (3) с использованием метода конечных разностей, по­лучим:

(6)

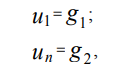
где u1, un – значения функции u(x) в точках x1, xn соответственно.

Проводя дискретизацию граничных условий Неймана на сетке (3), по­лучим:

(7)

Проводя дискретизацию уравнения (2) для внутренних точек сетки, по­лучим:

(8)

где ui, fi – значения функций u(x), f(x) в точке сетки с координатой xi.

Таким образом, в результате дискретизации получим систему линейных алгебраических уравнений размерностью n, содержащую n – 2 уравнения вида (8) для внутренних точек области и уравнения (6) и (7) для двух граничных точек [1].

Ниже приведен листинг на Python численного решения уравнения (2) с граничными условиями (4) – (5) на координатной сетке (3).

Разработанная мною на Python программа удобна для анализа граничных условий.Приведенный алгоритм решения на Python использует функцию Numpy — u=linalg.solve(a,b.T).T для решения системы алгебраических уравнений, что повышает быстродействие при квадратной матрице . Однако при росте числа измерений необходимо переходить к использованию трех диагональной матрицы решение для которой усложняется даже для очень простой задачи, вот нашёл на форуме такой пример:

Программа численного решения на равномерной по каждому направлению сетки задачи Дирихле для уравнения конвекции-диффузии

(9)

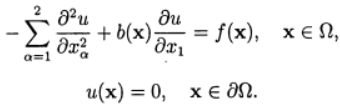
Используем аппроксимации центральными разностями для конвективного слагаемого и итерационный метод релаксации.для зависимость скорости сходимости от параметра релаксации при численном решении задачи с /(х) = 1 и 6(х) = 0,10. В сеточной задаче:

(10)

Представим матрицу А в виде суммы диагональной, нижней треугольной и верхней треугольных матриц:

(10)

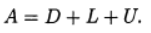
Метод релаксации соответствует использованию итерационного метода:

(11)

При говорят о верхней релаксации, при — о нижней релаксации.

На графике показана зависимость числа итераций от параметра релаксации для уравнения Пуассона (b(х) = 0) и уравнения конвекции-диффузии (b(х) = 10). Для сеточного уравнения Пуассона оптимальное значении параметра релаксации находится аналитически, а итерационный метод сходиться при .

1. Приведено решение эллиптической задачи на Python с гибкой системой установки граничных условий
2. Показано что метод релаксации имеет оптимальный диапазон () параметра релаксации.

Ссылки:

1. Рындин Е.А. Методы решения задач математической физики. – Таганрог:
   Изд-во ТРТУ, 2003. – 120 с.
2. Вабищевич П.Н.Численные методы: Вычислительный практикум. — М.: Книжный дом
   «ЛИБРОКОМ», 2010. — 320 с.

Видео:7.2 Задача 1. Краевая задача для уравнения ПуассонаСкачать

Решение задачи Дирихле для уравнения Пуассона в многомерном бесконечном слое Текст научной статьи по специальности « Математика»

Видео:9. Уравнение ПуассонаСкачать

Аннотация научной статьи по математике, автор научной работы — Алгазин О.Д., Копаев А.В.

В работе методом преобразования Фурье решается краевая задача Дирихле для уравнения Пуассона в области, ограниченной двумя параллельными гиперплоскостями в R^n. Решение представлено в виде суммы интегралов, ядра которых найдены в конечном виде. В частности построена функция Грина оператора Лапласа для задачи Дирихле , через которую записывается решение задачи. В случае если заданные граничные значения являются обобщенными функциями медленного роста , решение задачи Дирихле для однородного уравнения (Лапласа) записывается в виде свертки ядер с этими функциями. DOI: 10.7463/mathm.0415.0812943

Видео:Задача Дирихле для круга. Уравнение ЛапласаСкачать

Похожие темы научных работ по математике , автор научной работы — Алгазин О.Д., Копаев А.В.

Видео:7.6 Задача 5. Краевая задача для уравнения ПуассонаСкачать

Текст научной работы на тему «Решение задачи Дирихле для уравнения Пуассона в многомерном бесконечном слое»

Математика к Математическое

Ссылка на статью:

// Математика и Математическое моделирование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2015. № 4. С. 41-53.

Представлена в редакцию: 17.09.2015

© МГТУ им. Н.Э. Баумана

Решение задачи Дирихле для уравнения Пуассона в многомерном бесконечном слое

Алгазин О. Д.1’*, Копаев А. В.1 * mopi66@yandex.ru

1МГТУ им. Н.Э. Баумана, Москва, Россия

В работе методом преобразования Фурье решается краевая задача Дирихле для уравнения Пуассона в области, ограниченной двумя параллельными гиперплоскостями в Rлn. Решение представлено в виде суммы интегралов, ядра которых найдены в конечном виде. В частности построена функция Грина оператора Лапласа для задачи Дирихле, через которую записывается решение задачи. В случае если заданные граничные значения являются обобщенными функциями медленного роста, решение задачи Дирихле для однородного уравнения (Лапласа) записывается в виде свертки ядер с этими функциями.

Ключевые слова: преобразование Фурье; функция Грина; задача Дирихле; уравнение Пуассона; обобщенные функции медленного роста.

Двух — и трёхмерное уравнение Пуассона описывает многие стационарные процессы при наличии источников (стоков) в различных областях механики и физики. Например, в теории тепло- и массопереноса, гидро- и аэромеханике, электростатике и т.д. Поэтому поиск точных решений краевых задач для уравнения Пуассона в различных областях является весьма актуальным. Известные точные решения краевых задач для линейных уравнений в частных производных содержатся в справочнике [1].

В данной статье найдено точное решение задачи Дирихле для уравнения Пуассона в многомерном бесконечном слое. Для п-мерного полупространства основным методом решения краевых задач для линейных уравнений в частных производных с постоянными коэффициентами является преобразование Фурье по переменным в граничной гиперплоскости [2]. Этот же метод применим и для бесконечного слоя, что и делается в нашей работе. Для полосы и бесконечного слоя в трёхмерном пространстве решения этой задачи известны [1]. Причем в трехмерном случае функция Грина записывается в виде бесконечного ряда. Для бесконечного слоя в и-мерном пространстве задача Дирихле для уравнения Лапласа решалась одним из авторов другим методом в работе [3]. Решение смешанной

краевой задачи Дирихле — Неймана для уравнения Лапласа в бесконечном слое п-мерного пространства методом преобразования Фурье см. в нашей работе [4]. В настоящей работе решение получено в интегральной форме и ядра интегралов выражены в конечном виде через элементарные функции и функции Бесселя. При этом получено рекуррентное соотношение, связывающее ядра интегралов для и-мерного и (и+2)-мерного слоев. Уже для трехмерного случая получены новые формулы по сравнению с известными [1].

1.Обозначения и постановка задачи

Введём следующие обозначения:

х = (х1. хп) е !п , (х, у) — (х1. хп,у) е Еп+1 , уеЕ ,

Ли(х, у) — Ли — иХ1Х1 + —Ь ихпхп + иуу — оператор Лапласа.

р(г)= пгт— [ Г(х)е1хЫг —

преобразование Фурье суммируемой функции /(х). Если суммируемая по х функция [(х, у) зависит от переменных х и у, то ее преобразование Фурье по х будем обозначать

Аналогично определяется обратное преобразование Фурье суммируемой функции

!(х) — Т-1[Р](х) — —П- [ Р(1)е-^й1 и суммируемой по t функции Р(1, у)

Г—1[Р](х,У) — тг1- [ %у)е-1х’й1.

Определение преобразования Фурье обобщенных функций медленного роста см. [5].

Рассмотрим задачу Дирихле для уравнения Пуассона (неоднородного уравнения Лапласа):

Ли(х, у) — /(х, у) , х еШп , 0 0,

22) I Кп(х, у) dx =—> 1 при у ^ +0 ,

3) для V5 >0 , lim sup Кп(х, у) = 0.

Эти свойства означают, что Кп(х, у) является аппроксимативной единицей или 5 —образной системой функций от х (с параметром у ), при у ^ +0 , Кп(х, у) слабо сходится к 5 — функции 5(х). Поскольку

Ln (х, У) = Кп (х, а — у) ,

то Ln (х, у) является аппроксимативной единицей при у ^ а — 0 .

Поэтому, если ф(х) Е S'(Rn) и ф(х) Е S'(Rn), то формула (1) дает обобщенное решение задачи Дирихле для уравнения Лапласа:

lim v(x,у) = ф(х) в S’ , lim v (х,у) = ф(х) в S’.

Если ф(х) и ф(х) обычные функции полиномиального роста, то в каждой точке непрерывности

lim v(x, у) = ф(х), lim v (х, у) = ф(х) .

3. Решение неоднородного уравнения с однородными краевыми условиями

ау/(х,у) = /(х,у) , хе1п , 0 Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Правую часть уравнения Пуассона также разложим в ряд Фурье

Подставив ряды в уравнение Пуассона и приравняв коэффициенты, получим

Ьк (t) = -П2к2 +a2t2 ‘ k = 1’2’3’- И

Применив обратное преобразование Фурье, получим решение краевой задачи

2 V-1 ( Га пкт ) пку

w(x,у) = — У Мпк(х) * I /(х,т) sin-dr;- sin-=

Г f 2^ nkï nky = —I I f(t,T) / Mnk (x — t) sin-sin-dtdx ,

Jo J-œ rk=1 a a J

1yn2k2 + ^^ 2 Га пкт

т) sin —dT = T-1[fk(t)](x).

Если правая часть уравнения Пуассона равна дельта—функции, f(x, у) = S(x — x0, у — у0)= 5(х — х0)5(у — у0), х0 ЕШП , 0 Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Если ф(х) и ф(х) — обычные функции полиномиального роста, то решение задачи Дирихле для уравнения Лапласа записывается интегральной формулой

— I мом! ^ЦрШх — фйр .

Функцию Грина получим, просуммировав ряд

М2к (х) = Т-1[ш 2 ¡с ](х)= Т-1 с2

п2к2 + a2t2 1 fm а2 1 (пк

= 2nJ0 ж2к2 + а2 р2 р]о(рх1)dp = 2ÜЧт W) ‘

= ^ jm ^exp (—пх — Х0 ch(О/а) — cos (п(у — у 0)/а) 4па J0 ch (пх — x0ch(E;

— exp (—пх — Х0 ch(О/а) — cos (п(у + У0)/а) ch (пх — Х0 ch(О/а) — cos (п(у + у0)/а)

Легко проверить, что

sinh(7rx — t ch(^) /a)

т=0 2 a2 J0 (ch(nx — tch(%)/a) — cos (лу/а))2 s h (p( a — y))

sh ( p) sinh( — ch( ) / )

(ch( — ch( )/ ) + cos ( / ))2

И решение задачи Дирихле для уравнения Пуассона в трехмерном бесконечном слое может быть записано в виде

+ j j f (t,T) G2(x,y,t,r) dtdx,

G (x tT) = _L f™ [exp -11 ch(o/g) -cos fro — T)/a)

2 x, у, , т 4^aJ0 | ch (л»|х — t| ch(^)/a) — cos (п(у — т)/а)

exp (—л»|х — t| ch(^)/a) — cos (n(y + т)/а)

ch (л»|х — t| ch(^)/a) — cos (n(y + т)/а) В частности для решения задачи Дирихле для уравнения Лапласа в трехмерном бесконечном слое получается формула другого вида

■f^(t) dtf 2U Ju2 Jo

sin(rcy/a) f г^ f™ sinh(rc|x — t| ch(^) /a)

J0 (ch(rc|x — t| ch(^)/a) — cos (ny/a)

sinh(rc|x — t| ch(^) /a) (ch(rc|x — t| ch(^)/a) + cos (ny/a))2 ‘

■ f 4>(t) dt f Ju2 Jo

6. Решение задачи Дирихле для бесконечного слоя в пространстве произвольной размерности

Для пространства произвольной размерности п решение задачи Дирихле для уравнения Пуассона в слое записывается с помощью функции Грина в следующем виде

+ I I f(t, t) Gn-1(x, y, t, t) dtdx ,

где в случае четной размерности п = 2к

G21C-1&,У, t, «0 = G*^k-i(x — t|,у,т) = G*2k-i(r,у,т) =

1 ch(nr/a) — cos(n(y — т)) — ln

4п ch(nr/a) — cos(n(y — т))

= K2k-1dx —1|, у) = к;к-1(г, у) =

(—1)к-1 /1 дк-1( 1 sin(rcy/a)

(2п)к-1 r дг) 2а ch(nr/a) — cos(ny/a)J ,

= L2k-1(x — tl У) = L*2k-1(r, У) = sin(rcy/a)

(2п)к 1 г дг) 2а ch(nr/a) + cos(ny/a)J’ В случае нечетной размерности п = 2к + 1

G2k (х, У, t, т) = G*2k (|х — t|, у, т) = G*2k (г, у, т) =

-1 /1 дк Ч 1 Гт rexp (—nr ch(f)/a) — cos (n(y — x)/a) (2n)k-1 r dr) 4naJ0 ch (nr ch(^)/a) — cos (л(у — т)/а) exp (—nr ch(^)/a) — cos (n(y + т)/а))

ch (nr ch(^)/a) — cos (n(y + r)/a)

2а2 ]п (сЪ(пг сЪ(%)/а) — соз (пу/а))2 = V*2к (|Х — г, У) = 1*2к (г, У) =

(сЪ(пг сЪ(%)/а) + соз (пу/а))2

Например, для бесконечного слоя в четырёхмерном пространстве имеем

1 д 1 д ( 1 зп(пу/а)

К3(х, у) = — — — Ыг, У) = — — У’ *

2пгдг2а сЬ(пг/а) — соз(пу/а)/ зт(пу/а) зЪ(пг/а)

4а2 г(сЪ(пг/а) — соз(пу/а))2 1 зп(пу/а) зЬ(пх/а)

4а2 х(сЬ(пх/а) — соз(пу/а))2 зт(пу/а)зЪ(пх/а) ГГ

4а2 х(сЪ(пх/а) + соз(пу/а))2

вз(х, у, хо, Уо) = С;(г, у, уо) = —

сЬ(пг/а) — соз(п(у — уо))

4п сЪ(пг/а) — соз(п(у — у0)) зЪ(пг/а) зт(пу/а) зт (пу0/а)

4паг (сЬ(пг/а) — соз(п(у + у0)/а))(сЬ(пг/а) — соз(п(у — у0)/а))’ где г = х — Хо.

Легко проверить, что

И решение задачи Дирихле для уравнения Пуассона в четырехмерном бесконечном слое может быть записано в виде

+ I I /(^, т) С3(х, у, t, т) й1йт,

1 зЪ(пг/а) зп(пу/а) зп(пт/а)

4паг (сЪ(пг/а) — соз(ж(у + т)/а))(сЪ(пг/а) — соз(ж(у — т)/а)) ‘

В частности для решения задачи Дирихле для уравнения Лапласа в четырехмерном бесконечном слое получается формула

sin(ny/a) Г ф(0 sh(nx — t/a)dt

v(x,у) х — t(ch(nx — t/a) — cos(ny/a))2 +

sin(rcy/a) f ^>(t) sh(rcx — t/a)dt

4a2 JU3 x — t(ch(nx — t/a) + cos(ny/a))2 ‘

Отметим, что полученные формулы для решения задачи Дирихле для уравнения Лапласа в бесконечном слое применимы и в том случае, когда граничные значения являются обобщенными функциями медленного роста. В этом случае решение является обобщенным: v(x, у) при у — +0 и у — а — 0 слабо сходится в £'(ЕП) к заданным граничным значениям. В случае трех переменных функция Грина получена в виде однократного интеграла.

1. Полянин А.Д. Справочник по линейным уравнениям математической физики. М.: Физматлит, 2001.576 с.

2. Комеч А.И. Линейные уравнения в частных производных с постоянными коэффициентами // Итоги науки и техники. Сер. Современные проблемы математики: Фундаментальные направления. 1988. т. 31. с. 127-261.

3. Касьянов Е.Ю., Копаев А.В. О решении задачи Дирихле для некоторых многомерных областей методом воспроизводящих ядер // Известия вузов. Математика. 1991. №6. с. 17-20.

4. Алгазин О.Д., Копаев А.В. Решение смешанной краевой задачи для уравнения Лапласа в многомерном бесконечном слое // Вестник МГТУ им. Н.Э.Баумана. Сер. Естественные науки. 2015. №1. с. 3-13.

5. Владимиров В.С. Обобщенные функции в математической физике. М.: Наука, 1979. 320 с.

6. Бохнер С. Лекции об интегралах Фурье. М.: Физматгиз, 1962. 360 с.

7. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Изд-во МГУ, 1999. 798 с.

8. Диткин В.А., Прудников А.П. Интегральные преобразования и операционное исчисление. М.: Физматгиз, 1961. 524 с.

9. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Наука, 1971. 1108 с.

Mathematics and Mathematical Madelling of the Bauman MSTU, 2015, no. 4, pp. 41-53.

Mathematics & Mathematical Modelling

Electronic journal of the Bauman MSTU

© Bauman Moscow State Technical Unversity

Solution of the Dirichlet Problem for the Poisson’s Equation in a Multidimensional Infinite Layer

Algazin O. D.1*, Kopaev A. V.1

:Bauman Moscow State Technical University, Moscow, Russia

Keywords: Fourier transform, Green function, Dirichlet boundary value problem, Poisson equation,

The paper considers the multidimensional Poisson equation in the domain bounded by two parallel hyperplanes (in the multidimensional infinite layer). For an n-dimensional half-space method of solving boundary value problems for linear partial differential equations with constant coefficients is a Fourier transform to the variables in the boundary hyperplane. The same method can be used for an infinite layer, as is done in this paper in the case of the Dirichlet problem for the Poisson equation. For strip and infinite layer in three-dimensional space the solutions of this problem are known. And in the three-dimensional case Green’s function is written as an infinite series. In this paper, the solution is obtained in the integral form and kernels of integrals are expressed in a finite form in terms of elementary functions and Bessel functions. A recurrence relation between the kernels of integrals for n-dimensional and (n + 2) -dimensional layers was obtained. In particular, is built the Green’s function of the Laplace operator for the Dirichlet problem, through which the solution of the problem is recorded. Even in three-dimensional case we obtained new formula compared to the known. It is shown that the kernel of the integral representation of the solution of the Dirichlet problem for a homogeneous Poisson equation (Laplace equation) is an approximate identity (S-shaped system of functions). Therefore, if the boundary values are generalized functions of slow growth, the solution of the Dirichlet problem for the homogeneous equation (Laplace) is written as a convolution of kernels with these functions.

1. Polyanin A.D. Spravochnik po linejnym uravnenijam matematicheskoj fiziki [Handbook of linear equations of mathematical physics]. Moscow, Fizmatlit publ., 2001. 576 p. (in Russian).

2. Komech A.I. Linear partial differential equations with constant coefficients. Itogi nauki i tehniki. Ser. Sovremennye problemy matematiki: Fundamental’nye napravlenija [The results of science and technology. Ser. Contemporary Mathematics: Fundamental Directions], 1988, vol. 31, pp. 127-261. (in Russian).

3. Kas’janov E.JU., Kopaev A.V. On a solution of the Dirichlet’s Problem for a certain multidimensional domains by means of the reproducing kernels method. Izvestija vuzov. Matematika = Proceedings of the higher educational institutions. Mathematics, 1991, №6, pp. 17-20. (in Russian).

4. Algazin O.D., Kopaev A.V. Solution to the mixed boundary-value problem for Laplace equation in multidimentional infinite layer. Vestnik MGTU im. N.E. Baumana. Ser. Estestvennye nauki = Herald of the Bauman MSTU. Ser. Natural Sciences, 2015, №1, pp. 313. (in Russian).

5. Vladimirov V.S. Obobshchennye funktsii v matematicheskoj fizike [Generalized functions in mathematical physics]. Moscow, Nauka publ., 1979, 320 p. (in Russian).

6. Bokhner S. Lektsii ob integralah Fur’e [Lectures on Fourier integrals]. 1962, 360 p. (in Russian).

💡 Видео

УМФ, 01.12, решение задач Лапласа и Пуассона в случае неоднородных граничных условийСкачать

Шапошникова Т. А. - Уравнения с частными производными - Вариационный метод решения задачи ДирихлеСкачать

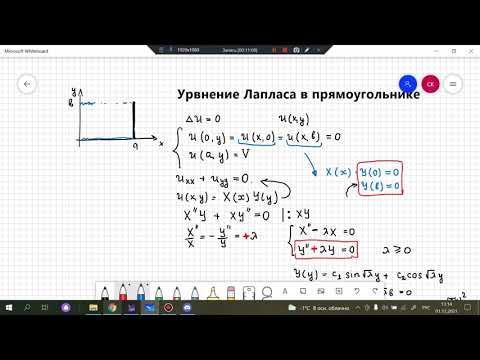
7.5 Задача 4. Краевая задача для уравнения ПуассонаСкачать

Уравнения математической физики 15+16 Задача Дирихле для уравнения Лапласа - Пуассона в кругеСкачать

6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольцеСкачать

7.8 Задача 7. Краевая задача для уравнения ПуассонаСкачать

7.9 Задача 8. Краевая задача для уравнения ПуассонаСкачать

Уравнение Пуассона и задача ДирихлеСкачать

7.3 Задача 2. Краевая задача для уравнения ПуассонаСкачать

Практическое занятие. Численное решение уравнений Лапласа и ПуассонаСкачать

29. Адиабатический процесс. Уравнение ПуассонаСкачать

Краевая задача для уравнений Лапласа и Пуассона на R^2Скачать

Задача Дирихле и НейманаСкачать

OTAROVA JAMILA МЕТОД ФУРЬЕ РЕШЕНИЯ ЗАДАЧИ ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕСкачать

ЧК_МИФ_3_1_2_5 (L3) УРАВНЕНИЕ ПУАССОНАСкачать

7.4 Задача 3. Краевая задача для уравнения ПуассонаСкачать