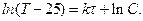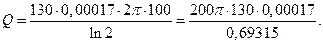Решение задач составление дифференциальных уравнений

Теперь, когда вы научились находить производные и интегралы, самое время перейти к более сложной теме: решению дифференциальных уравнений (они же дифуры, диффуры и диф.уры :)), то есть уравнений, которые вместе с самой функцией (и/или аргументом), содержат и производную или даже несколько.

Как же решать дифференциальные уравнения? Главное, что понадобится, это а) умение правильно определить тип дифференциального уравнения и б) умение хорошо интегрировать — это существенная часть работы. А дальше следовать алгоримам для каждого из типов уравнений, которые подробно описаны в учебниках и ниже в примерах.

В этом разделе вы найдете решенные задачи на составление и решение дифференциальных уравнений. Примеры решений дифуров выложены бесплатно для вашего удобства и отсортированы по темам — изучайте, ищите похожие, решайте свои. Есть трудности в выполнении заданий? Мы готовы оказать помощь по дифференциальным уравнениям

Видео:Разностные уравнения | Решение задачСкачать

Как решить дифференциальное уравнение онлайн?

Да ладно, неужели только вручную? Мучиться, определять тип, переносить, интегрировать, заменять, снова интегрировать, подставлять, выводить? Наверняка ведь есть онлайн-калькуляторы, которые позволяют решать дифференциальные уравнения?

У меня две новости, хорошая и плохая. Хорошая в том, что действительно самые распространенные типы дифференциальных уравнений математические программы умеют решать. Плохая в том, что обычно они выводят ответ (для научных расчетов этого достаточно), а не полное решение.

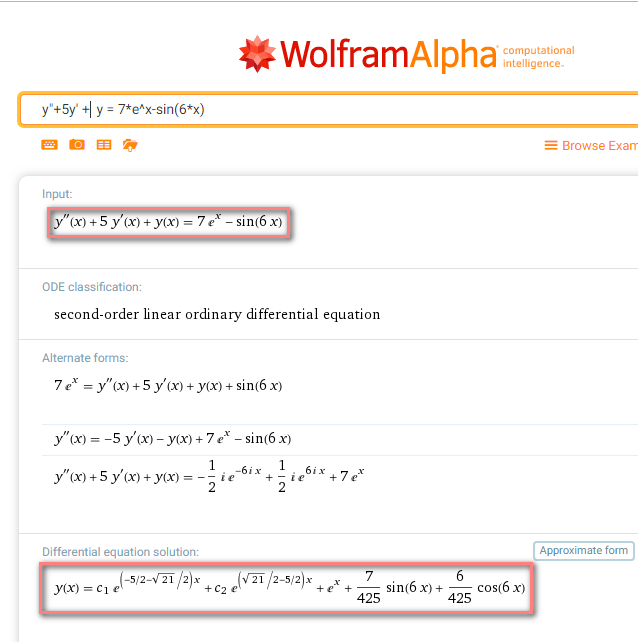
Есть известный математический сервис www.wolframalpha.com, которые представляет полные решения множества математических задач, в том числе диффуров онлайн (на английском языке) за 7 долларов в месяц. Ответы же доступны всем и могут помочь проверять правильность своего решения (см. ниже на скриншоте обведено само уравнение и его решение). Подробнее об этом сайте и типичных задачах, решаемых на нем, вы можете узнать тут.

Если вы забьете в поисковик что-то вроде «решить дифференциальное уравнение онлайн», то получите десятки ссылок на сайты, обещающие именно это.

Я проверила все сайты с первых страниц Яндекса и Гугла. Большая часть сайтов использует результаты расчетов www.wolframalpha.com (см. выше) и показывает вам ответ (и рекламу :)). Некоторые при этом не показывают даже ответа или говорят, что уравнение введено некорректно (хотя это вполне стандартное решаемое вручную линейное уравнение с постоянными коэффициентами). Полное решение не выдал ни один сайт.

Выводы? Бесплатно и полно и онлайн — не бывает. Хотите получать полные решения — используйте платную подписку на ВольфрамАльфа (или проконсультируйтесь у нас). Хотите ответы — там же бесплатно. Хотите научиться решать? Придется засучить рукава. Примеры на этой странице и ссылки внизу помогут вам. Удачи!

Видео:Дифференциальные уравнения: задача 3Скачать

Общий интеграл, семейство кривых

Задача 1. Показать, что функция $y^2-x^2-Cy=0$ является общим интегралом дифференциального уравнения $y'(x^2+y^2)-2xy=0.$

Задача 2. Составить дифференциальное уравнение семейства кривых $C_1 x+(y-C_2)^2=0.$

Видео:Решение физических задач с помощью дифференциальных уравненийСкачать

Решения дифференциальных уравнений 1 порядка

Задача 3. Найти общее решение линейного дифференциального уравнения первого порядка $ xy’+x^2+xy-y=0.$

Задача 4. Решить однородное дифференциальное уравнение $y’=-y/x quad (x ne 0).$

Задача 5. Решить дифференциальное уравнение $(y^4-2x^3y)dx+(x^4-2xy^3)dy=0.$

Задача 6. Решить однородное дифференциальное уравнение $(2x+y+1)dx+(x+2y-1)dy=0.$

Задача 7. Решить линейное дифференциальное уравнение первого порядка $y’-2xy=3x^2-2x^4.$

Задача 8. Решить дифференциальное уравнение $(x+y^2)y’=y-1.$

Видео:Задачи приводящие к дифференциальным уравнениям.Скачать

Решение задачи Коши для ДУ

Задача 9. Решить дифференциальное уравнение с разделяющимися переменными $(1+x^2)dy-2xydx=0.$ Найти частное решение, удовлетворяющее начальному условию $y(0)=1$.

Задача 10. Решить задачу Коши для дифференциального уравнения второго порядка $2y y» +1 =(y’)^2, , y(1/3)=1, , y'(1/3)=2$.

Задача 11. Найти решение задачи Коши для дифференциального уравнения $$ y’= frac, y(1)=1. $$

Задача 12. Решить задачу Коши для дифференциального уравнения третьего порядка $$ y»’=x+cos x, quad y(0)=0, y'(0)=0, y»(0)=0. $$

Видео:Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

Решения дифференциальных уравнений 2 порядка

Задача 13. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами $y»+4y’+4y=xe^.$

Задача 14. Решить задачу Коши для дифференциального уравнения второго порядка с постоянными коэффициентами методом вариации: $$ y»-3y’=frac<9e^><3+e^>, quad y(0)=4ln 4, y'(0)=3(3ln 4-1). $$

Видео:Задача на составление дифференциального уравненияСкачать

Cоставление дифференциальных уравнений

Задача 15. Скорость остывания нагретого тела пропорциональна разности температур тела и окружающей среды. За 10 минут тело охладилось от 100 до 60 градусов. Температура среды постоянна и равна 20 градусам. Когда тело остынет до 25 градусов?

Задача 16. Моторная лодка движется в спокойной воде со скоростью 5 м/сек. На полном ходу ее мотор выключается и через 40 сек после этого скорость лодки уменьшается до 2 м/сек. Определить скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости движения лодки.

Видео:Дифференциальные уравнения: задача 2Скачать

Решения нелинейных дифференциальных уравнений

Задача 17. Решить дифференциальное уравнение $y^2 ^2 -2xyy’+2y^2-x^2=0.$

Задача 18. Решить дифференциальное уравнение $^2-4xyy’+8y^2=0.$

Видео:Задача на составление Дифференциального уравненияСкачать

III. Задачи на составление дифференциальных уравнений

Методика составления и решения прикладных задач теории обыкновенных дифференциальных уравнений

Составление дифференциального уравнения по условию за­дачи (механической, физической, химической или технической) состоит в определении математической зависимости между пе­ременными величинами и их приращениями.

В ряде случаев дифференциальное уравнение получается без рассмотрения приращений — за счет их предварительного учета. Например, представляя скорость выражением , мы не привлекаем приращений ∆s и ∆t, хотя они фактически учтены в силу того, что

.

Ускорение в какой-нибудь момент времени t выражается зависимостью:

.

При составлении дифференциальных уравнений приращения сразу же заменяются соответствующими дифференциалами. Изучение любого процесса сводится:

1) к определению его отдельных моментов;

2) к установлению общего закона его хода.

Отдельный момент процесса (т. н. элементарный процесс) выражается уравнением, связывающим переменные величины процесса с их дифференциалами или производными — диффе­ренциальным уравнением; закон общего хода процесса выра­жается уравнением, связывающим переменные величины про­цесса, но уже без дифференциалов этих величии.

Исчерпывающих правил для составления дифференциальных уравнений нет. В большинстве случаев методика решения техни­ческих задач с применением теории обыкновенных дифферен­циальных уравнений сводится к следующему:

1.Подробный разбор условий задачи и составление чертежа, поясняющего ее суть.

2.Составление дифференциального уравнения рассматривае­мого процесса.

3.Интегрирование составленного дифференциального уравне­ния и определение общего решения этого уравнения.

4.Определение частного решения задачи на основании дан­ных начальных условий.

5.Определение, по мере необходимости, вспомогательных пара­
метров (например, коэффициента пропорциональности и др.),
используя для этой цели дополнительные условия задачи.

6. Вывод общего закона рассматриваемого процесса и число­
вое определение искомых величии.

7. Анализ ответа и проверка исходного положения задачи.
Некоторые из этих рекомендаций в зависимости от характера
задачи могут отсутствовать.

Как и при составлении алгебраических уравнений, при реше­нии прикладных задач по дифференциальным уравнениям многое зависит от навыков, приобретаемых упражнением. Однако здесь еще в большей степени требуется изобретательность и глубокое понимание сути изучаемых процессов.

Рассмотрим процесс решения следующих задач:

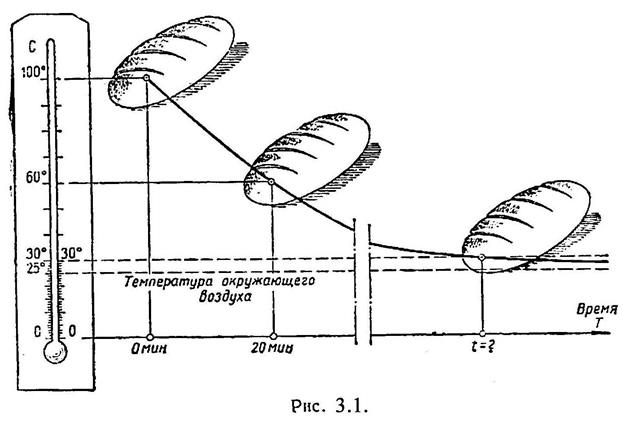
Температура вынутого из печи хлеба в течение 20 мин. падает от 100 0 до 60 0 (рис. 3.1). Температура воздуха равна 25 0 . Через сколько времени от момента начала охлаждения температура хлеба понизится до 30 0 ?

Решение:

В силу закона Ньютона скорость охлаждения тела пропорциональна разности температур тела и окружающей среды. Это – процесс неравномерный. С изменением разности температур в течение процесса меняется также и скорость охлаждения тела. Дифференциальное уравнение охлаждения хлеба будет:

.

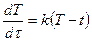
где Т – температура хлеба;

t – температура окружающего воздуха ( в нашем случае 25 0 );

k – коэффициент пропорциональности;

— скорость охлаждения хлеба.

Пусть — время охлаждения.

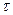
Тогда, разделяя переменные, получим:

,

или для условий данной задачи :

.

Потенцируя обе части последнего равенства, имеем:

,

. (1)

Произвольную постоянную С определяем, исходя из начального условия: при мин, Т=100 о .

или С=75.

Величину 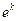определяем, исходя из данного дополнительного условия: при мин, Т=60 о .

и .

Таким образом, уравнение охлаждения хлеба при условиях нашей задачи примет вид:

. (2)

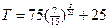
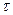
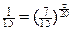
Из уравнения (2) легко определяем искомое время при температуре хлеба Т=30 о :

, или.

мин.

Итак, после 1 часа 11 мин. Хлеб охлаждается до температуры 30 о С.

Задача 3.2. Трубопровод тепловой магистрали (диаметр 20 см) защищен изоляцией толщиной 10 см; величина коэффициента теплопроводности k=1,00017. Температура трубы 160о; температура внешнего покрова 30о (рис.8). Найти распределение температуры внутри изоляции, а также количество теплоты, отдаваемого одним погонным метром трубы.

Решение. Если тело находится в стационарном тепловом состоянии и температура Т в каждой его точке есть функция только одной координаты х, то согласно закону теплопроводности Фурье количество теплоты, испускаемое в секунду:

, (1)

где F(x)- площадь сечения тела на расстоянии х,

k – коэффициент теплопроводности.

Здесь (2)

где l – длина трубы в см,

х – радиус трубопровода в см.

Таким образом, после разделения переменных дифференциальное уравнение примет вид:

(3)

Интегрируя обе части равенства (3), находим:

или 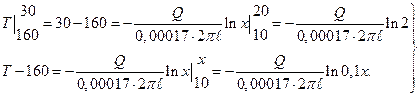(4)

Разделив почленно уравнения второе на первое, получим:

.

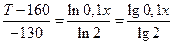
Отсюда закон распределения температуры внутри изоляции:

.

Из первого уравнения системы(4) при =100 см имеем:

Количество теплоты, отдаваемое в течение суток, равно

кал.

Видео:Задача на составление уравнения движения системыСкачать

Урок по теме «Составление дифференциальных уравнений»

Разделы: Математика

Цель урока:

1. Научить составлять дифференциальное уравнение некоторого явления. Закрепить навык решения дифференциального уравнения.
2. Развивать мышление и речь учащихся.

1. Повторить:

а) Какое уравнение называется дифференциальным?
б) Что значит решить дифференциальное уравнение?
в) Что называется решением дифференциального уравнения?
г) Какие способы решения дифференциального уравнения вам известны?

2. а) N 21. (Виленкин Н.Я. “Алгебра и математический анализ” )

y=f(x) – функция, (x;y) – координаты точки касания.

Точка пересечения касательной с осью Оx:

Абсцисса точки пересечения касательной с осью Оу равна 0.

Так как точка (х;у)- середина отрезка, абсциссы концов которого

В комнате, где температура 20 0 С , некоторое тело остыло за 20 мин. от 100 0 до 60 0 С. Найдите закон охлаждения тела; через сколько минут оно остынет до 30 0 С?

Повышением температуры в комнате пренебречь.

Решение: В силу закона Ньютона (скорость охлаждения пропорциональна разности температур тела и охлаждающей среды) можем записать:

в) Криминалисты, прибыв на место преступление, обнаружили труп человека, температура тела которого была 27 0 . Через один час температура трупа стала 25 0 . Температура окружающего воздуха 16 0 . Считая, что в момент убийства человек имел температуру тела 37 0 , определите промежуток времени между моментом убийства человека и моментом обнаружения его тела.

г) Напишите уравнение кривой, проходящей через точку В(3;1), для которой отрезок касательной между точкой касания и осью Ох делится пополам в точке пересечения с осью Оу.

📺 Видео

ФП1. Решение текстовых задач на составление дифференциальных уравненийСкачать

Решение задачи Коши дифференциального уравнения #maths #calculus #differentialequation #algebraСкачать

Диффуры на выживание | Дифференциальные уравненияСкачать

Составление дифференциального уравненияСкачать

Операторный метод решения дифференциальных уравнений | Решение задачСкачать

5 Численное решение дифференциальных уравнений Part 1Скачать

Решение физических задач при помощи диффуров | Дифференциальные уравненияСкачать

Особые решения дифференциальных уравнений, огибающая семейства кривых | Лекция 34 | МатанализСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Остров Диффуров: где капитан Флинт спрятал уравнение Клеро? | Дифференциальные уравненияСкачать