- Задание разного уровня сложности по теме : «Системы уравнений в задачах на скорость». учебно-методический материал
- Скачать:
- Предварительный просмотр:
- Решение текстовых задач. 9-й класс
- Решение задач на движение с помощью систем линейных уравнений
- Просмотр содержимого документа «Решение задач на движение с помощью систем линейных уравнений»
- 📽️ Видео
Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать
Задание разного уровня сложности по теме : «Системы уравнений в задачах на скорость».
учебно-методический материал
Задание разного уровня сложности по теме : «Системы уравнений в задачах на скорость».
Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать
Скачать:
| Вложение | Размер |
|---|---|
| Задание разного уровня сложности по теме : «Системы уравнений в задачах на скорость». | 15.72 КБ |
Видео:Задачи на движение | Математика TutorOnlineСкачать
Предварительный просмотр:
Задание разного уровня сложности по теме : «Системы уравнений в задачах на скорость».
1 уровень сложности
2 уровень сложности
3 уровень сложности
Из двух городов, расстояние между которыми 700 км, одновременно навстречу друг другу отправляются два поезда и встречаются через 5 часов.
Если второй поезд отправится на 7 ч раньше первого, то они встретятся через 2 ч после отправления первого поезда. Найдите скорость каждого поезда.
Из двух городов, расстояние между которыми 700 км, одновременно навстречу друг другу отправляются два поезда и встречаются через 5 часов.
Если второй поезд отправится на 7 ч раньше первого, то они встретятся через 2 ч после отправления первого поезда. Найдите скорость каждого поезда.
Из двух городов, расстояние между которыми 700 км, одновременно навстречу друг другу отправляются два поезда и встречаются через 5 часов.
Если второй поезд отправится на 7 ч раньше первого, то они встретятся через 2 ч после отправления первого поезда. Найдите скорость каждого поезда.
Дополни недостающие элементы решения задачи:
Видео:Урок по теме РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ 7 КЛАСССкачать
Решение текстовых задач. 9-й класс
Разделы: Математика
Класс: 9
- Совершенствование навыков решения текстовых задач.
- Продолжить формирование знаний учащихся по решению систем уравнений с двумя неизвестными.
- Развитие математической грамотности.
1. Актуализация знаний учащихся (5 минут).
1. Найдите решение системы уравнений:
Ответы: 1) (1;3); 2) (0;3); 3) (1;2); 4) (2;1).
2. Выразите из уравнения 3х + 2у = 5 переменную х через переменную у.
1) 
2) 
2. Объяснение нового материала (8 минут).
Алгоритм решения задач на движение и на производительность:
- Ввести неизвестные величины.
- Составить краткую запись задачи в таблице (скорость, путь, время) или (производительность, работа, время).
- Исходя из условия задачи, составить систему двух уравнений с двумя неизвестными.
- Решить систему уравнений, исключив те корни, которые не подходят по условию задачи.
- Записать ответ по вопросу задачи.
Расстояние между двумя пристанями 60 км. Теплоход проходит это расстояние по течению и против течения за 5,5 часов. Найдите скорость теплохода в стоячей воде и скорость течения, если одна из них больше другой на 20 км/ч.
Краткая запись: пусть скорость теплохода х км/ч, а скорость течения реки у км/ч, тогда
| Скорость, км/ч | Путь, км | Время, ч | |
| По течению | х + у | 60 | 60/(х + у) |
| Против течения | х – у | 60 | 60/(х – у) |
Зная, что теплоход проходит это расстояние по течению и против течения реки за 5,5 часов и скорость катера больше скорости течения реки, составим систему двух уравнений с двумя неизвестными:
Ответ: 22 км/ч – скорость теплохода, 2 км/ч – скорость течения реки.
3. Решение задач (30 минут).
Фермер отправился на машине в город, находящийся на расстоянии 110 км от фермы. Через 20 минут из города на ферму выехал его сын, который проезжал в час на 5 км больше. Встреча произошла в 50 км от города. С какой скоростью ехал фермер?
Краткая запись: пусть скорость фермера х км/ч, а скорость сына у, тогда
| Скорость, км/ч | Путь, км | Время, ч | |
| Фермер | х | 110 – 50 = 60 | 60/х |
| Сын | у | 50 | 50/у |
Зная, что встреча произошла в 50 км от города, и сын выехал на 20 минут позже, составим систему уравнений с двумя неизвестными:
Второе решение не подходит по условию задачи.
Ответ: 45 км/ч скорость фермера.
Расстояние в 360 км легковой автомобиль прошел на 2 часа быстрее, чем грузовой. Если скорость каждого автомобиля увеличить на 30 км/ч, то грузовой затратит на весь путь на 1 час больше, чем легковой. Найдите скорость каждого автомобиля.
Краткая запись: пусть скорость легкового автомобиля х км/ч, а скорость грузового у км/ч, тогда:
| Скорость, км/ч | Путь, км | Время, ч | |
| Легковой | х | 360 | 360/х |
| Грузовой | у | 360 | 360/у |
| Скорость, км/ч | Путь, км | Время, ч | |
| Легковой | х + 30 | 360 | 360/(х + 30) |
| Грузовой | у + 30 | 360 | 360/(у + 30) |
Зная, что в первом случае легковой автомобиль приезжает на 2 часа раньше, а во втором на 1 час раньше, составим систему уравнений с двумя переменными:
Ответ: 90 км/ч скорость легкового автомобиля, 60 км/ч скорость грузового автомобиля.
Бассейн наполнится. Если первую трубу открыть на 12 минут, а вторую – на 7 минут. Если же обе трубы открыть на 6 минут. То наполнится 2/3 бассейна. За сколько минут наполнится бассейн, если открыть только вторую трубу?
Краткая запись: пусть весь объем воды в бассейне равен 1, производительность 1 трубы х , а второй – у, тогда:
| Производительность | Работа | Время, мин | |
| 1 труба | х | 12х | 12 |
| 2 труба | у | 7у |
| Производительность | Работа | Время, мин | |
| 1 труба | х | 6х | 6 |
| 2 труба | у | 6у | 6 |
Зная, что в первом случае бассейн наполнится полностью, а во втором только 2/3, составим систему двух уравнений с двумя неизвестными.
Ответ: за 15 минут вторая труба заполнит весь бассейн.
Двое рабочих могут выполнить задание за 12 дней. Если сначала один из них сделает половину всей работы, а потом остальное сделает другой, то им потребуется 25 дней. За сколько дней каждый рабочий, работая один, может выполнить задание?
Краткая запись: пусть производительность 1 рабочего х, а второго у, тогда:
| Производительность | Работа | Время | |
| 1 рабочий | х | 1/2 | 1/2х |
| 2 рабочий | у | 1/2 | 1/2у |
Зная, что вместе они сделают работу за 12 дней, а работая по очереди и выполнив по половине работы, им потребуется 25 дней, составим систему уравнений с двумя неизвестными:
Ответ: один рабочий выполнит всю работу за 30 дней, а другой за 20 дней.
4. Подведение итогов урока (2 минуты).
Домашнее задание: п. 22, №476, 479, 491.
- Учебник «Алгебра 9», автор Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е.
Видео:Математика | ЗАДАЧА 22 из ОГЭ. Задачи на работуСкачать
Решение задач на движение с помощью систем линейных уравнений
Презентация по решению задач на движение с помощью систем линейных уравнений. В презентации использованы фрагменты сборника визуализированных задач к учебнику 7 класса под ред. А.Г.Мерзляк, В.М.Поляков, разработанных Смирновой Ириной Сергеевной, учителем информатики лицея № 86 г.Ярославля.
Просмотр содержимого документа
«Решение задач на движение с помощью систем линейных уравнений»
Решение задач с помощью систем линейных уравнений.
Показать (2) 2 » width=»640″
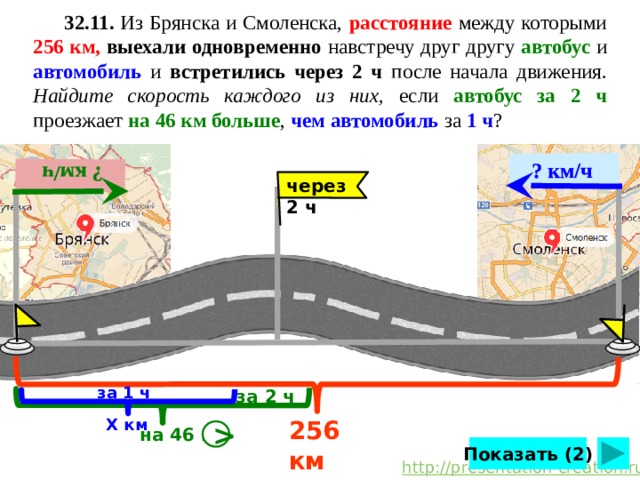
32.11. Из Брянска и Смоленска, расстояние между которыми 256 км, выехали одновременно навстречу друг другу автобус и автомобиль и встретились через 2 ч после начала движения. Найдите скорость каждого из них, если автобус за 2 ч проезжает на 46 км больше , чем автомобиль за 1 ч ?
А.Г.Мерзляк, В.М.Поляков 7 класс. №32.11 стр.225. Сделайте клик по кнопке «Показать» ( 2 раза)
Из Брянска и Смоленска, расстояние между которыми 256 км , выехали одновременно навстречу друг другу автобус и автомобиль и встретились через 2 ч после начала движения. Найдите скорость каждого из них, если автобус за 2 ч проезжает на 46 км больше , чем автомобиль за 1 ч ?
Первый этап . Составляем математическую модель задачи
Обозначим скорость автобуса – х км/ч, а скорость автомобиля — у км/ч. Автобус проезжает за 2 часа на 46 км больше, чем автомобиль за 1 час..
Составим и решим систему уравнений:
Из Брянска и Смоленска, расстояние между которыми 256 км , выехали одновременно навстречу друг другу автобус и автомобиль и встретились через 2 ч после начала движения. Найдите скорость каждого из них, если автобус за 2 ч проезжает на 46 км больше , чем автомобиль за 1 ч ?
Второй этап . Решаем систему линейных уравнений
Значит, скорость автобуса 58 км/ч, скорость автомобиля 70 км/ч.
Ответ: скорость автобуса 58 км/ч, скорость автомобиля 70 км/ч.
32.12. С двух станций, расстояние между которыми 300 км , одновременно навстречу друг другу отправились пассажирский и товарный поезда, которые встретились через 3 ч после начала движения. Если бы пассажирский поезд вышел на 1 ч раньше , чем товарный, то они встретились бы через 2,4 ч после выхода товарного поезда . Найдите скорость каждого поезда.
А.Г.Мерзляк, В.М.Поляков 7 класс. №32.12 стр.225. Сделайте клик по кнопке «Показать» (3 раза)
С двух станций, расстояние между которыми 300 км , одновременно навстречу друг другу отправились пассажирский и товарный поезда, которые встретились через 3 ч после начала движения. Если бы пассажирский поезд вышел на 1 ч раньше , чем товарный, то они встретились бы через 2,4 ч после выхода товарного поезда . Найдите скорость каждого поезда.
Составим и решим систему уравнений:
С двух станций, расстояние между которыми 300 км , одновременно навстречу друг другу отправились пассажирский и товарный поезда, которые встретились через 3 ч после начала движения. Если бы пассажирский поезд вышел на 1 ч раньше , чем товарный, то они встретились бы через 2,4 ч после выхода товарного поезда . Найдите скорость каждого поезда.
Значит, скорость пассажирского поезда 60 км/ч, скорость товарного – 40 км/ч.
Ответ: скорость пассажирского поезда 60 км/ч, скорость товарного – 40 км/ч.
8 » width=»640″
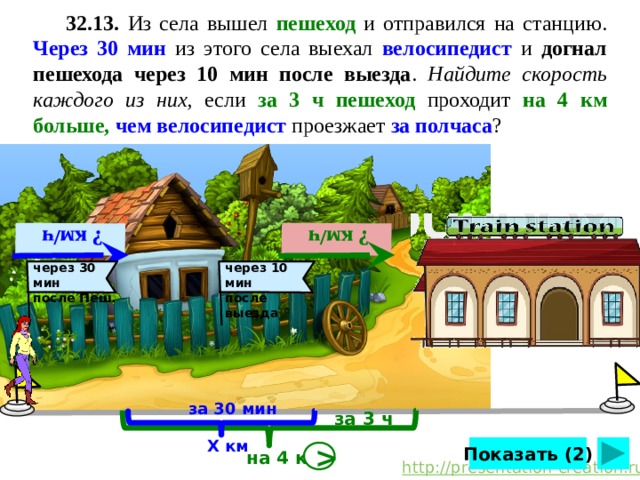
32.13. Из села вышел пешеход и отправился на станцию. Через 30 мин из этого села выехал велосипедист и догнал пешехода через 10 мин после выезда . Найдите скорость каждого из них, если за 3 ч пешеход проходит на 4 км больше, чем велосипедист проезжает за полчаса ?
А.Г.Мерзляк, В.М.Поляков 7 класс. №32.13 стр.226. Сделайте клик по кнопке «Показать» ( 2 раза)
Из села вышел пешеход и отправился на станцию. Через 30 мин из этого села выехал велосипедист и догнал пешехода через 10 мин после выезда . Найдите скорость каждого из них, если за 3 ч пешеход проходит на 4 км больше , чем велосипедист проезжает за полчаса ?
📽️ Видео
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЙ. §3 алгебра 7 классСкачать
Алгебра 8. Урок 12 - Задачи на составление дробно-рациональных уравнений (Часть 1)Скачать
Решение задач с помощью систем уравнений второй степени. Алгебра, 9 классСкачать
Эглит М.Э.- Основы механики сплошных сред - 12. Об определяющих соотношениях в моделях сплошных средСкачать
Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать
Решение задач с помощью уравнений.Скачать
Алгебра 8 класс (Урок№29 - Решение задач с помощью квадратных уравнений.)Скачать
Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать
Задачи на движение по воде | Математика | TutorOnlineСкачать
Решение задач с помощью рациональных уравнений. Алгебра, 8 классСкачать
Алгебра 7 класс (Урок№44 - Решение задач с помощью линейных уравнений.)Скачать
АЛГЕБРА 7 класс. Решение задач с помощью систем уравненийСкачать
Решение задач с помощью систем уравнений второй степени. Урок 17. Алгебра 9 классСкачать
9 класс. Алгебра. Решение задач с помощью систем уравнений.Скачать
Решение задач с помощью систем уравненийСкачать
