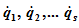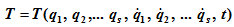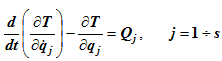Решение задач с решением на уравнение лагранжа 2 рода (5 видео)

Уравнения Лагранжа второго рода

При непосредственном использовании уравнений (24.4) для решения задач могут возникать трудности, связанные с вычислением обобщенных сил инерции Q’). Однако процесс составления уравнений значительно упростится, если выразить все входящие в них обобщенные силы через кинетическую энергию системы.

Лагранж получил формулу, выражающую обобщенную силу инерции, соответствующую какой-либо обобщенной координате q_i механической системы, в следующем виде:

Подставляя выражение (24.5) для Q» в равенства (24.4), получим следующую систему уравнений Лагранжа:

где T — кинетическая энергия механической системы; q_t — обобщенные координаты; Q, — обобщенные активные силы; s — число степеней свободы системы.

Равенства (24.6) и представляют собой дифференциальные уравнения движения механической системы в обобщенных координатах, или уравнения Лагранжа второго рода. Число уравнений Лагранжа второго рода равно числу степеней свободы системы.

Для составления уравнений Лагранжа надо кинетическую энергию механической системы выразить через обобщенные координаты и обобщенные скорости. При дифференцировании по времени первых членов в левых частях уравнений Лагранжа появятся вторые производные по времени от обобщенных координат (q).

Уравнения Лагранжа дают единый и притом достаточно простой метод решения задач динамики как для простых, так и для сложных механических систем. Важное преимущество этих уравнений состоит в том, что их вид и число не зависят ни от количества тел (или точек), входящих в систему, ни от того, как эти тела движутся. Если у механической системы связи идеальные, то в правые части уравнений (24.6) будут входить лишь обобщенные активные силы, что позволяет исключить из рассмотрения все реакции идеальных связей.

При применении уравнений Лагранжа второго рода для получения дифференциальных уравнений движения механической системы в обобщенных координатах рекомендуется такая последовательность действий:

1) исследовав подвижность системы, установить число ее степеней свободы и выбрать обобщенные координаты;
2) изобразить систему в произвольном положении (при положительных обобщенных координатах) и показать на рисунке все действующие на систему силы (для системы с идеальными связями только активные);
3) определить кинетическую энергию системы в ее произвольном движении (при одновременном изменении всех обобщенных координат) и выразить эту энергию через обобщенные координаты q_t и обобщенные скорости q_t;
4) выполнить предусмотренные уравнениями Лагранжа операции дифференцирования выражения кинетической энергии системы;

5) вычислить обобщенные силы Q_p последовательно задавая элементарные положительные приращения (5д, > 0) только соответствующей обобщенной координате;
6) подставить все полученные в п. 4 и 5 величины в уравнения Лагранжа второго рода (24.6).

Из полученных дифференциальных уравнений при заданных силах и начальных условиях можно, интегрируя эти уравнения, найти закон движения системы в виде уравнений (23.1). Если задан закон движения системы, то дифференциальные уравнения позволяют определить действующие на систему силы.

Задача 24.2. Механическая система (рис. 24.2) состоит из двухступенчатого шкива / (вес Р — 40 Н, радиусы ступеней R — 0,4 м, г — 0,2 м, радиус инерции относительно оси вращения р = 0,3 м), обмотанного нитями, на концах которых прикреплен груз 2 (вес Р₂ — 60 Н) и с помощью пружины каток 3 (вес Р₃ — 20 Н). Каток (сплошной однородный цилиндр) катится без скольжения по шероховатой наклонной плоскости с углом наклона а = 30°. Коэффициент жесткости пружины с= 150 Н/м. К шкиву приложена пара сил с моментом М — 80 Н • м , а к оси катка — сила F— 100 Н.

Составить для системы уравнения Лагранжа второго рода и определить: 1) x—j <t) —закон изменения удлинения пружины, считая, что движение началось из состояния покоя при недеформированной пружине (длину пружины в этом состоянии обозначим через /); 2) т — период колебаний, совершаемых телами системы при ее движении.

Решение. 1. Рассматриваемая система имеет две степени свободы. Выберем в качестве обобщенных координат угол ф поворота шкива и удлинение х пружины, т. е. q_x — ф, q₂ — х. Тогда уравнения Лагранжа второго рода будут иметь вид

2. На рис. 24.2 система изображена в произвольном положении (когда Ф > 0 и х > 0) и показаны все действующие на нее активные силы: сила F, силы тяжести Р_х, Р₂, /*₃, силы упругости пружины /у_Пр и 7 7 _у‘пр(/ 7 _упр — Fy_np — сх)

и пара сил с моментом М; реакции идеальных связей в точках О и К не изображаем.

3. Определим кинетическую энергию Т механической системы, равную сумме энергий всех ее тел:

Так как шкив вращается вокруг оси О, груз движется поступательно, а каток — плоскопараллельно, то

где моменты инерции тел вычисляются по формулам J₀=(P_]/g)p, J_B = (P₂/2g)R (R₃ — радиус катка 3).

Все входящие в равенства (в) скорости надо выразить через обобщенные скорости ф их. Очевидно, что со, =ф, V₂ = R(?>_<= Rg>. Для определения скорости V_B рассмотрим движение точки В как сложное, состоящее из переносного движения — движения точки D и относительного движения — движения точки В по отношению к точке D, происходящего за счет изменения расстояния BD вследствие деформации пружины. Следовательно,

Тогда, принимая во внимание, что при возрастании ф и х скорости V_B e и У_в направлены в противоположные стороны, получим V_B=rg>-x.

Учитывая, что точка К катка является его мгновенным центром скоростей, получим «3 = Vg/R₃ = (np-x)/R₃.

Подставив все найденные значения скоростей и значения J₀ и J_в в формулы (в), получим окончательно из равенства (б) следующее выражение для Т:

4. Выполняем операции дифференцирования выражения (г), предусмотренные в левой части уравнений Лагранжа второго рода (а):

Подставив в эти выражения числовые значения величин, получим

5. Теперь определим обобщенные силы, соответствующие каждой обобщенной координате.
1) Для определения (2_Ф сообщим системе возможное перемещение, при котором координата ф получает приращение 5ф > 0, а координата х не изменяется, т. е. 8.x =0. В этом случае груз 2 получает перемещение bs₂ = Rbcp, направленное вертикально вниз; так как пружина свою длину не изменяет, то точка D и центр В катка получают одинаковые перемещения 5s_D — bs_B — rbф, направленные вдоль наклонной плоскости вверх.

Элементарная работа действующих сил будет равна

Так как F_yn — F_ynp и в данном случае bs_B — bs_D, то выражение в скобках равно нулю. Заменив все величины их значениями, найдем

И наконец, определяем обобщенную силу Q :

Подставив числовые значения, получим Q_(p = 82 Н • м.

2) Для определения Q_x сообщим системе возможное перемещение, при котором координата х получает приращение Ьх > 0, а координата ф не изменяется, т. е. 8ф = 0. В этом случае шкив не поворачивается, точки А и D не перемещаются, а точка В получает перемещение 8х. Тогда элементарную работу совершают только силы F, Р₃ и 7^_Пр(/ 7 _уПр = сх):

Подставив числовые значения, получим Q_x = (110 — 150.x) Н.

6. Подставив все полученные в п. 4 и 5 величины в уравнения Лагранжа второго рода (а), получим следующие дифференциальные уравнения движения системы:

7. Для определения x—j <t)исключаем из уравнений (д) (р. С этой целью из первого уравнения системы уравнений (д) находим выражение величины ср = (82 +0,6lx)/ 1,47 и подставляем его во второе уравнение. После упрощений получим дифференциальное уравнение вида

где к 2 = 53,57 (к = 7,32), D = 51,26.

Общее решение уравнения (е) будет х = х, + х₂, где х, — общее решение однородного уравнения х+к 2 х = 0, которое имеет вид Xj = Cj cos kt + + C₂ sin kt, x₂ — частное решение уравнения (e). Исходя из вида правой части этого уравнения (D— const), будем искать решение х₂ в виде х₂ = = В= const. Подставив выражение х₂ в уравнение (е), получим В = = D/k 2 = 0,96.

Таким образом, общее решение уравнения (е) имеет вид:

где Cj и С₂ — постоянные интегрирования. Для их определения найдем еще производную х:

По начальным условиям при f = 0 х = 0, х =0 (движение начинается из состояния покоя, и пружина в этот момент не деформирована). Подставив эти величины в уравнения (ж) и (з), найдем С, = —D/k 2 = —0,96, С₂ = 0. Окончательно, подставив числовые значения величин, получим искомую зависимость х= J <t)в виде, м:

Отсюда видно, что центр В катка 3 совершает по отношению к точке D нити колебания, закон которых дает равенство (и); период колебаний т = 2л/к = 0,86 с -1 .

Ответ: х = 0,96[ 1 — cos(7,32/)l м, т = 0,86 с -1 .

Содержание

iSopromat.ru
Maple: составление уравнений Лагранжа 2 рода и метод избыточных координат
1. Метод избыточных координат
2. Maple-функции построения и анализа уравнений Лагранжа
3. Задача о маятнике на тонкой нерастяжимой нити
Вместо заключения
🔥 Видео

Видео:Уравнения Лагранжа второго родаСкачать

iSopromat.ru

Уравнения Лагранжа второго рода, которые представляют собой дифференциальные уравнения второго порядка относительно обобщенных координат.

Для такой системы можно записать s уравнений, которые называются уравнениями Лагранжа второго рода или дифференциальными уравнениями движения в обобщенных координатах:

Уравнения Лагранжа второго рода могут быть обобщены на случай связей, осуществляемых с трением, хотя они и не являются идеальными. Для этого следует силу трения перенести из группы сил реакции в группу активных сил, тогда связь с трением можно формально считать идеальной.

Уравнения Лагранжа второго рода представляют собой дифференциальные уравнения второго порядка относительно обобщенных координат q₁, q₂,…q_s.

Дважды интегрируя эти уравнения и определяя по начальным условиям постоянные интегрирования, получим систему уравнений движения в обобщенных координатах:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Уравнения Лагранжа второго рода. Задача 1Скачать

Maple: составление уравнений Лагранжа 2 рода и метод избыточных координат

По роду профессиональной и научной деятельности я механик. Преподаю теоретическую механику в университете, пишу докторскую диссертацию в области динамики подвижного состава железных дорог. В общем, эта наука поглощает большую часть моего рабочего и даже свободного времени.

С Maple (на кафедре была 6-я версия, а у лоточников домой была куплена 8-я) познакомился ещё студентом, когда начинал работать над будущей кандидатской под крылом моего первого (ныше покойного) научного руководителя. Были и добрые люди, что помогли на самом первом этапе разобраться с пакетом и начать работать.

И вот так постепенно на его плечи была переложена большая часть вычислительной работы по подготовке диссертации. Диссертация была защищена, а Maple навсегда остался надёжным помошником в научном труде. Часто бывает необходимо быстро оценить какую-нибудь задачу, составить уравнения, исследовать их аналитически, быстро получить численное решение, построить графики. В этом отношении Maple просто незаменим для меня (ни в коем разе не хочу обидеть приверженцев других пакетов).

Сделать всё то, что будет предложено читателю под катом, меня подвигла задача принесенная ученицей (приходится ещё заниматься и репетиторством) со школьной олимпиады. Условие задачи таково:

Груз, висящий на нити длины L = 1,1 м, привязанной к гвоздю, толкнули так, что он поднялся, а затем ударился в гвоздь. Какова его скорость в момент удара о гвоздь? Ускорение свободного падения g = 10 м/с 2 .

Если не придираться к некоторонной туманности условия, то задача достаточно проста, а её решение, полученное путем довольно громоздких для школьника выкладок, в общем виде дает результат

И вот тут захотелось проверить решение, полученное с оглядкой на школьную программу по физике независимым способом, например составив дифференциальные уравнения движения этого маятника, да не просто, а с учетом освобождения от связи (в процессе движения нить, считаемая невесомой, провисает и маятник движется как свободная точка).

Это послужило катализатором для того, чтобы взять да и откопать свои старые задумки, накопленные ещё со времен работы в оргкомитете Всероссийской Олимпиады студентов по теоретической механике — три года подряд занимался там подготовкой задач компьютерного конкурса. Задумки касались автоматизации построения уравнений движений для механических систем с неудерживающими связями и трением, используя известные всем уравнения Лагранжа 2 рода

поборов стереотип многих преподавателей о том, что уравнения эти неприменимы к системам с неудерживающими связями и трением.

Что касается Maple, то его библиотека для решения задач вариационного исчисления дает возможность быстро получить уравнения Эйлера-Лагранжа, решение которых минимизирует действие по Гамильтону, что применимо для консервативных систем

где — функция Лагранжа, равная разности кинетической и потенциальной энергий системы.

Так как расматриваемые задачи не относятся к классу консервативных, то автором была предпринята попытка самостоятельно реализовать автоматизацию построения и анализа уравнений движений. Что из этого вышло, изложено под катом

Видео:Система с двумя степенями свободыСкачать

1. Метод избыточных координат

Рассматриваем механическую систему, имеющую s степеней свободы, положение которой описывается вектором обобщенных координат . Пусть также имеется r неудерживающих связей, к числу реакций которых можно причислить и трение покоя, при превышении предельного значения переходящее в активную силу трения скольжения, направление которой противоположно направлению относительной скорости скольжения.

Учет неудерживающих связей требует от нас определения и анализа величины их реакций, поэтому необходимо так же определить их величину. Уберем указанные связи и введем дополнительно r обобщенных координат, выразив через них кинетическую энергию системы

Составим s + r уравнений движения в форме уравнений Лагранжа 2 рода

содержащие s+r неизвестных координат и r неизвестных реакций связей. Считая связи удерживающими, дополняем данную систему уравнениями связей (для простоты рассматривая геометрические связи) в виде

получаем замкнутую систему уравнений, из которой находятся значения реакций

являющиеся функциями первых s (независимых) обобщенных координат и скоростей и они могут быть расчитаны на любом шаге интегрирования уравнений движения (1). Для удерживающих связей типа «нить/поверхность» уравнения (1) и (2) надо дополнить условием освобождения от связи

а для связей с сухим трением вида

где F_j и N_j соответственно касательная и нормальная составляющая реакции; v_j — проекция скорости относительного проскальзывани точки приложения реакции.

Таким образом, уравнения (1) — (4) представляют собой полную математическую модель движения рассматриваемой механической системы.

Засим с теорией можно покончить и перейти к практике

Видео:Уравнение Лагранжа 2-го рода. Линейная координатаСкачать

2. Maple-функции построения и анализа уравнений Лагранжа

Для решения этой задачи была написана Maple-библиотека lagrange, содержащая четыре функции

LagrangeEQs — построение уравнений движения в форме Лагранжа 2 рода

В качестве входных параметров функция принимает выражение кинетической энергии T как функцию обобщенных координат и обобщенных скоростей; массив обобщенных координат q; массив радиус-векторов точек приложения сил r и массив векторов сил F.

LinksEQs — получение уравнений дифференциальных связей из уравнений геометрических связей

Здесь надо отметить, что система уравнений геометрических связей eqs должна содержать избыточные координаты в явном виде, то есть иметь вид

в противном случае функции библиотеки не смогут обработать уравнения правильно. Для тестирования возможностей библиотеки сойдет и так, но в дальнейшем этот момент будет переработан: просто пока неясно, будет ли гарантированно разрешена система уравнений связи относительно угловых избыточных координат.

ReduceSystem — преобразование уравнений движения с учетом уравнений связей

Данный код в подробных пояснениях не нуждается — тут выполняется подстановка избыточных обобщенных координат, скоростей и ускорений, выражаемых уравнениями геометрических и дифференциальных связей в уравнения движения, с целью приведения их к виду, пригодному для вычисления реакций неудерживающих связей

SolveAccelsReacts — решение уравнений движения относительно реакций и обобщенных ускорений

Данная функция принимает на вход систему уравнений движения eqs, преобразованную с учетом уравнений связей. Она линейна относительно вторых производных независимых координат и реакций связей. Другие входные параметры: q — вектор независимых координат; R — массив реакций, относительно которых необходимо разрешить уравнения движения.

Теперь проиллюстрируем, как применять описанное «хозяйство» в деле

Видео:Задача на составление уравнения Лагранжа 2-го родаСкачать

3. Задача о маятнике на тонкой нерастяжимой нити

Расчетная схема будет такой. В качестве обобщенной координаты выбираем угол наклона нити к вертикали.

Поскольку нить — неудерживающая связь, нас будет интересовать её реакция, а значит введем дополнительную, избыточную координату r(t).

Приступаем. Чистим память и подключаем библиотеку линейной алгебры

Подключаем библиотеку lagrange

Определяем вектор обобщенных координат, вычисляем координаты и скорость груза, а так же кинетическую энергию системы

На выходе получаем выражение для кинетической энергии (для вставки сюда использована функция latex(), генерирующая результат в LaTeX-нотации)

Формируем массив сил и массив координат точек их приложения

Скармливаем всё функции LagrangeEQs()

получая на выходе уравнения движения

Нетрудно убедится, что функция отработала нормально — для иллюстрации специально выбрана не слишком громоздкая задача.

Далее задаем уравнение связи — пока нить натянута, справедливо условие

преобразуем систему с учетом этого условия и находим реакцию связи

Сила натяжения нити равна

Система (5) — (7) является полной системой уравнений движения груза, с учетом возможности провисания нити. Теперь подготовим её к численному интегрированию. Для начала разрешим её относительно ускорений, передав в SolveAccelsReacts() уравнения (5) и (6), вектор обобщенных координат и пустой массив реакций

получая на выходе

Для численного моделирования, хоть это и не спортивно, напишем отдельный код, дабы не забивать голову читателя длительной обработкой полученной системы напильником. Тем более что моделирование будет иметь свои особенности.

Готовим исходные данные и систему уравнений движения

Строим функцию вычисления состояния системы, при заданной горизонтальной начальной скорости груза

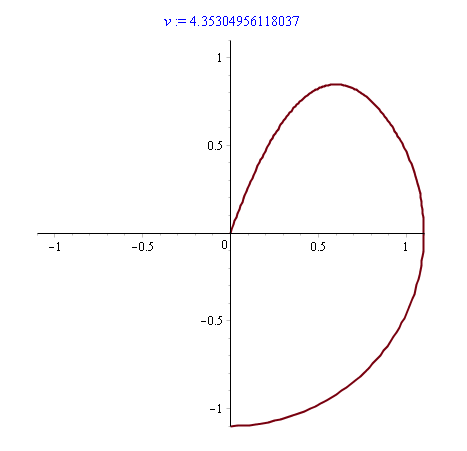
Теперь проверяем «школьное» решение задачи

В итоге, получаем результат, приведенный на скриншоте. Скорость груза в момент удара соответствует приведенному в предисловии значению, и видно, что до провисания нити груз движется по окружности, а после провисания нити движется как свободная точка под действием силы тяжести, по параболе.

Замечу, что погрешности попадания в гвоздь — вынужденная мера: в полярных координатах, которые были использованы, задача имеет особенность, понятную из уравнения (8). Поэтому r(t) сравнивалось не с нулем, а с величиной eps достаточно малой, чтобы получить решение, и достаточно большой, чтобы численный решатель fsolve() не сходил с ума. Однако это нисколько не умаляет практической ценности изложенных результатов.

Видео:Т. Уравнения Лагранжа 2 рода. Теория.Скачать

Вместо заключения

Возможно, читатель упрекнет меня, что я стреляю из пушки по воробьям. Однако, хочется заметить, что всё сложное начинается с простого, а большая наука — с малых задач.

Тестовую версию библиотеки можно качнуть тут