Решение задач с помощью систем уравнений 8 класс никольский

Разделы: Математика

Особое место в школьном курсе математики занимают текстовые задачи. Следует отметить, что, решая на уроках алгебры текстовые задачи, учитель математики работает не только на себя, подготавливая учеников к умению осмыслить текст задач в курсе геометрии, без чего говорить о возможности решения этих задач бессмысленно, но также помогает преподавателям физики, химии и даже литературы, так как для того чтобы решить задачу необходимо внимательно прочитать текст задачи, понять его, выделить главное, т.е. разложить все данные «по полочкам».
Не случайно, оценивая задачу, решаемую с помощью уравнения или системы уравнений, учитель отдельно оценивает верность составленного уравнения или системы, так как добросовестного ученика безусловно можно обучить различным математическим алгоритмам, но умению думать научить без текстовых задач невозможно.

Урок рассчитан на один час.

Цель урока: выработка умений самостоятельного применения знаний в стандартных и нестандартных ситуациях.

Задача № 386а (по учебнику «Алгебра-8», С.М.Никольский и др., 2006 г.)

Расстояние между двумя населенными пунктами 50 км. Из этих пунктов одновременно навстречу друг другу выехали мотоциклист и велосипедист. Скорость мотоциклиста на 30 км/час больше. Встретились они на расстоянии 10 км от одного из населенных пунктов. Какова скорость велосипедиста?

1. Определить, кто удалится на большее расстояние от начальной точки своего движения.
2. Определить, какую величину удобнее принять за х.
3. Составить таблицу, систематизирующую данные задачи и подводящую к составлению уравнения.

V, км/ч

Мотоциклист

х + 30

40/(х + 30)

50 – 10 = 40

Велосипедист

Составим уравнение: .

Это уравнение имеет единственный корень х = 10. Итак, скорость велосипедиста 10 км/ч.

Задача № 395 (по учебнику «Алгебра-8», С.М.Никольский и др., 2006 г.)

Двое рабочих выполнили некоторую работу за 8 ч. Первый из них, работая отдельно, может выполнить ту же работу на 12ч быстрее второго, если тот будет работать отдельно. За сколько часов второй рабочий один может выполнить ту же работу?

1. Отметить, что задачи на совместную работу знакомы ученикам с 5-го класса.
2. Обратить внимание на то, что «быстрее» значит меньше времени.
3. Определить, какую величину удобнее принять за х.
4. Составить таблицу, систематизирующую данные задачи и подводящую к составлению уравнения.

Производительность (работа/ч)

Работа (работа)

1-ый рабочий

х – 12

1/(х – 12)

2-ой рабочий

1-ый и 2-ой вместе

Составим уравнение: .

Это уравнение имеет два положительных корня х = 4 и х = 24. Так как при х = 4 время работы 1-го рабочего будет равно 4 – 12

V, км/ч

Автобус

(80 – х)/50

40 + (40 – х) = 80 – х

Велосипедист

Составим уравнение: .

Это уравнение имеет единственный корень . Итак, велосипедист и автобус встретятся на расстоянии км от первого населенного пункта.

Задача № 260(1) (из экзаменационного сборника по алгебре за курс основной школы, 9 класс, Л.В.Кузнецова и др.).

На соревнованиях по кольцевой трассе один лыжник проходил круг на 2мин быстрее другого и через час обогнал его ровно на круг. За сколько минут каждый лыжник проходит круг?

1. Обратить внимание на то, что вместо привычной величины «скорость» в этой задаче на движение необходимо найти период вращения, измеряемый в мин/круг. Для этого уместно предложить ученикам устную задачу: Лыжник проходит два круга за 10мин. За сколько минут лыжник пройдет один круг? Что является делимым, а что делителем в ходе решения этой задачи?
2. Обратить внимание, что [мин] : [мин/круг] = [круг].
3. Привести все данные в единую систему измерений: 1 ч = 60 мин.
4. Определить, какую величину удобнее принять за х.
5. Составить таблицу, систематизирующую данные задачи и подводящую к составлению уравнения.

T, мин/круг

t, мин

S, круги

1-ый лыжник

2-ой лыжник

60/(х + 2)

1) Составим уравнение: .

Это уравнение имеет два корня: х = – 12 и х = 10. Так как по смыслу задачи х > 0, то х = 10.

2) 10 + 2 = 12 (мин). Итак, первый лыжник проходит круг за 10 мин, а второй за 12 мин.

Итоги урока:

1. Повторили табличный способ систематизации данных задачи, при необходимости дополненный рисунком.
2. Еще раз обратили внимание на то, что задача решается в единой системе измерений.
3. Отметили, что если уравнение, составленное к задаче, имеет два корня, то полученные решения требуют смысловой проверки.
4. Обратили внимание на то, что нельзя решать задачу «автоматически»; необходимо прежде всего внимательно ее прочитать, оценить в каких единицах измеряется каждая величина, данная в задаче, как эти величины связаны между собой и той величиной, которую следует найти, и только после этого, выбрав способ решения, приступить к самому решению.

Домашнее задание: Задачи №№393, 391в (Алгебра-8, С.М. Никольский и др., 2006 г.).

Комментарий: представляется целесообразным на первом уроке по данной теме рассмотреть задачи одного плана (здесь – на движение и работу), приводящие к достаточно простым уравнениям.

Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

Урок по теме «Решение задач с помощью систем уравнений»

Урок по учебнику «Алгебра 8 класс» под редакцией Г. В. Дорофеева. Цель урока: учить учащихся решать текстовые задачи с помощью систем уравнений как математических моделей реальных ситуаций. На уроке применяется технология проблемного обучения.

Просмотр содержимого документа
«Урок по теме «Решение задач с помощью систем уравнений»»

«Я могу ошибаться,

и ты можешь ошибаться,

но совместными усилиями

мы можем постепенно

приближаться к истине»

Маме и дочке вместе 28 лет. Мама старше дочери на 22 года. Сколько лет дочке?

Маме и дочке вместе 28 лет. Мама старше дочери на 22 года. Сколько лет дочке?

• Способ решения: дочке Х лет, маме Х+22, вместе им 28, то есть Х+Х+22=28 = 2Х=28-22 = 2Х=6 = Х=6/2 = Х=3, таким образом нашли возраст дочери, 3 года. Маме же 3+22=25 лет.
• Получаем ответ: матери 25 лет, дочери 3 года.

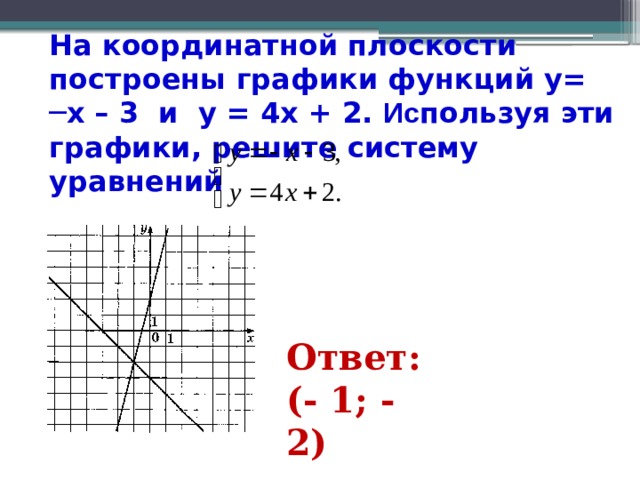
На координатной плоскости построены графики функций y= ─x – 3 и y = 4x + 2. Ис пользуя эти графики, решите систему уравнений

Каким способом можно решить систему уравнений ?

Методы решения систем линейных уравнений с двумя переменными

• Метод алгебраического сложения
• Графическийметод
• Метод подстановки

Проблема! Как решить задачу?

Прямоугольный участок площадью 2400 м 2 нужно оградить забором длиной 200 м. Найти длину и ширину участка.

Прямоугольный участок площадью 2400 м 2 нужно оградить забором длиной 200 м. Найти длину и ширину участка.

Прямоугольный участок площадью 2400 м 2 нужно оградить забором длиной 200 м. Найти длину и ширину участка.

Ответ: 40м и 60м

По учебнику стр. 205-207

Алгоритм решения задачи

• Анализ условия.
• Введение неизвестных
• Выделение двух ситуаций
• Установление зависимости между данными задачи и неизвестным
• Составление уравнений
• Решение системы уравнений
• Запись ответа.

учебник стр. 208

• № 665 (а)
• № 666 (а)

Подведём итог урока

Рефлексия Выберите вариант соответствующий вашему ощущению после сегодняшнего урока. 1. Я все знаю, понял и могу объяснить другим! 2. Я все знаю, понял, но не уверен, что смогу объяснить другому. 3. Я сам знаю, понял, но объяснить другому не смогу. 4. У меня остались некоторые вопросы.

Видео:Урок по теме РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ 7 КЛАСССкачать

ГДЗ: Алгебра 8 класс Потапов, Шевкин — Дидактические материалы

Дидактические материалы по алгебре для 8 класса под редакцией Потапова — это сборник заданий для самостоятельных, контрольных и итоговых работ. В качестве дополнения здесь даются задачи повышенной сложности, которые можно использовать при подготовке к школьным и городским олимпиадам. Задания усложняются постепенно и делятся на 2 уровня – базовый и высокий. В результате у учителя есть возможность корректно оценить каждого ученика.

Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

Структура тетради с дидактическими материалами

1 итоговую работу.

Все задания даны в 4 вариантах. Подходит к учебнику «МГУ – в школе». Пособие используется для организации работы на уроке, номера могут задаваться в качестве домашних упражнений.

Видео:АЛГЕБРА 7 класс. Решение задач с помощью систем уравненийСкачать

Преимущества дидактических материалов

Первая часть заданий нацелена на каждого ученика. Автор предлагает выполнить номера по образцу, что существенно облегчает решение. Здесь содержатся подробные объяснения, которые позволяют подготовиться к предстоящему уроку самостоятельно. В пособие включены задания со звездочкой. Они рекомендованы к использованию в классах с углубленным изучением математики. Номера в каждой работе даны в избытке. Автор предлагает учителям выбрать подходящие упражнения на свое усмотрение. Первый и второй варианты рассчитаны на учащихся общеобразовательных школ. Третьи и четвертые направлены на школьников математических гимназий и лицеев.

Видео:Решение задач с помощью систем уравненийСкачать

Как все выполнить самостоятельно

Хотите подготовиться к уроку и решить все задания на «отлично»? Вам поможет решебник к учебнику «Алгебра 8 класс Дидактические материалы Потапов, Шевкин Просвещение». Онлайн-пособие содержит решение и ответы на все номера. Изображения доступны в режиме онлайн. ГДЗ (готовые домашние задания) рекомендовано использовать для проверки знаний и правильности решения упражнений.

📽️ Видео

Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

8 класс. Алгебра. Задачи на движениеСкачать

Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

Типичная ОГЭшная задача для тех, кто не знает тригонометриюСкачать

Решение задач с помощью систем уравненийСкачать

Как проверяют учеников перед ЕНТСкачать

Решение систем уравнений второго порядка. 8 класс.Скачать

Алгебра 8 класс (Урок№32 - Решение задач с помощью рациональных уравнений.)Скачать

Решение задач с помощью систем уравнений, 7 классСкачать

Решение задач с помощью систем уравнений | Алгебра 7 класс #48 | ИнфоурокСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Алгебра 8 класс (Урок№29 - Решение задач с помощью квадратных уравнений.)Скачать

8 04 7 класс решение задач с помощью систем уравненийСкачать

Алгебра 8. Урок 12 - Задачи на составление дробно-рациональных уравнений (Часть 1)Скачать

Решение задач с помощью систем уравнений второй степени. Алгебра, 9 классСкачать