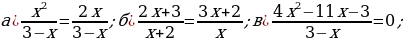Решение задач с помощью рациональных уравнений 8 класс самостоятельная работа с ответами

Видео:Решение задач с помощью рациональных уравнений. Алгебра, 8 классСкачать

ГДЗ дидактические материалы по алгебре 8 класс Потапов, Никольский, Шевкин Задание: Вариант 1

1. Товарный поезд должен пройти с постоянной скоростью расстояние между станциями, равное 420 км. Когда он прошел половину этого расстояния, то был задержан у светофора на 30 мин, поэтому, чтобы наверстать опоздание, машинист увеличил скорость поезда на 10 км/ч. С какой скоростью поезд шел до остановки?

2. Два велосипедиста выехали одновременно навстречу друг другу из двух сел A и B. Первый прибыл в B через 16 минут после встречи, а второй прибыл в A через 25 минут после встречи. Через сколько минут после выезда из своих сёл они встретились?

3. Пассажир преодолел 170 км. При этом на автобусе он ехал 1 час, а на поезде 2 часа. Найдите скорость автобуса, если каждые 10 км он преодолевал на 2 мин медленнее, чем поезд.

Видео:Алгебра 8 класс (Урок№32 - Решение задач с помощью рациональных уравнений.)Скачать

Самостоятельная работа . Решение дробных рациональных уравнений. Решение задач с помощью рациональных уравнений.

Просмотр содержимого документа
«Самостоятельная работа . Решение дробных рациональных уравнений. Решение задач с помощью рациональных уравнений.»

Самостоятельная работа 8 класс

Решение дробных рациональных уравнений.

Решение задач с помощью рациональных уравнений

№ 1 Решите уравнение: .

№2 Теплоход, собственная скорость которого 18км/ч прошёл 50 км по течению реки и 8 км против течения, затратив на весь путь 3ч.Какова скорость течения реки?

№3 Два куска латуни имеют массу 30 кг. Первый кусок содержит 5 кг чистой меди, а второй кусок – 4 кг. Сколько процентов меди содержит первый кусок латуни, если второй содержит на 15% больше первого?

№ 1 Решите уравнение:

.

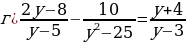
№2 Катер прошёл 40 км по течению реки и 6км против течения, затратив на весь путь 3ч. Какова собственная скорость катера, если скорость течения реки 2 км/ч?

№3 Одна бригада выполняла задание в течение 3,5 дня. Сменившая ее бригада закончила работу за 6 дней. Сколько дней выполняла бы задание каждая из бригад, если известно, что вторая бригада выполняла бы задание на 5 дней больше первой?

Видео:Решение задач с помощью рациональных уравнений. Видеоурок 20. Алгебра 8 классСкачать

Самостоятельная работа по теме: «Решение задач составлением дробного рационального уравнения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

1. Лодка за одно и то же время может проплыть 36 км по течению реки или 20 км – против течения. Найдите скорость лодки по течению реки, если скорость течения составляет 2 км/ч.

2. Велосипедист проехал 24 км, а мотоциклист – 10 км. Скорость мотоциклиста на 18 км/ч больше скорости велосипедиста. Найдите скорости обоих, если известно, что велосипедист был в пути на 1 час больше, чем мотоциклист.

3. Грузчики планировали за некоторое время разгрузить 160 ящиков. Однако они справились с работой на три часа раньше срока, так как разгружали в час на 12 ящиков больше, чем планировали раньше. Сколько ящиков в час они разгружали на самом деле?

1. Моторная лодка за одно и то же время может проплыть 36 км против течения реки или 48 км – по течению. Найдите скорость лодки против течения реки, если скорость течения составляет 2 км/ч.

2. Пешеход прошел 15 км, а велосипедист проехал 27 км. Скорость велосипедиста на 12 км/ч больше скорости пешехода. Найдите скорости обоих, если известно, что велосипедист был в пути на 1 час меньше, чем пешеход.

3. Машинистка должна была напечатать за определенное время 200 страниц. Печатая в день на 5 страниц больше, чем планировала, она завершила работу на два дня раньше срока. Сколько страниц в день печатала на самом деле машинистка?

1. За одно и то же время велосипедист проехал 4 км, а мотоциклист – 10 км. Скорость мотоциклиста на 18 км/ч больше скорости велосипедиста. Найдите скорость мотоциклиста.

2. Скорость течения реки на 5 км/ч меньше собственной скорости моторной лодки. Найдите обе эти скорости, если 18 км по течению лодка проплывает на 1 час быстрее, чем 15 км против течения реки.

3. Два трактора израсходовали 168 литров горючего, причем первый израсходовал в час на 1 литр меньше, чем второй, а работал на два часа больше. Сколько горючего в час расходовал каждый трактор, если они израсходовали горючего поровну?

1. За одно и то же время пешеход прошел 5 км, а велосипедист проехал 15 км. Скорость велосипедиста на 12 км/ч больше скорости пешехода. С какой скоростью двигался велосипедист?

2. Собственная скорость моторной лодки на 12 км/ч больше скорости течения реки. Найдите обе эти скорости, если 36 км против течению лодка проплывает на 1 час медленнее, чем 32 км по течению реки.

3. Два ателье сшили 252 костюма. Первое ателье изготавливало в день на два костюма больше, чем второе, и затратило на всю работу на четыре дня меньше. Сколько костюмов в день изготавливало в день каждое ателье, если они сшили одинаковое количество костюмов?

1. Весельная лодка за одно и то же время может проплыть 18 км по морю или 10 км – против течения реки. Найдите скорость лодки по течению реки, если скорость течения составляет 2 км/ч.

2. Велосипедист проехал 30 км, а пешеход прошел 25 км. Скорость пешехода на 10 км/ч меньше скорости велосипедиста. Найдите скорости обоих, если известно, что пешеход был в пути на 3 часа дольше, чем велосипедист.

3. Грузчики планировали за некоторое время разгрузить 200 ящиков. Однако они справились с работой на час раньше срока, так как разгружали в час на 10 ящиков больше, чем планировали раньше. Сколько ящиков в час они разгружали на самом деле?

1. Моторная лодка за одно и то же время может проплыть 18 км по морю или 20 км – по течению реки. Найдите скорость лодки против течения реки, если скорость течения составляет 2 км/ч.

2. Спортсмен-бегун пробежал дистанцию в 16 км на час быстрее, чем велосипедист проехал 24 км. Найдите скорости обоих, если известно, что скорость бегуна на 16 км/ч меньше скорости велосипедиста.

3. Машинистка должна была напечатать за определенное время 160 страниц. Печатая в день на 4 страницы больше, чем планировала, она завершила работу на два дня раньше срока. Сколько страниц в день печатала на самом деле машинистка?

1. За одно и то же время пешеход прошел 6 км, а велосипедист проехал 18 км. Скорость пешехода на 10 км/ч меньше скорости велосипедиста. Найдите скорость велосипедиста.

2. Скорость течения реки на 2,5 км/ч меньше собственной скорости весельной лодки. Найдите обе эти скорости, если 27 км по морю лодка проплывает на 2 часа медленнее, чем 26 км по течению реки.

3. Два трактора израсходовали 144 литра горючего, причем первый израсходовал в час на 1 литр меньше, чем второй, а работал на час больше. Сколько горючего в час расходовал каждый трактор, если они израсходовали горючего поровну?

1. За одно и то же время бегун пробежал 1 км, а велосипедист проехал 3 км. Скорость бегуна на 16 км/ч меньше скорости велосипедиста. С какой скоростью двигался велосипедист?

2. Скорость моторной лодки на 16 км/ч больше скорости течения реки. Найдите обе эти скорости, если 27 км по морю лодка проплывает на час быстрее, чем 40 км против течения реки.

3. Два ателье сшили 180 костюмов. Первое ателье изготавливало в день на один костюм больше, чем второе, и затратило на всю работу на три дня меньше. Сколько костюмов в день изготавливало в день каждое ателье, если они сшили одинаковое количество костюмов?

СР по решению задач составлением дробного рационального уравнения

📸 Видео

Решение дробных рациональных уравнений. Алгебра, 8 классСкачать

Дробно-рациональные уравнения. 8 класс.Скачать

решение задач с помощью рациональных уравнений 8 класс алгебра № 619Скачать

Алгебра 8. Урок 12 - Задачи на составление дробно-рациональных уравнений (Часть 1)Скачать

8 класс, 28 урок, Рациональные уравнения как математические модели реальных ситуацийСкачать

Алгебра 8. Урок 14 - Задачи на составление дробно-рациональных уравнений (Часть 3)Скачать

Решение задач с помощью рациональных уравненийСкачать

Решение задач с помощью рациональных уравнений (урок 1))Скачать

8 класс Решение задач с помощью рациональных уравнений.Скачать

Алгебра 8 класс (Урок№29 - Решение задач с помощью квадратных уравнений.)Скачать

Алгебра 8 класс 23 неделя Решение задач с помощью рациональных уравненийСкачать

Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Подготовка к ЕГЭ по ХимииСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Рациональные уравнения как модели реальных ситуаций. §24 алгебра 8 классСкачать

Алгебра 8. Урок 13 - Задачи на составление дробно-рациональных уравнений (Часть 2)Скачать

Дробно-рациональные уравнения. Подготовка к экзаменам. 60 часть. 9 класс.Скачать

Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать