план-конспект урока по алгебре (8 класс) по теме
Урок изучения нового материала.
Предметы точных дисциплин(раздел – алгебра ,8 класс)
Богомолова Татьяна Ефимовна
МБОУ «Верхнекармальская ООШ» Черемшанского муниципального района
Тема : Определение квадратного уравнения. Неполные квадратные уравнения.
Цель: ввести определение квадратного уравнения, неполных квадратных уравнений и их решения; учить решать неполные квадратные уравнения; развивать логическое мышление учащихся, внимательность , аккуратность оформления решения неполных квадратных уравнений.
Оборудование: мультимедийная доска, ноутбук, портрет К.Гаусса, карточки –задания ,карточки- ответы.
Учитель : «Здравствуйте ,ребята, садитесь»
2.Устная работа.(написаны задания на доске)
Вспомним квадратные корни из некоторых чисел ,из их ответов попробуем получить русскую пословицу.
1)√225 +3√121= карточка со словом –кто (с другой стороны число) 48
2)√16 + √100 = карточка со словом –хочет (с другой стороны) 14
3) √25 * √225 = карточка со словом- много(с другой стороны) 75
4) — 0,3√10000 = карточкасо словом –знать ( с другой стороны) -30
5) √36/√121= карточка со словом –тому (с другой стороны) 6/11
6) √25= карточка со словом – мало (с другой стороны) 5
7) √81*25 = карточка со словом – надо (с другой стороны) 45
8) -√64= карточка со словом –спать(с другой стороны) 8
Мы с вами вспомнили свойства арифметического квадратного корня.
Теперь разложим на множители:
а) х²- 7х= (дети пишут ответ) х (х-7)
г) 4х² + 2х = 2х(2х +1)
х² -25= карточка со словом –математика (с другой другой стороны Ответ) х=- 5 и х= 5
х² = 5 карточка со словом- царица (с другой стороны)х= √5, х=-√5
х² + 9=0 карточка со словом – наук (с другой стороны) корней нет.
Мы с вами получили высказывание ученого математики Чьё это высказывание? (показывает портрет Гаусса. Немного биографии: Карл Гаусс(1777-1855) немецкий математик, астроном, геодезист, физик .Родился 30 апреля в Германии. Он был «принцем математиков». Единственный сын бедных родителей, очень талантливый ученик в школе.)
Почему он назвал математику «царицей наук»?
-(ответ учащихся) Без математики никуда, на уроках математики решаются системы упражнений, направленных на развитие мышления, памяти ,искать красивые решения.
Учитель : « Открыли тетради, запишите тему урока»
Тема на мультимедийной доске
Определение квадратного уравнения .Неполные квадратные уравнения.
Учитель: какой вид имеет линейное уравнение.
Учащийся: ах +в = 0
Учитель : А какой вид имеет квадратное уравнение?
Давайте посмотрим на таблицу.
Квадратное уравнение
ах² + вх+с =0
а- первый(старший )коэффициент
в- второй коэффициент
с – свободный член
а ≠ 0
Например :найдите из этих уравнений квадратные
(уравнения на мультимедийной доске)
1)3,6х² +4х – 6 =0 5) — 6х +12 =0
2) х+х²- 4 =0 6) 6х²+3х=0
3)15х²- х³-5 =0 7) — 0,5х²+ 2х – 8=0
4) 3х²- 18=0 8) х²+15х – 3 =0
Учащиеся отвечают :под номером 1,2,4,6.7,8.
Учитель: Правильно. А теперь посмотрим на следующую таблицу на доске
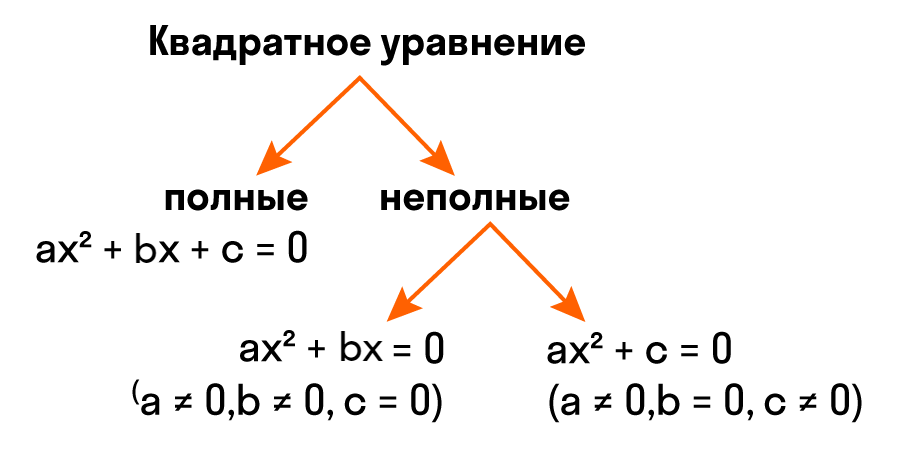
Виды квадратных уравнений.
х²+ вх+с=0, а=1 – приведенное квадратное уравнение
ах² +вх=0
ах² + с = о — неполные квадратные уравнения , а≠0
Посмотрите внимательно на уравнения, чем они отличаются от основного квадратного уравнения ах²+вх+с=0
Ученики: в первом уравнении а=1,во втором уравнении нет с,в третьем уравнении нет в .
Учитель: Даны квадратные уравнения, изучите их структуру, в чем их различие между собой.
(Уравнения на ноутбуке ,на мультимедийной доске:
1)х² + 4х+5 = 0 3) х²- 5х +6 = 0 5) х²- 9=0
2)х²- 15х- 3 =0 4) х²- 6х =0 6) х²+5 =0
Ученики:1,2.3- приведенные,4,5,6 –неполные.
Ученики:1,2,3уравнениях а=0, в 4 уравнении нет свободного члена с,в 5,6 уравнениях нет в.
Учитель: А какие уравнения не приведенные и не неполные?
Ученики:например:6х²+3х+7=0, 8х²-4х-9=0, 0,5х²+2х – 9=0,
Вместо а любое число, кроме1 .
Учитель: Прочитайте в учебнике определение.
Определение на мультимедийной доске
Квадратным уравнением называется уравнение вида ах² +вх+ с =0, где х – переменная а,в и с – некоторые числа ,причем а ≠0.
4. Самостоятельная работа.( Задания на мультимедийной доске)
1) составить квадратное уравнение:
Первый коэффициент равен 12,коэффициентпри х равен 3,свободный член равен 2;
Первый член равен 8, второй член 5, свободный член равен 1.
Старший член равен5,свободный член раве7, втрой коэффициент равен -6.
Учитель : Поменяйтесь тетрадями, проверьте полученные уравнения.
Прочитаем ответы. Оцените друг друга.
А теперь решим уравнения .
Задания на мультимедийной доске.
Один ученик решает на доске, остальные в тетради
- Неполные квадратные уравнения
- Основные понятия
- Решение неполных квадратных уравнений
- Как решить уравнение ax² = 0
- Как решить уравнение ax² + с = 0
- Как решить уравнение ax² + bx = 0
- Презентация «Решение задач при помощи неполных квадратных уравнений» 8 класс
- Описание презентации по отдельным слайдам:
- Математика: теория и методика преподавания в образовательной организации
- Дистанционное обучение как современный формат преподавания
- Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 📸 Видео
Видео:Алгебра 8 класс (Урок№29 - Решение задач с помощью квадратных уравнений.)Скачать
Неполные квадратные уравнения
О чем эта статья:
Видео:Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать
Основные понятия
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.
Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:
- если D 0, есть два различных корня.
Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.
Неполные квадратные уравнения бывают трех видов:
Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать  Решение неполных квадратных уравненийКак мы уже знаем, есть три вида неполных квадратных уравнений:
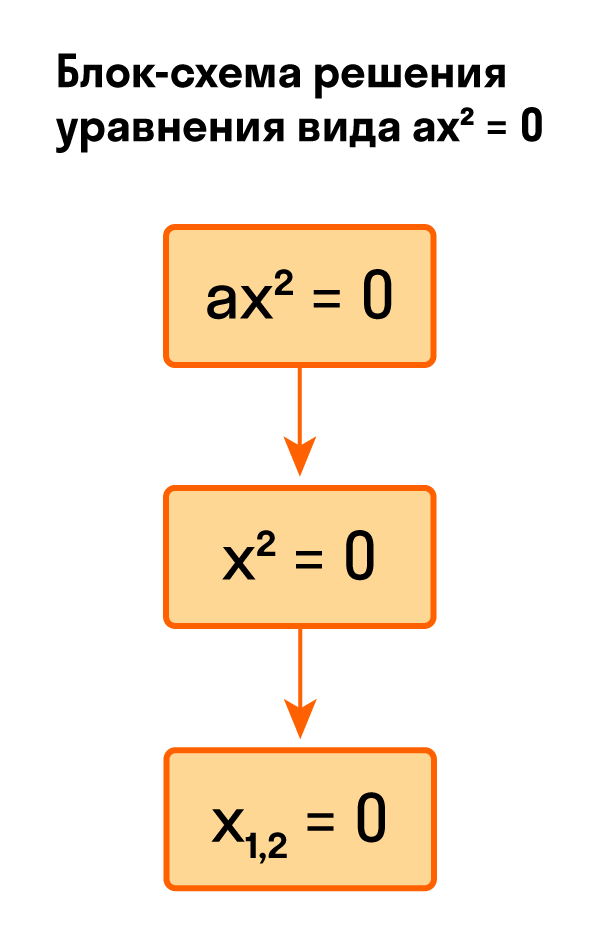
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль). Видео:АЛГЕБРА 8 класс : Решение неполных квадратных уравнений | ВидеоурокСкачать  Как решить уравнение ax² = 0Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0. Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней. Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0. Пример 1. Решить −5x² = 0.
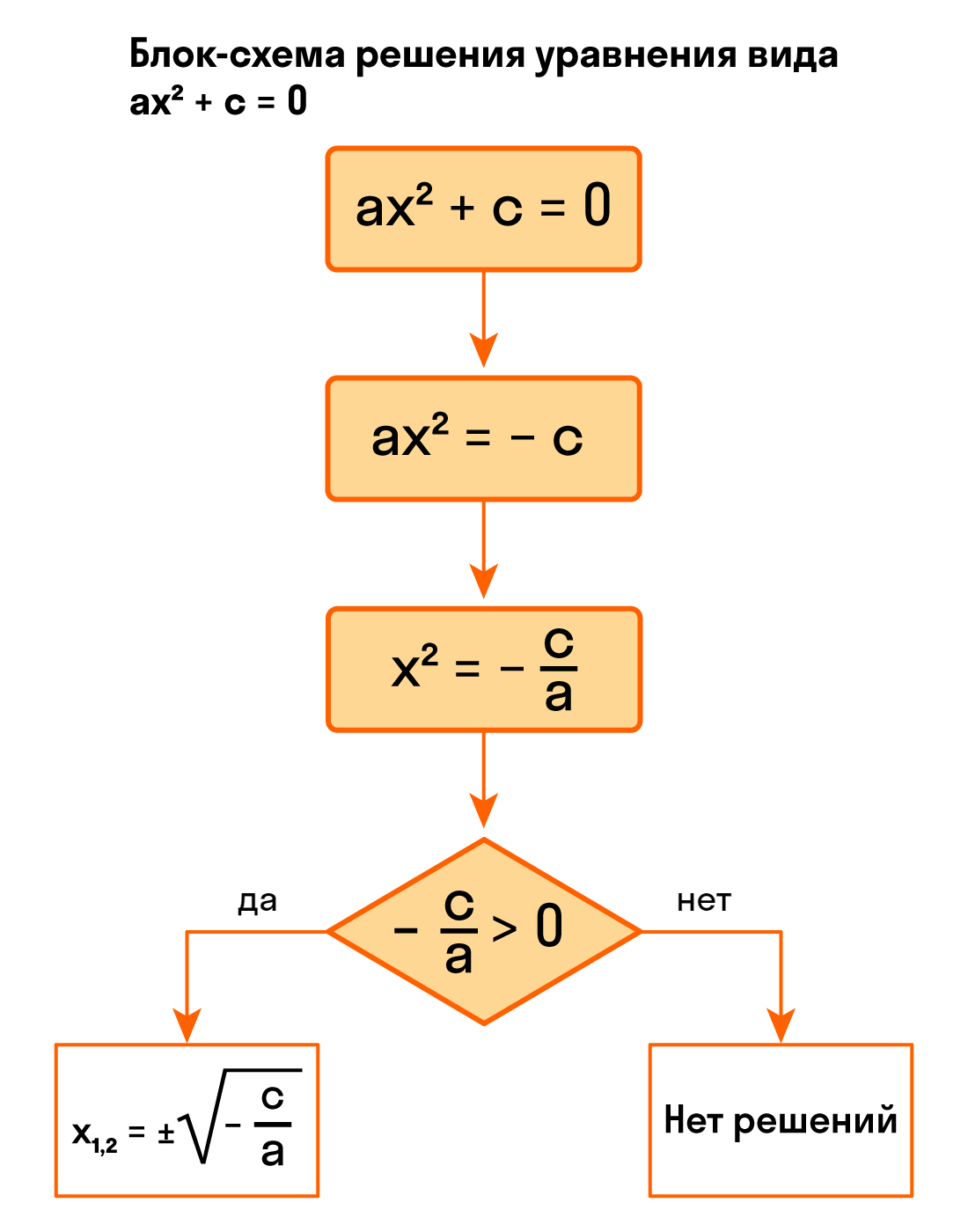
Записывайся на дополнительные уроки по математике онлайн, с нашими лучшими преподавателями! Для учеников с 1 по 11 класса! Видео:Урок 98 Решение текстовых задач с помощью квадратных уравнений (8 класс)Скачать  Как решить уравнение ax² + с = 0Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный. Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами. Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи. Если — c/а 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней. В двух словах квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое:
Пример 1. Найти решение уравнения 9x² + 4 = 0.
Разделим обе части на 9: Ответ: уравнение 9x² + 4 = 0 не имеет корней. Пример 2. Решить -x² + 9 = 0.
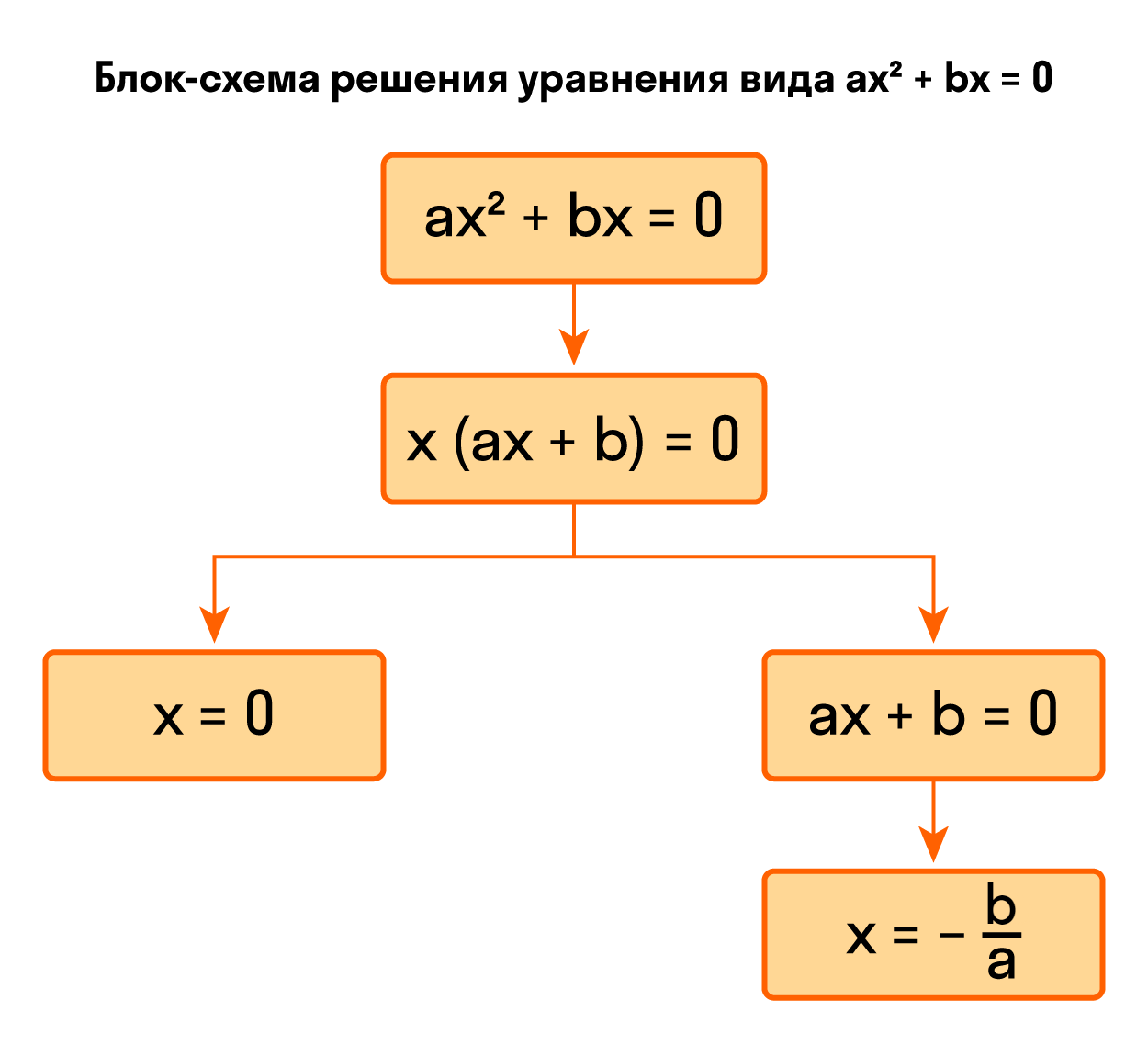
Разделим обе части на -1: Ответ: уравнение -x² + 9 = 0 имеет два корня -3; 3. Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать  Как решить уравнение ax² + bx = 0Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0. Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника. Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a. Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня: Пример 1. Решить уравнение 2x² — 32x = 0
Ответ: х = 0 и х = 16. Пример 2. Решить уравнение 3x² — 12x = 0 Разложить левую часть уравнения на множители и найти корни: Ответ: х = 0 и х = 4. Для удобства мы собрали все виды неполных квадратных уравнений и способы их решения на одной картинке-шпаргалке. Видео:Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать  Презентация «Решение задач при помощи неполных квадратных уравнений» 8 классОбращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах. Рабочие листы и материалы для учителей и воспитателей Более 300 дидактических материалов для школьного и домашнего обучения
Описание презентации по отдельным слайдам:
Решение задач при помощи неполных квадратных уравнений
Домашнее задание
Курс профессиональной переподготовки Математика: теория и методика преподавания в образовательной организации
Курс повышения квалификации Дистанционное обучение как современный формат преподавания
Курс повышения квалификации Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
«Мотивация здорового образа жизни. Организация секций» Свидетельство и скидка на обучение каждому участнику
«Как закрыть гештальт: практики и упражнения» Свидетельство и скидка на обучение каждому участнику Видео:Квадратное уравнение. 8 класс.Скачать  Дистанционные курсы для педагоговСамые массовые международные дистанционные Школьные Инфоконкурсы 2022 33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок» Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:5 843 574 материала в базе Материал подходит для УМК
«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А. Глава 3. Квадратные уравнения Ищем педагогов в команду «Инфоурок» Другие материалы
«Учись, играя: эффективное обучение иностранным языкам дошкольников» Свидетельство и скидка на обучение Вам будут интересны эти курсы:Оставьте свой комментарийАвторизуйтесь, чтобы задавать вопросы. Добавить в избранное
Настоящий материал опубликован пользователем Парецкая Олеся Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал. Автор материала
Московский институт профессиональной Видео:КВАДРАТНОЕ УРАВНЕНИЕ дискриминантСкачать  Дистанционные курсы |
