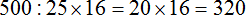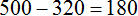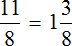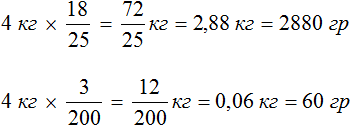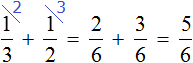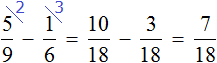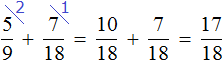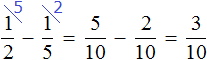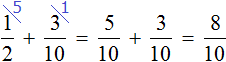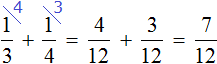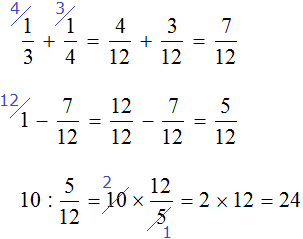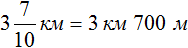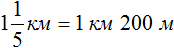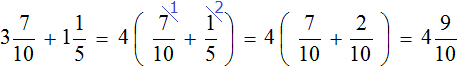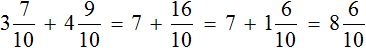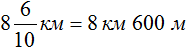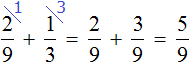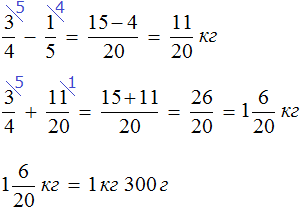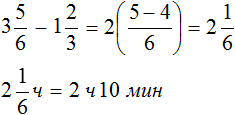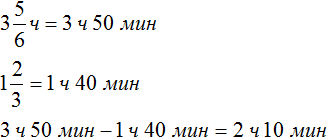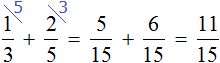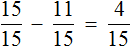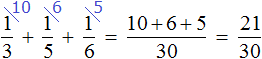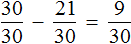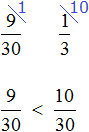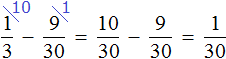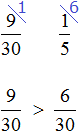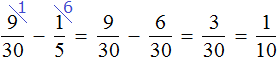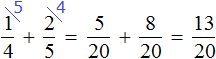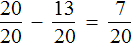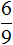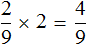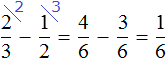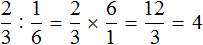Про уравнения - легко » Статьи

Решение задач по математике 5 класс дроби уравнения и задачи

Обновлено
Задачи на дроби

Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на дроби.

Прежде чем решать задачи на дроби, необходимо досконально изучить все темы, касающиеся дробей. Ниже приведен список уроков, которые можно повторить.

Каждая задача, приведенная в данном уроке, относится к категории элементарных. Если какая-то задача непонятна, это указывает на то, что предыдущий материал усвоен недостаточно хорошо.

Содержание
  1. Задачи на дроби
  2. Задачи для самостоятельного решения
  3. 30 thoughts on “Задачи на дроби”
  4. Решение задач уравнением. Задачи по математике для 5 класса.
  5. Задача 1
  6. Задача 2
  7. Задача 3
  8. Задача 4
  9. Задача 5
  10. Задача 6
  11. Задача 7
  12. Задача 8
  13. Задача 9
  14. Задача 10
  15. Задача 11
  16. Задача 12
  17. Презентация «Решение уравнений и задач по теме «Обыкновенные дроби»» (урок-сказка «Спасение похищенных чисел») презентация к уроку по математике (5 класс) на тему
  18. Презентация «Решение уравнений и задач по теме «Обыкновенные дроби»»
  19. (урок-сказка «Спасение похищенных чисел»)
  20. Скачать:
  21. Предварительный просмотр:
  22. Подписи к слайдам:
  23. 🌟 Видео

Видео:Уравнение. Практическая часть - решение задачи. 2 часть. 5 класс.Скачать

Уравнение. Практическая часть - решение задачи. 2 часть. 5 класс.

Задачи на дроби

Задача 1. В классе Решение задач по математике 5 класс дроби уравнения и задачишкольников составляют отличники. Какую часть составляют остальные? Сделать графическое описание задачи. Рисунок может быть любым.

Решение

Если Решение задач по математике 5 класс дроби уравнения и задачисоставляют отличники, то составляют остальные

Решение задач по математике 5 класс дроби уравнения и задачи

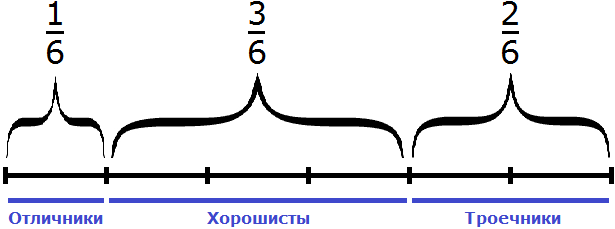
Задача 2. В классе школьников составляют отличники, Решение задач по математике 5 класс дроби уравнения и задачисоставляют хорошисты, Решение задач по математике 5 класс дроби уравнения и задачисоставляют троечники. Сделать графическое описание задачи. Рисунок может быть любым.

Решение задач по математике 5 класс дроби уравнения и задачи

Задача 3. В классе 24 школьника. школьников составляют отличники, Решение задач по математике 5 класс дроби уравнения и задачисоставляют хорошисты, Решение задач по математике 5 класс дроби уравнения и задачисоставляют троечники. Сколько в классе отличников, хорошистов и троечников?

Решение

24 : 6 × 1 = 4 × 1 = 4 (отличника)

24 : 6 × 3 = 4 × 3 = 12 (хорошистов)

24 : 6 × 2 = 4 × 2 = 8 (троечников)

Проверка

4 + 12 + 8 = 24 (школьника)

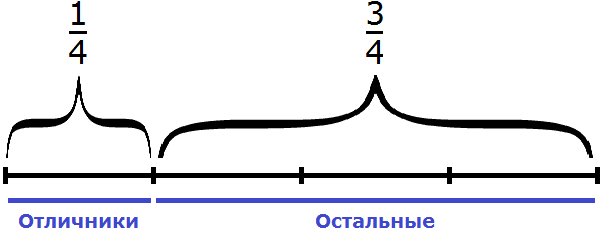
Задача 4. В классе школьников составляют отличники, Решение задач по математике 5 класс дроби уравнения и задачисоставляют хорошисты. Какую часть составляют троечники?

Решение

Школьники разделены на 6 частей. На одну из частей приходятся отличники, на три части — хорошисты. Нетрудно догадаться, что на остальные две части приходятся троечники. Значит Решение задач по математике 5 класс дроби уравнения и задачишкольников составляют троечники

Решение задач по математике 5 класс дроби уравнения и задачи

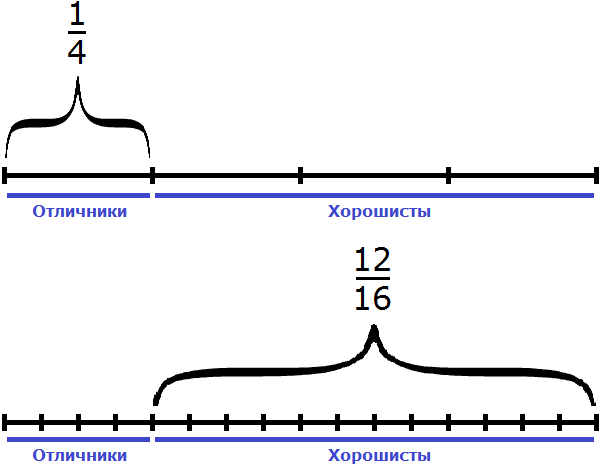
Не приводя рисунков можно сложить дроби и Решение задач по математике 5 класс дроби уравнения и задачи, и полученный результат вычесть из дроби Решение задач по математике 5 класс дроби уравнения и задачи, которая выражает всю часть школьников. Другими словами, сложить отличников и хорошистов, затем вычесть этих отличников и хорошистов из общего количества школьников

Решение задач по математике 5 класс дроби уравнения и задачи

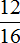
Задача 5. В классе 16 школьников. Из них Решение задач по математике 5 класс дроби уравнения и задачисоставляют отличники, Решение задач по математике 5 класс дроби уравнения и задачисоставляют хорошисты. Сколько отличников и хорошистов в классе? Сделать графическое описание задачи. Рисунок может быть любым.

Решение

16 : 4 × 1 = 4 × 1 = 4 (отличника)

16 : 16 × 12 = 1 × 12 = 12 (хорошистов)

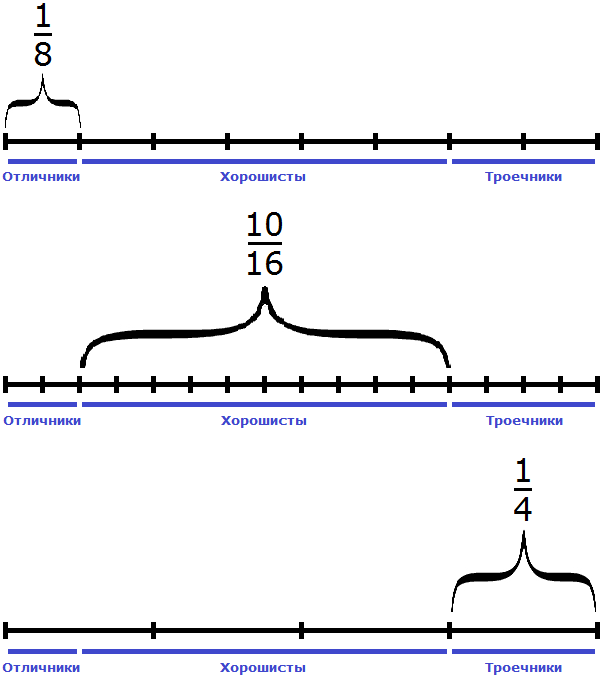
Решение задач по математике 5 класс дроби уравнения и задачи

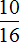
Задача 6. В классе 16 школьников. Из них Решение задач по математике 5 класс дроби уравнения и задачисоставляют отличники, Решение задач по математике 5 класс дроби уравнения и задачисоставляют хорошисты, Решение задач по математике 5 класс дроби уравнения и задачисоставляют троечники. Сколько отличников, хорошистов и троечников в классе? Сделать графическое описание задачи. Рисунок может быть любым.

Решение

16 : 8 × 1 = 2 × 1 = 2 (отличника)

16 : 16 × 10 = 1 × 10 = 10 (хорошистов)

16 : 4 = 4 (троечника)

Решение задач по математике 5 класс дроби уравнения и задачи

Задача 7. Из зерен пшеницы производят полтавскую крупу, масса которой составляет 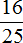Решение задач по математике 5 класс дроби уравнения и задачимассы зерна пшеницы, а остальное составляют кормовые отходы. Сколько можно получить полтавской крупы и кормовых отходов из 500 центнеров пшеницы

Решение

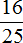
Найдем Решение задач по математике 5 класс дроби уравнения и задачиот 500 центнеров:

Решение задач по математике 5 класс дроби уравнения и задачи

Теперь найдем массу кормовых отходов. Для этого вычтем из 500 ц массу полтавской крупы:

Решение задач по математике 5 класс дроби уравнения и задачи

Значит из 500 центнеров зерен пшеницы можно получить 320 центнеров полтавской крупы и 180 центнеров кормовых отходов.

Задача 8. Килограмм сахара стоит 88 рублей. Сколько стоит Решение задач по математике 5 класс дроби уравнения и задачикг сахара? Решение задач по математике 5 класс дроби уравнения и задачикг? Решение задач по математике 5 класс дроби уравнения и задачикг? Решение задач по математике 5 класс дроби уравнения и задачикг?

Решение

1) Решение задач по математике 5 класс дроби уравнения и задачикг это половина одного килограмма. Если один килограмм стоит 88 рублей, то половина килограмма будет стоит половину от 88, то есть 44 рубля. Если найти половину от 88 рублей, мы получим 44 рубля

44 × 1 = 44 рубля

2) Решение задач по математике 5 класс дроби уравнения и задачикг это четверть килограмма. Если один килограмм стоит 88 рублей, то четверть килограмма будет стоит четверти от 88 рублей, то есть 22 рубля. Если найти Решение задач по математике 5 класс дроби уравнения и задачиот 88 рублей, мы получим 22 рубля

22 × 1 = 22 рубля

3) Дробь Решение задач по математике 5 класс дроби уравнения и задачиозначает, что килограмм разделен на восемь частей, и оттуда взято три части. Если один килограмм стоит 88 рублей, то стоимость трех восьми килограмм будут стоить Решение задач по математике 5 класс дроби уравнения и задачиот 88 рублей. Если найти Решение задач по математике 5 класс дроби уравнения и задачиот 88 рублей, мы получим 33 рубля.

4) Дробь Решение задач по математике 5 класс дроби уравнения и задачиозначает, что килограмм разделен на восемь частей, и оттуда взято одиннадцать частей. Но невозможно взять одиннадцать частей, если их только восемь. Мы имеем дело с неправильной дробью. Сначала выделим в ней целую часть:

Решение задач по математике 5 класс дроби уравнения и задачи

Одиннадцать восьмых это один целый килограмм и Решение задач по математике 5 класс дроби уравнения и задачикилограмма. Теперь мы можем по отдельности найти стоимость одного целого килограмма и стоимость трёх восьмых килограммов. Один килограмм, как было указано выше стоит 88 рублей. Стоимость Решение задач по математике 5 класс дроби уравнения и задачикг мы также находили и получили 33 рубля. Значит Решение задач по математике 5 класс дроби уравнения и задачикг сахара будет стоит 88+33 рубля, то есть 121 рубль.

Стоимость Решение задач по математике 5 класс дроби уравнения и задачиможно найти не выделяя целой части. Для этого достаточно найти Решение задач по математике 5 класс дроби уравнения и задачиот 88.

Но выделив целую часть можно хорошо понять, как сформировалась цена на Решение задач по математике 5 класс дроби уравнения и задачикг сахара.

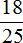
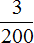
Задача 9. Финики содержат Решение задач по математике 5 класс дроби уравнения и задачисахара и Решение задач по математике 5 класс дроби уравнения и задачиминеральных солей. Сколько граммов каждого из веществ содержится в 4 кг фиников?

Решение

Узнаем сколько граммов сахара содержится в одном килограмме фиников. Один килограмм это тысяча грамм. Найдем 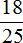Решение задач по математике 5 класс дроби уравнения и задачиот 1000 грамм:

В одном килограмме фиников содержится 720 грамм сахара. Чтобы узнать сколько грамм сахара содержится в четырех килограммах, нужно 720 умножить на 4

Теперь узнаем сколько минеральных солей содержится в 4 килограммах фиников. Но сначала узнаем сколько минеральных солей содержится в одном килограмме. Один килограмм это тысяча грамм. Найдем 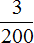Решение задач по математике 5 класс дроби уравнения и задачиот 1000 грамм:

В одном килограмме фиников содержится 15 грамм минеральных солей. Чтобы узнать сколько грамм минеральных солей содержится в четырех килограммах, нужно 15 умножить на 4

Значит в 4 кг фиников содержится 2880 грамм сахара и 60 грамм минеральных солей.

Решение для данной задачи можно записать значительно короче, двумя выражениями:

Решение задач по математике 5 класс дроби уравнения и задачи

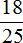
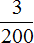
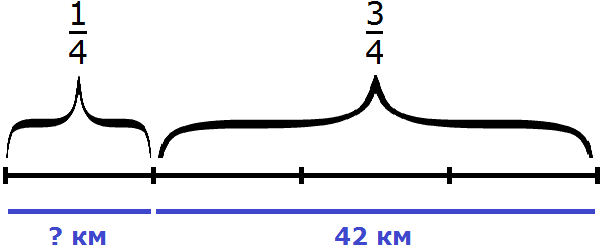
Суть в том, что от 4 килограмм нашли Решение задач по математике 5 класс дроби уравнения и задачии полученные 2,88 перевели в граммы, умножив на 1000. Тоже самое сделали и для минеральных солей — от 4 кг нашли Решение задач по математике 5 класс дроби уравнения и задачии получившиеся килограммы перевели в граммы, умножив на 1000. Обратите также внимание на то, что дробь от числа найдена упрощенным способом — прямым умножением числа на дробь.

Задача 10. Поезд прошел 840 км, что составляет Решение задач по математике 5 класс дроби уравнения и задачиего пути. Какое расстояние ему осталось пройти? Каково расстояние всего пути?

Решение

В задаче говорится, что 840 км это Решение задач по математике 5 класс дроби уравнения и задачиот его пути. Знаменатель дроби Решение задач по математике 5 класс дроби уравнения и задачиуказывает на то, что весь путь разделен на семь равных частей, а числитель указывает на то, что четыре части этого пути уже пройдено и составляют 840 км. Поэтому, разделив 840 км на 4, мы узнаем сколько километров приходится на одну часть:

А поскольку весь путь состоит из семи частей, то расстояние всего пути можно найти, умножив 210 на 7:

210 × 7 = 1470 км.

Теперь ответим на второй вопрос задачи — какое расстояние осталось пройти поезду? Если длина пути 1470 км, а пройдено 840, то оставшийся путь равен 1470−840, то есть 630

Задача 11. Одна из групп, покорившая горную вершину Эверест, состояла из спортсменов, проводников и носильщиков. Спортсменов в группе было 25, число проводников составляло Решение задач по математике 5 класс дроби уравнения и задачичисла спортсменов, а число спортсменов и проводников вместе лишь 9/140 числа носильщиков. Сколько было носильщиков в этой экспедиции?

Решение

Спортсменов группе 25. Проводников составляет Решение задач по математике 5 класс дроби уравнения и задачичисла спортсменов. Найдем Решение задач по математике 5 класс дроби уравнения и задачиот 25 и узнаем сколько в группе проводников:

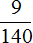
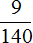
Спортсменов и проводников вместе — 45 человек. Это число составляет Решение задач по математике 5 класс дроби уравнения и задачиот числа носильщиков. Зная что Решение задач по математике 5 класс дроби уравнения и задачиот числа носильщиков это 45 человек, мы можем найти общее число носильщиков. Для этого найдем число по дроби:

45 : 9 × 140 = 5 × 140 = 700

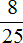
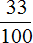
Задача 12. В школу привезли 900 новых учебников, из них учебники по математике составляли Решение задач по математике 5 класс дроби уравнения и задачивсех книг, учебники по русскому языку Решение задач по математике 5 класс дроби уравнения и задачивсех книг, а остальные книги были по литературе. Сколько привезли книг по литературе

Узнаем сколько составляют учебники по математике:

900 : 25 × 8 = 288 (книг по математике)

Узнаем сколько учебников по русскому языку:

900 : 100 × 33 = 297 (книг по русскому языку)

Узнаем сколько учебников по литературе. Для этого из общего числа книг вычтем учебники по математике и по русскому:

900 – (288+297) = 900 – 585 = 315

Проверка

288 + 297 + 315 = 900

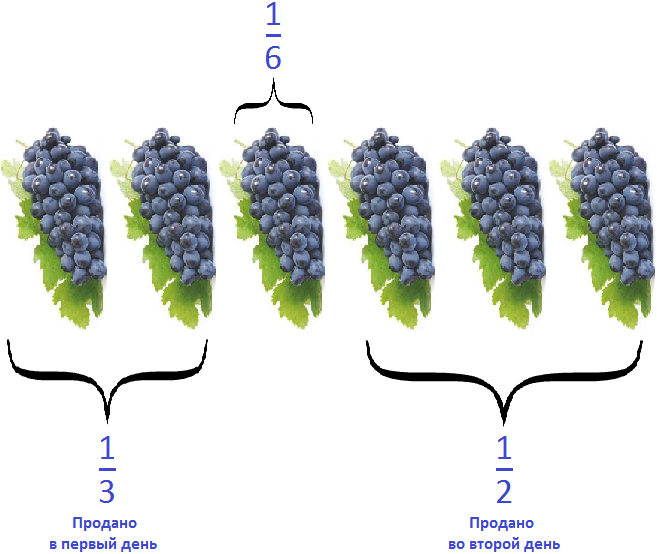
Задача 13. В первый день продали Решение задач по математике 5 класс дроби уравнения и задачи, а во второй день Решение задач по математике 5 класс дроби уравнения и задачипоступившего в магазин винограда. Какую часть винограда продали за два дня?

Решение

За два дня продали Решение задач по математике 5 класс дроби уравнения и задачивинограда. Эта часть получается путем сложения дробей Решение задач по математике 5 класс дроби уравнения и задачии Решение задач по математике 5 класс дроби уравнения и задачи

Решение задач по математике 5 класс дроби уравнения и задачи

Можно представить поступивший в магазин виноград в виде шести гроздей. Тогда Решение задач по математике 5 класс дроби уравнения и задачивинограда это две грозди, Решение задач по математике 5 класс дроби уравнения и задачивинограда — три грозди, а Решение задач по математике 5 класс дроби уравнения и задачивинограда это пять гроздей из шести, проданные за два дня. Ну и нетрудно увидеть, что осталась одна гроздь, выраженная дробь (одна гроздь из шести)

Решение задач по математике 5 класс дроби уравнения и задачи

Задача 14. Вера в первый день прочитала Решение задач по математике 5 класс дроби уравнения и задачикниги, а во второй день на меньше. Какую часть книги прочитала Вера во второй день? Успела ли она прочитать книгу за два дня?

Решение

Определим часть книги, прочитанной во второй день. Сказано, что во второй день прочитано на меньше, чем в первый день. Поэтому из Решение задач по математике 5 класс дроби уравнения и задачинужно вычесть

Решение задач по математике 5 класс дроби уравнения и задачи

Во второй день Вера прочитала 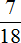Решение задач по математике 5 класс дроби уравнения и задачикниги. Теперь ответим на второй вопрос задачи — успела ли Вера прочитать книгу за два дня? Сложим то, что Вера прочитала в первый и во второй день:

Решение задач по математике 5 класс дроби уравнения и задачи

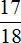
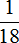
За два дня Вера прочитала Решение задач по математике 5 класс дроби уравнения и задачикниги, но осталось ещё Решение задач по математике 5 класс дроби уравнения и задачикниги. Значит Вера не успела прочитать всю книгу за два дня.

Сделаем проверку. Предположим что книга, которую читала Вера, имела 180 страниц. В первый день она прочла Решение задач по математике 5 класс дроби уравнения и задачикниги. Найдем Решение задач по математике 5 класс дроби уравнения и задачиот 180 страниц

180 : 9 × 5 = 100 (страниц)

Во второй день Вера прочитала на меньше, чем в первый. Найдем от 180 страниц, и вычтем полученный результат из 100 листов, прочитанных в первый день

180 : 6 × 1 = 30 × 1 = 30 (страниц)

100 − 30 = 70 (страниц во второй день)

Проверим, являются ли 70 страниц 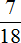Решение задач по математике 5 класс дроби уравнения и задачичастью книги:

180 : 18 × 7 = 10 × 7 = 70 (страниц)

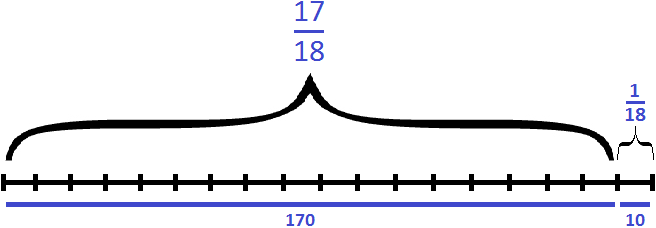
Теперь ответим на второй вопрос задачи — успела ли Вера прочитать все 180 страниц за два дня. Ответ — не успела, поскольку за два дня она прочла только 170 страниц

100 + 70 = 170 (страниц)

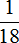
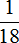
Осталось прочесть еще 10 страниц. В задаче в роли остатка у нас была дробь Решение задач по математике 5 класс дроби уравнения и задачи. Проверим являются ли 10 страниц Решение задач по математике 5 класс дроби уравнения и задачичастью книги?

180 : 18 × 1 = 10 × 1 = 10 (страниц)

Решение задач по математике 5 класс дроби уравнения и задачи

Задача 15. В одном пакете Решение задач по математике 5 класс дроби уравнения и задачикг, а в другом на Решение задач по математике 5 класс дроби уравнения и задачикг меньше. Сколько килограммов конфет в двух пакетах вместе?

Решение

Определим массу второго пакета. Она на Решение задач по математике 5 класс дроби уравнения и задачикг меньше, чем масса первого пакета. Поэтому из массы первого пакета вычтем массу второго:

Решение задач по математике 5 класс дроби уравнения и задачи

Масса второго пакета 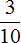Решение задач по математике 5 класс дроби уравнения и задачикг. Определим массу обоих пакетов. Сложим массу первого и массу второго:

Решение задач по математике 5 класс дроби уравнения и задачи

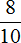
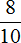
Масса обоих пакетов Решение задач по математике 5 класс дроби уравнения и задачикг. А Решение задач по математике 5 класс дроби уравнения и задачикилограмма это 800 граммов. Можно решать такую задачу, работая с дробями, складывая и вычитая их. Также можно сначала найти число по данным в задаче дробям и приступить к решению. Так Решение задач по математике 5 класс дроби уравнения и задачикилограмма это 500 граммов, а Решение задач по математике 5 класс дроби уравнения и задачикг это 200 граммов

1000 : 2 × 1 = 500 × 1 = 500 г

1000 : 5 × 1 = 200 × 1 = 200 г

Во втором пакете на 200 граммов меньше, поэтому чтобы определить массу второго пакета, нужно из 500 г вычесть 200 г

500 − 200 = 300 г

Ну и напоследок сложить массы обоих пакетов:

500 + 300 = 800 г

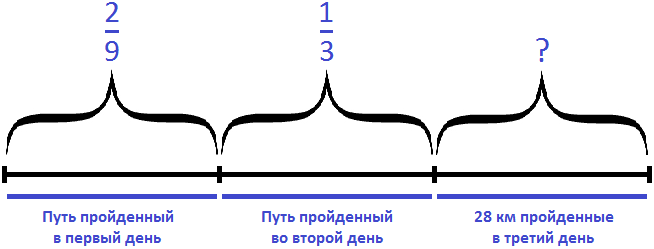
Задача 16. Туристы прошли путь от турбазы до озера за 4 дня. В первый день они прошли Решение задач по математике 5 класс дроби уравнения и задачивсего пути, во второй Решение задач по математике 5 класс дроби уравнения и задачиоставшегося пути, а в третий и четвертый дни проходили по 12 км. Чему равна длина всего пути от турбазы до озера?

Решение

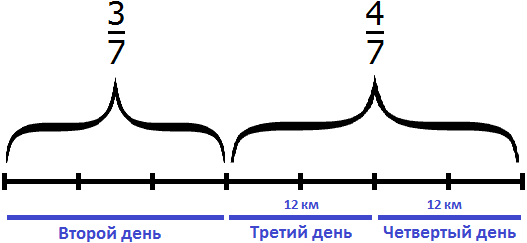
В задаче сказано, что во второй день туристы прошли Решение задач по математике 5 класс дроби уравнения и задачиоставшегося пути . Дробь Решение задач по математике 5 класс дроби уравнения и задачиозначает, что оставшийся путь разделен на 7 равных частей, из них туристы прошли три части, но осталось пройти остальные Решение задач по математике 5 класс дроби уравнения и задачи. На эти Решение задач по математике 5 класс дроби уравнения и задачиприходится то расстояние, которое туристы прошли в третий и четвертый день, то есть 24 км (по 12 км в каждом дне). Нарисуем наглядную схему, иллюстрирующую второй, третий и четвертый дни:

Решение задач по математике 5 класс дроби уравнения и задачи

В третий и четвертый день туристы прошли 24 км и это составляет Решение задач по математике 5 класс дроби уравнения и задачиот пути, пройденного во второй, третий и четвертый дни. Зная, что Решение задач по математике 5 класс дроби уравнения и задачисоставляют 24 км, мы можем найти весь путь, пройденный во второй, третий и четвертый день:

24 : 4 × 7 = 6 × 7 = 42 км

Во второй, третий и четвертый день туристы прошли 42 км. Теперь найдем Решение задач по математике 5 класс дроби уравнения и задачиот этого пути. Так мы узнаем сколько километров туристы прошли во второй день:

42 : 7 × 3 = 6 × 3 = 18 км

Теперь возвращаемся к началу задачи. Сказано, что в первый день туристы прошли Решение задач по математике 5 класс дроби уравнения и задачивсего пути. Весь путь разделен на четыре части, и на первую часть приходится путь, пройденный в первый день. А путь, который приходится на остальные три части, мы уже нашли — это 42 километра, пройденные во второй, третий и четвертый дни. Нарисуем наглядную схему, иллюстрирующую первый и остальные три дня:

Решение задач по математике 5 класс дроби уравнения и задачи

Зная, что пути составляют 42 километра, мы можем найти длину всего пути:

42 : 3 × 4 = 56 км

Значит длина пути от турбазы до озера составляет 56 километров. Сделаем проверку. Для этого сложим все пути, пройденные туристами в каждый из четырех дней.

Сначала найдем путь пройденный в первый день:

56 : 4 × 1 = 14 (в первый день)

14 + 18 + 12 + 12 = 56

Задача из арифметики известного среднеазиатского математика Мухаммеда ибн-Мусы ал-Хорезми (IX век н. э.)

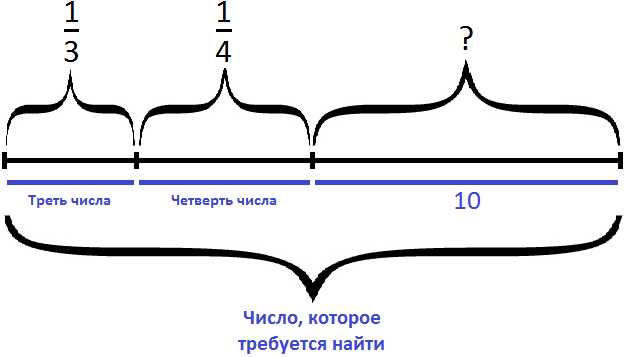
«Найти число, зная, что если отнять от него одну треть и одну четверть, то получится 10»

Изобразим число, которое мы хотим найти, в виде отрезка, разделенного на три части. В первой части отрезка отметим треть, во второй — четверть, оставшаяся третья часть будет изображать число 10.

Решение задач по математике 5 класс дроби уравнения и задачи

Сложим треть и четверть:

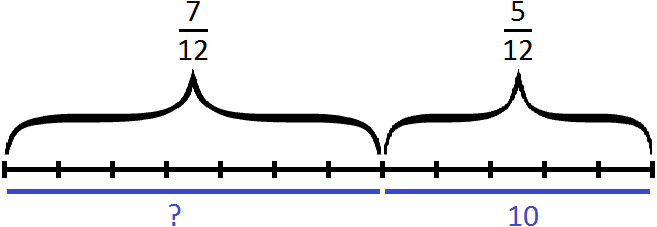
Решение задач по математике 5 класс дроби уравнения и задачи

Теперь изобразим отрезок, разделенный на 12 частей. Отметим на нем дробь 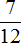Решение задач по математике 5 класс дроби уравнения и задачи, остальные пять частей пойдут на число 10:

Решение задач по математике 5 класс дроби уравнения и задачи

Зная, что пять двенадцатых числа составляют число 10, мы можем найти всё число:

10 : 5 × 12 = 2 × 12 = 24

Мы нашли всё число — оно равно 24.

Эту задачу можно решить не приводя рисунков. Для этого, сначала нужно сложить треть и четверть. Затем из единицы, которая играет роль неизвестного числа, вычесть результат сложения трети и четверти. Затем по полученной дроби определить всё число:

Решение задач по математике 5 класс дроби уравнения и задачи

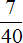
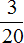
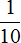
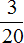
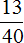
Задача 17. Семья, состоящая из четырех человек, в месяц зарабатывает 80 тысяч рублей. Бюджет распланирован следующим образом: Решение задач по математике 5 класс дроби уравнения и задачина еду, Решение задач по математике 5 класс дроби уравнения и задачина коммунальные услуги, Решение задач по математике 5 класс дроби уравнения и задачина Интернет и ТВ, Решение задач по математике 5 класс дроби уравнения и задачина лечение и походы по врачам, Решение задач по математике 5 класс дроби уравнения и задачина пожертвование в детский дом, Решение задач по математике 5 класс дроби уравнения и задачина проживание в съемной квартире, Решение задач по математике 5 класс дроби уравнения и задачив копилку. Сколько денег выделено на еду, коммунальные услуги, на Интернет и ТВ, на лечение и походы по врачам, пожертвование на детский дом, на проживание в съемной квартире, и на копилку?

Решение

80 : 40 × 7 = 14 (тыс. на еду)

80 : 20 × 1 = 4 × 1 = 4 тыс. (на коммунальные услуги)

80 : 20 × 1 = 4 × 1 = 4 тыс. (на Интернет и ТВ)

80 : 20 × 3 = 4 × 3 = 12 тыс. (на лечение и походы по врачам)

80 : 10 × 1 = 8 × 1 = 8 тыс. (на пожертвование в детский дом)

80 : 20 × 3 = 4 × 3 = 12 тыс. (на проживание в съемной квартире)

80 : 40 × 13 = 2 × 13 = 26 тыс. (в копилку)

Проверка

14 + 4 + 4 + 12 + 8 + 12 + 26 = 80

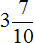
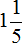
Задача 18. Туристы во время похода за первый час прошли Решение задач по математике 5 класс дроби уравнения и задачикм, а за второй на Решение задач по математике 5 класс дроби уравнения и задачикм больше. Сколько километров прошли туристы за два часа?

Решение

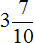
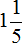
Найдем числа по дробям. Решение задач по математике 5 класс дроби уравнения и задачиэто три целых километра и семь десятых километра, а семь десятых километра это 700 метров:

Решение задач по математике 5 класс дроби уравнения и задачи

Решение задач по математике 5 класс дроби уравнения и задачиэто один целый километр и одна пятая километра, а одна пятая километра это 200 метров

Решение задач по математике 5 класс дроби уравнения и задачи

Определим длину пути, пройденного туристами за второй час. Для этого к 3 км 700 м нужно прибавить 1 км 200 м

3 км 700 м + 1 км 200 м = 3700м + 1200м = 4900м = 4 км 900 м

Определим длину пути, пройденного туристами за два часа:

3 км 700 м + 4 км 900 = 3700м + 4900м = 8600м = 8 км 600 м

Значит за два часа туристы прошли 8 километров и еще 600 метров. Решим эту задачу с помощью дробей. Так её можно значительно укоротить

Решение задач по математике 5 класс дроби уравнения и задачи

Решение задач по математике 5 класс дроби уравнения и задачи

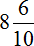
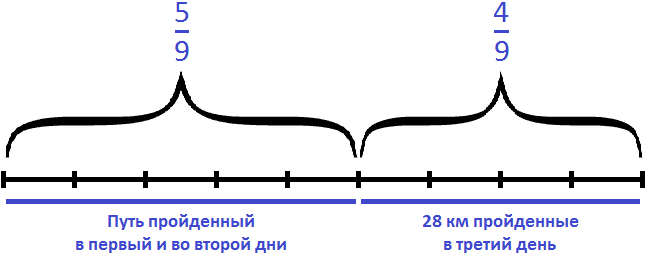
Получили ответ Решение задач по математике 5 класс дроби уравнения и задачикилометра. Это восемь целых километров и шесть десятых километра, а шесть десятых километра это шестьсот метров

Решение задач по математике 5 класс дроби уравнения и задачи

Задача 19. Геологи прошли долину, расположенную между горами, за три дня. В первый день они прошли Решение задач по математике 5 класс дроби уравнения и задачи, во второй Решение задач по математике 5 класс дроби уравнения и задачивсего пути и в третий оставшиеся 28 км. Вычислить длину пути, проходящего по долине.

Решение

Изобразим путь в виде отрезка, разделенного на три части. В первой части отметим Решение задач по математике 5 класс дроби уравнения и задачипути, во второй части Решение задач по математике 5 класс дроби уравнения и задачипути, в третьей части оставшиеся 28 километров:

Решение задач по математике 5 класс дроби уравнения и задачи

Сложим части пути, пройденные в первый и во второй день:

Решение задач по математике 5 класс дроби уравнения и задачи

За первый и второй дни геологи прошли Решение задач по математике 5 класс дроби уравнения и задачивсего пути. На остальные Решение задач по математике 5 класс дроби уравнения и задачипути приходятся 28 километров, пройденные геологами в третий день. Зная, что 28 километров это Решение задач по математике 5 класс дроби уравнения и задачивсего пути, мы можем найти длину пути, проходящего по долине:

28 : 4 × 9 = 7 × 9 = 63 км

Решение задач по математике 5 класс дроби уравнения и задачи

Проверка

63 : 9 × 5 = 7 × 5 = 35

63 : 9 × 4 = 7 × 4 = 28

Задача 20. Для приготовления крема использовали сливки, сметану и сахарную пудру. Сметану и сливки составляют 844,76 кг, а сахарная пудра и сливки 739,1 кг. Сколько в отдельности сливок, сметаны и сахарной пудры содержится в 1020,85 кг крема?

Решение

сметана и сливки — 844,76 кг
сахарная пудра и сливки — 739,1 кг

Вытащим из 1020,85 кг крема сметану и сливки (844,76 кг). Так мы найдем массу сахарной пудры:

1020,85 кг — 844,76 кг = 176,09 (кг сахарной пудры)

Вытащим из сахарной пудры и сливок сахарную пудру (176,09 кг). Так мы найдем массу сливок:

739,1 кг — 176,09 кг = 563,01 (кг сливок)

Вытащим сливки из сметаны и сливок. Так мы найдем массу сметаны:

844,76 кг — 563,01 кг = 281,75 (кг сметаны)

176,09 (кг сахарная пудра)

563,01 (кг сливки)

281,75 (кг сметана)

Проверка

176,09 кг + 563,01 кг + 281,75 кг = 1020,85 кг

1020,85 кг = 1020,85 кг

Задача 21. Масса бидона, заполненного молоком равна 34 кг. Масса бидона, заполненного наполовину, равна 17,75 кг. Какова масса пустого бидона?

Решение

Вычтем из массы бидона, заполненного молоком, массу бидона заполненного наполовину. Так мы получим массу содержимого бидона, заполненного наполовину, но уже без учета массы бидона:

34 кг − 17,75 кг = 16,25 кг

16,25 это масса содержимого бидона заполненного наполовину. Умножим эту массу на 2, получим массу бидона заполненного полностью:

16,25 кг × 2 = 32,5 кг

32,5 кг это масса содержимого бидона. Чтобы вычислить массу пустого бидона, нужно из 34 кг вычесть массу его содержимого, то есть 32,5 кг

34 кг − 32,5 кг = 1,5 кг

Ответ: масса пустого бидона составляет 1,5 кг.

Задача 22. Сливки составляют 0,1 массы молока, а сливочное масло составляет 0,3 массы сливок. Сколько сливочного масла можно получить из суточного надоя коровы, равного 15 кг молока?

Решение

Определим сколько килограмм сливок можно получить с 15 кг молока. Для этого найдем 0,1 часть от 15 кг.

15 × 0,1 = 1,5 (кг сливок)

Теперь определим сколько сливочного масла можно получить с 1,5 кг сливок. Для этого найдем 0,3 часть от 1,5 кг

1,5 кг × 0,3 = 0,45 (кг сливочного масла)

Ответ: из 15 кг молока можно получить 0,45 кг сливочного масла.

Задача 23. 100 кг клея для линолеума содержат 55 кг асфальта, 15 кг канифоли, 5 кг олифы и 25 кг бензина. Какую часть этого клея образует каждая из его составляющих?

Решение

Представим, что 100 кг клея как 100 частей. Тогда на 55 частей приходится асфальт, на 15 частей — канифоль, на 5 частей — олифа, на 25 частей — бензин. Запишем эти части в виде дробей, и по возможности сократим получающиеся дроби:

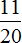
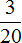
Решение задач по математике 5 класс дроби уравнения и задачи

Ответ: Решение задач по математике 5 класс дроби уравнения и задачиклея составляет асфальт, Решение задач по математике 5 класс дроби уравнения и задачисоставляет канифоль, Решение задач по математике 5 класс дроби уравнения и задачисоставляет олифа, Решение задач по математике 5 класс дроби уравнения и задачисоставляет бензин.

Видео:Математика 5 Обыкновенные дроби Основные задачи на дробиСкачать

Математика 5 Обыкновенные дроби Основные задачи на дроби

Задачи для самостоятельного решения

Решение

Решение задач по математике 5 класс дроби уравнения и задачи

Ответ: масса двух пакетов вместе составляет 1 кг 300 г

Решение

Решение задач по математике 5 класс дроби уравнения и задачи

Второй способ

Решение задач по математике 5 класс дроби уравнения и задачи

Ответ: театральное представление длилось 2 часа 10 минут.

Решение

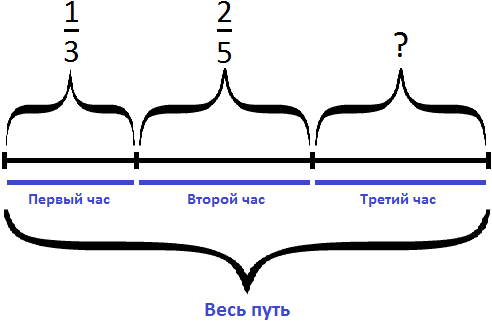
Решение задач по математике 5 класс дроби уравнения и задачи

Определим часть пути, пройденного лыжником за два часа движения. Для этого сложим дроби, выражающие пути пройденные за первый и второй час:

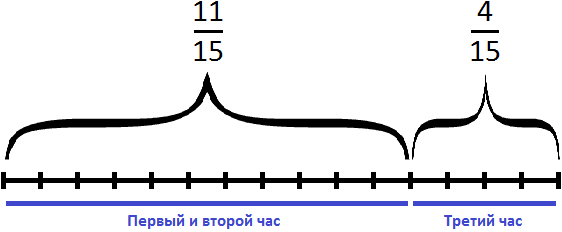
Решение задач по математике 5 класс дроби уравнения и задачи

Решение задач по математике 5 класс дроби уравнения и задачи

Определим часть пути, пройденного лыжником за третий час. Для этого из всех частей вычтем часть пути, пройденного за первый и второй час движения:

Решение задач по математике 5 класс дроби уравнения и задачи

Ответ: в третий час лыжник прошел Решение задач по математике 5 класс дроби уравнения и задачивсего расстояния.

Решение

Определим часть школьников, которые участвовали в футболе, баскетболе и в прыжках:

Решение задач по математике 5 класс дроби уравнения и задачи

Определим часть школьников, которые участвовали в беге:

Решение задач по математике 5 класс дроби уравнения и задачи

Узнаем на какую часть бегунов больше (или меньше) чем футболистов. Для начала сравним дроби 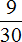Решение задач по математике 5 класс дроби уравнения и задачии Решение задач по математике 5 класс дроби уравнения и задачи

Решение задач по математике 5 класс дроби уравнения и задачи

Требовалось узнать на какую часть бегунов больше (или меньше) чем футболистов. Мы выяснили, что бегунов меньше, чем футболистов. Выясним на какую часть их меньше:

Решение задач по математике 5 класс дроби уравнения и задачи

Бегунов меньше, чем футболистов на Решение задач по математике 5 класс дроби уравнения и задачичасть.

Теперь узнаем на какую часть бегунов больше (или меньше) чем баскетболистов. Для начала сравним дроби 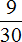Решение задач по математике 5 класс дроби уравнения и задачии Решение задач по математике 5 класс дроби уравнения и задачи

Решение задач по математике 5 класс дроби уравнения и задачи

Требовалось узнать на какую часть бегунов больше (или меньше) чем баскетболистов. Мы выяснили, что бегунов больше, чем баскетболистов. Выясним на какую часть их больше:

Решение задач по математике 5 класс дроби уравнения и задачи

Бегунов больше, чем баскетболистов на часть.

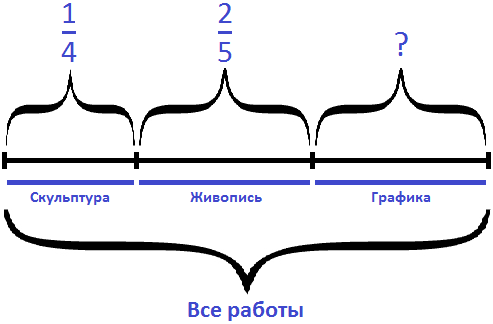
Ответ: бегунов было на Решение задач по математике 5 класс дроби уравнения и задачичасть меньше, чем футболистов и на часть больше, чем баскетболистов.

Задача 5. На выставке художественных работ представлена живопись, скульптура и графика. Решение задач по математике 5 класс дроби уравнения и задачивсех работ составляет скульптура, Решение задач по математике 5 класс дроби уравнения и задачи– живопись, оставшуюся часть – графика. Какую часть всех работ составляет графика?

Решение

Решение задач по математике 5 класс дроби уравнения и задачи

Сложим дроби, выражающие скульптуру и живопись:

Решение задач по математике 5 класс дроби уравнения и задачи

Определим какую часть всех работ составляет графика:

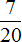
Решение задач по математике 5 класс дроби уравнения и задачи

Ответ: Решение задач по математике 5 класс дроби уравнения и задачивсех работ составляет графика.

Задача 6. Рабочие отремонтировали дорогу длиной 820 м за три дня. Во вторник они отремонтировали Решение задач по математике 5 класс дроби уравнения и задачиэтой дороги, а в среду оставшейся части. Сколько метров дороги отремонтировали рабочие в четверг?

Решение

Определим длину дороги, отремонтированной во вторник:

820 : 5 × 2 = 328 м

Определим длину дороги, отремонтированной в среду. Известно, что в этот день рабочие отремонтировали оставшейся дороги. Оставшаяся дорога это 820−328, то есть 492

492 : 3 × 2 = 328 м

Определим длину дороги, отремонтированной в четверг. Для этого вычтем из 820 длины дорог, отремонтированных во вторник и в среду:

820 − (328 + 328) = 820 − 656 = 164 м

Ответ: в четверг рабочие отремонтировали 164 метра дороги.

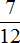
Задача 7. В книге три рассказа. Наташа прочла первый рассказ за Решение задач по математике 5 класс дроби уравнения и задачич, на чтение второго рассказа она потратила на ч больше, а чтение третьего рассказа заняло на Решение задач по математике 5 класс дроби уравнения и задачич меньше, чем чтение первого и второго рассказов вместе. Сколько времени ушло у Наташи на чтение всей книги?

Решение

Определим время за которое Наташа прочитала первый рассказ. Она прочила его за треть часа. Треть часа это 20 минут

60 : 3 × 1 = 20 минут

Определим время за которое Наташа прочитала второй рассказ. Она прочила его на ч больше. часа это 10 минут. Прибавим к 20 минутам 10 минут, получим время чтения второго рассказа:

20 + 10 = 30 минут

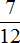
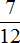
Определим время за которое Наташа прочитала третий рассказ. Она прочитала его на Решение задач по математике 5 класс дроби уравнения и задачич меньше, чем чтение первого и второго рассказов вместе. Решение задач по математике 5 класс дроби уравнения и задачичаса это 35 минут. Вычтем 35 из времени, затраченного на чтение первого и второго рассказа вместе (50 м)

Определим сколько времени ушло у Наташи на чтение всей книги:

20 + 30 + 15 = 65 минут = 1 ч 5 минут

На чтение всей книги у Наташи ушел 1 час и 5 минут. Решим эту задачу с помощью дробей. Так ее можно значительно укоротить:

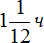
Решение задач по математике 5 класс дроби уравнения и задачи

Решение задач по математике 5 класс дроби уравнения и задачиэто один целый час и Решение задач по математике 5 класс дроби уравнения и задачичаса, а одну двенадцатую часа составляют 5 минут.

Ответ: на чтение всей книги у Наташи ушло Решение задач по математике 5 класс дроби уравнения и задачи

Задача 8. Из одной тонны хлопка-сырца можно изготовить 3400 м ткани, 1,05 ц пищевого масла и 0,225 т жмыха. Сколько метров ткани, пищевого масла и жмыха можно получить из 32,4 ц хлопка-сырца?

Решение

Переведем 32,4 ц в тонны. Одна тонна составляет 10 центнеров. Чтобы узнать сколько таких десять центнеров (имеется ввиду тонн) в 32,4 центнерах, нужно 32,4 разделить на 10

Определим сколько метров ткани можно получить с 3,24 тонн хлопка-сырца. С одной тонны, как указано в задаче, получается 3400 метров ткани. А с 3,24 тонн будет получено в 3,24 раза больше ткани

3400 × 3,24 = 11016 метров ткани.

Определим сколько пищевого масла можно получить с 3,24 тонн хлопка-сырца. С одной тонны, как указано в задаче, получается 1,05 ц пищевого масла. А с 3,24 тонн будет получено в 3,24 раза больше масла

1,05 × 3,24 = 3,402 центнера пищевого масла

Определим сколько жмыха можно получить с 3,24 тонн хлопка-сырца. С одной тонны, как указано в задаче, получается 0,225 т жмыха. А с 3,24 тонн будет получено в 3,24 раза больше жмыха

0,225 × 3,24 = 0,729 тонн жмыха

Ответ: из 32,4 ц хлопка сырца можно получить 11016 метров ткани, 3,402 ц пищевого масла и 0,729 т жмыха.

Решение

Зная, что 0,2 всего пути составляют 12 км, мы можем найти весь путь. Чтобы найти неизвестное число по десятичной дроби, нужно известное число разделить на десятичную дробь

Ответ: Туристы прошли 60 км.

Решение

Зная, что 0,7 книги составляют 56 страниц, мы можем узнать сколько всего страниц в книге. Чтобы найти неизвестное число по десятичной дроби, нужно известное число разделить на десятичную дробь

56 : 0,7 = 80 (страниц всего)

Узнаем сколько осталось прочитать

80 − 56 = 24 (страницы осталось прочитать)

Ответ: в книге 80 страниц. Прочитать осталось еще 24 страницы.

Решение

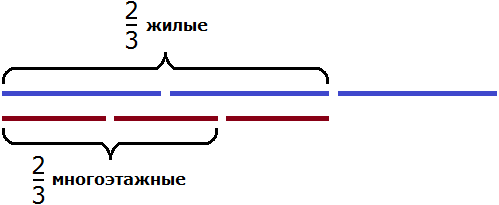
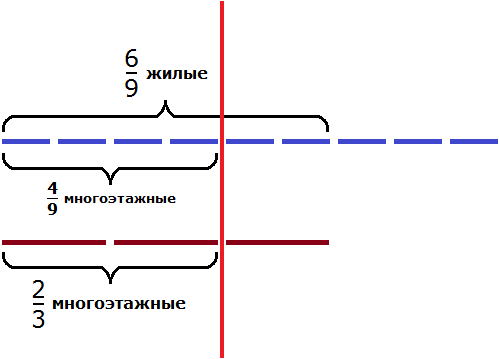
Решение задач по математике 5 класс дроби уравнения и задачи

Разделим жилых домов на три части:

Решение задач по математике 5 класс дроби уравнения и задачи

Теперь на треть многоэтажных домов приходится 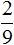Решение задач по математике 5 класс дроби уравнения и задачивсех зданий. Изначально все здания были разделены на три равные части. Теперь они разделены на девять равных частей. Жилые дома, которые ранее выражались дробью , теперь выражаются дробью Решение задач по математике 5 класс дроби уравнения и задачи

Решение задач по математике 5 класс дроби уравнения и задачи

Чтобы узнать сколько многоэтажных домов приходится на две трети, умножим 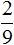Решение задач по математике 5 класс дроби уравнения и задачина 2

Решение задач по математике 5 класс дроби уравнения и задачи

Решение задач по математике 5 класс дроби уравнения и задачи

Ответ: жилые многоэтажные дома составляют 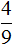Решение задач по математике 5 класс дроби уравнения и задачивсех зданий в городе.

Решение

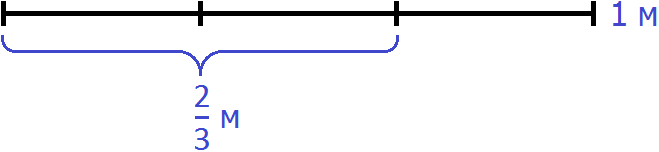
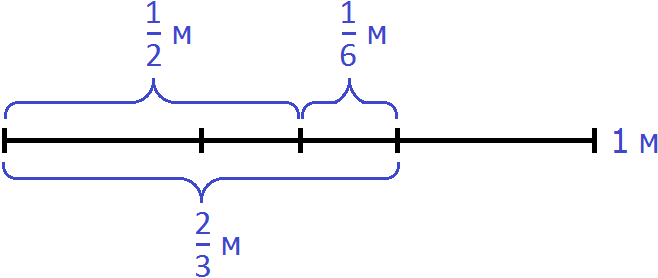
Изобразим схематически один метр веревки:

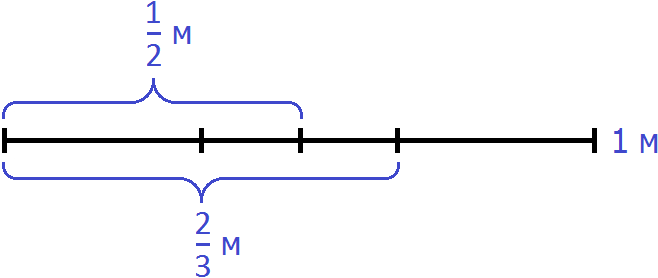
Решение задач по математике 5 класс дроби уравнения и задачи

Выделим на этом рисунке метра:

Решение задач по математике 5 класс дроби уравнения и задачи

Здесь же выделим Решение задач по математике 5 класс дроби уравнения и задачиметра

Решение задач по математике 5 класс дроби уравнения и задачи

Не выделенным на м остался один кусочек. Узнаем, что это за кусочек. Для этого из вычтем Решение задач по математике 5 класс дроби уравнения и задачи

Решение задач по математике 5 класс дроби уравнения и задачи

Решение задач по математике 5 класс дроби уравнения и задачи

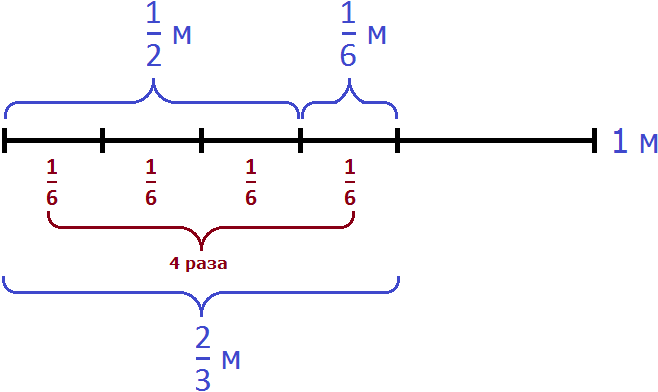
м это часть веревки, которую нужно отрезать. Тогда мы получим Решение задач по математике 5 класс дроби уравнения и задачим веревки.

Теперь осталось узнать сколько раз м содержит м

Решение задач по математике 5 класс дроби уравнения и задачи

Решение задач по математике 5 класс дроби уравнения и задачи

Значит, чтобы не производя измерений от м веревки отрезать Решение задач по математике 5 класс дроби уравнения и задачим, нужно эту веревку сложить вчетверо и отрезать одну часть. Оставшаяся часть и будет половиной от одного метра.

Ответ: чтобы от веревки, длина которой м отрезать Решение задач по математике 5 класс дроби уравнения и задачим, нужно сложить эту веревку вчетверо и отрезать от неё одну часть. Оставшаяся часть станет Решение задач по математике 5 класс дроби уравнения и задачим веревки.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Видео:Уравнение. Практическая часть - решение задачи. 1 часть. 5 класс.Скачать

Уравнение. Практическая часть - решение задачи. 1 часть. 5 класс.

30 thoughts on “Задачи на дроби”

Здравствуйте! Очень благодарна вам за ваши труды. Очень все доступно объясняете.
В задаче №2 есть опечатка. В условии одна целая пять шестых часа, а в решении одна целая две трети.

Добавлю, что задача №2 в разделе самостоятельного решения.

Здравствуйте! Спасибо вам большое за задачи!
Но я никак не могу понять, почему в 16 задаче такое решение. Почему 3/7 оставшегося пути не вычисляются из 24км? Ведь второй день = 3/7 оставшегося пути, этот путь равен 24км. Он не может включать и второй день? Разве нет?

24 км это путь, пройденный в третий и четвертый дни. А во второй день было пройдено совсем другое расстояние.

Вообще, во второй, третий и четвертый дни всего было пройдено 42 км.

Найдите от 42 км сначала 3/7 пути, а потом 4/7 пути. Сразу станет всё понятно 😉

А откуда в 3-й задаче взялась дробь 15 на 15?

Видео:Уравнение. 5 класс.Скачать

Уравнение. 5 класс.

Решение задач уравнением. Задачи по математике для 5 класса.

Задача 1

Лена загадала некоторое число. Если это число уменьшить на 12, то получится 5. Какое число загадала Лена?

    Решение
  • Пусть число, которое задумала Лена x. Тогда:
  • x – 12 = 5,
  • x = 12 + 5,
  • x = 17.
  • Ответ: Лена загадала число 17.

Задача 2

Некоторое число увеличили в 7 раз, после чего получили 119. Что это за число?

    Решение
  • Пусть y неизвестное число. Тогда:
  • 7y = 119,
  • y = 119 : 7,
  • y = 17.
  • Ответ: это число 17.

Задача 3

Найдите числа, следующие друг за другом, если их сумма равна 159.

    Решение
  • Пусть первое число равно x. Тогда:
  • x + x + 1 = 159,
  • 2x + 1 = 159,
  • 2x = 159 – 1 = 158,
  • x = 158 : 2,
  • x = 79,
  • x + 1 = 79 + 1 = 80.
  • Ответ: 79, 80.

Задача 4

Одно число больше другого на 38. Чему равны эти числа, если их сумма равна 184.

    Решение
  • Пусть меньшее число равно y. Тогда:
  • y + y + 38 = 184
  • 2y + 38 = 184,
  • 2y = 184 – 38 = 146,
  • y = 146 : 2 = 73,
  • y + 38 = 73 + 38 = 111.
  • Ответ: 111, 73.

Задача 5

За три дня турист преодолел 105 км. Сколько километров турист преодолел в первый день, если в каждый последующий день он преодолевал на 3 км больше, чем в предыдущий?

    Решение
  • Пусть в первый день турист преодолел x км. Тогда:
  • x + x + 3 + x + 3 + 3 = 105,
  • 3x + 9 = 105,
  • 3x = 105 – 9 = 96,
  • x = 96 : 3 = 32 (км).
  • Ответ: в первый день турист преодолел 32 км.

Задача 6

Сколько лет маме, если она старше дочери на 24 года, а дочь моложе матери в 7 раз?

    Решение
  • Пусть дочери x лет. Тогда:
  • x + 24 = 7x,
  • 24 = 7x – x,
  • 6x = 24,
  • x = 24 : 6 = 4,
  • x + 24 = 4 + 24 = 28.
  • Ответ: маме 28 лет.

Задача 7

На рисунке изображены треугольники и четырехугольники. Сколько тех и других изображено на рисунке, если у всех фигур вместе 69 углов, а всего фигур — 18?

    Решение
  • Пусть на рисунке изображено x четырехугольников. Тогда:
  • 4x + (18 – x) * 3 = 69,
  • 4x + 54 – 3x = 69,
  • x = 69 – 54 = 15,
  • 18 – x = 18 – 15 = 3.
  • Ответ: на рисунке было изображено 15 четырехугольников и 3 треугольников.

Задача 8

Швейная мастерская закупила 2 сорта ткани всего 49 метров. Стоимость одного 110 рублей за 1 метр, стоимость другого 100 рублей за 1 метр. Сколько метров каждого сорта было куплено, если всего потратили 5150 рублей?

    Решение
  • Пусть первого сорта ткани было закуплено x метров. Тогда:
  • 110x + (49 – x) * 100 = 5150,
  • 110x + 4900 – 100x = 5150,
  • 10x = 5150 – 4900 = 250,
  • x = 250 : 10 = 25,
  • x – 25 = 49 – 25 = 24.
  • Ответ: первого сорта ткани было куплено 25 метров, второго 24 метра.

Задача 9

Мама покупала в магазине овощи и фрукты. За овощи она заплатила на 90 рублей меньше чем за фрукты, а за фрукты заплатили в 2 раза больше, чем за овощи. Сколько мама заплатила за овощи и за фрукты по отдельности?

    Решение
  • Пусть за овощи мама заплатила x рублей. Тогда:
  • x + 90 = 2x,
  • x = 90,
  • 2x = 2 * 90 = 180 (рублей).
  • Ответ: за фрукты мама заплатила 180 рублей, за овощи 90 рублей.

Задача 10

Стоимость фломастеров и тетрадей вместе составляет 276 рублей, стоимость фломастеров составляет 0,6 стоимости книги, а тетради на 60 рублей дороже книги. Сколько стоят тетради?

    Решение
  • Пусть тетради стоят x рублей. Тогда:
  • (276 – x) : 0,6 – x = 60,
  • 276 – x = (60 + x) * 0,6,
  • 276 – x = 36 + 0,6x,
  • 1,6x = 276 – 36 = 240,
  • x = 240 : 1,6 = 150 (рублей).
  • Ответ: тетради стоят 150 рублей.

Задача 11

Саша задумал 3 натуральных числа. Первое из чисел наибольшее двузначное число, второе в 4 раза больше третьего. Что за числа задумал Саша, если сумма этих чисел равна 934?

    Решение
  • Наибольшее двузначное число – 99. Пусть третье число равно x. Тогда:
  • x + 4x + 99 = 934,
  • 5x = 934 – 99 = 835,
  • x = 835 : 5 = 167;
  • 4x = 4 * 167 = 668,
  • Ответ: Саша задумал числа 99, 167, 668.

Задача 12

На трех книжных полках стояли книги. На первой полке книг стояло в 2 раза меньше, чем на второй, а на третьей на 4 меньше чем на первой. Сколько книг стояло на каждой из полок, если всего в шкафу было 88 книг?

    Решение
  • Пусть на первой полке стояло x книг. Тогда:
  • x + 2x + x – 4 = 88,
  • 4x = 88 + 4 = 92,
  • x = 92 : 4 = 23 (книги) на первой полке;
  • 2x = 2 * 23 =46 (книг) на второй полке;
  • x – 4 = 23 – 4 = 19 (книг) на третьей.
  • Ответ: на первой полке стояло 23 книг, на второй 46, на третьей 19.

Видео:Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.

Презентация «Решение уравнений и задач по теме «Обыкновенные дроби»» (урок-сказка «Спасение похищенных чисел»)
презентация к уроку по математике (5 класс) на тему

Решение задач по математике 5 класс дроби уравнения и задачи

Видео:Обыкновенные дроби и действия над ними. Практическая часть. 5 класс.Скачать

Обыкновенные дроби и действия над ними. Практическая часть. 5 класс.

Презентация «Решение уравнений и задач по теме «Обыкновенные дроби»»

Видео:Урок 14 Решение задач с помощью уравнений (5 класс)Скачать

Урок 14 Решение задач с помощью уравнений (5 класс)

(урок-сказка «Спасение похищенных чисел»)

Видео:Как решать задачи по математике в 6 классе на части (дроби) с помощью уравнения и без уравнения.Скачать

Как решать задачи по математике в 6 классе на части (дроби) с помощью уравнения и без уравнения.

Скачать:

ВложениеРазмер
prezentatsiya1.ppt1.54 МБ

Предварительный просмотр:

Видео:Учимся дома. 5 класс. Математика: Задачи на частиСкачать

Учимся дома. 5 класс. Математика: Задачи на части

Подписи к слайдам:

Урок — сказка «Спасение похищенных чисел»

1 день – 4/7 от всего поля — это 28 га Всего — ?

725:29 ∙13=325(мужчин) 2) 725-325 =400 (женщин) Численность населения села Низовка 725 человек, 13/29 из них- мужчины. Сколько в селе женщин?

В библиотеку клуба поступило 200 новых книг и журналов. При этом этого количества составили журналы для взрослых и этого количества составили журналы для детей. Все остальные книги – художественные. Сколько художественных книг поступило в библиотеку? 2) 200:10 ∙ 6=120 (журн.) 3) 200-120=80 (книг) Ответ: В библиотеку поступило 80 художественных книг

№ 1 а) в) 23: 45= б) г) 7:56= № 2 Правильные дроби: Неправильные дроби:

Протяжённость нашей республики с запада на восток 280 км, а с севера на юг в среднем 93км. Найдите площадь Мордовии, если она занимает территорию, равную площади прямоугольника с такими сторонами.

Домашнее задание: П. 27, №1068(а),№ 1822, №1824

🌟 Видео

Уравнения с дробями. Как решать уравнения с дробями в 5 классе.Скачать

Уравнения с дробями. Как решать уравнения с дробями в 5 классе.

Уравнение с дробями видео урок ( Математика 5 класс )Скачать

Уравнение с дробями видео урок ( Математика 5 класс )

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?

ВСЯ математика 5-го класса в одном видео! Альфа-школаСкачать

ВСЯ математика 5-го класса в одном видео! Альфа-школа

Математика 6 класс (Урок№51 - Решение задач с помощью уравнений. Часть 1.)Скачать

Математика 6 класс (Урок№51 - Решение задач с помощью уравнений. Часть 1.)

Математика 5 класс (Урок№16 - Задачи «на части».)Скачать

Математика 5 класс (Урок№16 - Задачи «на части».)

Задача на нахождение части от числа. Как решать задачи с дробями?Скачать

Задача на нахождение части от числа. Как решать задачи с дробями?

как решать дробиСкачать

как решать дроби

Решение задач с помощью уравнений.Скачать

Решение задач с помощью уравнений.

Упрощение выражений. Практическая часть - решение задачи. 1 часть. 5 класс.Скачать

Упрощение выражений. Практическая часть - решение задачи. 1 часть. 5 класс.

Уравнения с дробями 5 класс (задания, примеры) - как решать?Скачать

Уравнения с дробями 5 класс (задания, примеры) - как решать?
Поделиться или сохранить к себе: