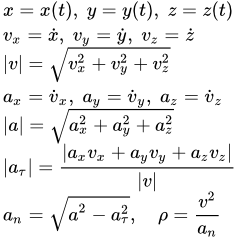- Теоретическая механика: Решебник Яблонского: Кинематика точки (К1)
- Задание К.1. Определение скорости и ускорения точки по заданным уравнениям ее движения
- Решение задач по кинематике
- Координатный способ задания движения точки
- Введение
- Определение кинематических величин
- Пример решения задачи
- Определение скорости и ускорения точки по заданным уравнениям ее движения
- Решение
- Определение вида траектории
- Определение скорости точки
- Определение ускорения точки
- Определение остальных величин
- 🔥 Видео
Теоретическая механика: Решебник Яблонского:
Кинематика точки (К1)
Бесплатный онлайн решебник Яблонского. Выберите задание и номер варианта для просмотра решения. Смотрите также способы и примеры решения задач по теме кинематика точки.
Видео:Кинематика материальной точки за 20 минут (кратко и доступно) Кинематика точкиСкачать

Задание К.1. Определение скорости и ускорения точки по заданным уравнениям ее движения
По заданным уравнениям движения точки M установить вид ее траектории и для момента времени t=t1 (c) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Необходимые для решения данные приведены в табл. 20.
Дополнение к заданию К.1. Данное задание может быть использовано для определения скорости и ускорения точки при ее движении по пространственной траектории. Для этого к двум уравнениям движения (см. табл. 20) добавляется третье уравнение (табл. 22).
Видео:Траектория и уравнения движения точки. Задача 1Скачать

Решение задач по кинематике
Решение задач по кинематике равнопеременного движения традиционно вызывает у учащихся затруднения, что связано в основном с тем, что здесь впервые встает проблема формализации физической задачи, т.е. перевода ее с языка “текстовой задачи” по физике на язык математики. До этого учащимся приходилось в основном решать задачи, если можно так выразиться, “по формулам”, а теперь необходимо осмыслить задачу не только с точки зрения физики, но и суметь записать ее в терминах уравнений кинематики и затем из этих уравнений, опираясь на условие задачи, получить нужные “формулы”. В настоящей работе представлен ход обзорного урока по этой теме.
Чтобы научиться решать задачи по кинематике нужно прежде всего уметь правильно выбрать систему отсчета (СО), которая включает в себя:
- Точку отсчета (выбираем произвольно из соображений удобства)
- Систему координат, связанную с точкой отсчета
- Начало отсчета времени (счетчик времени, выбираем из соображений удобства).
Вообще важно, чтобы учащиеся отдавали себе отчет, что для решения задач по кинематике необходимо:
Выбрать СО подходящим образом, чтобы в этой СО уравнения кинематики принимали наиболее простой вид. Обязательно обратить внимание на выбор начала отсчета времени.
Сделать чертеж, иллюстрирующий описанное в условии задачи явление: начертить систему координат, траекторию движения, вектора скоростей и ускорений.
Записать основные уравнения кинематики равнопеременного движения в выбранной СО для произвольного момента времени:
где x0,y0 – начальное положение тела, v0x, v0y – проекции начальной скорости тела, ax, ay – проекции ускорений.
4. Записать уравнения (1)-(4) для характерных моментов времени, из которых находить требуемые в условии задачи величины, т.е. получить рабочие формулы.
Важно, чтобы учащиеся понимали, что можно получить решение любой задачи кинематики равнопеременного движения, если записаны основные уравнения (1)-(4). Важно также, чтобы они осознавали, что вид этих уравнений меняется в зависимости от выбора СО. В связи с этим, решим несколько задач, иллюстрирующих сказанное.
Задача 1. Теннисист при подаче запускает мяч с высоты h над землей. На каком расстоянии от подающего мяч ударится о землю, если начальная скорость равна v0 и направлена вверх под углом 
Решение: а). Точку отсчета (начало координат) поместим в точку на поверхности земли, где стоял теннисист в момент удара. Время начнем отсчитывать от момента удара по мячу. На рис.1 изображена система координат XOY, траектория движения мяча, вектора скорости и ускорения.
В выбранной СО начальные условия имеют вид: x0 = 0, y0 = h, ax = 0, ax = — g,
и кинематические уравнения (1)-(4) запишутся в виде:
Требуемое в условии задачи расстояние D (дальность полета) найдем из условия: D = x(tn), где время полета tn определяется из соотношения y(tn) = 0, т.е.можем записать уравнение:
При решении этого квадратного уравнения удобнее записывать его в приведенном виде x 2 + 2qx + + q = 0 и находить корни по формуле
Опыт показывает, что учащиеся зачастую не знают этого и находят корни такого уравнения по общей формуле, что осложняет выкладки. Перепишем уравнение в виде
тогда его решение
Т.к. t >= 0, то физический смысл имеет корень
Теперь из условия D =x(tn) получим рабочую формулу
б). Решим эту задачу, выбрав за точку отсчета (начало координат) точку, где находился мяч в момент удара. Время по-прежнему отсчитываем от момента удара по мячу. На рис.2 изображена система координат XOY, траектория движения мяча, вектора скорости и ускорения.
В выбранной СО начальные условия имеют вид: x0 = 0, y0 = 0, ax = 0, ax = — g,
Кинематические уравнения (1)-(4) теперь запишутся так
и время полета tn мяча до земли найдется из условия: y(tn) = — h. Дальше решение задачи повторяет способ а).
В рассмотренной задаче было безразлично, где поместить начало координат, однако в задачах, где высота, на которой происходит событие, не задана, начало координат лучше всего помещать именно в эту точку на неизвестной высоте. Направление осей выбирается из соображений удобства.
Задача 2. Тело, свободно падающее с некоторой высоты, последние h м пути прошло за время 
Решение: Начало координат поместим в точку на неизвестной высоте H, ось Y направим вертикально вниз. Время начнем отсчитывать с момента начала падения тела. На рис.3 изображена система координат и ускорение свободного падения тела.
В выбранной СО v0y = 0, y0 = 0, ay = g и уравнения кинематики (1)-(4) сведутся к двум
Т.к. в условии задачи речь идет о свободном падении тела, то в любой момент времени его координата будет равна пройденному пути. Выразим из уравнения для координаты отрезки пути H и h. Из рис.3 очевидно, что
где tn – время падения тела на землю. Получили два уравнения с двумя неизвестными H и tn. Уравнение (6) после преобразований принимает вид
Подставляя найденное tn в (5), получим искомое выражение для высоты
Таким образом, требуемые в задаче величины определены.
Следует отметить, что если на размещение начала отсчета и направление осей системы координат учащиеся еще обращают внимание, то выбор начала отсчета времени обычно ускользает из их поля зрения. Это особенно заметно при решении задач, где в движении участвует несколько тел.
Если тела начинают свое движение одновременно, то отсчет времени начинается с момента начала движения тел, а кинематические уравнения пишутся для каждого из тел.
Задача 3. Два тела, расстояние между которыми l, начинают одновременно двигаться навстречу друг другу: первое — равномерно со скоростью v, а второе – из состояния покоя равноускоренно с ускорением a. Через какое время тела встретятся?
Решение: Поместим начало координат в точку, где находилось первое тело в начальный момент, ось OX направим по движению первого тела. Отсчет времени начнем с момента начала движения тел. На рис.4 изображена ось ОХ, вектора скоростей и ускорений обоих тел.
В этой СО x10 = 0, x20 = l. Уравнение движения для первого тела
Уравнение движения для второго тела
В момент встречи x1(t) = x2(t), t – время в пути до встречи, т.е.
Задача 4. Лифт поднимается с ускорением a. В тот момент, когда его скорость стала равна v, с потолка кабины лифта начал падать болт. Высота кабины лифта h. Вычислить время падения болта.
Решение: Свяжем начало неподвижной системы координат с точкой, в которой находится пол лифта в момент, когда болт начинает падать. Время начнем отсчитывать от момента начала падения болта. На рис.5 изображена система координат (ось ОY), вектора скоростей и ускорений.
Пусть yk vk — координата и проекция скорости кабины лифта, yб vб — координата и проекция скорости болта. Для кабины лифта основные уравнения (1) — (4) запишутся в виде
а для болта примут вид
Когда болт упадет на пол, будет выполняться: yk (t) = yб (t), где t – время падения болта:
Наибольшие затруднения вызывает у учащихся выбор начала отсчета времени, и особенно запись уравнений кинематики в случае, когда тела, участвующие в движении, начинают двигаться неодновременно.
Задача 5. Тело с начальной скоростью v0 и ускорением a1 начинает двигаться из некоторой точки по прямолинейной траектории. Через время 
Решение: Начало координат свяжем с точкой, из которой начинают двигаться тела. Ось ОХ направим по движению тел. Время начнем отсчитывать от начала движения первого тела. На рис.6 изображена система координат, вектора скоростей и ускорение.
В этой СО уравнения кинематики для первого тела имеют вид
а для второго тела, с учетом того, что оно начало свое движение на 
На запись этих уравнений нужно особенно обратить внимание учащихся. В момент, когда второе тело догонит первое, будет выполняться x1(t) = x2(t), т.е.
Получаем квадратное уравнение для определения времени t
С учетом того, что t >= 0 находим
Задача 6. Два тела брошены вертикально вверх с поверхности Земли из одной точки вслед друг за другом с интервалом времени 
Решение: Начало отсчета поместим в точку бросания. Ось OY направим вертикально вверх. Отсчет времени начнем с момента бросания первого тела. На рис.7 изображена ось OY и вектора начальной скорости и ускорения свободного падения.
В выбранной СО y10 = y20 = 0, v01y = v02y = v0, a1y = a2y = -g. Уравнения кинематики для первого тела имеют вид
Основные уравнения кинематики для второго тела с учетом того, что оно начала свое движение на 
Тела “встретятся”, когда y1 (t) = y2 (t), т.е. получаем уравнение для нахождения искомого времени “встречи”
Видео:кинематика точкиСкачать

Координатный способ задания движения точки
Видео:Как решать задачи по кинематике.Скачать

Введение
Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы применим основные результаты этой теории к координатному способу задания движения материальной точки.
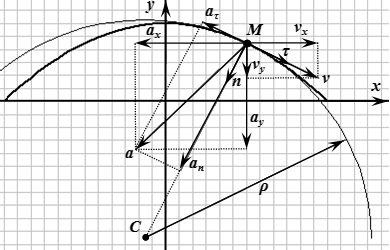
Пусть мы имеем неподвижную прямоугольную систему координат с центром в неподвижной точке . При этом положение точки M однозначно определяются ее координатами (x, y, z). Координатный способ задания движения точки – это такой способ, при котором заданы зависимости координат от времени. То есть заданы три функции от времени (при трехмерном движении):
Далее мы приводим формулы вычисления кинематических величин и пример решения задачи для координатного способа задания движения.
Видео:Задача 1.1. КИНЕМАТИКА | Учимся решать задачи по физике с нуляСкачать

Определение кинематических величин
Зная зависимости координат от времени , мы автоматически определяем радиус-вектор материальной точки M по формуле:
,
где – единичные векторы (орты) в направлении осей x, y, z .
Дифференцируя по времени , находим проекции скорости и ускорения на оси координат:
;
;
Модули скорости и ускорения:
;
.
Единичный вектор в направлении касательной к траектории:
.
Его можно определить двумя способами – по направлению скорости, или в противоположную сторону. Поэтому здесь в знаменателе стоит не модуль скорости, а алгебраическая величина скорости, которая, по абсолютной величине, равна модулю скорости, но может принимать как положительные, так и отрицательные значения: . Она является проекцией скорости на направление единичного вектора .
Алгебраическая величина тангенциального (касательного) ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории:
.
Вектор тангенциального (касательного) ускорения:
.
Здесь также, как и для скорости, – это скалярная величина, которая может принимать как положительные так и отрицательные значения: .
Нормальное ускорение:
.
Вектор нормального ускорения:
; .
Единичный вектор в направлении главной нормали траектории (то есть единичный вектор, перпендикулярный касательной и направленный к центру кривизны траектории):
.
Здесь – это модуль нормального ускорения: . Нормальное ускорение всегда направлено к центру кривизны траектории. Оно не может быть направлено в противоположную сторону.
Радиус кривизны траектории:
.
Центр кривизны траектории:
.
Единичный вектор в направлении бинормали:
.
Видео:Теоретическая механика 2020 - Практика 1. Кинематика точки.Скачать

Пример решения задачи
Определение скорости и ускорения точки по заданным уравнениям ее движения
По заданным уравнениям движения точки установить вид ее траектории и для момента времени найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Уравнения движения точки:
, см;
, см.
Решение
Определение вида траектории
Исключаем время из уравнений движения. Для этого перепишем их в виде:
; .
Применим формулу:
.
;
;
;
.
Итак, мы получили уравнение траектории:
.
Это уравнение параболы с вершиной в точке и осью симметрии .
Поскольку
, то
; или
.
Аналогичным образом получаем ограничение для координаты :
;
;
Таким образом, траекторией движения точки является дуга параболы
,
расположенная при
и .
Строим параболу по точкам.
| 0 | 6 |
| ± 3 | 5,625 |
| ± 6 | 4,5 |
| ± 9 | 2,625 |
| ± 12 | 0 |
Определяем положение точки в момент времени .
;
.
Определение скорости точки
Дифференцируя координаты и по времени , находим компоненты скорости.
.
Чтобы продифференцировать , удобно применить формулу тригонометрии:
. Тогда
;
.
Вычисляем значения компонент скорости в момент времени :
;
.
Модуль скорости:
.
Определение ускорения точки
Дифференцируя компоненты скорости и по времени , находим компоненты ускорения точки.
;
.
Вычисляем значения компонент ускорения в момент времени :
;
.
Модуль ускорения:
.
Алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории. Выберем направление совпадающим с направлением скорости . Тогда ; алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление скорости :
.
Поскольку , то вектор тангенциального ускорения направлен противоположно скорости .
Нормальное ускорение:
.
Вектор и направлен в сторону центра кривизны траектории.
Радиус кривизны траектории:
.
Траекторией движения точки является дуга параболы
; .
Скорость точки: .
Ускорение точки: ; ; .
Радиус кривизны траектории: .
Определение остальных величин
При решении задачи мы нашли:
вектор и модуль скорости:
; ;
вектор и модуль полного ускорения:
; ;
тангенциальное и нормальное ускорения:
; ;
радиус кривизны траектории: .
Определим остальные величины.
Единичный вектор в направлении касательной к траектории:
.
Вектор тангенциального ускорения:
.
Вектор нормального ускорения:
.
Единичный вектор в направлении главной нормали:
.
Координаты центра кривизны траектории:
.
Введем третью ось системы координат перпендикулярно осям и . В трехмерной системе
; .
Единичный вектор в направлении бинормали:
.
Автор: Олег Одинцов . Опубликовано: 22-02-2016 Изменено: 29-01-2020
🔥 Видео
Урок 312. Задачи по кинематике-1Скачать

5 ПРОСТЫХ ЗАДАЧ КИНЕМАТИКИ ДЛЯ НАЧИНАЮЩИХ │ФИЗИКА С НУЛЯСкачать

Лекция №1 "Кинематика материальной точки" (Булыгин В.С.)Скачать

Кинематика. Решение задач на равноускоренное движениеСкачать

Урок 7. Механическое движение. Основные определения кинематики.Скачать

Кинематика точки Задание К1Скачать

Кинематика точки. Авторы: Борисов Никита, Ларионов Егор, Петрашова Полина. Решение задачи.Скачать

Кинематика точки в плоскости. ТермехСкачать

10.1.04. Уравнение траекторииСкачать

Модуль 2. Баллистика. Равноускоренное движение в плоскости.Скачать

векторный метод решения задач по кинематикеСкачать

Как решать задачи по кинематике на ОГЭ по физике 2023?Скачать

Лекция 5.3 | Уравнение траектории | Александр Чирцов | ЛекториумСкачать

Методика решения задач по кинематике равноускоренного движенияСкачать