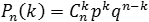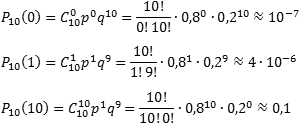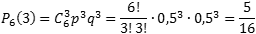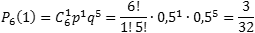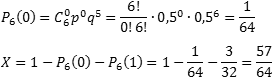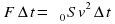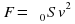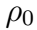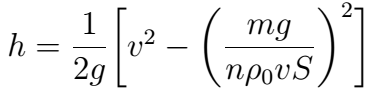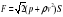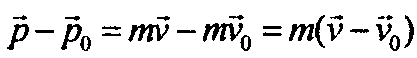Решение задач по физике на уравнение бернулли (2 видео)

Содержание

Схема Бернулли. Примеры решения задач
Задачи по гидродинамике (ЕГ)
Просмотр содержимого документа «Задачи по гидродинамике (ЕГ)»
Решение задач по физике на уравнение бернулли
📹 Видео

Видео:Закон БернуллиСкачать

Схема Бернулли. Примеры решения задач

Не будем долго размышлять о высоком — начнем сразу с определения.

— это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A , причем известна вероятность этого события P ( A ) = p. Требуется определить вероятность того, что при проведении n испытаний событие A появится ровно k раз.

Задачи, которые решаются по схеме Бернулли, чрезвычайно разнообразны: от простеньких (типа «найдите вероятность, что стрелок попадет 1 раз из 10») до весьма суровых (например, задачи на проценты или игральные карты). В реальности эта схема часто применяется для решения задач, связанных с контролем качества продукции и надежности различных механизмов, все характеристики которых должны быть известны до начала работы.

Вернемся к определению. Поскольку речь идет о независимых испытаниях, и в каждом опыте вероятность события A одинакова, возможны лишь два исхода:

A — появление события A с вероятностью p;
«не А» — событие А не появилось, что происходит с вероятностью q = 1 − p.

Важнейшее условие, без которого схема Бернулли теряет смысл — это постоянство. Сколько бы опытов мы ни проводили, нас интересует одно и то же событие A , которое возникает с одной и той же вероятностью p.

Между прочим, далеко не все задачи в теории вероятностей сводятся к постоянным условиям. Об этом вам расскажет любой грамотный репетитор по высшей математике. Даже такое нехитрое дело, как вынимание разноцветных шаров из ящика, не является опытом с постоянными условиями. Вынули очередной шар — соотношение цветов в ящике изменилось. Следовательно, изменились и вероятности.

Если же условия постоянны, можно точно определить вероятность того, что событие A произойдет ровно k раз из n возможных. Сформулируем этот факт в виде теоремы:

. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:

где C _n k — число сочетаний, q = 1 − p.

Эта формула так и называется: . Интересно заметить, что задачи, приведенные ниже, вполне решаются без использования этой формулы. Например, можно применить формулы сложения вероятностей. Однако объем вычислений будет просто нереальным.

Задача. Вероятность выпуска бракованного изделия на станке равна 0,2. Определить вероятность того, что в партии из десяти выпущенных на данном станке деталей ровно k будут без брака. Решить задачу для k = 0, 1, 10.

По условию, нас интересует событие A выпуска изделий без брака, которое случается каждый раз с вероятностью p = 1 − 0,2 = 0,8. Нужно определить вероятность того, что это событие произойдет k раз. Событию A противопоставляется событие «не A », т.е. выпуск бракованного изделия.

Таким образом, имеем: n = 10; p = 0,8; q = 0,2.

Итак, находим вероятность того, что в партии все детали бракованные ( k = 0), что только одна деталь без брака ( k = 1), и что бракованных деталей нет вообще ( k = 10):

Задача. Монету бросают 6 раз. Выпадение герба и решки равновероятно. Найти вероятность того, что:

герб выпадет три раза;
герб выпадет один раз;
герб выпадет не менее двух раз.

Итак, нас интересует событие A , когда выпадает герб. Вероятность этого события равна p = 0,5. Событию A противопоставляется событие «не A », когда выпадает решка, что случается с вероятностью q = 1 − 0,5 = 0,5. Нужно определить вероятность того, что герб выпадет k раз.

Таким образом, имеем: n = 6; p = 0,5; q = 0,5.

Определим вероятность того, что герб выпал три раза, т.е. k = 3:

Теперь определим вероятность того, что герб выпал только один раз, т.е. k = 1:

Осталось определить, с какой вероятностью герб выпадет не менее двух раз. Основная загвоздка — во фразе «не менее». Получается, что нас устроит любое k , кроме 0 и 1, т.е. надо найти значение суммы X = P ₆(2) + P ₆(3) + . + P ₆(6).

Заметим, что эта сумма также равна (1 − P ₆(0) − P ₆(1)), т.е. достаточно из всех возможных вариантов «вырезать» те, когда герб выпал 1 раз ( k = 1) или не выпал вообще ( k = 0). Поскольку P ₆(1) нам уже известно, осталось найти P ₆(0):

Задача. Вероятность того, что телевизор имеет скрытые дефекты, равна 0,2. На склад поступило 20 телевизоров. Какое событие вероятнее: что в этой партии имеется два телевизора со скрытыми дефектами или три?

Интересующее событие A — наличие скрытого дефекта. Всего телевизоров n = 20, вероятность скрытого дефекта p = 0,2. Соответственно, вероятность получить телевизор без скрытого дефекта равна q = 1 − 0,2 = 0,8.

Получаем стартовые условия для схемы Бернулли: n = 20; p = 0,2; q = 0,8.

Найдем вероятность получить два «дефектных» телевизора ( k = 2) и три ( k = 3):

Очевидно, P ₂₀(3) > P ₂₀(2), т.е. вероятность получить три телевизора со скрытыми дефектами больше вероятности получить только два таких телевизора. Причем, разница неслабая.

Небольшое замечание по поводу факториалов. Многие испытывают смутное ощущение дискомфорта, когда видят запись «0!» (читается «ноль факториал»). Так вот, 0! = 1 по определению.

P . S . А самая большая вероятность в последней задаче — это получить четыре телевизора со скрытыми дефектами. Подсчитайте сами — и убедитесь.

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Задачи по гидродинамике (ЕГ)

Задачи по гидродинамике (гидравлика). Используют уравнение Бернулли. Встречаются в задачах ЕГ дополнительного уровня

Просмотр содержимого документа
«Задачи по гидродинамике (ЕГ)»

Задачи гидродинамика. Уравнение Бернулли

1) Направленная горизонтальная струя воды бьет в вертикальную стенку. С какой силой струя давит на стенку, если скорость истечения воды v = 10 м/с и вода поступает через трубку, имеющую сечение s = 4 см2? Считать, что после удара вода стекает вдоль стенки.

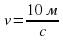
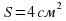
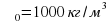
Дано F=?

Реш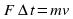

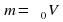
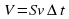
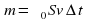
3). В сосуд, в дне которого узкое отверстие закрыт пробкой, налита вода до высоты h = 1 м. На поверхн воды находится поршень массой m = 1 кг и пло S = 100 см2. Между поршнем и стенками сосуда вода не просачивается. Найдите скорость истечения воды из отверстия в дне сосуда сразу после того, как из отверстия будет вынута пробка. Трение не учитывать.

Реш. Воспользуемся уравнением Бернулли. Давл в струе воды p0. Давл под порш на высоте h от отв p0 + mg/S. Скорость течения жидкости под поршнем м пренебречь, так как она мала по сравнению со скоростью истечения из отверстия , потому что площадь отверстия значительно меньше площади поршня. Согласно уравнению Бернулли

4) Брусок массы m удерживается в воздухе струями воды, бьющими вертикально вверх из отверстия, сечения S . Скорость воды на выходе из отверстия v. Достигнув бруска, вода разлетается от него в горизонтальной плоскости. На какой высоте над отверстием удерживается брусок? Плотность воды

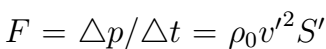
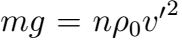
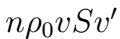
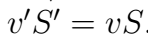
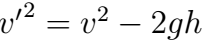
Реш Сила давления на брусок одной струи тогда

=т к из условия неразрывности струи следует, что из уравнения Бернулли имеем Решая совместно эти уравнения, получим

₁₎ Насос представляет расположенный горизонтально цилиндр с поршнем площади S и выходящим отверстием площади s, расположенном на оси цилиндра. Определить скорость истечения струи из насоса, если поршень под действ силы F перемещается с постоянной скоростью. Плотность жидкости . []

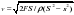
2) По наклонной плоскости стекает широкий поток воды. На расстоянии l по течению глубина потока уменьш вдвое. На каком расстоянии глубина потока уменьшится в 4 раза? [x = 5l]

_{6)по гориз}онт распол и изогнутой под прямым углом трубе сеч S течет жидкость плотности со скор V. C какой силой жидкость действует на трубу в месте изгиба если давление жидкости на выходе из трубы p? отв

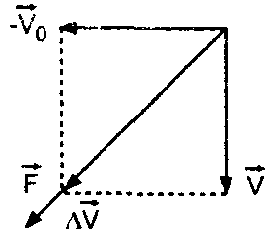
_{Реш изменение импульса в единицу времени}

откуда

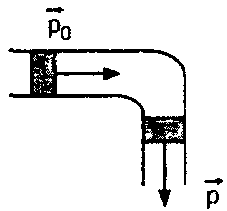
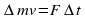
8) В широкий сосуд налита вода до высоты H. На поверхн воды налит слой масла плотности и высотой h. С какой скоростью вода начнет вытекать из сосуда, если на дне его обр отверстие? Понижением уровня воды в баке пренебречь. Плотность воды

10)В подводной лодке находящейся на глубине Н образовалась пробоина сечением S

.Какое количество воды нальется в лодку за время

Реш. Давление на одной глубине одинаково (по зну Паскаля), следовательно, снаружи давление жидкости p = ρgh. Чтобы удержать заплату, закрыв отверстие с внутренней стороны судна потребуется создать давление равное наружному p = F/S, Тогда, приравняв давления

F/S = ρgh и F = ρghS. Приняв плотность воды . имеем
F = 1,0 × 103 × 10 × 3 × 5,0 × 10−4 = 15 Н.

₇₎ Из крана выливается вода. Начиная с некоторого места, диаметр струи уменьшается на протяжении h от а до b Сколько воды вытечет из крана за время t? a=3см b=2см h=3см t=1 мин

Реш: Воспользуемся условием стационарности течения несжимаемой жидкости

Для идеальной жидкости уравнение Бернулли: .
Поскольку жид своб падает, то давл в обоих сеч одинак, и ур Бернулли прин вид: . За время t через любое сеч протекает один и тот же объем воды, поэтому . .Подставив полученное значение v₁ получим : .

2)На рис 3 2 манометра различной формы Найти разницу давлений показываемых этими манометрами если они поочередно измеряют давление в одной и той же трубе в которой течет вода со скоростью v

3)По гибкому шлангу сеч S течет жидкость плотн ρ со скор v. Найти натяж нити AB, соед концы A и B шланга, если изв, что она явл диам полуокружн, кот обр шланг (рис.).

4) Если полн открыт кран хол воды, а кран гор воды закрыт (рис.), то ванна наполн за t₁= 8 мин; если при этом на вых отв насад шланг с душем на конце, то время наполн увел до t₂ = 14 мин. Когда кран хол воды закрыт, а кран гор открыт полн, время наполн t₃ = 12 мин; при тех же усл, но с душем на конце − t₄ = 18 мин. За какое время наполн ванна, если полн отк оба крана? А если при этом насажен шланг с душем?

5) В дне бака высотой H=4см проделано отв пл 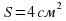Бак наполнен доверху при этом ур-нь постоянен из-за пополн из водоп. Какую подачу воды д обесп водопровод чтобы уровень в баке оставался неизменным? Коэф-т расхода от

РЕШ расход при истечении из малого отв скорость струи по ф-ле Торичелли

6)какую мощность должен иметь электродвигатель привода водяного насоса если насос при подаче создает напор H=40м а его полный кпд

Потребл мощ, т. е. мощн, кот на работу насоса затрач электродв (N_ЭД),= полезной мощн с учетом КПД: N_ЭД = N_П/η = ρgQH/η = 1000×9,81×0,05×40/0,6 = 32700 Вт = 32,7 кВт

7) Привод водян насоса обеспечивает частоту вращения его вала n₁ = 15 с -1 , при этом подача насоса Q₁ = 0,01 м 3 /с, а напор H₁ = 20 м. какова должна быть частотта вращения вала насоса, если потребуется увеличить его напор до 80 м. Как изменится при этом подача насоса?

реш: Зависимость работы парового насоса от частоты вращения вала

при увеличении частоты вращения вала насоса в 2 раза его подача тоже возрастет в 2 раза, и составит Q₂ = 0,02 м 3 /с.

Видео:Уравнение Бернулли. Практическая часть. 10 класс.Скачать

Решение задач по физике на уравнение бернулли

Уравнение Бернулли для реальной и идеальной жидкости

Уравнение Бернулли позволяет выполнить расчет водоснабжения и отопления: Подобрать диаметры и насосы. В этой статье будет расписан энергетический и геометрический смысл уравнения Бернулли.

График Бернулли и уравнение Бернулли для идеальной жидкости:

График Бернулли и уравнение Бернулли для реальной жидкости:

Смысл уравнения Бернулли

Смысл уравнения Бернули в том, чтобы показать, что внутри системы заполненной жидкостью (участка трубопровода) сохраняется общая энергия между разными точками. То есть на участке трубопровода необходимо выделить две точки, и эти две точки равны друг другу по значению полной энергии. Полная энергия состоит из потенциальной и кинетической энергии.

Назначение уравнения Бернули

Понять, как распределяется давление в системе трубопроводов. А также с помощью уравнения находить неизвестные параметры внутри системы. Например, найти давление в каждой течке пространства системы заполненной жидкостью.

Подробнее на видео: (для запуска видео кликните по окошку) На видео намного больше информации

Решая задачу с уравнением Бернулли, Вы фактически занимаетесь гидравлическим расчетом. О том, как делать гидравлический расчет — написано тут: Конструктор водяного отопления

Задача. Пример решения уравнения Бернулли

По решению задачи необходимо найти давление в точке 2 при известных параметрах: давление и расход.

Как понять уравнение Бернулли?

Для расчета уравнения Бернулли необходимо выбрать две точки в пространстве

Точка 1 – это место где известно давление

Точка 2 – это место где нужно узнать давление

Поймите, что каждый кусок формулы измеряется давлением: м.в.ст. (метр водяного столба)

То есть для того, чтобы быстро считать гидравлику систем водоснабжения и отопления, необходимо меньше всего выражаться в Барах, Паскалях и тому подобное.

Проще выражать давление в единице измерения: м.в.ст. (метр водяного столба)

Вы этим самым упростите себе жизнь… просто другая единица это еще один процесс, который отнимает время.

Сборка формулы уравнения Бернулли

Как избавится от минуса?

Как избавится от множителя (-1)?

Необходимо множитель (-1) помножить на каждый слагаемый член. Знак каждого слагаемого члена меняется на противоположный. То есть (+ на -) (- на +). Далее перестановка слагаемых.

Что такое идеальная жидкость?

Идеальная жидкость — это жидкость, не обладающая внутренним трением. То есть такая жидкость не создает гидравлическое сопротивление.

Реальная жидкость — это жидкость, которая обладает вязкостью. То есть внутренним сопротивлением.

Формула Бернулли для реальной жидкости

Коэффициент Кориолиса – это поправка кинетической энергии на реальную жидкость.

Потому что реальная жидкость движется не равномерно

У реальной жидкости серединная струйка воды движется быстрее остальных. При ламинарном режиме градиент: Чем ближе к стенке, тем медленнее движется поток воды.

Формула коэффициента Кориолиса

Что такое коэффициент Кориолиса?

Коэффициент Кориолиса характеризует отношение действительной кинетической энергии потока жидкости в данном сечении к той кинетической энергии потока, которую он имел бы, если бы все частицы двигались с одинаковой скоростью, равной средней скорости потока.

Чему равен коэффициент Кориолиса?