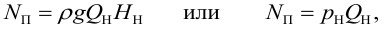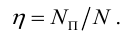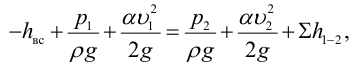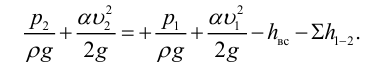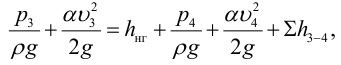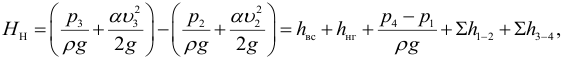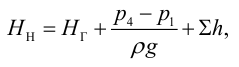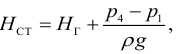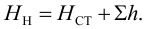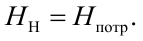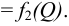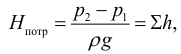ЗАДАНИЯ
К выполнению расчетно – графической работы
По дисциплине «Гидравлика»
Тема: гидростатика
Северодвинск
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Гидравлика, или техническая механика жидкостей— это наука о законах равновесия и движения жидкостей, о способах применения этих законов к решению практических задач;
Жидкостью называют вещество, находящееся в таком агрегатном состоянии, которое сочетает в себе черты твердого состояния (весьма малая сжимаемость) и газообразного (текучесть). Законы равновесия и движения капельных жидкостей в известных пределах можно применять и к газам.
На жидкость могут действовать силы, распределенные по ее массе (объему), называемые массовыми, и по поверхности, называемые поверхностными. К первым относятся силы тяжести и инерции, ко вторым — силы давления и трения.
Давлением называется отношение силы, нормальной к поверхности, к площади. При равномерном распределении
Касательным напряжением называется отношение силы трения, касательной к поверхности, к площади:
Если давление р отсчитывают от абсолютного нуля, то его называют абсолютным (рабс), а если от условного нуля (т. е. сравнивают с атмосферным давлением ра, то избыточным (ризб):
Если Рабс 3 ), определяемая для однородной жидкости отношением ее массы m к объему V:
Плотность пресной воды при температуре Т = 4°С ρ = = 1000 кг/м 3 . В гидравлике часто пользуются также понятием удельного веса γ (Н/м 3 ), т.е весом G единицы объема жидкости:
Плотность и удельный вес связаны между собой соотношением:
где g — ускорение свободного падения.
Для пресной воды γвод= 9810 Н/м 3
Важнейшие физические параметры жидкостей, которые используются в гидравлических расчетах,— сжимаемость, температурное расширение, вязкость и испаряемость.
Сжимаемость жидкостей характеризуется модулем объемной упругости К, входящим в обобщенный закон Гука:
где ΔV— приращение (в данном случае уменьшение) объема жидкости V, обусловленное увеличением давления на Δр. Например, для воды Квод ≈2 . 10 3 МПа.
Температурное расширение определяется соответствующим коэффициентом, равным относительному изменению объема, при изменении температуры на 1 °С:
Вязкость — это способность жидкости сопротивляться сдвигу. Различают динамическую (μ) и кинематическую (ν) вязкости. Первая входит в закон жидкостного трения Ньютона, выражающий касательное напряжение τ через поперечный градиент скорости dv/dt:
Кинематическая вязкость связана с динамической соотношением
Единицей кинематической вязкости является м 2 /с.
Испаряемость жидкостей характеризуется давлением насыщенных паров в функции температуры.
Давлением насыщенных паров можно считать то абсолютное давление, при котором жидкость закипает при данной температуре. Следовательно, минимальное абсолютное давление, при котором вещество находится в жидком состоянии, равно давлению насыщенных паров рн.п.
Основные параметры некоторых жидкостей, их единицы в СИ и внесистемные единицы, временно допускаемые к применению, приведены в Приложениях 1. 3.
ГИДРОСТАТИКА
Давление в неподвижной жидкости называется гидростатическим и обладает следующими двумя свойствами:
— на внешней поверхности жидкости оно всегда направлено во нормали внутрь объема жидкости;
— в любой точке внутри жидкости оно по всем направлениям одинаково, т. е. не зависит от угла наклона площадки, по которой действует.
Уравнение, выражающее гидростатическое давление р в любой точке неподвижной жидкости в том случае, когда из числа массовых сил на нее действует лишь одна сила тяжести, называется основным уравнением гидростатики:
где p0 — давление на какой-либо поверхности уровня жидкости, например на свободной поверхности; h — глубина расположения рассматриваемой точки, отсчитанная от поверхности с давлением р0.
В тех случаях, когда рассматриваемая точка расположена выше поверхности с давлением р0, второй член в формуле (1.1) отрицателен.
Другая форма записи того же уравнения (1.1) имеет вид
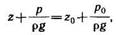
где z и z0 — вертикальные координаты произвольной точки и свободной поверхности, отсчитываемые от горизонтальной плоскости вверх; p/(pg) — пьезометрическая высота.
Гидростатическое давление может быть условно выражено высотой столба жидкости p/ρg.
В гидротехнической практике внешнее давление часто равноатмосферному: P0=Рат
Величина давления Pат = 1 кГ/см 2 = 9,81 . 10 4 н/м г называетсятехнической атмосферой.
Давление, равное одной технической атмосфере, эквивалентно давлению столба воды высотой 10 метров, т. е.
Гидростатическое давление, определяемое по уравнению (1.1), именуется полным или абсолютным давлением. В дальнейшем будем обозначать это давление рабс или p’. Обычно в гидротехнических расчетах интересуются не полным давлением, а разницей между полным давлением в атмосферным, т. е. так называемым манометрическим давлением
В дальнейшем изложении сохраним обозначение р за манометрическим давлением.
Сумма членов 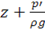
Сумма 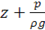
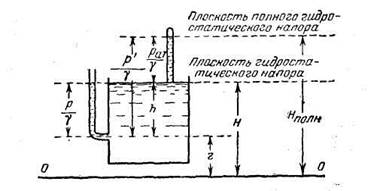
На рис. 1.1 плоскость полного гидростатического напора и плоскость гидростатического напора показаны для случая, когда свободная поверхность находится под атмосферным давлением р0=pат.
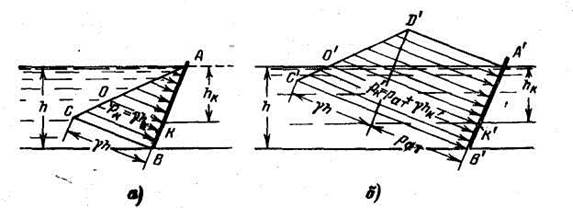
Графическое изображение величины и направления гидростатического давления, действующего на любую точку поверхности, носит название эпюры гидростатического давления. Для построения эпюры нужно отложить величину гидростатического давления для рассматриваемой точки нормально к поверхности, яа которую оно действует. Так, например, эпюра манометрического давления на плоский наклонный щит АВ (рис. 1.2,а) будет представлять треугольник ABC, а эпюра полного гидростатического давления — трапецию A’B’C’D’ (рис. 1.2,б).
Каждый отрезок эпюры на рис. 1.2,а (например О К) будет изображать манометрическое давление в точке К, т. е. pK = ρghK, а на рис. 1.2,б — полное гидростатическое давление
Сила давления жидкости на плоскую стенку равна произведению гидростатического давления ρс в центре тяжести площади стенки на площадь стенки S, т. е.
Центр давления (точка приложения силы F) расположен ниже центра тяжести площади или совпадает с последним в случае горизонтальной стенки.
Расстояние между центром тяжести площади и центром давления в направлении нормали к линии пересечения плоскости стенки со свободной поверхностью жидкости равно
где J0 — момент инерции площади стенки относительно оси, проходящей через центр тяжести площади и параллельной линии пересечения плоскости стенки со свободной поверхностью: ус — координата центра тяжести площади.
Сила давления жидкости на криволинейную стенку, симметричную относительно вертикальной плоскости, складывается из горизонтальной FГ и вертикальной FB составляющих:
Горизонтальная составляющая FГ равна силе давления жидкости на вертикальную проекцию данной стенки:
Вертикальная составляющая FB равна весу жидкости в объеме V, заключенном между данной стенкой, свободной поверхностью жидкости и вертикальной проекцирующей поверхностью, проведенной по контуру стенки.
Если избыточное давление р0 на свободной поверхности жидкости отлично от нуля, то при расчете следует эту поверхность мысленно поднять (или опустить) на высоту (пьезометрическую высоту) p0/(ρg)
Плавание тел и их остойчивость.Условие плавания тела выражается равенством
где G — вес тела;
Р — результирующая сила давления жидкости на погруженное в нее тело — архимедова сила.
Сила Р может быть найдена по формуле
где ρg — удельный вес жидкости;
W — объем жидкости, вытесненной телом, или водоизмещение.
Сила Р направлена вверх и проходит через центр тяжести водоизмещения.
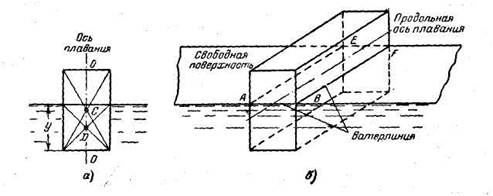
Осадкой тела у называется глубина погружения наинизшей точки смоченной поверхности (рис. 1.3,а). Под осью плавания понимают линию, проходящую через центр тяжести С и центр водоизмещения D, соответствующий/ нормальному положению тела в состоянии равновесия (рис. 1.3, а)-
Ватерлинией называется линия пересечения поверхности плавающего тела со свободной поверхностью жидкости (рис. 1.3,б). Плоскостью плавания ABEF называется плоскость, полученная от пересечения тела свободной поверхностью жидкости, или, иначе плоскость, ограниченная ватерлинией.
Кроме выполнения условий плавания (1.5) тело (судно, баржа и т.д.) должно удовлетворять условиям остойчивости. Плавающее тело будет остойчивым в том случае, если при крене сила веса G и архимедова сила Р создают момент, стремящийся уничтожить крен и вернуть тело в исходное положение.
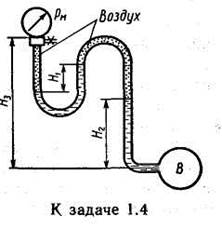
При надводном плавании тела (рис. 1.4) центр водоизмещения при малых углах крена (α δ (1.7)
где ρ — метацентрический радиус, т. е. расстояние между центром водоизмещения и метацентром
δ — расстояние между центром тяжести тела С и центром водоизмещения D. Метацентрический радиус ρ находится по формуле:

где J0 — момент инерции плоскости плавания или площади, ограниченной ватерлинией, относительно продольной оси (рис. 1-8,6);
Если центр тяжести тела С расположен выше центра водоизмещения и метацентра, то тело неостойчиво; возникающая пара сил G и Р стремится увеличить крен (рис. 1.4,в).
УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ
При решении задач по гидростатике прежде всего нужно хорошо усвоить и не смешивать такие понятия, как давление р и сила F.
При решении задач на определение давления в той или иной точке неподвижной жидкости следует пользоваться основным уравнением гидростатики (1.1). Применяя это уравнение, нужно иметь в виду, что второй член в правой части этого уравнения может быть как положительным, так и отрицательным. Очевидно, что при увеличении глубины давление возрастает, а при подъеме — уменьшается.
Необходимо твердо различать давления абсолютное, избыточное и вакуум и обязательно знать связь между давлением, удельным весом и высотой, соответствующей этому давлению (пьезометрической высотой).
При решении задач, в которых даны поршни или системы поршней, следует писать уравнение равновесия, т. е. равенство нулю суммы всех сил, действующих на поршень (систему поршней).
Решение задач следует проводить в международной системе единиц измерения СИ.
Решение задачи должно сопровождаться необходимыми пояснениями, рисунками (принеобходимости), перечислением исходных величин (графа «дано»), переводом единиц в систему СИ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ГИДРОСТАТИКЕ
Задача 1. Определить полное гидростатическое давление на дно сосуда, наполненного водой. Сосуд сверху открыт, давление на свободной поверхности атмосферное. Глубина воды в сосуде h = 0,60 м.
В данном случае имеем р0=рат и потому применим формулу (1.1) в виде
р’=9,81.10 4 +9810 . 0,6 = 103986 Па
Ответ р’=103986 Па
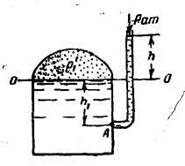
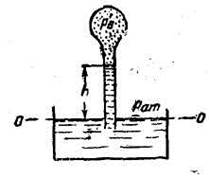
Составим условия равновесия для общей точки А (см. рисунок).Давление в точке А слева:
Приравнивая правые части уравнений, и сокращая на γg получаем:
Указанное уравнение можно также получить, составив условие равновесия для точек, расположенных в любой горизонтальной плоскости, например в плоскости ОО (см. рисунок). Примем за начало шкалы отсчета пьезометра плоскость ОО и из полученного уравнения найдем высоту столба воды в пьезометре h.

Пьезометр измеряет величину манометрического давления, выраженного высотой столба жидкости.
Ответ: h = 0,6 метра
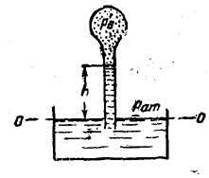
Составим условие равновесия относительно горизонтальной плоскости О-О:
гидростатическое давление, действующее изнутри:
Гидростатическое давление в плоскости О—О, действующее с внешней стороны,
Так как система находится в равновесии, то
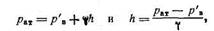 |
т. е. вакуумметр измеряет недостаток давления до атмосферного или вакуум, выраженный высотой столба жидкости.
Высота, на которую поднимается жидкость, при γ=9810 Н/м 3
Ответ: h = 0,5 метра
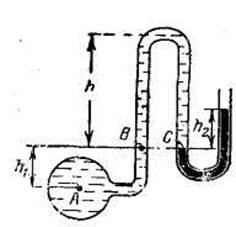
Решение: Находим давление в точке В: р’В=р’А-γh1, так как точка В расположена выше точки А на величину h1. В точке С давление будет такое же, как в точке В, так как давление столба воды h взаимно уравновешивается, т. е.
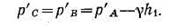 |
Определим давление в точке С справа с учетом атмосферного давления, т. е.
Приравнивая оба уравнения, получаем:
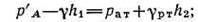 |
отсюда манометрическое давление:
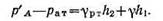 |
Подставляя числовые значения, получаем:
ЗАДАЧИ
Задача 1.1. Канистра, заполненная бензином и не содержащая воздуха, нагрелась на солнце до температуры 50 °С. На сколько повысилось бы давление бензина внутри канистры, если бы она была абсолютно жесткой? Начальная температура бензина 20 0 С. Модуль объемной упругости бензина принять равным K=1300 МПа, коэффициент температурного расширения β = 8 . 10 -4 1/град.
Задача 1.2. Определить избыточное давление на дне океана, глубина которого h=10 км, приняв плотность морской воды ρ=1030 кг/м 3 и считая ее несжимаемой. Определить плотность воды на той же глубине с учетом сжимаемости и приняв модуль объемной упругости K = 2 . 10 3 МПа.
Задача 1.3. Найти закон изменения давления р атмосферного воздуха по высоте z, считая зависимость его плотности от давления изотермической. В действительности до высоты z=11 км температура воздуха падает по линейному закону, т. е. T=T0-βz, где β = 6,5 град/км. Определить зависимость p = f(z) с учетом действительного изменения температуры воздуха с высотой.
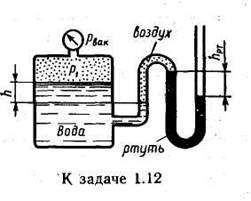
Задача 1.4. Определить избыточное давление воды в трубе В, если показание манометра рм = 0,025 МПа. Соединительная трубка заполнена водой и воздухом, как показано на схеме, причем Н1 = 0,5 м; Н2=3 м.
Как изменится показание манометра, если при том же давлении в трубе всю соединительную трубку заполнить водой (воздух выпустить через кран К)? Высота Н3 = 5 м.
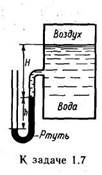
Задача 1.7. Определить абсолютное давление воздуха всосуде, если показание ртутного прибора h = 368 мм, высота H=1 м. Плотность ртути ρ= 13600 кг/м 3 . Атмосферное давление 736 мм рт. ст.
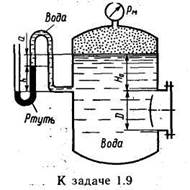
1) показание манометра рм = 0,08 МПа; H0=1,5 м;
2) показание ртутного вакуумметра h = 73,5 мм при а= 1м; ρрт= 13600 кг/м 3 ; Н0=1,5 м.
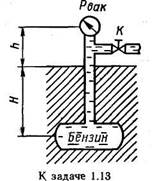
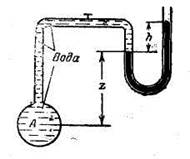
Задача 1.13. При перекрытом кране трубопровода К определить абсолютное давление в резервуаре, зарытом на глубине Н=5 м, если показание вакуумметра, установленного на высоте h=1,7 м, равно рвак = 0,02 МПа. Атмосферное давление соответствует ра = 740 мм рт. ст. Плотность бензина ρб = 700 кг/м 3 .
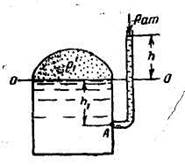
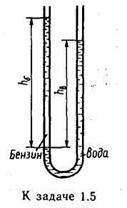
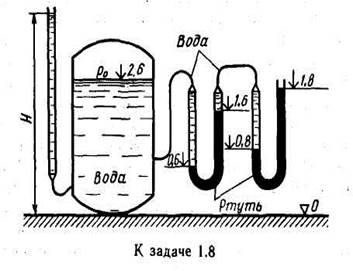
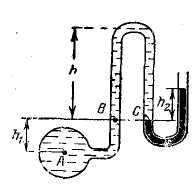
Задача 1.15.Определить вакуум рвак и абсолютное давление внутри баллона р’в (рис. 1-11), если показание вакуумметра h =0,7 м вод. ст.
1) в баллоне и в левой трубке — вода, а в правой трубке — ртуть (ρ=13600 кг/м 3 );
2) в баллоне и левой трубке — воздух , а в правой трубке — вода.
Определить, какой процент составляет давление столба воздуха в трубке от вычисленного во втором случае манометрического давления?
При решении задачи принять h1 = 70 см,h 2= = 50 см.
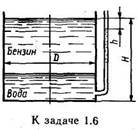
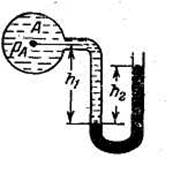
Задача 1.17. Чему будет равна высота ртутного столба h2 (рис. к задаче 1.16), если манометрическое давление нефти в баллоне А pа = 0,5 ат, а высота столба нефти (ρ=800 кг/м 3 ) h1=55 см?
Задача 1.21.Кусок гранита весит в воздухе 14,72 Н и 10,01 Н в жидкости, имеющей относительный удельный вес 0,8. Определить объем куска гранита, его плотность и удельный вес.
Задача 1.22 Деревянный брус размером 5,0 х 0,30 м и высотой 0,30м спущен в воду. На какую глубину он погрузится, если относительный вес бруса 0,7? Определить, сколько человек могут встать на брус, чтобы верхняя поверхность бруса оказалась бы заподлицо со свободной поверхностью воды, считая, что каждый человек в среднем имеет массу 67,5 кг.
Задача 1.23 Прямоугольная металлическая баржа длиной 60 м, шириной 8 м, высотой 3,5 м, загруженная песком, весит 14126 кН. Определить осадку баржи. Какой объем песка Vп нужно выгрузить, чтобы глубина погружения баржи была 1,2 м, если относительный удельный вес влажного песка равен 2,0?
Задача 1.24. Объемное водоизмещение подводной лодки 600 м 3 . С целью погружения лодки отсеки были заполнены морской водой в количестве 80 м 3 . Относительный удельный вес морской воды 1,025. Определить: какая часть объема лодки (в процентах) будет погружена в воду, если из подводной лодки удалить всю воду и она всплывет; чему равен вес подводной лодки без воды?
- Основы гидравлики
- Решение задач по гидравлике
- Решение задач с использованием закона Архимеда
- Решение задач с применением основного уравнения гидростатики
- Гидравлика задачи с решением
- Гидравлика
- Основные физические свойства жидкостей и газов
- Задача №1.2
- Гидростатика
- Указания к решению задач:
- Задача №2.1
- Применение уравнения Бернулли
- Задача №3.1
- Гидравлические сопротивления
- Задача №4.1
- Задачи на гидравлический расчет трубопроводов
- Задача на гидравлический расчет сложного напорного трубопровода
- Задача на расчет трубопровода с насосной подачей жидкости
- 🎬 Видео
Видео:Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Основы гидравлики
Видео:Видеолекция «Решение задач на Основное уравнение гидростатики»Скачать

Решение задач по гидравлике
Решение задач с использованием закона Архимеда
Задача
Баркас массой mб = 250 кг изготовлен в форме параллелепипеда шириной b = 1 м, длиной l = 3 м, высота бортов h = 0,3 м.
Определить, сколько человек могут разместиться в баркасе, не потопив его.
Средняя масса человека mч = 70 кг, плотность воды ρ = 1000 кг/м 3 .
Определим водоизмещение баркаса Мmax , которое равно массе воды, вытесненной им при полном погружении (по обрез бортов).
Для этого определим объем корпуса баркаса и умножим полученный результат на плотность воды:
Мmax = b×l×h×ρ = 1×3×0,3×1000 = 900 кг.
Чтобы найти грузоподъемность Мгр баркаса, необходимо из полученного результата вычесть массу самого баркаса:
Разделив полученную максимальную грузоподъемность на среднюю массу человека, и округлив результат до целого числа, получим допустимое количество пассажиров баркаса:
Ответ: баркас может принять на борт не более 9 человек.
Задача
Медный шар диаметром d = 100 мм весит в воздухе G1 = 45,7 Н, а при погружении в жидкость его вес стал равен G2 = 40,6 Н.
Определить плотность жидкости.
Вес шара в жидкости меньше, чем его вес в воздухе, поскольку в жидкости на него действует выталкивающая архимедова сила, равная весу вытесненной шаром жидкости.
Очевидно, что вес вытесненной шаром жидкости будет равен разности между весом шара в воздухе и его весом в жидкости:
Чтобы определить плотность жидкости, необходимо ее массу разделить на объем, который равен объему шара, определяемого по формуле:
Vш = πd 3 /6 = 3,14×0,1 3 /6 = 0,00052 м 3 .
Массу жидкости можно определить, зная ее вес:
Определив массу и объем, находим плотность жидкости:
ρ = mж/Vш = 0,52/0,00052 = 1000 кг/м 3 .
Ответ: плотность жидкости равна 1000 кг/м 3 (судя по плотности, жидкость — вода).
Задача
Баржу, имеющую форму параллелепипеда, загрузили песком в количестве 18 тонн. Ее осадка (глубина погружения) составила h0 = 0,5 м.
Определить массу пустой баржи, если ее размеры: длина l = 12 м; ширина b = 4 м.
Какова полная грузоподъемность баржи, если высота ее бортов h = 1 м.
Плотность воды принять равной 1000 кг/м 3 .
В соответствии с законом Архимеда, на баржу со стороны воды действует выталкивающая сила, равная весу воды, вытесненной погруженной частью баржи. Этот вес (обозначим его GВ ) можно определить, зная ширину, длину и осадку баржи, а также плотность воды:
GВ = mg = b×l×h0×ρ×g = 4×12×0,5×1000×9,81 = 235400 Н.
Итак, на баржу действует выталкивающая сила, равная 235400 Н, удерживая ее в равновесном состоянии на поверхности воды. Следовательно, вес GБГ баржи с грузом тоже равен 235400 Н, тогда масса баржи с грузом равна:
mБГ = GБГ/g = 235400/9,81 ≈ 24000 кг.
Чтобы найти массу пустой баржи, необходимо из массы груженой баржи вычесть массу груза:
Очевидно, что при полном погружении баржи в воду (по самые борта), выталкивающая архимедова сила увеличится в два раза по сравнению с рассмотренным нами случаем, т. е. составит 2×235400 = 470800 Н.
Данная сила характеризует водоизмещение баржи, т. е. максимальное количество вытесняемой ее корпусом воды.
Однако, эта величина не характеризует полную грузоподъемность баржи, поскльку она сама имеет вес.
Исходя из этого, полная грузоподъемность баржи может быть подсчитана, как разница между массой вытесненной баржой воды и массой баржи:
Мmax = mВ — mБ = 47080 – 6000 = 41080 кг.
Ответ: пустая баржа весит 6 тонн, а ее полная грузоподъемность — 41 тонна.
Задача
Для переправы грузов через реку построен плот из 25 штук пустых железных бочек.
Размеры бочек: диаметр d = 0,8 м, высота h = 1,3 м.
Масса одной бочки m = 50 кг.
Определить грузоподъемность плота Мmax при условии его полного погружения.
Плотность воды принять равной ρ = 1000 кг/м 3 .
Определим объем бочек, из которых изготовлен плот:
V = 25 h πd 2 /4 = 25×1,3×3,14×0,8 2 /4 = 16,33 м 3 .
Масса этих бочек: mБ = 25m = 25 × 50 = 1250 кг.
Масса воды, вытесняемой бочками при полном погружении плота, равна произведению плотности воды на объем бочек:
Грузоподъемность плота равна массе вытесняемой бочками воды с учетом массы самих бочек:
Мmax = mВ – mБ = 16330 – 1250 = 15080 кг.
Ответ: максимальная грузоподъемность плота равна 15080 кг.
Решение задач с применением основного уравнения гидростатики
Задача
На рисунке изображены три сосуда разной формы, в каждый из которых налита вода на одинаковую высоту Н .
Площадь свободной поверхности в сосуде а больше площади свободной поверхности в сосуде в в два раза, но в два раза меньше площади свободной поверхности в сосуде б .

Во сколько раз сила давления на дно в сосуде а будет отличаться от силы давления на дно в сосуде в ?
Ответ обоснуйте основным уравнением гидростатики.
В соответствии с основным уравнением гидростатики p = p0 + γ(z0 – z) , т. е. давление в любой точке объема жидкости зависит от внешнего давления p0 и глубины погружения рассматриваемой точки.
Поскольку внешнее давление для всех трех сосудов равно атмосферному давлению, т. е. одинаково, то давление на каждую из точек поверхности дна зависит только от уровня Н (т. е. глубины, равной z0 — z ). Очевидно, что для всех трех сосудов, уровень жидкости в которых одинаков, давление на дно тоже будет одинаково.
Тогда и сила давления на дно, определяемая, как произведение площади дна на величину давления, во всех трех сосудах будет одинакова, несмотря на то, что они имеют разную форму.
Задача
Определить избыточное давление в забое скважины глубиной h = 85 м, которая заполнена глинистым раствором плотностью ρ = 1250 кг/м 3 .
Избыточное давление – это давление, которое оказывает столб жидкости на единицу площади на данной глубине без учета внешнего давления (атмосферы) на поверхности жидкости, и определяется, как произведение удельной плотности жидкости на высоту столба (глубины погружения).
Удельная плотность жидкости определяется, как произведение абсолютной плотности на ускорение свободного падения.
Тогда избыточное давление в скважине исходя из условий задачи можно записать так:
pизб = γh = ρgh = 1250×9,81×85 = 1040000 Па ≈ 1 МПа.
Ответ: избыточное давление в забое скважины составляет примерно 1 МПа.
Задача
Водолазы при подъеме затонувшего судна работали в море на глубине h = 50 м.
Определите давление воды на этой глубине и силу давления на скафандр водолаза, если площадь поверхности S скафандра равна 2,5 м 2 .

Давление воды на глубине 50 м складывается из атмосферного давления p0 и избыточного давления, обусловленного столбом воды высотой 50 м:
p = p0 + ρgh = 1,013×10 5 + 1000×9,81×50 = 5,918×10 5 Па.
Сила давления воды на скафандр водолаза равна произведению площади скафандра на избыточное давление (внутри скафандра давление равно атмосферному, поэтому p0 не учитывается) и определяется по формуле:
F = ρgh×S = 1000×9,81×50×2,5 = 1226250 Н ≈ 1226 кН.
Ответ: давление воды на глубине 50 м равно 591 МПа, а сила давления на скафандр равна 1226 кН.
Задача
После сжатия воды в цилиндре под поршнем давление в ней увеличилось на 3 кПа.
Необходимо определить конечный объем V2 воды в цилиндре, если ее первоначальный объем составлял V1 = 2,55 л.
Коэффициент объемного сжатия воды βV = 4,75 • 10 -10 Па -1 .
Приведем исходные данные задачи к системе единиц СИ: V1 = 2,55л = 2,25х10 -3 м 3 , Δp = 3 кПа = 3000 Па.
Тогда конечный объем воды в цилиндре будет равен сумме первоначального объема V1 и уменьшения объема ΔV в результате сжатия:
V2 = V1 + ΔV = (2,25×10 -3 ) + (2,25×10 -3 ×3000×4,75×10 -10 ) = 2,25000320625×10 -3 м 3 = 2,2500032625 л.
Ответ: конечный объем воды 2,2500032625 л, т. е. изменился ничтожно мало.
Скачать задачи по гидравлике с вариантами решений
(в формате Word, размер файла 324 кБ — 27 задач с решениями и вопросы по насосам)
Видео:Основное уравнение гидростатики (задачи)Скачать

Гидравлика задачи с решением
Видео:Основной закон гидростатикиСкачать

Гидравлика
Гидравлика — это наука, изучающая законы равновесия и движения жидкостей и газов, в том числе паров жидкости, то есть воды. Если строго следовать научно-техническим канонам, то гидравлика, в отличие от теоретической гидромеханики, управляет сложным и строгим математическим аппаратом («Механика жидкостей и газов»), прежде всего, является технической наукой, главной задачей которой является решение проблем на практике. По этой причине разработка практических методов расчета в гидравлике очень часто предполагает использование различных предположений и допущений, во многих случаях ограничиваясь одномерными потоками в стационарных режимах. Во многих случаях используются результаты экспериментальных данных, которые после соответствующей математической обработки используются в качестве математических уравнений для решения целого ряда аналогичных задач.
Основные физические свойства жидкостей и газов
Указания к решению задач:
Основными физическими характеристиками жидкости являются плотность, вязкость, сжимаемость, температурное расширение, испаряемость. Характеристики определяются с помощью следующих формул:
динамическая вязкость 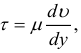
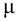
сжимаемость 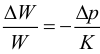
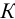
определяется соответствующим коэффициентом, равным относительному изменению объема, при изменении температуры на 1 °С;
испаряемость Жидкости испаряются при любой температуре при наличии свободного объема. Испарение происходит с поверхности, причем тех молекул, которые имеют повышенную в 5-10 раз энергию по сравнению со средней. С повышением внешнего давления температура кипения увеличивается, а с понижением (вакуум) — уменьшается. Зависимость давления насыщенного пара от температуры выражается уравнением Клаузиуса-Клапейрона
где 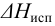
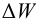
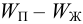
При испарении жидкости резко изменяется объем паровой фазы по сравнению с жидкой, поэтому объемом жидкости в уравнении можно пренебречь, тогда
С учетом уравнения Менделеева-Клапейрона
Интегрировав данное выражение получим формулу Клазиуса-Клапейрона
Возможно эта страница вам будет полезна:
Задача №1.2
Определить плотности воды и нефти при 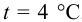
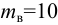
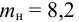
Решение:
плотность воды при заданных условиях:
а плотность нефти:
Видео:Решение задачи по гидравлике (механике жидкости) - давление в точкеСкачать

Гидростатика
Гидростатика — это раздел физики непрерывных сред, изучающий равновесие жидкостей, особенно в области гравитации.
Гидростатика — это теория поведения неподвижных жидкостей. Прежде всего, полезно сравнить гидростатику с теорией упругости, в которой изучается равновесие твердых тел.
Указания к решению задач:
Гидростатика — это раздел гидравлики, изучающий покоящиеся жидкости. Она изучает законы равновесия жидкости и распределение в ней давления. Основные величины, используемые в гидростатике -это давление 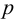
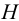
Гидростатическим давлением 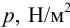
Гидростатическое давление жидкости складывается из давления на ее свободную поверхность 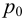
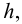
где 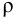
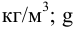
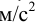
Гидростатическое давление называют абсолютным 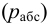
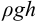
где 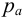
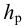
Вакуумметрическое давление, или вакуум, — недостаток давления до атмосферного, т.е. разность между атмосферным или барометрическим и абсолютным давлением:
Полная сила, действующая на плоскую стенку 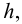
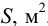
где 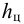
Полная сила, действующая на цилиндрическую поверхность:
где 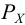
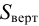
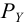
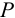
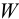
Направление полной силы давления 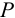
На любое тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости, вытесненной телом (закон Архимеда):
где 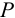
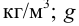
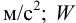
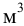
Возможно эта страница вам будет полезна:
Задача №2.1
Определить полное гидростатическое и манометрическое давление на дне сосуда, наполненного водой. Сосуд сверху открыт, давление на свободной поверхности атмосферное. Глубина воды в сосуде 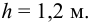
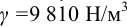
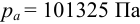
Решение:
1) Определим полное гидростатическое давление в точке:
2) Манометрическое давление на дне сосуда определяется как разность между полным гидростатическим и атмосферным давлениями:
Применение уравнения Бернулли
Основным объектом изучения гидродинамики является поток жидкости. Различают объемный расход 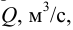
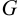
где 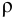
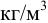
Скорость потока определяется как объемный расход вещества через единицу площади сечения потока, 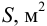
Отсюда следует, что скорости обратно пропорциональны площадям поперечного сечения потоков:
При установившемся движении через любое поперечное сечение потока в единицу времени проходит одно и то же количество жидкости (уравнение неразрывности потока):
Основным уравнением гидравлики, определяющим связь между давлением и скоростью в движущемся потоке идеальной жидкости, является уравнение Берну или, все члены которого имеют размерность длины и измеряются высотой столба жидкости:
где 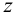
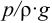
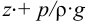
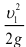
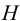
Физически уравнение Бернулли есть математическая запись закона сохранения и превращения энергии применительно к движущейся жидкости. Из уравнения следует, что если на участке потока уменьшается скорость (кинетическая энергия), то на этом участке должно возрастать давление (потенциальная энергия).
Если энергию жидкости отнести к единице ее объема, то члены уравнения Бернулли будут иметь размерность давления, а само уравнение примет вид, которым также часто пользуются:
Если же энергию жидкости отнести к единице массы, можно получить 3-ю формулу записи уравнения:
Для потока реальной (вязкой) жидкости уравнение Бернулли запишем в следующем виде:
где 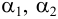
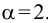
Указания к решению задач:
Часть задач раздела рассчитана на применение уравнения Бернулли для идеальной жидкости, без учета гидравлических потерь. Другая часть задач решается с помощью уравнений Бернулли для потока реальной жидкости.
При применении уравнения Бернулли важно правильно выбрать два сечения, для которых оно записывается.
В качестве сечений рекомендуется выбирать:
- свободную поверхность жидкости в резервуаре
);
- выход в атмосферу
;
- сечение, где установлен манометр, пьезометр или вакуумметр;
- неподвижный воздух на достаточном удалении от трубы всасывания из атмосферы.
Уравнение Бернулли рекомендуется вначале записывать в общем виде, а затем произвести замену его членов заданными параметрами. Члены уравнения Бернулли записываются по потоку жидкости, геометрическая высота 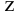
В случае подвода жидкости к резервуару, считается, что теряется вся кинетическая энергия жидкости. Коэффициент Кориолиса « учитывается в случае ламинарного режима.
Возможно эта страница вам будет полезна:
Задача №3.1
Определить расход в водопроводной трубе, если средняя скорость 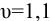
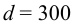
Решение:
Гидравлические сопротивления
Указания к решению задач:
Общие потери напора условно считают равными сумме потерь напора, вызываемых каждым сопротивлением:
где 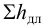
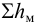
Местные потери определяются по формуле Вейсбаха:
где 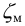
Числовое значение 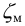
Иногда на него влияет число Рейнольдса. Которое для труб диаметром 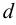
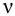
При значениях 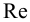
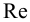
При турбулентном режиме, в случае внезапного расширения потери напора определяются формулой Борда:
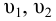
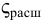
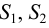
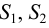
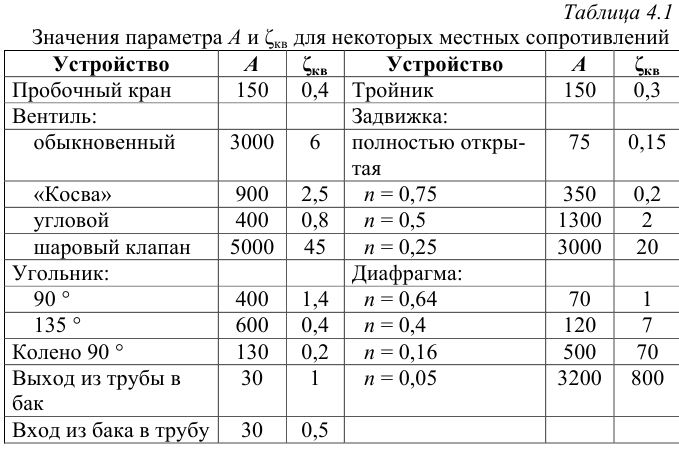
Для других местных сопротивлений коэффициенты находят в справочниках.
Для определения потерь давления на местных сопротивлениях выражение (4.2) приобретает вид:
Потери напора на трение по длине 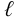
где 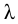
Потери давления на трение по длине находят по следующей формуле
При ламинарном течении
При турбулентном режиме, если
для переходных труб, по формуле Альштуля,
коэффициент 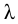
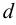

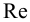
Для гладких труб, по формуле Блазиуса, если
Для гладких труб, по формуле Никурадзе, если
Для области шероховатых труб, по формуле Шифринсона, если
Местные потери в трубах при малых числах Рейнольдса зависят не только от геометрических характеристик сопротивления [1], но и от числа Рейнольдса и могут быть при ориентировочных расчетах найдены по формуле Альтшуля:
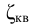
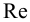
Возможно эта страница вам будет полезна:
Задача №4.1
Применяемые в водоснабжении и канализации трубы имеют минимальный диаметр 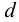
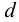
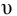
Решение:
Температура воды в системах водоснабжения и канализации изменяется в пределах от 0 °С до 30 °С, кинематические вязкости по таблицам [1] составляют
1) Определим минимальное число Рейнольдса:
2) Определим максимальное число Рейнольдса:
Задачи на гидравлический расчет трубопроводов
Трубопроводы — это система напорных труб, предназначенных для перемещения разнообразных жидкостей и газов [20].
В гидравлике при расчете трубопроводов их подразделяют на короткие и длинные. К первым относятся все трубопроводы, в которых местные потери напора превышают 5-10 % потерь напора по длине. При расчетах таких трубопроводов обязательно учитывают потери напора в местных сопротивлениях. Ко вторым относятся трубопроводы, в которых местные потери менее 5-10% потерь напора по длине. Их расчет ведется без учета местных потерь. Длинные трубопроводы можно разделить на простые и сложные.
Простыми трубопроводами называются последовательно соединенные трубопроводы одного или различных сечений, не имеющих никаких ответвлений.
К сложным трубопроводам относятся системы труб с одним или несколькими ответвлениями, параллельными ветвями, кольцевые и т.д.
Жидкость движется по трубопроводу благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Запас энергии должен быть создан работой насоса, давлением газа или за счет разности уровней жидкости.
Указания к решению задач:
Основными расчетными формулами для простого напорного трубопровода являются: уравнение Бернулли, уравнение постоянства расход, а также зависимости для определения потерь напора на трение по длине и в местных сопротивлениях [4, 21].
Если в трубопроводе необходимо обеспечить расход жидкости 
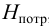
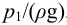
где 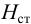
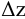
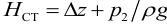
Потери напора выражают через расход 
где 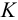
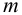
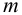
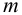
Для ламинарного течения при замене местных сопротивлений эквивалентными длинами сопротивление трубопровода равно
Для турбулентного режима течения жидкости в квадратичной области, используя формулу Вейсбаха-Дарси, и выражая в ней скорость через расход, получаем
Формулы (5.2), дополненная выражениями (5.3) и (5.4), является основной для расчета простых трубопроводов [4, 21].
Если трубопровод лежит в горизонтальной плоскости, а противодавление 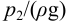
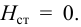
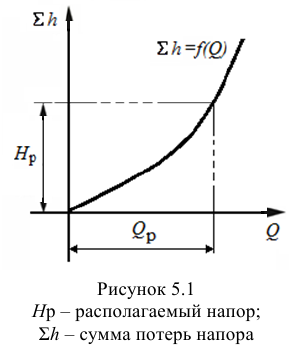
Выражение (5.5) называется гидравлической характеристикой трубопровода, которая показывает зависимость суммарной потери напора (или давления) в трубопроводе от расхода.
При ламинарном режиме течения гидравлическая характеристика представляет собой прямую линию, а при турбулентном в квадратичной области — параболу второй степени [20].
Задачи по расчету простого трубопровода можно разбить на три типа:
Тип 1. Известны: расход жидкости 
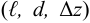
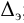
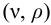
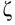
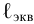
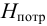
По известным значениям 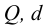
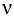
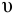
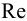
При ламинарном режиме искомый напор находится по формулам (5.2) и (5.3).
При турбулентном режиме задача решается с помощью формул (5.2) и (5.4). Определение зоны сопротивления производится с помощью формул Блазиуса или Альтшуля, в зависимости от шероховатости труб.
Тип 2. Известны: напор в начальном сечении (располагаемый напор 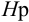

Расчет начинается с предположения о режиме течения жидкости. Так при течении маловязких жидкостей (воды, бензина, керосина и т.п.) целесообразно принимать режим течения турбулентным, при течении вязких жидкостей (масла, нефти и т.п.) — ламинарный.
При ламинарном режиме течения задача решается с помощью формул (5.2) и (5.3).
При турбулентном режиме в уравнениях (5.2) и (5.4) содержатся две неизвестные 
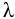
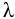
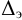
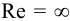
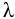
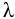
Вторым вариантом решения задачи является графоаналитический метод. Для этого необходимо построить гидравлическую характеристику трубопровода 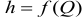
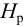

Гидравлическая характеристика трубопровода строится по данным расчета потерь напора при различных величинах расхода, т.е. решения задачи 1-го типа.
По известной величине напора 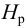
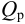
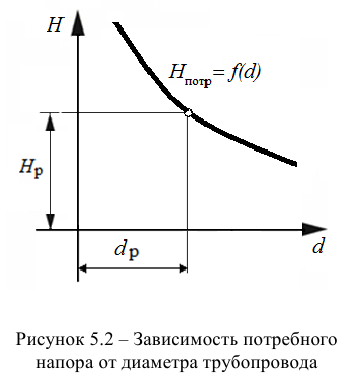
Тип 3. Известны следующие данные: расход жидкости 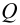
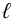
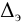
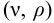
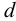
Задачу рекомендуется решать графоаналитическим способом (рис. 5.2), путем построения кривой взаимосвязи между потребным напором 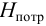
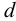
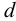
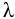
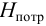
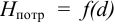
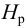
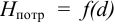
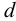
В конечном итоге принимается ближайший стандартный диаметр.
Расчет последовательно соединенного трубопровода
Последовательным называется такое соединение трубопроводов, при котором жидкость протекает по простым трубопроводам разного диаметра, последовательно соединенных в одну нитку (рис. 5.3). По всем участкам трубопровода протекает одинаковый расход жидкости 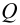
Потери напора в таком трубопроводе равны сумме всех местных потерь и потерь по длине:
где 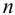
Если известны характеристики каждого участка трубопровода, то по ним можно построить характеристику всего последовательного соединения 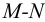
Возможно эта страница вам будет полезна:
Задача на гидравлический расчет сложного напорного трубопровода
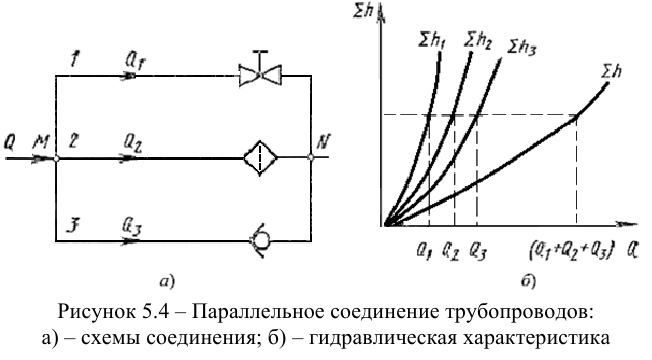
Сложный трубопровод обычно состоит из простых трубопроводов, которые соединены параллельно, либо имеет разветвления. Параллельным называется соединение трубопроводов, при котором жидкость, подходя к точке разветвления, течет по ответвлениям и далее снова сливается в один трубопровод, т.е. параллельно соединенные трубопроводы имеют общую точку разветвления и общий узел соединения (рис. 5.4).
Расход жидкости в основной магистрали равен сумме расходов в параллельных трубопроводах, а потери напора равны между собой:
где 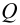
Потери напора можно выразить через соответствующие расходы:
где 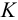
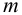
Для построения характеристики параллельного соединения нескольких трубопроводов следует сложить расходы характеристик этих трубопроводов при одинаковых ординатах (рис. 5.4, б).
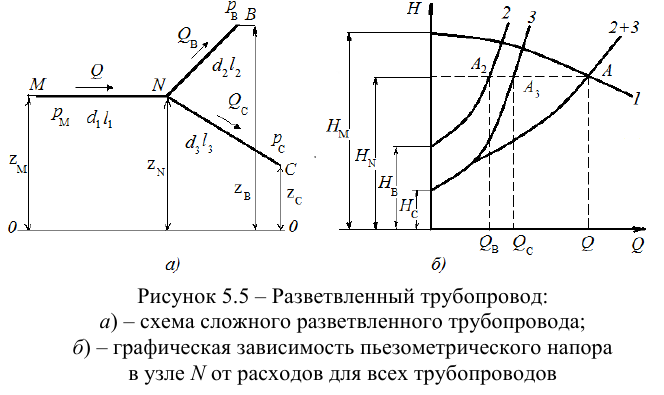
Разветвленным соединением называется совокупность нескольких простых трубопроводов, имеющих одно общее сечение — место разветвления (или смыкания) труб (рис. 5.5).
Алгоритм расчета разветвленного трубопровода включает следующие действия:
1) разбить сложный трубопровод на ряд простых;
2) рассчитать и построить кривые потребных напоров для каждого из простых трубопроводов;
3) провести графическое сложение параллельных участков;
4) провести графическое сложение последовательных участков.
ВНИМАНИЕ: при расчете разветвленного трубопровода необходимо идти от конечных точек к его начальной точке, т.е. против течения.
Приведем расчет разветвленного трубопровода (рис. 5.5). Трубопровод 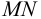
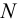
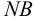
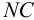
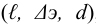
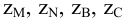
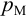
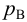
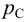
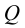
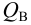
Величины пьезометрических напоров в точках 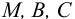
Для решения задачи составим систему уравнений, связывающих искомые расходы 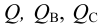
Представим три верхних уравнения системы (5.9), в виде системы уравнений пьезометрических напоров для трубопроводов 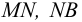
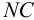
По уравнениям (5.10) строятся графические зависимости пьезометрического напора в узле 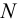
Зависимость суммарного расхода (уравнение 4 в системе (5.9)) в трубопроводах 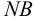
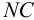
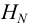
Значение напора 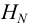
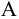
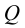
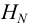
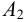
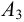
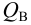
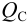
Теория из учебников и готовые задачи на продажу тут.
Задача на расчет трубопровода с насосной подачей жидкости
Основными понятиями для расчета таких трубопроводов являют-
- объемная подача насоса (подача
) — это объем жидкости, подаваемый насосом в единицу времени, т.е. объемный расход на выходе из насоса,
;
- напором насоса
называется механическая энергия, сообщаемая насосом единице веса перемещаемой жидкости, или разность удельных энергий жидкости на выходе и входе насоса, м;
- мощность насоса (потребляемая)
— это энергия, подводимая к насосу от двигателя за единицу времени, Вт;
- мощность насоса (полезная)
— это энергия, сообщаемая насосом за единицу времени протекающей через него жидкости весом
полезную мощность можно выразить:
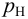
Мощность насоса 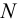
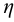
- характеристика насоса — графическое изображение зависимостей напора насоса
(или давления
), мощности
и КПД от подачи насоса
при постоянной частоте вращения;
- разомкнутый трубопровод с насосной подачей — это трубопровод, по которому жидкость перекачивается из одного места в другое;
- замкнутый (кольцевой) трубопровод с насосной подачей — это трубопровод, в котором циркулирует одно и тоже количество жидкости.
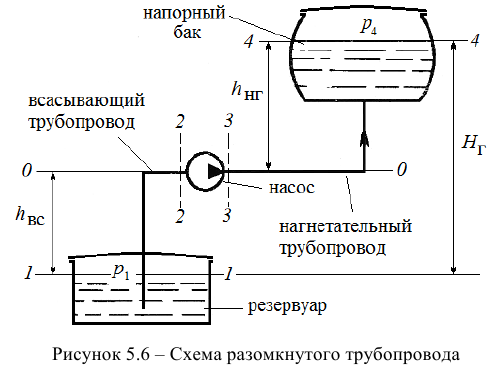
Рассмотрим решение задачи по расчету потребного напора разомкнутого трубопровода и построению на одном графике рабочей характеристики насоса и характеристики насосной установки.
Точка пересечения этих характеристик называется рабочей точкой.
1) Запишем уравнение Бернулли для потока жидкости во всасывающем трубопроводе для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0, совпадающей с горизонтальной осыо насоса (рис. 5.6):
где 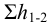
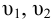
Удельная энергия перед входом в насос составит:
2) Запишем уравнение Бернулли для потока жидкости в нагнетательном трубопроводе для сечений 3-3 и 4-4 относительно плоскости сравнения 0-0, совпадающей с горизонтальной осыо насоса:
где 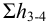
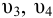
Так как скоростные напоры жидкости в баках 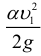
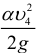
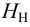
где 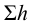
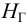
Обозначив через статический напор 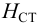
получим следующее выражение:
Таким образом, при установившемся режиме работы насоса его напор 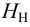
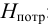
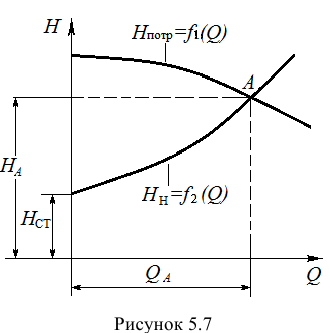
На полученном равенстве основан метод расчета трубопроводов, питаемых насосом, который заключается в построении на одном графике рабочей характеристики насоса 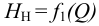
Точка пересечения этих характеристик называется рабочей точкой, в которой справедливо равенство (5.19).
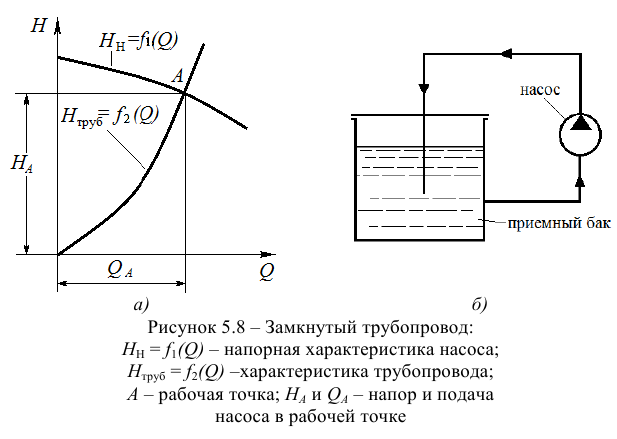
В случае замкнутого трубопровода (рис. 5.8) геометрическая высота подъема жидкости равна нулю (геометрический напор 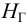
Следовательно, при значениях 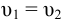
то есть, между потребным напором и напором, развиваемым насосом выполняется равенство (5.19).
Эти страницы вам могут пригодиться:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🎬 Видео
3.1 Основы гидростатики. ПрактикаСкачать

Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Решение задач на основное уравнение МКТ идеального газа | Физика 10 класс #29 | ИнфоурокСкачать

Урок 47 (осн). Расчет давления жидкости на дно и стенки сосудаСкачать

Основы гидродинамики и аэродинамики | основное уравнение гидростатики | для взрослыхСкачать

Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать

Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Гидростатическое давление . Решение задачСкачать

Гидравлика лекция 2Скачать

Решение задач по гидростатикеСкачать

ОСНОВНЫЕ ЗАКОНЫ ГИДРОСТАТИКИСкачать

Урок 48 (осн). Задачи на гидростатическое давление - 1Скачать

Физика 10 Идеальный газ Основное уравнение МКТ идеального газа Решение задачСкачать

Задача "Гидростатика"Скачать

3.1. Основы гидростатики. ЛекцияСкачать

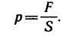
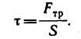
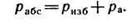
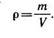

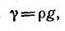
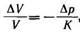
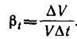
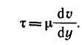
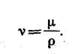
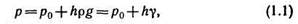

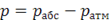
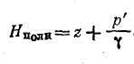
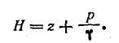
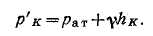
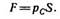




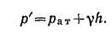
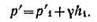
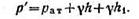
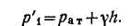
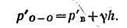
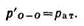

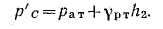



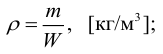
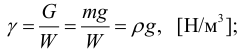
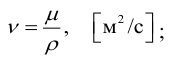
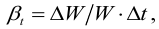
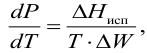
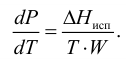
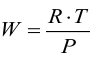
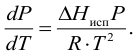
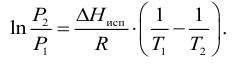
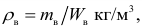
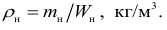
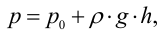
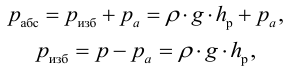
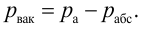
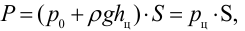
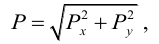
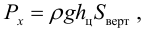
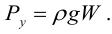
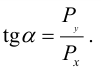
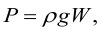
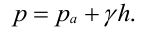
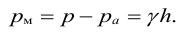
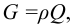
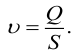
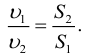
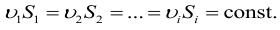
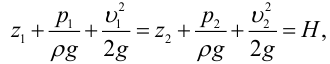
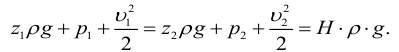
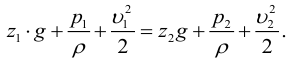
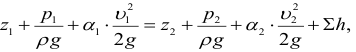
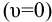 );
);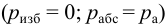 ;
;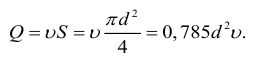
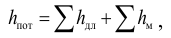
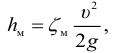
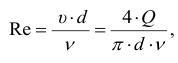
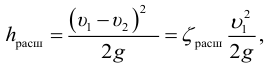
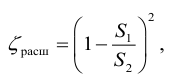
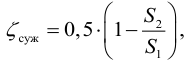
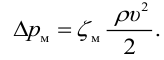
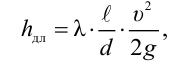
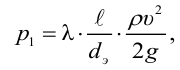
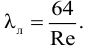
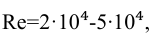
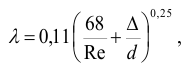
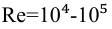
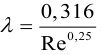
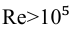
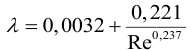
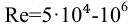
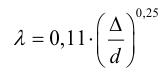
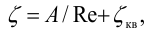
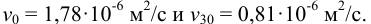
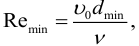
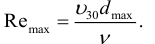
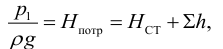
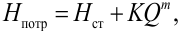
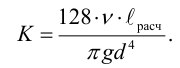
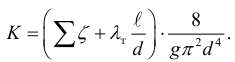
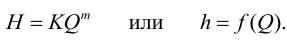
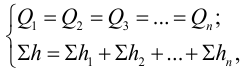
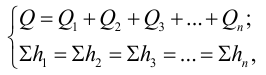
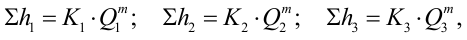
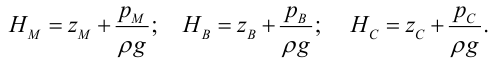
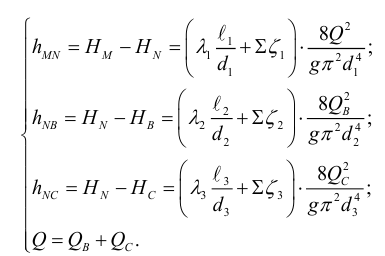
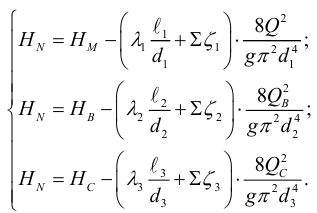
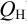 ) — это объем жидкости, подаваемый насосом в единицу времени, т.е. объемный расход на выходе из насоса,
) — это объем жидкости, подаваемый насосом в единицу времени, т.е. объемный расход на выходе из насоса, 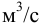 ;
;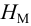 называется механическая энергия, сообщаемая насосом единице веса перемещаемой жидкости, или разность удельных энергий жидкости на выходе и входе насоса, м;
называется механическая энергия, сообщаемая насосом единице веса перемещаемой жидкости, или разность удельных энергий жидкости на выходе и входе насоса, м;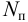 — это энергия, сообщаемая насосом за единицу времени протекающей через него жидкости весом
— это энергия, сообщаемая насосом за единицу времени протекающей через него жидкости весом 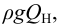 полезную мощность можно выразить:
полезную мощность можно выразить: