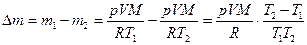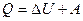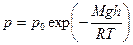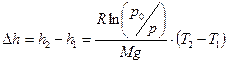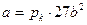9.1. В сосуде вместимостью V = 0,3 л находится углекислый газ, содержащий количества вещества ν = 1 моль при температуре Т = 300 К. Определить давление газа если: 1) газ реальный; 2) газ идеальный.
1) Газ реальный. Уравнение состояния реального газа уравнение Ван-дер-Ваальса для одного моля газа уравнение имеет вид:
Здесь R = 8,31 Дж/моль К ; а и b – поправки Ван-дер-Ваальса. Их значение определяется из справочных таблиц: а = 0,361 Н·м 4 / моль 2 ; b = 4,28·10 -5 м 3 / моль.
Из формулы (1) получим:
Проверка единиц измерения:
2). Газ идеальный. Применим уравнение Клаперона-Менделеева для одного моля газа: , откуда .
Проверка единиц измерения:
9.2. В сосуде вместимостью V1 = 1л содержится m =10 г азота. Определить изменение (ΔТ) температуры азота, если он расширяется в пустоту до объема V2 = 10л.
Решение: Процесс расширения газа в пустоту является адиабатическим, то есть происходит без теплообмена с окружающей средой: ΔQ = 0.
При расширении в пустоту работа не совершается: А = 0 .
Из первого начала термодинамики следует, что ΔU = 0, или U = const.
Внутренняя энергия газа остается постоянной.
Для реального газа внутренняя энергия определяется по формуле:
Здесь ν = – количество вещества, Cv – молярная теплоемкость газа, а – поправка Ван-дер-Ваальса, Vμ – объем одного моля газа.
Объём одного моля газа вычисляем по формуле:
Применим формулы (1) и (2) к решению задачи. До расширения
Выполним расчеты. Значение а возьмем из справочных таблиц: а = 0,135(Н м 4 )/моль 2 . Азот – двухатомный газ, поэтому его теплоемкость равна:
Проверка единиц измерения:
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Примеры решения задач по физике
Основные понятия и формулы.
Поведение реальных газов описывается уравнением состояния Ван-дер-Ваальса: для одного моля:

для ν молей газа:

где a, b – константы, зависящие от природы газа, которые приводятся в справочниках и приложениях к сборникам задач.
Внутренняя энергия ν молей реального газа:

Критические параметры вещества удовлетворительно описываются уравнением Ван-дер-Ваальса и выражаются через его параметры a и b:
Pкр = a/27b2, Vкр. = 3b, Tкр. = 8a/27bR (6.4)
Эффект Джоуля-Томпсона описывается соотношением:
где H1 и H2 – энтальпия газа до и после его расширения, соответственно.
Задачи на эту тему можно разделить на следующие группы:
а) задачи, которые учат работать с уравнением Ван-дер-Ваальса и позволяют получить ряд полезных соотношений;
б) задачи по описанию критического состояния вещества;
в) задачи на эффект Джоуля-Томпсона.
6.2. Примеры решения задач.
Один моль кислорода расширили до объема V1 = 1 л до V2 = 5 л при постоянной температуре T = 280 K. Вычислить количество поглощенного газом тепла, газ считать ван-дер-ваальсовым.
Дано: V1 = 1 л = 10-3 м3, V2 =5 л =5 10-3 м3, T = 280 К.
Решение. Для ответа на вопрос задачи запишем первое начало, в которое входит искомая величина Q. Элементарное тепло 

Согласно (6.3), внутренняя энергия реального газа:

а давление p из (6.1):

Подставим полученные выражения в (1), тогда:

Первый интеграл равен нулю, так как процесс идет при постоянной T. Из второго и третьего интегралов получим:

Видео:Уравнение Ван дер ВаальсаСкачать

Реальные газы. · Уравнение Ван-дер-Ваальса для одного моля газа
· Уравнение Ван-дер-Ваальса для одного моля газа
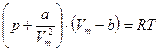
для произвольного количества вещества
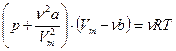
где a и b – постоянные Ван-дер-Ваальса; V – объем, занимаемый газом; Vm – молярный объем; р – давление газа на стенки сосуда; ν – количество вещества.
· Связь критических параметров – объема, давления и температуры газа – с постоянными Ван-дер-Ваальса
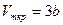
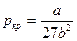
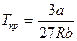
· Внутренняя энергия реального газа
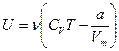
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1.В закрытом гараже объемом V1 = 80 м 3 хранился открытый сосуд с ацетоном объемом V2 = 0.5 л, который полностью испарился. Плотность ацетона ρ = 0.8·10 3 кг/м 3 . Вентиляция в гараже отсутствует. Определить количество ацетона в 1 м 3 воздуха.
Решение: Количество паров ацетона в 1 м 3 воздуха равно
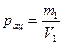
где 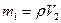
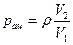
Подставив числовые данные, получим
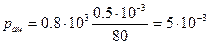
Пример 2.Сколько молекул воздуха находится в комнате объемом 240 м 3 при температуре 15 0 С и давлении 750 мм.рт.ст.?
Решение: Чтобы использовать объединенный закон газового состояния, сравним между собой состояния данной массы воздуха при заданных (p1, V1, T1) и нормальных (p0, V0, T0) условиях:
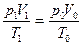
Поскольку объем воздуха при нормальных условиях 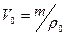
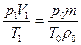
откуда 
Найдем, сколько молей содержится в данной массе воздуха:
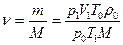
Поскольку в одном моле любого газа, в том числе и воздуха, содержится число молекул, равное постоянной Авогадро, то:
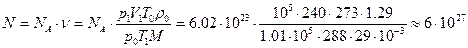
Пример 3. Из баллона со сжатым водородом вместимостью V = 10 л вследствие неисправности вентиля утекает газ. При температуре t1 = 7 0 С барометр показывает p = 51 атм. Показание барометра не изменилось и при температуре t2 = 17 0 С. Определите, сколько газа утекло.
Решение: Используя уравнение Клапейрона-Менделеева
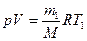
найдем первоначальную массу водорода
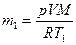
Аналогично найдем массу водорода m2 после утечки:
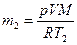
Следовательно, масса утекшего газа:
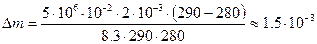
Пример 4.Давление атомарного водорода в космическом пространстве примерно р = 1,7·10 -15 Па при температуре Т = 125 К, эффективный диаметр его молекул dэф = 0,22 нм. Найти, какое время t в среднем движется молекула водорода между последовательными столкновениями.
Решение: Время между последовательными столкновениями можно найти, разделив среднюю длину свободного пробега молекулы на ее среднюю арифметическую скорость:
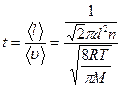
Концентрация молекул n связана с давлением р формулой 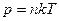
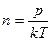
Тогда время между последовательными столкновениями молекул водорода найдем как: 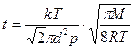
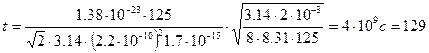
Пример 5.Кислород массой m = 2 кг занимает объем V1 = 1 м 3 и находится под давлением р1 = 0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V2 = 3 м 3 , а затем при постоянном объеме до давления р3 = 0,5 МПа. Найти изменение внутренней энергии ΔU газа, совершаемую им работу А и теплоту Q, переданную газу.
Решение: Изменение внутренней энергии газа:
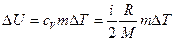
где i = 5 – число степеней свободы молекул кислорода; ΔТ = Т3 – Т1 – разность температур газа в конечном (третьем) и начальном состояниях.
Начальную и конечную температуру газа найдем из уравнения Клапейрона-Менделеева
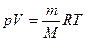
откуда 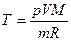
Работа расширения газа при постоянном давлении выражается формулой:
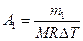
Работа газа, нагреваемого при постоянном объеме, равна нулю:
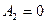
Следовательно, полная работа, совершаемая газом, равна:
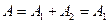
Согласно первому началу термодинамики, теплота, переданная газу, равна сумме изменения внутренней энергии и работы:
Произведем все вычисления, учтя, что для кислорода М = 32·10 -3 кг/моль.
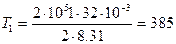
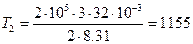
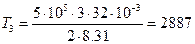
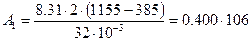
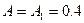
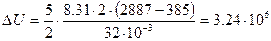
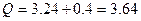
Пример 6.Барометр в кабине летящего самолета все время показывает одинаковое давление р = 79 кПа, благодаря чему летчик считает высоту h1 полета неизменной. Однако температура воздуха за бортом самолета изменилась с 5 0 С до 1 0 С. Какую ошибку Δh в определении высоты допустил летчик? Давление р0 у поверхности Земли считать нормальным.
Решение: Для решения задачи воспользуемся барометрической формулой
Барометр может показывать неизменное давление при различных температурах Т1 и Т2 за бортом только в том случае, если самолет находится не на высоте h (которую летчик считает неизменной), а на некоторой другой высоте h2.
Запишем барометрическую формулу для этих двух случаев:
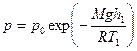
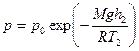
Найдем отношение р0/р и обе части полученного равенства прологарифмируем:
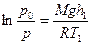
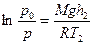
Из полученных соотношений выразим высоты h1 и h2 и найдем их разность:
Подставим значения и произведем вычисления:
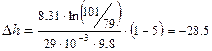
Знак «–» означает, что h2 7 Дж/кг. Температура котла t1 = 200 0 С, температура холодильника t2 = 58 0 С. Найти фактический ηф КПД этой машины. Определить во сколько раз КПД идеальной ηид тепловой машины, работающей по циклу Карно при тех же температурах нагревателя и холодильника, превосходит КПД этой паровой машины ηф.
Решение: КПД реальной паровой машины (фактический КПД) определяется отношением работы, совершенной этой машиной за некоторое время, к количеству теплоты Q1, которое отдано нагревателем за это время:
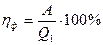
Работу, совершаемую паровой машиной, можно определить произведением мощности на время ее работы: 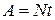
Паровая машина отдает количество теплоты Q1, которое выделит сгоревший уголь массой m. Это количество теплоты равно:
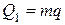
Тогда фактический КПД паровой машины определим как:
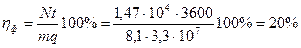
КПД идеальной тепловой машины, работающей по циклу Карно, определяется формулой:
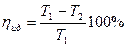
Разделив (2) на (1) мы ответим на второй вопрос задачи:
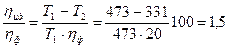
Пример 9.Какую температуру Т имеет масса m = 2г азота, занимающего объем V = 820 см 3 при давлении р = 0,2 МПа? Для азота Тк = 126 K, рк = 3,4 МПа.
Решение: Реальные газы подчиняются уравнению Ван-дер-Ваальса: 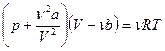
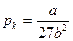

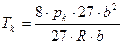
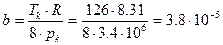
💡 Видео
Основы теплотехники. Реальные газы. Уравнение Ван дер Ваальса. Решение задач.Скачать

Уравнение Ван-дер-Ваальса и опыт Джоуля и ТомсонаСкачать

Уравнение Ван дер Ваальса. Часть 3. Внутренняя энергия реального газа. Фазовые переходы 1 рода.Скачать

Уравнение Ван-дер-Ваальса | Газы.Молекулярно-кинетическая теория | Химия (видео 8)Скачать

Реальные газы. Изотермы Эндрюса и Ван-Дер-Ваальса. Метастабильные состоянияСкачать

Реальный газ Уравнение Ван-Дер-ВаальсаСкачать

Уравнение Ван дер Ваальса. Часть 2. Критические параметры. Критическое состояние.Скачать

Уравнение Ван дер Ваальса. Часть 1. Межмолекулярные взаимодействия. Изотермы Ван дер Ваальса.Скачать

Урок 195. Изотермы реального газаСкачать

Уравнение Ван-дер-Ваальса (вывод и применение). By Bogatov N.A.Скачать

Уравнение состояния идеального газа. 10 класс.Скачать

Решение задач с помощью уравнений.Скачать

Решение задач с помощью уравненийСкачать

Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать

Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать

Решение задач на основное уравнение МКТ идеального газа | Физика 10 класс #29 | ИнфоурокСкачать