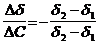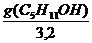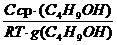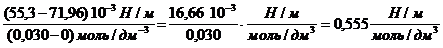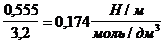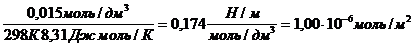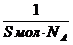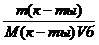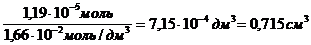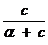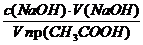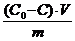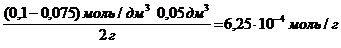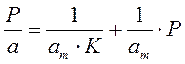Решение задач на уравнение ленгмюра (3 видео)

Содержание

Примеры решения типовых задач
Уравнение изотермы адсорбции Ленгмюра
Молекулярно-кинетические свойства коллоидных систем
🔍 Видео

Видео:Решение задач с помощью уравнений. Видеоурок 29. Математика 6 классСкачать

Примеры решения типовых задач

Пример 1

Расчет величины поверхностной активности ПАВ по изменению поверхностного натяжения; расчет величины поверхностной активности гомолога по правилу Траубе, расчет величины адсорбции ПАВ в заданном интервале концентраций.

Поверхностное натяжение водного раствора пентанола с концентрацией 0,030 моль/дм 3 равно 55,3 10 -3 Н/м при 298 К. Оцените величину адсорбции бутанола из раствора с концентрацией 0,015 моль/дм 3 при той же температуре.

Решение. Найдем поверхностную активность пентанола g(С5Н11OН) в интервале концентраций C1 = 0 (т.е. чистый растворитель) — C2= 0,030 моль/дм 3 :

g(С5Н11OН) = —

— коэффициент поверхностного натяжения воды, справочная величина (табл.11.02.).

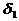
В соответствии с правилом Траубе поверхностная активность бутанола, предшествующего члена гомологического ряда предельных одноатомных спиртов, будет в тех же условиях примерно в 3,2 раза меньше:

g(С4Н9OН) =

Поскольку концентрация раствора бутанола равна 0,015 моль/дм 3 является серединой интервала, в котором рассчитывалась поверхностная активность, величина адсорбции из этого раствора рассчитывается по уравнению Гиббса:

Г(C4H9OH) =

g(С5Н11OН) =

g(С4Н9OН) =

Г(С4Н9OН) =

Ответ: величина адсорбции бутанола приблизительно равна 1 10-6 моль/м2.

Пример 2

Расчет длины и площади поперечного сечения молекулы по величине предельной адсорбции.

Площадь поперечного сечения молекулы пальмитиновой кислоты равна2,1×10 -19 м 2 . Определите величину предельной адсорбции пальмитиновой кислоты на границе бензольный раствор-воздух. Вычислите объем раствора, содержащего 4,24 г кислоты в 1 л бензола, требуемый для покрытия монослоем (после испарения бензола) 1,5 м 2 водной поверхности.

Решение.Величину предельной адсорбции данного вещества рассчитывают по уравнению:

Г_max =

Для покрытия площади S монослоем молекул с площадью поперечного сечения S мол требуется S/S мол молекул. Количество вещества, соответствующее этому числу молекул, рассчитывают по соотношению:

n= 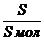: NA

Молярная концентрация имеющего раствора пальмитиновой кислоты равна:

С_(к-ты) =

Требуемый объем раствора равен: Vp = 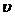/с

Г max = 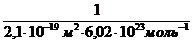= 7,9 10-6моль/м2

n = 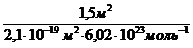= 1,19 10-5моль

с (к-ты) = 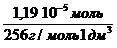= 1,66 10-2моль/дм3

V =

Ответ: Г max = 7,9 10-6 моль/м 2 Vр = 0,715 мл

__________________________________________________________________________________

Пример 3

Расчет величины адсорбции по уравнению Ленгмюра при заданных константах.

Экспериментально установлено, что максимальная величина адсорбции ПАВ (M_r = 60) некоторым адсорбентом составляет 5,0×10 -3 моль/г; величина a равна 0,06 моль/дм 3 . Сколько граммов вещества адсорбировалось из раствора с равновесной концентрацией 0,1 моль/дм 3 двумя граммами данного адсорбента?

Решение. По уравнению Ленгмюра рассчитывают величину адсорбции ПАВ:

а = a max

Количество адсорбированного вещества на адсорбенте массой 2 г будет в 2 раза больше.

Масса адсорбированного вещества будет равна:

m (ПАВ) = n(ПАВ) М(ПАВ)

а = 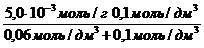= 3,1 10-3моль/г

n(ПАВ) = 3,1×10-3моль/г 2 г = 6,2 10-3моль

m(ПАВ) = 6,2×10-3моль 60 г/моль = 0,37 г

Ответ: масса адсорбированного вещества равна 0,37 г.

Пример 4

Расчет величины адсорбции на твердом адсорбенте по изменению концентрации адсорбтива.

Раствор уксусной кислоты объемом60 см 3 раствора уксусной кислоты с концентрацией 0,1 моль/дм 3 взболтали с 2 г адсорбента. После достижения равновесия пробу раствора объемом 10 см 3 оттитровали раствором гидроксида натрия с = 0,05 моль/дм 3 . На титрование затрачено 15,0 см 3 титранта. Вычислите величину адсорбции уксусной кислоты.

Решение. Равновесная концентрация уксусной кислоты равна (по результатам титрования):

(СН3СООН) =

Величину адсорбции рассчитывают по:

а =

с(СН3СООН) = 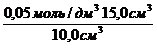= 0,075 моль/см3

а =

Видео:Математика 6 класс (Урок№51 - Решение задач с помощью уравнений. Часть 1.)Скачать

Уравнение изотермы адсорбции Ленгмюра

Конечно, предположение, что молекулы адсорбируются с одинаковой вероятностью на любых участках поверхности, в том числе и уже занятых ранее — слишком грубое допущение, пригодное лишь для очень малых степеней покрытия.

Теория Ленгмюра позволяет учесть наиболее сильные отклонения от закона Генри, что связано с ограничением адсорбционного объема или поверхности адсорбента. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества. Это положение уточняется следующими утверждениями.

1) Адсорбция локализована на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбента — образуется мономолекулярный слой.

2) Адсорбционные центры энергетически эквивалентны — поверхность адсорбента эквипотенциальна.

3) Адсорбированные молекулы не взаимодействуют друг с другом.

Простейший вывод уравнения Ленгмюра, данный Кисилевым, основан на рассмотрении химического (в случае хемосорбции) или квазихимического (в случае физической адсорбиии) равновесия молекула газа + свободное место↔адсорбированная молекула.

Для обычного выражения константы равновесия через концентрации участников рассматриваемого процесса необходимо условиться о способах их выражения. Концентрация адсорбированных молекул может быть выражена не только числом адсорбированных молекул на 1 м 2 поверхности, но и в относительных единицах через долю занятой поверхности (степень заполнения поверхности) θ. Тогда, в тех же единицах, концентрация свободных мест 1-θ. Концентрация молекул газа (а молях на миллилитр) может быть заменена пропорциональной ей величиной давления Р (равновесное давление адсорбата в объеме фазы, граничащей с адсорбентом). Такая свобода в выборе единиц рассматриваемых концентраций обусловлена тем, что соответствующие константы пропорциональности могут быть объединены с константой равновесия. Итак, константа равновесия

. (2.6)

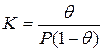
Решение этого уравнения относительно θ приводит к выражению

. (2.7)

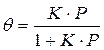
Если а, как и раньше, есть величина адсорбции (моль/см 2 или см 3 /г), а a_m — величина адсорбции, соответствующая полному заполнению поверхности (емкость монослоя, моль/см 2 ), то степень заполнения θ=a/a_m, (2.8)

т.е. 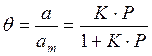, (2.9)

отсюда 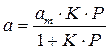(2.10)

В такой форме уравнение Ленгмюра широко известно. Оно содержит две константы: a_m, кратко называемая емкостью монослоя, и K — константа, зависящая от энергии адсорбции и температуры.

Итак, уравнение Ленгмюра – это уравнение монослойной адсорбции на однородной поверхности в отсутствие сил притяжения между молекулами адсорбата.

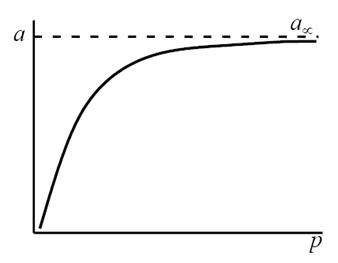
Посмотрим, какую форму примет уравнение при крайних значениях поверхностной концентрации адсорбированного вещества.

В области малых концентраций, т.е. при малых давлениях, КР >1, и единицей в знаменателе можно пренебречь:

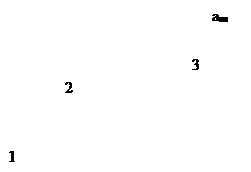
т.е. величина адсорбции стремится к пределу, при котором она уже практически не зависит от давления (участок 3 изотермы адсорбции). В промежуточной области (участок 2) зависимость адсорбции от давления описывается самим уравнением (2.10).

Рис. 2.5. Три участка изотермы адсорбции Ленгмюра

Таким образом, по модели Ленгмюра, вначале адсорбция растет пропорционально давлению газа, затем, по мере заполнения мест на поверхности, этот рост замедляется и, наконец, при достаточно высоких давлениях рост адсорбции практически прекращается, так как покрытие поверхности становится весьма близким к монослойному. Необходимо подчеркнуть, однако, что по этой модели завершение образования монослоя происходит лишь при бесконечно высоком давлении. Форма изотермы адсорбции, предсказываемая уравнением Ленгмюра, экспериментально наблюдается в случае химической адсорбции на однородных поверхностях. Для физической адсорбции такое соответствие наблюдается только в начальной области изотермы. При больших заполнениях не получается предсказываемого теорией приближения к насыщению и изотерма продолжает подъем с ростом давления, причем она становится даже более крутой.

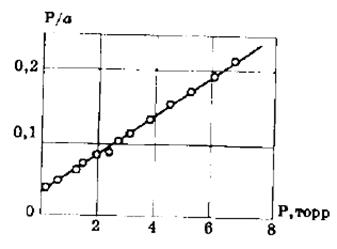
Для удобной проверки приложимости уравнения Ленгмюра к экспериментальным данным преобразуем его в линейную форму. Разделим обе части уравнения (2.10) на Р:

. (2.13)

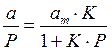
Перевернем дроби по обе части равенства:

. (2.14)

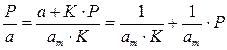
Если по оси абсцисс откладывать Р, а на оси ординат Р/а, то в случае выполнимости уравнения Ленгмюра экспериментальные точки должны укладываться на прямую. Начальной ординатой будет 1/(а_m∙К), тангенсом угла наклона прямой 1/а_m. Из того и другого выражения легко вычислить обе константы a_m и К. Пример такого построения показан на рис. 2.6, где экспериментальные точки для адсорбции бензола на графитированной саже, в соответствии с указанными ранее, легли па прямую только в области малых давлений (до Р/Р₀ =0.1).

Рис. 2.6. Изотерма адсорбции бензола при 20 о С на графитированной саже в координатах линейной формы уравнения Ленгмюра

Имеется немало примеров, когда уравнение Ленгмюра не выполняется. Объясняется это тем, что не оправдываются оба допущения теории об однородности поверхности и отсутствии взаимодействия молекул, особенно первое из них. Тот факт, что имеются случаи адсорбции на реальных неоднородных поверхностях, когда уравнение Ленгмюра все же удовлетворительно описывает экспериментальные данные, Брунауер объясняет тем, что в некотором интервале адсорбция происходит не на всей поверхности адсорбента, а только на части ее, именно на местах с примерно одинаковой теплотой адсорбции. Тогда в этом интервале уравнение Ленгмюра будет справедливо. После того, как эти места заполнены, начинает заполняться следующая серия мест с меньшей теплотой адсорбции. Поэтому для совокупности всех мест поверхности уравнение Ленгмюра может быть непригодно, а для части этих мест — справедливо. Отсюда, выполнимость его для разных адсорбентов зависит от соотношения участков с разной теплотой адсорбции.

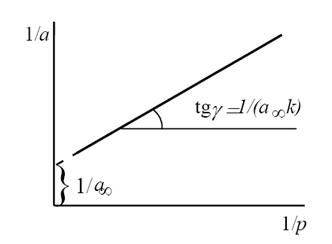
Константы уравнения (2.10) K и a_m могут быть определены графическим способом (рис. 2.7). Для этого уравнение Ленгмюра приводят к следующему линейному виду, разделив единицу на уравнение (2.10):

(2.15)

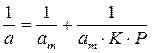
Рис. 2.7. Линейная форма уравнения изотермы Ленгмюра (a_∞=a_m)

Зная емкость монослоя, можно определить удельную поверхность адсорбента S_уд (м 2 /г или см 2 /г) если известна площадь ω, занимаемая частицей в плотном адсорбционном слое (площадь, занимаемая одной молекулой азота в адсорбционном слое ω = 0.162 нм 2 ):

, (16)

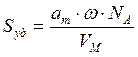
где а_m — емкость монослоя — это количество адсорбата, которое может разместиться в полностью заполненном адсорбционном слое толщиной в 1 молекулу — монослое – на поверхности единицы массы (1г) твердого тела; ω — средняя площадь, занимаемая молекулой адсорбата в заполненном монослое, N_A — число Авогадро (6,022·10 23 молекул/моль); V_M — молярный объем адсорбата (газа) (V_M = 22,41 л/моль=22,41∙10 -3 м 3 /моль).

Уравнение Ленгмюра можно использовать только при адсорбции в мономолекулярном слое. Это условие выполняется при хемосорбции, физической адсорбции газов при меньшем давлении и температуре выше критической.

Однако в большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и поэтому остается возможность влияния поверхностных сил на второй и т.д. адсорбционные слои. Это реализуется в том случае, когда газы и пары адсорбируются при температуре ниже критической, т.е. образуются полимолекулярные слои на поверхности адсорбента, что можно представить как вынужденную конденсацию В этом случае используют уравнение БЭТ (Брунауер –Эммет — Теллер).

Пример 2.1. При адсорбции азота на активированном угле при 220К получены следующие данные:

Р, Па 5310 9800 18000 33000 70000

a, cм 3 /г 7 14 23 32 51

Плотность газообразного азота ρ=1,2506 кг/м 3 . Площадь, занимаемая одной молекулой азота в насыщенном монослое, составляет ω = 0.162 нм 2 . V_M — молярный объем адсорбата (газа) (V_M = 22,41 л/моль=22,41∙10 -3 м 3 /моль).

Постройте изотерму адсорбции в линейных координатах. Графически определите константы а_m и К уравнения Ленгмюра, пользуясь которыми, постройте изотерму Ленгмюра. Определите удельную поверхность активированного угля S_уд.

Решение. Линейная форма уравнения Ленгмюра выражается (2.15):

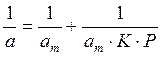
Определим 1/а_m и 1/ р:

(1/р)·10 -3 , Па 0,1883 0,1020 0,0556 0,0303 0,0143

1/а·, см 3 /г 0,143 0,071 0,043 0,031 0,020

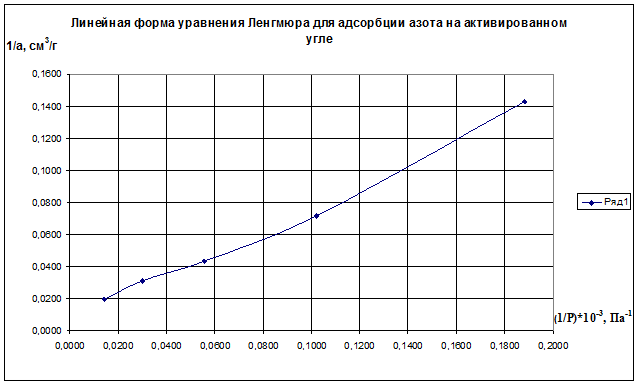
Строим график зависимости 1/а=f(1/р)∙10 -3 (рис.2.8). По графику находим 1/а_m как отрезок, отсекаемый прямой на оси ординат, для чего необходимо продлить полученную прямую до пересечения с осью ординат.

Рис.2.8. Линейная форма уравнения Ленгмюра для адсорбции азота на активированном угле

Уравнение прямой y=a+bx, имеет следующее формульное выражение:

Это выражение может быть определено с помощью регрессионного анализа в Microsoft Excel (встроенного пакета Анализ данных — Регрессия по значениям 1/а_m и 1/ р).

Из уравнения получим 1/a_m=0,00698 г/см 3 .

Откуда получим: a_m=143,35 см 3 /г.

Далее находят тангенс угла наклона прямой к оси абсцисс tgα=1/(a_m∙K) по графику (или по уравнению регрессии). tgα=0,70099. Тогда, зная значения a_m и tgα, можно определить K=9,95 кг/м 3 .

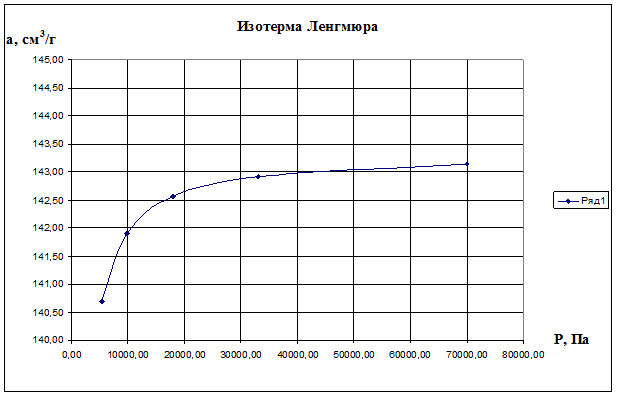
Теперь, зная константы а_m и К уравнения Ленгмюра, построим изотерму Ленгмюра, для чего рассчитаем по формуле (2.10) значения а для различных значений Р и получим:

Р, Па 5310 9800 18000 33000 70000

a, cм 3 /г 140,69 141,90 142,56 142,92 143,15

По данным значениям построим изотерму Ленгмюра а=f(P), представлена на рис.2.9.

Рис. 2.9. Изотерма Ленгмюра а=f(P)

По формуле (2.16) рассчитаем удельную поверхность активированного угля: 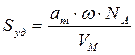и получим S_уд=624,05 м 2 /г.

В случае, когда известна плотность вещества (адсорбента) ρ и молярная масса M, а не известен V_M — молярный объем адсорбата удельную поверхность вещества (активированного угля) находят по формуле:

где a_m выражают в моль/кг.

Для азота М= 0,0280 кг/моль, ρ=1,2506 кг/м 3 .

Из расчетов видно, что два способа расчета S_уд дают почти одинаковые результаты.

Пример 2.2. Удельная поверхность непористой сажи равна 73,7м 2 /кг. Рассчитайте площадь, занимаемую молекулой бензола в плотном монослое, исходя из данных об адсорбции бензола на этом адсорбенте при 293 К.

Р, Па 1,03 1,29 1,74 2,50 6,67

а∙10 2 , моль/кг 1,57 1,94 2,55 3,51 7,58

Предполагается, что изотерма адсорбции описывается уравнением Ленгмюра.

Решение. Используем линейную форму записи уравнения Ленгмюра, заданную формулой (2.14):

Рассчитываем значения Р/а:

(Р/а)∙10 -2 , Па∙кг/моль 0,656 0,668 0,68 0,712 0,879

Р, Па 1,03 1,29 1,74 2,50 6,67

По этим данным строим график в координатах уравнения Ленгмюра в линейной форме P/a=f(P).

Из графика находим а_m= Р/(Р/а) = 25,2∙10 -2 моль/кг.

Удельная поверхность адсорбента связана с емкостью слоя а_m, выраженного в моль/кг, соотношением: S_уд=a_m∙ω∙N_A (2.18)

Площадь, занимаемая молекулой бензола в плотном монослое, равна

ω = S_уд/(a_m N_A) ==73,7 10 3 /(6,02 10 23 ∙25,210 -2 )=0,49∙10 -18 м 2 =0,49 нм 2 .

Видео:Уравнение ЛенгмюраСкачать

Молекулярно-кинетические свойства коллоидных систем

Примеры решения типовых задач

Задача 1.Определить радиус шарообразных частиц золя сульфида мышьяка As₂S₃ массовой концентрации 6,7 кг/м 3 , плотностью 2,8 г/см 3 , если при 20 0 С осмотическое давление дисперсной системы составляет 0,07 Па.

Решение.Сочетая уравнения p = и n= , получим формулу для осмотического давления

p = ,

откуда определяем выражение для радиуса частиц с учетом того, что
r = 2,8 г/см 3 = 2,8 × 10 3 кг/м 3 , температура Т = 293 К

м.

Задача 2. Определить коэффициент диффузии и среднее смещение частиц в суспензии кварца в воде за 7 с, диаметр частиц составляет 0,5 мкм, вязкость дисперсионной среды 10 -3 Па ×с, температура 20 0 С.

Решение. С учетом того, что радиус частиц r = 0,25 × 10 -6 м, температура Т = 293 К

D = 8,59× 10 -13 м 2 /с.

Среднее смещение определяется по формуле

= 3,47 × 10 -6 м.

Оптические свойства коллоидных систем

Примеры решения типовых задач

Задача 1.С помощью нефелометра определили, что мутность гидрозоля полистирольного латекса в 3 раза больше мутности стандартного золя. Средний диаметр частиц стандартного золя 40 нм. Определить радиус частиц гидрозоля мастики, если концентрации золей одинаковы.

Р е ш е н и е. Для расчета радиуса исследуемого золя используем уравнение r_х= r_ст× , где r_ст = , а d = 40 нм = 40 × 10 -9 м.

r_х= r_ст× м.

Задача 2. Методом поточнойультрамикроскопии в объеме
4,85 × 10 — 11 м 3 подсчитано 85 частиц аэрозоля водяного тумана. Каков средний радиус частиц, если концентрация аэрозоля 3,15 × 10 — 5 кг/м 3 .

Р е ш е н и е. Радиус частиц рассчитывают по уравнению , где r = 10 3 кг/м 3 .

м.

Поверхностные явления в коллоидных системах

Примеры решения типовых задач

Задача 1.Вычислить удельную поверхность единицы объема и единицы массы золя сульфида мышьяка As₂S₃, средний диаметр частиц которого равен 1,6 мкм, плотность дисперсионной среды 3,43 × 10 3 кг/м 3 .

Р е ш е н и е.Согласно формуле S_уд(_v₎ = , м — 1 , определяют удельную поверхность единицы объема золя с учетом того, что

S_уд(_v₎ = = =3,75 × 10 6 , м — 1 .

Далее определяют удельную поверхность единицы массы золя

S_уд(_m₎ = = =1,093 × 10 3 м 2 /кг.

Задача 2.Вычислить суммарную площадь поверхности платины массой 3 × 10 -3 кг, раздробленной на правильные кубики с длиной ребра 10 -8 м и плотностью 21,4 г/см 3 .

Р е ш е н и е.Для определения суммарной площади воспользуемся формулой S_сум = nS_куб. Площадь одной кубической частицы определяют по формуле:

S_куб = 6l 2 = 6 × (10 — 8 ) 2 = 6 × 10 — 16 м 2 .

Чтобы определить число частиц n в объеме системы используем формулу V_сум = nV_куб, откуда .

V_сум= .

V_куб = l 3 = (10 — 8 ) 3 = 10 — 24 м 3 .

= = 1,4 × 10 17 частиц.

S_сум = nS_куб = 1,4× 10 17 × 6 × 10 — 16 = 84 м 2 .

Задача 3.Во сколько раз изменится запас свободной поверхностной энергии водяного тумана, если радиус его капелек уменьшится от 1 мм до 10 — 7 м.

Р е ш е н и е. Используют формулу

Так как S_уд(_v₎ = , то

Запас свободной поверхностной энергии водяного тумана увеличится в 10000 раз.

Задача 4.120 г пальмитиновой кислоты СН₃(СН₂)₁₄СООН нанесли на чистую водную поверхность. Площадь, занимаемая одной частицей составляет 1,8 × 10 — 21 м 2 . Определить суммарную площадь поверхности.

Р е ш е н и е. Для определения суммарной площади поверхности используем формулу S_сум = nS_{частицы}. Определим число частиц пальмитиновой кислоты n по формуле

n = n×N_A, где n — количество вещества кислоты, моль; N_А – постоянная Авогадро.

n = моль, М – молярная масса пальмитиновой кислоты.

n = 0,47× 6,02 × 10 23 = 2,82 × 10 23 .

S_сум = 2,82× 10 23 × 1,8 × 10 — 21 = 507,6 м 2 .

Адсорбция

Примеры решения типовых задач

Задача 1. Найти величину адсорбции органической кислоты на поверхности раздела водный раствор/воздух, степень заполнения поверхности и удельную поверхность адсорбента при 17 0 С и концентрации 0,7 × 10 3 моль/м 3 по константам уравнения Шишковскогоа = 12,5 × 10 -3 и b = 7,73 × 10 -3 . Площадь, занимаемую одной молекулой кислоты принять равной 15,85 × 10 -19 м 2 .

Р е ш е н и е. Величину адсорбции найдем по уравнению изотермы Ленгмюра. Для этого определим величину Г_¥ с учетом того, что Т = 17 0 С = 290 К:

Г_¥ = моль/м 2 .

Рассчитываем величину адсорбции

Г = моль/м 2 .

Степень заполнения вычисляют по формуле:

q = .

Удельную поверхность адсорбента находят с помощью выражения:

S_уд = Г_¥N_AS₀= 5,19× 10 — 6 × 6,02 × 10 23 × 15,85 × 10 — 19 = 4,95 м 2 .

Задача 2.Определить константы уравнения Ленгмюра и адсорбцию СО₂ на слюде, а также степень заполнения q при Р =8 Па, если при Т =155 К получены следующие результаты:

Р, Па	0,48	1,19	2,06	9,8
Г, моль/см 2	1,22 × 10 — 10	1,95 × 10 — 10	2,55 × 10 — 10	3,62 × 10 — 10

Р е ш е н и е. Согласно уравнению Ленгмюра, является угловым коэффициентом прямой зависимости между и Р и, следовательно,
Г = ctgj, где j — угол наклона прямой. Вычисляем величины :

Р, Па	0,48	1,19	2,06	9,8
	0,39 × 10 10	0,61 × 10 10	0,81 × 10 10	2,7 × 10 10

По полученным данным строим график, отложив на оси абсцисс Р, а на оси ординат . Как видно из графика,
Г = ctgj = моль/см 2 .

Зависимость от Р.

Отрезок, отсекаемый на оси ординат, равен = 0,25 × 10 10 , откуда

b= .

Вычислим величину Г при 8 Па по уравнению:

Г = = 4,03 × 10 — 10 моль/см 2 .

Степень заполнения поверхности определяем по формуле:

q = .

Задача 3. Найти константы уравнения Фрейндлиха, если при адсорбции уксусной кислоты на активированном угле получены следующие данные

С, моль/л	0,0024	0,0073	0,0204
Г, моль/г	2,9 × 10 — 4	4,6 × 10 — 4	8,5 × 10 — 4

Р е ш е н и е. Воспользуемся уравнением изотермы адсорбции Г = kС a . Константы уравнения Фрейндлиха определяются графически после логарифмирования. Находим логарифмы концентрации кислоты и величин Г:

lgC	-2,62	-2,14	-1,69
lgГ	-3,54	-3,34	-3,07

Зависимость lgГ-lgC показана на рис. ниже

Согласно графику, lgk = -2,22, следовательно, k = 10 — 2,22 = 6,02 × 10 — 3 .

tgj = 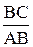= = 0,52, следовательно, a = 0,52.

Задача 4. При адсорбции криптона на серебре при 77,5 К получены следующие результаты:

Р, мм.рт.ст.	0,0992	0,1800	0,3686	0,5680	0,6843
V, см 3 /г	0,0127	0,0150	0,0176	0,0190	0,0198

Рассчитать константы уравнения БЭТ V_mи с,удельную поверхность катализатора S_y_д,приняв площадь, занимаемую одной молекулой криптона, равной 19,5 × 10 — 20 м 2 , плотность криптона при 0° С 3,739 × 10 — 3 г/см 3 , давление насыщенного пара криптона 2,57 мм.рт. ст.

Р е ш е н и е.Согласно уравнению изотермы адсорбции БЭТ, прямолинейная зависимость получается в координатах — .

	0,0385	0,0700	0,1430	0,2200	0,2660
	3,16	5,02	9,50	14,93	18,33

На основании полученных данных строим график. Из графика находим тангенс угла наклона прямой:

tgj = = . (а)

Отрезок, отсекаемый на оси ординат, равен . (б)

Решая совместно уравнения (а) и (б), получаем значения с = 134,4 и
V_m = 0,0149 см 3 /г.

Для пересчета V_m на Г_¥ воспользуемся формулой:

Г_¥ = = моль/г.

Удельную поверхность катализатора рассчитывают по уравнению:

S_уд = Г_¥N_AS₀ = 6,64× 10 — 7 × 6,02 × 10 23 ×19,5 × 10 — 20 = 0,078 м 2

Зависимость от .

Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.).

ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала.