Разделы: Математика
Класс: 7
- Проверка практических умений и навыков решения задач на составление уравнения.
- Активизация учебной деятельности учащихся путём общения в динамических парах, когда каждый учит каждого.
- Воспитывать ответственное отношение к учебному труду, развивать логическое мышление, любознательность, умение проверять и оценивать выполненную работу.
Коллективным способом обучения (А. Г. Ривин и В.К. Дьяченко) является такая его организация, при которой обучение осуществляется путём общения в динамических парах, когда каждый учит каждого.
I. Работа начинается с ввода или так называемого “запуска” раздела.
Обобщение и систематизация знаний по теме “ Задачи, решаемые с помощью уравнения”.
1. За 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против течения. Найдите собственную скорость теплохода, если скорость течения реки 2 км/ч.
Пусть собственная скорость теплохода – Х км/ч. Заполним таблицу значений трёх величин.
| Скорость (км/ч) | Время (ч) | Расстояние (км) | |
| По течению | Х + 2 | 9 | 9(Х + 2) |
| Против течения | Х – 2 | 11 | 11(Х – 2) |
На основании условия задачи составим уравнение:
9(Х + 2) = 11(Х – 2), которое имеет единственный корень 20.
Собственная скорость теплохода 20 км/ч.
2. Увеличив среднюю скорость с 250 до300 м/мин, спортсменка стала пробегать дистанцию на 1 мин быстрее. Какова длина дистанции?
Пусть Х мин – время, за которое спортсменка пробегала дистанцию со скоростью 300 м/мин, тогда Х +1 мин – время, за которое спортсменка пробегала дистанцию со скоростью 250 м/мин. Составим уравнение:
250(Х + 1) = 300Х , которое имеет единственный корень 5.Найдём длину дистанции 300Х = 300×5 = 1500 м.
3. В первую бригаду привезли раствора цемента на 50 кг меньше, чем во вторую. Каждый час работы первая бригада расходовала 150 кг раствора, а вторая – 200кг. Через 3 ч работы в первой бригаде осталось раствора в 1,5 раза больше, чем во второй. Сколько раствора привезли в каждую бригаду?
Пусть в первую бригаду привезли Х кг раствора, тогда во вторую – Х + 50 кг. Заполним таблицу значений величин для двух бригад:
| Привезли(кг) | Расход(кг)за 1 час | Время (ч) | Осталось раствора(кг) | |
| 1-я бригада | Х | 150 | 3 | Х – 450 |
| 2-я бригада | Х + 50 | 200 | 3 | Х + 50 – 600 |
По условию задачи в первой бригаде осталось раствора в 1,5 раза больше, чем во второй. Составим уравнение:
Х – 450 = (Х + 50 – 600)×1,5 , имеющее единственный корень 750. 750 кг раствора привезли в первую бригаду, а во вторую привезли 750 + 50 = 800 кг.
4. (Задача Э.Безу) По контракту работникам причитается 48 франков за каждый отработанный день, а за каждый неотработанный день с них вычитается по 12 франков. Через 30 дней выяснилось, что работникам ничего не причитается. Сколько дней они отработали в течение этих 30 дней?
Пусть работники отработали Х дней, тогда они не работали (30 – Х) дней. Составим уравнение:
48Х – 12 (30 – Х) = 0.
Решив это уравнение, получим Х = 6, то есть они отработали 6 дней.
5. Книгу в 296 страниц ученик прочитал за три дня. Во второй день он прочитал на 20% больше, чем в первый, а в третий – на 24 страницы больше, чем во второй. Сколько страниц прочитал ученик в первый день?
Пусть в первый день ученик прочитал Х страниц, тогда во второй день ученик прочитал Х + 0,2Х = 1,2Х страниц, а в третий день прочитал 1,2Х + 24. Составим уравнение:
Х + 1,2Х +1,2Х + 24 = 296. Решив это уравнение, получим Х = 80, то есть ученик прочитал в первый день 80 страниц.
6. На солнышке грелось несколько кошек. У них лап на 10 больше, чем ушей. Сколько кошек грелось на солнышке?
Пусть грелось Х кошек, тогда у этих кошек 2Х ушей и 4Х лап. Составим уравнение:
4Х – 2Х = 10. Решив это уравнение, получим Х = 5,то есть 5 кошек грелось на солнышке.
II. Самостоятельная работа учащихся.
Каждый ученик получает индивидуальную карточку с задачами. Правильность решения проверяет преподаватель, при необходимости он оказывает помощь в решении. После проверки ученику выставляется в оценочный лист плюс или оценка.
Примеры карточек для первой группы:
1. (Старинная задача.) Послан человек из Москвы в Вологду и велено ему проходить во всякий день по 40 вёрст. На следующий день вслед ему был послан другой человек и велено ему проходить по 45 вёрст в день. Через сколько дней второй догонит первого?
2. Чтобы сделать вовремя заказ, артель стеклодувов должна была изготовлять в день по 40 изделий. Однако она изготовляла ежедневно на 20 изделий больше и выполнила заказ на 3 дня раньше срока. Каков был срок выполнения заказа?
Ответ: № 1 – 8 дней, № 2 – 9 дней.
1. Кооператив наметил изготовить партию мужских сорочек за 8 дней. Выпуская в день на 10 сорочек больше, чем предполагалось, он выполнил план за один день до срока. Сколько сорочек в день должен был выпускать кооператив?
2. На ферме 1000 кроликов и кур, у них 3150 ног. Сколько кроликов и сколько кур на ферме?
Ответ: № 1 – 70 сорочек, № 2 – 575 кроликов и 425 кур..
1. Из пункта А вышла грузовая машина со скоростью 60км/ч. Через 2 ч вслед за ней из пункта А вышла легковая машина со скоростью 90 км/ч. На каком расстоянии от пункта А легковая машина догонит грузовую?
2. Чтобы выполнить задание в срок, токарь должен изготавливать по 24 детали в день. Однако он ежедневно перевыполнял норму на 15 деталей и уже за 6дней до срока изготовил 21 деталь сверх плана. Сколько деталей изготовил токарь?
Ответ: № 1 – 360 км, № 2 – 408 деталей.
1. От турбазы до привала туристы шли со скоростью 4,5км/ч, а возвращались на турбазу со скоростью 4км/ч, затратив на обратный путь на 15 мин больше. На каком расстоянии от турбазы был сделан привал?
2. На одном складе было 185 т угля, а на другом – 237 т. Первый склад стал отпускать ежедневно по 15 т угля, а второй – по 18 т. Через сколько дней на втором складе угля будет в полтора раза больше, чем на первом?
Ответ: № 1 – 9 км, № 2 – 9 дней.
Примеры карточек для второй группы:
1. Из пункта А выехал велосипедист. Одновременно вслед за ним из пункта В , отстоящего от пункта А на расстоянии 60 км/ч, выехал мотоциклист. Велосипедист ехал со скоростью 12 км/ч, а мотоциклист – со скоростью 30 км/ч. На каком расстоянии от пункта А мотоциклист догонит велосипедиста?
2. Три бригады изготовили 65 деталей. Первая бригада изготовила на 10 деталей меньше, чем вторая, а третья – 30% того числа деталей, которые изготовили первая и вторая детали вместе. Сколько деталей изготовила каждая бригада?
Ответ: № 1 – 40 км, № 2 – 20, 30, 15 деталей.
1. Расстояние между пристанями М и N равно 162 км. От пристани М отошёл теплоход со скоростью 45 км/ч. Через 45 мин от пристани N навстречу ему отошёл другой теплоход, скорость которого 36 км/ч. Через сколько часов после отправления первого теплохода они встретятся?
2. Бригада рабочих должна была изготовить определённое количество деталей за 20 дней. Однако она ежедневно изготавливала на 70 деталей больше, чем планировалось первоначально. Поэтому уже за 7 дней до срока ей осталось изготовить 140 деталей. Сколько деталей должна была изготовить бригада?
Ответ: № 1 – 2 
1. От пристани А отошел теплоход со скоростью 40 км/ч. Через 1 
2. В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?
Ответ: № 1 – 2 ,5 ч; 150 км, № 2 – 4 овцы и15 кур.
1. Сумму в 74 р. заплатили девятнадцатью монетами по 2 р. и 5 р. Сколько было монет по 2 р.?
2. За 4 ч катер проходит по течению расстояние, в 2,4 раза большее, чем за 2 ч против течения. Какова скорость катера в стоячей воде, если скорость течения 1,5 км/ч?
Ответ: № 1 – 7 монет, № 2 – 16,5 км/ч.
Примеры карточек для третьей группы:
1. Со станции М и N, расстояние между которыми 380 км, одновременно навстречу друг другу вышли два поезда. Скорость поезда, отправившегося со станции N, была больше скорости другого поезда на 5 км/ч. Через 2 ч после отправления поездам оставалось пройти до встречи 30 км. Найдите скорость поездов.
2. В одном резервуаре 380 м³ воды, а в другом 1500 м³. В первый резервуар каждый час поступает 80 м³ воды, а из второго каждый час выкачивают 60 м³. Через сколько часов воды в резервуаре станет поровну?
Ответ: № 1 – 85 и 90км/ч, № 2 – 56 ч.
1. Сумму в 74 р. заплатили девятнадцатью монетами по 2 р. и 5 р. Сколько было монет по 2 р.?
2. Скашивая ежедневно по 60 га вместо 50 га, бригада сумела скосить луг на один день быстрее, чем планировалось. Какова площадь луга?
Ответ: № 1 – 7 монет, № 2 – 300 га.
1. (Старинная задача.) Летели галки, сели на палки: по две сядут – одна палка лишняя, по одной сядут – одна галка лишняя. Сколько было галок и сколько палок?
2. Турист рассчитал, что если он будет идти к железнодорожной станции со скоростью 4км/ч, то опоздает к поезду на полчаса, а если он будет идти со скоростью 5км/ч, то придёт на станцию за 6 мин до отправления поезда. Какое расстояние должен пройти турист?
Ответ: № 1 – 4 галки и 3 палки, № 2 – 12 км.
1. (Задача С.А. Рачинского.) Я дал одному ученику 3 ореха, а всем остальным по 5 . Если бы я всем дал по 4 ореха, у меня осталось бы 15. Сколько было орехов?
2. К числу приписали справа нуль. Число увеличилось на 405. Найдите первое число.
Ответ: № 1 – 83 ореха, № 2 – 45.
Раздел считается введённым в работу, если каждая карточка с заданиями выполнена хотя бы одним учеником.
III. Работа в группах.
Затем работа классного коллектива выглядит так: организуется 3–4 группы по 4 человека (можно до 7 человек). В группе у каждого ученика своя карточка, за которую ученик уже получил плюс или оценку в оценочный лист. Каждый в группе выбирает партнёра, и они меняются карточками. Школьники работают в парах (решают карточку своего партнера полностью), затем пары в группе меняются. Если необходима помощь, то происходит взаимообучение. Если помощь не нужна, то после выполнения задания происходит взаимопроверка и делается отметка в оценочный лист. Потом пары меняются, и процесс продолжается до тех пор, пока каждый ученик не выполнит задания других учеников группы. Затем подводится итог, и выставляется общая оценка.
| №1 | №2 | №3 | №4 | Итоговая оценка |
| Лаптева Алина | 5 | |||
| Борзенков Егор | 3 | |||
| Мартышин Сергей | 4 | |||
| Казакова Виктория | 3 |
По диагонали оценка выставлена учителем. За выполнение карточки № 1оценка выставляется Лаптевой А., № 2 – Борзенковым Е., № 3 – Мартышиным С., № 4 – Казаковой В..
- Конспект урока «Решение задач с помощью уравнений»
- Просмотр содержимого документа «Конспект урока «Решение задач с помощью уравнений»»
- ПЛАН-КОНСПЕКТ УРОКА «Решение задач на проценты с помощью уравнений» план-конспект урока по алгебре (7 класс) по теме
- Скачать:
- Предварительный просмотр:
- Предварительный просмотр:
- Подписи к слайдам:
- По теме: методические разработки, презентации и конспекты
- Математика 7 класс Задачи на части и проценты.
- 🎦 Видео
Видео:РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЙ. §3 алгебра 7 классСкачать

Конспект урока «Решение задач с помощью уравнений»
Данный конспект урока оставлен к учебнику Математика: 7 класс/ А.Г. Мерзляк, В.Б. Полонский, М.С. Якир
Просмотр содержимого документа
«Конспект урока «Решение задач с помощью уравнений»»
Тема урока: Решение задач с помощью уравнений.
Образовательные: формирование знаний, умений и навыков учащихся решать текстовые задачи с помощью уравнений.
Развивающие: развивать умения работать в группе, формировать учебно–познавательные навыки по работе с дополнительным материалом, развивать логическое мышление, внимание;
Воспитательные: воспитывать интерес к математике, старательность, активность, мобильность, взаимопомощь.
Тип урока: усвоение знаний и умений.
Оборудование: карточки, компьютер, проектор, презентация.
Учитель приветствует учеников.
Актуализация опорных знаний.
Учитель раздает каждому учащемуся карточку для проверки уровня усвоения обязательного теоретического материала. В тексте пропущены слова, которые ученики должны вставить. Проверка организована в форме «взаимопроверки» с демонстрацией правильных ответов на экране.
Уравнение вида ax = b, где x – переменная, a и b – некоторые числа, называют линейным уравнением с одной переменной.
Если a ≠ 0, то линейное уравнение имеет единственный корень 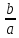
Если a = 0, b = 0, то линейное уравнение имеет бесконечно много корней,
Если a = 0, b ≠ 0, то линейное уравнение не имеет корней.
Чтобы привести уравнение к линейному виду, нужно
Перенести члены с переменными в левую часть уравнения, а другие — в правую, меняя при переносе через знак равенства знаки слагаемых на противоположные;
Привести подобные слагаемые.
Я считаю, что умение решать текстовые задачи необходимо для того, чтобы….
Мотивация учебной деятельности.
Я хочу, чтобы каждый из вас объяснил, почему считает необходимым научиться решать текстовые задачи………
Сегодня на уроке мы должны будем с вами познакомиться с алгоритмом решения задач с помощью линейных уравнений, обращая особое внимание на табличную запись условия. Работая над новой темой, мы проследим вместе с вами, как ранее изученный материал связан с новым, как постепенно происходит расширение и углубление знаний. Одним словом, мы будем объединять отдельные факты в целостный пласт. Я буду вам помогать в процессе систематизации ваших знаний. Мы приступаем к работе.
4. Решение задач с помощью опорных схем.
Коллективное решение задачи на историческую тематику.
Диофант Александрийский — древнегреческий математик.
История сохранила нам мало фактов биографии древнего математика Диофанта. Все, что про него было известно, взято из надписи на его гробнице, составленной в виде математического стихотворения- задачи.
Вот его содержание: «детство Диофанта продолжалось одну шестую часть его жизни, спустя ещё одну двенадцатую у него начала расти борода, он женился спустя ещё одну седьмую, через пять лет у него родился сын, сын прожил половину жизни отца, и отец умер через четыре года после смерти горько оплакиваемого им сына».
Своё основное произведение «Арифметика» Диофант посвятил Дионисию — вероятно, епископу Александрии. До нас дошло шесть первых книг «Арифметики» из тринадцати. Диофант ввёл буквенные обозначения для неизвестного, его квадрата, знака равенства и знака отрицательного числа.
Занимался неопределёнными уравнениями. Ввёл в алгебру буквенную символику.
Большую часть своей жизни Диофант Александрийский посвятил изучению алгебраических уравнений в целых числах. В дошедших до нас книгах «Арифметика» содержатся задачи и решения, в которых Диофант поясняет, как выбрать неизвестное, чтобы решить уравнение вида ax=b или ax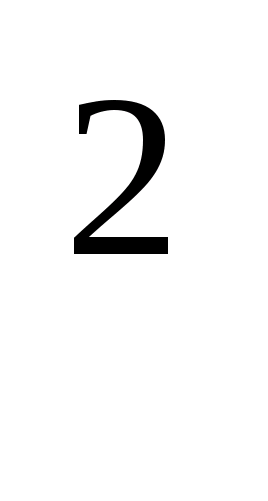
Решив проведенное выше стихотворение-задачу, выясним еще несколько фактов из жизни этого замечательного математика.
Путник! Тут прах похоронен Диофанта. И числа расскажут, о диво, как долго жизнь его длилась
Шестая часть ее прошла счастливым детством
Двенадцатая часть жизни еще прошла-
покрылась пушком его борода
Седьмую в бездетном браке провел Диофант
Прошло пятилетие: он был счастлив рождением прекрасного первенца-сына
Коему судьба только половину жизни прекрасной и светлой дала по сравнению с отцом
И в горе глубоком старик земной жизни конец принял, прожив только года 4 после того, как без сына остался.
Скажи, сколько лет жизни достигнув, принял смерть Диофант?
Решив уравнение, получаем, что х=84. Значит, имеем такие эпизоды биографии Диофанта: женился в 21 год, стал отцом в 38 лет, потерял сына в 80 лет.
Итак, давайте вместе с вами составим алгоритм решения задач с помощью линейных уравнений.
—обозначают некоторое неизвестное число буквой;
—используя условие задачи, составляют уравнение;
-используют полученный результат для истолкования в соответствии с условием задачи.
Формирование умений решать задачи с помощью составления линейных уравнений с одной переменной.
Очень важно при решении любой задачи хорошо разобраться с условием и правильно его записать. Способ записи условия с помощью таблицы очень наглядный.
Купили 2 кг 100 г крупы и высыпали ее в три банки. В первую банку крупы вошло в 3 раза больше, чем во вторую, а в третью банку насыпали 500 г крупы. Сколько крупы насыпали в первую и сколько во вторую банки?
Видео:АЛГЕБРА 7 класс : Решение задач с помощью уравнений | ВидеоурокСкачать

ПЛАН-КОНСПЕКТ УРОКА «Решение задач на проценты с помощью уравнений»
план-конспект урока по алгебре (7 класс) по теме
Урок для обучающихся 7 класса.
Видео:Решение задач с помощью уравнений. Алгебра 7 классСкачать

Скачать:
| Вложение | Размер |
|---|---|
| proekt_uroka_reshenie_zadach_na_procenty_s_pomoshchyu_uravneniy.docx | 37.81 КБ |
| reshenie_zadach_na_procenty_s_pomoshchyu_uravneniy.ppt | 899.5 КБ |
Видео:Урок по теме РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ 7 КЛАСССкачать

Предварительный просмотр:
ПЛАН-КОНСПЕКТ УРОКА
«Решение задач на проценты с помощью уравнений»
Якименко Евгения Александровна
МОУ СОШ №6 г. Богородск Нижегородской области
Тема «Решение задач на проценты с помощью уравнений»
Гл.2 «Уравнения с одним неизвестным» ( урок 5 в данной теме)
Ш.А. Алимов, Ю.М. Колягин и др. «Алгебра 7», М.: Просвещение, 2009 г.
- Цель и задачи урока
Цель: выявить задачи трех видов на проценты и найти способы их решения, закрепить умение решать основные задачи на проценты; создать и исследовать математическую модель.
познакомить учащихся с понятиями «скидка», «распродажа», «бюджет», «тарифы», «пеня»;
исследовать обобщенную схему решения, спрогнозировать конкретную ситуацию и исследовать ее.
сформировать умение применять знания процентов в жизненных ситуациях.
- Тип урока — комбинированный
- Формы работы учащихся — фронтальная, индивидуальная, самостоятельная работа в парах.
- Необходимое техническое оборудованиекомпьютер для учителя с выходом в Интернет, мультимедиа-проектор, мультимедийный экран, 12 компьютеров, авторская электронная презентация с необходимыми упражнениями и изображениями.
- Структура и ход урока
1) Организационный момент.
2) Сообщение цели урока.
3)Устная работа (актуализация прежних знаний).
4) Изучение нового материала.
5) Первичное закрепление.
6) Подведение итогов.
СТРУКТУРА И ХОД УРОКА
Название используемых ЭОР
(с указанием порядкового номера из Таблицы 2)
(с указанием действий с ЭОР, например, демонстрация)
Проверка явки на урок, отметка в журнале отсутствующих
Ребята настраиваются на работу
Сообщение цели урока
— Сегодня на уроке, ребята вы, вместе со мной вспомните решение задач на проценты, а также вы исследуете еще один способ решения задач на проценты
(актуализация прежних знаний).
— Выполните устно задания, представленные вашему вниманию на экране:
1. Представьте данные десятичные дроби в процентах:
0,5 0,24 0,867 0,032 1,3 0,0081
0,01 154 3,2 0,7 10 15
Проговаривают устно и смотрят правильный ответ на доске
50% 24% 86,7% 3,2% 130% 0,81%
1% 15400% 320% 70% 1000% 1500%
- Представьте проценты десятичными дробями:
2% 12,5% 2,67% 0,06% 32,8%
1000% 510% 0,5% 213% 0,1%
0,02 0,125 0,0267 0,0006 0,328
10 5,1 0,005 2,13 0,001
— Основные понятия, связанные с процентами:
- Нахождение процентов данного числа.
Решение задачи записываем в тетради.
30% от 60 составляет?
Чтобы найти а % от в , надо в∙0,01а.
2. Нахождение числа по его процентам.
3% числа х составляют 150.
Если известно, что а% числа х равно в , то х=в:0,01а
3.Нахождение процентного отношения чисел.
Сколько процентов составляет 150 от 600?
Чтобы найти процентное отношение чисел, надо отношение этих чисел умножить на 100%. 100%
— Прослушивание информации и выполнение тестового задания
— Решение основных задач на проценты.
На сколько процентов надо увеличить число 90, чтобы получить 120?
Цену товара снизили на 30%, затем новую цену повысили на 30%. Как изменилась цена товара?
Пусть первоначальная цена товара а, тогда:
а-0,3а=0,7а – цена товара после снижения,
0,7а+0,7а 0,3=0,91а – новая цена.
1,00-0,91=0,09 или 9%
Ответ: цена снизилась на 9%
Почему нельзя сказать, что цена товара не изменилась?
Так как повышение цены товара на 30% произошло от измененной цены, а не первоначальной.
В повседневной жизни все мы являемся покупателями, оплачиваем коммунальные услуги, иногда случается, что приходится платить штрафы, а также производим некоторые банковские операции, делаем маринады для консервирования. Поэтому сегодня на уроке попробуем решить все эти проблемы. В этом нам помогут знания по математике.
Зонт стоил 360 рублей. В ноябре цена зонта была снижена на 15%, а в декабре еще на 10%. Какой стала стоимость зонта в декабре?
- 100-15=85%
- 360∙0,85=306(р)- стоимость зонта в ноябре.
- 100-10=90%
- 306∙0,9=275,4(р)-стоимость зонта в декабре.
Ответ: 275 руб.40 коп.
Дополнительный вопрос: На сколько процентов по отношению к первоначальной цене подешевел зонт?
При приеме на работу директор предприятия предлагает зарплату 4200 р. Какую сумму получит рабочий после удержания налога на доходы физических лиц?
При начислении налога на доходы физических лиц нужно учитывать стандартный вычет 400 р., налог 13% берется от оставшейся суммы.
В газете сообщается, что с 10 июня согласно новым тарифам стоимость отправления почтовой открытки составит 3 р.15к. вместо 2 р.75 к. Соответствует ли рост цен на услуги почтовой связи росту цен на товары в этом году, который составляет 14,5%.
Дополнительный вопрос. Сколько будет стоить отправка заказного письма, если эта услуга сейчас оценивается в 5 р. 50 к?
Занятия ребенка в музыкальной школе родители оплачивают в сбербанке, внося ежемесячно 250 р. Оплата должна производиться до 15 числа каждого месяца, после чего за каждый просроченный день начисляется пеня в размере 4% от суммы оплаты занятий за один месяц. Сколько придется заплатить родителям, если они просрочат оплату на неделю?
- 0,04∙250=10 (р.) — штраф
- 250+10=260 (р.) — оплата, если просрочат 1 день
- 250+10∙7=320 (р.) – придется заплатить родителям
Ответ: 320 рублей.
Гимнастика для глаз.
Изучение нового материала
Сколько граммов воды надо добавить к 50 г раствора, содержащего 8% соли, чтобы получить 5% раствор?
Поможет нам решить эту задачу уравнение. Что называют уравнением?
Равенство, содержащее неизвестное, обозначенное буквой.
Значит, мы должны составить равенство, в котором одна из неизвестных величин обозначена буквой. Какую из величин обозначим буквой?
Пусть хг – количество воды, которое надо добавить,
— Уравнение – это равенство, поэтому теперь мы должны составить равенство, в котором будет участвовать х и другие величины. Для этого нам потребуется выразить и другие неизвестные в задаче величины через х.
(50+х)г – новое количество раствора
50∙0,08г – количество соли в исходном растворе
0,05∙(50+х) г – количество соли в новом растворе
— Итак, все неизвестные величины мы выразили через данные и через х. Все ли данные в условии задачи величины мы использовали?
— Как записать это отношение в виде равенства?
— Итак, мы получили уравнение, которое является математической моделью для данной задачи. Теперь мы создали математическую модель задачи. Каким должен быть следующий шаг в решении задачи?
— Как исследовать полученную модель?
— Давайте устно проведем анализ найденной величины.
Проводится анализ задачи.
№2 Задача на проценты
— Предлагаю вам провести проверку усвоенных знаний, для этого вам нужно пройти к компьютерам и выполнить задания, предложенные в модуле
— Ребята выполняют тест на компьютере с самопроверкой, те ребята, которые выполнили раньше могут подойти и оказать помощь нуждающимся.
— На следующем уроке мы продолжим учиться решать задачи с помощью уравнений, а дома попробуйте составить сюжетную задачу, которую можно решить с помощью уравнения.
Можно приготовить презентацию.
— Запись домашнего задания в дневник.
Оцените свое умение выполнять каждое из указанных действий. (Раздаются карточки.)
Напротив каждого действия поставьте
Нахождение процентов от данного числа
Нахождение числа по его процентам.
Нахождение процентного отношения чисел.
Решение основных задач на проценты.
Решение сюжетных задач.
Составление математической модели.
Учащиеся индивидуально оценивают свое умение выполнять перечисленные действия. Результаты этой работы будут учтены при составлении системы упражнений для актуализации знаний на следующем уроке. Учащиеся также оценивают собственный вклад в совместно полученные результаты деятельности на уроке, отражая собственное эмоциональное состояние.
Приложение к плану-конспекту урока
«Решение задач на проценты с помощью уравнений»
ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ НА ДАННОМ УРОКЕ ЭОР
Тип, вид ресурса
Форма предъявления информации (иллюстрация, презентация, видеофрагменты, тест, модель и т.д.)
Гиперссылка на ресурс, обеспечивающий доступ к ЭОР
OMS Module file
OMS Module file
Решение задач на проценты
OMS Module file
Предварительный просмотр:
Видео:Решение задач с помощью уравнений. Алгебра, 7 классСкачать

Подписи к слайдам:
«Решение задач на проценты с помощью уравнений» 7 класс Учитель Якименко Е.А. Богородск 2011-2012 учебный год Муниципальное образовательное учреждение средняя общеобразовательная школа № 6
Содержание Представьте десятичные дроби в процентах. Представьте проценты десятичными дробями. Основные понятия, связанные с процентами . Распродажа. Бюджет. Зарплата. Тарифы. Штрафы. Растворы. Основные этапы решения задачи Домашнее задание. Рефлексия
Представьте данные десятичные дроби в процентах: 0,5 0,24 0,867 0,032 1,3 0,0081 0,01 154 3,2 0,7 10 15 50% 50% 50% 50% 50% 50% 50% 3,2% 86,7% 130% 0,81% 1% 15400% 24% 320% 70% 1000% 1500%
Представьте проценты десятичными дробями: 2% 12,5% 2,67% 0,06% 32,8% 1000% 510% 0,5% 213% 0,1% 0,02 0,125 0,0267 0,0006 0,328 5,1 10 0,005 2,13 0,001
Заполни таблицу 18% р% 18 100 р 100 0,01р 0,18
1. Нахождение процентов данного числа. Чтобы найти a% от b , надо b · 0,01a 30% от 60 составляет ? x = 150 : 0,03 x = 5000 2. Нахождение числа по его процентам. Если известно, что a% от x равно b , то x = b : 0,01a 3% от числа x составляют 150 ? 60 · 0,3 = 18 Основные понятия, связанные с процентами
3. Нахождение процентного отношения чисел Чтобы найти процентного отношения чисел, надо отношение этих чисел умножить на 100%. Сколько процентов составляет число 150 от 600 ? Основные понятия, связанные с процентами Слайд 17 Авторская презентация
Модуль 1 Повторим еще раз Модуль1. oms
Решение основных задач на проценты. На сколько процентов надо увеличить число 90, чтобы получить 120? 120 – 90 = 30 30: 90 = ∙ 100% = 33 Ответ: 33
Решение основных задач на проценты. Цену товара снизили на 30%, затем новую цену повысили на 30%. Как изменилась цена товара? Пусть первоначальная цена товара а, тогда: а-0,3а=0,7а – цена товара после снижения, 0,7а+0,7а 0,3=0,91а – новая цена. 1,00-0,91=0,09 или 9% Ответ: цена снизилась на 9%
Распродажа. Зонт стоил 360 рублей. В ноябре цена зонта была снижена на 15%, а в декабре еще на 10%. Какой стала стоимость зонта в декабре? 100-15=85% 360∙0,85=306( р)- стоимость зонта в ноябре. 100-10=90% 306∙0,9=275,4(р)-стоимость зонта в декабре. Ответ: 275 руб.40 коп.
Бюджет. Зарплата. При приеме на работу директор предприятия предлагает зарплату 4200 р. Какую сумму получит рабочий после удержания налога на доходы физических лиц?
При начислении налога на доходы физических лиц нужно учитывать стандартный вычет 400 р., налог 13% берется от оставшейся суммы. (4200-400)∙0,13=494 (р.)-налог 4200-494=3706 (р.) Ответ: 3706 р.
Тарифы. В газете сообщается, что с 10 июня согласно новым тарифам стоимость отправления почтовой открытки составит 3 р.15к. вместо 2 р.75 к. Соответствует ли рост цен на услуги почтовой связи росту цен на товары в этом году, который составляет 14,5%. 3,15-2,75=0,4(р)-разность тарифов 0,4:3,15=0,14545… 0,14545=14,5% Ответ: соответствует
Штрафы. Занятия ребенка в музыкальной школе родители оплачивают в сбербанке, внося ежемесячно 250 р. Оплата должна производиться до 15 числа каждого месяца, после чего за каждый просроченный день начисляется пеня в размере 4% от суммы оплаты занятий за один месяц. Сколько придется заплатить родителям, если они просрочат оплату на неделю? 0,04∙250=10 (р.) — штраф 250+10=260 (р.) — оплата, если просрочат 1 день 250+10∙7=320 (р.) – придется заплатить родителям Ответ: 320 рублей.
Растворы. Сколько граммов воды надо добавить к 50 г раствора, содержащего 8% соли, чтобы получить 5% раствор?
Приготовление маринада Пусть х г – количество воды, которое надо добавить, (50+х )г – новое количество раствора 50∙0,08 г – количество соли в исходном растворе 0,05∙(50+х) г – количество соли в новом растворе
Решение уравнения Составим уравнение: 50∙0,08 = 0,05∙(50+х), 50∙8 = 5∙(50+х), 80 = 50+х, х = 30 Ответ: 30 г.
Основные этапы решения задачи 1. Проанализировать условие задачи, составить краткую запись. 2. Обозначить неизвестную величину буквой х. 3. Выразить все неизвестные величины через данные и х. 4. Составить уравнение. 5. Решить уравнение. 6. Найти искомую величину. 7. Проверить результат по смыслу задачи. 8. Записать ответ.
Самостоятельная работа Решите задачу с помощью уравнения
Домашнее задание Составить сюжетную задачу, которую можно решить с помощью уравнения. Решить эту задачу. Создать презентацию
Рефлексия Напротив каждого действия поставьте «+» — нет затруднений; «+-» — необходима тренировка; «-» — испытываю затруднения. Нахождение процентов от данного числа Нахождение числа по его процентам. Нахождение процентного отношения чисел. Решение основных задач на проценты. Решение сюжетных задач. Составление математической модели. Исследование модели.
Видео:Решение задач с помощью уравненийСкачать

По теме: методические разработки, презентации и конспекты
Интегрированный урок физики и математики Тема урока: Решение физических задач с помощью линейных уравнений
Урок на данную тему проводился в рамках открытого методического дня школы. На уроке присутствовали учителя не только школы и города, но школ Республики Хакасия. Всего на уроке было гостей 16 человек. .
ПЛАН – КОНСПЕКТ УРОКА «Урок – решение задач прямолинейного движения тел».
ПЛАН – КОНСПЕКТ УРОКА «Урок – решение задач прямолинейного движения тел».Цель урока: Формировать систему представлений о механическом движении объекта и системы объектов.Задачи: Научить а)анализ.
ПЛАН – КОНСПЕКТ УРОКА «Урок – решение задач прямолинейного движения тел».
ПЛАН – КОНСПЕКТ УРОКА «Урок – решение задач прямолинейного движения тел».Цель урока: Формировать систему представлений о механическом движении объекта и системы объектов.Задачи: Научить а)анализ.
План -конспект урока на тему «Задачи на проценты»
План урока с подробным описанием всех этапов.
ПЛАН-КОНСПЕКТ открытого урока Решение задач по теме «треугольники»
ПЛАН-КОНСПЕКТ УРОКА Решение задач по теме «треугольники» 7 класс.Урок-закрепление.
Конспект урока «Решение текстовых задач с помощью квадратных уравнений», 8 класс, Алимов Ш.А., Колягин Ю.М.
Конспект урока по теме «Решение текстовых задач с помощью квадратных уравнений»Обучающие цели: Обеспечить усвоение умения решать алгебраические и геометрические задачи с помощью квадратных.
Открытый урок » решение экономических задач на проценты»
Решение задач экономического характера на проценты-одна из тем,которая интересна от 5 до 11 класса.Тем более для нашего Пушкинского лицея экономики политики и права.
Видео:МЕРЗЛЯК-7. РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ. ПАРАГРАФ-3. ЧАСТЬ-1Скачать

Математика 7 класс Задачи на части и проценты.
1 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СПЕЦИАЛИЗИРОВАННЫЙ УЧЕБНО-НАУЧНЫЙ ЦЕНТР Математика 7 класс Задачи на части и проценты. Новосибирск
2 Задачи на части и проценты. Дробные числа удобно сравнивать и выполнять арифметические действия с ними, если они выражены в одинаковых долях. На практике удобными оказались сотые доли. Сотую часть центнера называют килограммом, сотую часть метра — сантиметром, сотую часть гектара аром или соткой, и т.д.. Сотую часть любой величины или числа принято называть процентом. Процентом называют сотую часть числа. Слово «процент» происходит от латинских слов «pro centum», что означает «с сотни». Раньше процентами называли деньги, которые должник платил дополнительно за каждую занятую сотню рублей. Вместо слова «процент» пишут значок «%». С помощью этого знака 1 можно записать: 1 % или 1 % 0, Выражение процентов десятичной дробью. Если необходимо записать проценты в виде десятичной дроби, то удобно применить следующее правило: знак «%» заменяет множитель 0, 01. Например, 7 % 7 0,01 0, 07, 300 % 300 0,01 3, 0,2% 0,2 0,01 0,002, 23 % 23 0,01 0,23. Выражение числа в процентах. Так как единица содержит сто сотых долей, то %. А так как любое число можно представить в виде произведения единицы на это число, то значит, любое число можно выразить в процентах. Например, % 500%, 0,33 0,33 1 0,33 100% 33%, 1,25 1,25 1 1,25 100% 125%, % 12,5%. 2
3 Основные типы задач на проценты. 1. Нахождение процентов от данного числа. Задача 1. Из 33 учащихся класса 25% учатся на «отлично» и 50% на «хорошо». Сколько учащихся класса обучается на «отлично» и «хорошо» в отдельности? Так как 25%=0,25, 50% = 0,5, то 36 0,25 9(уч) учатся на «отлично», 36 0,5 18 (уч) учатся на «хорошо». Ответ: 9уч., 18уч.. Замечание. При решении задач полезно использовать следующий 50 1 факт: 50% — это половина величины ( 50 % ), % — это четверть величины ( 25 % ), % — это пятая часть величины ( 20 % ) Нахождение числа по его процентам. Задача 2. 60м составляют 20% той высоты, на которой жаворонка уже не видно, а 48м составляют 8% высоты, с которой ещё слышно его пение. Определите ту и другую высоты? Удобно решить эту задачу с помощью пропорции. 60м сост. 20%, x м сост. 100% x Значит, на высоте 300метров жаворонка уже не видно. 48м сост. 8%, y м сост. 100% y Следовательно, на высоте 600метров ещё слышно его пение. Ответ: 300м, 600м. 3
4 3. Нахождение процентного отношения двух чисел. Задача 3. В новогоднюю коробку положили 16 конфет «Маска», 24 конфеты «Ромашка» и 40 ирисок «Золотой ключик». Определите процентное содержание конфет каждого сорта, содержащихся в коробке. Всего конфет =80. Определим процентное содержание конфет каждого сорта, содержащихся в коробке % 20% — приходится на конфеты «Маска», % 30% — приходится на конфеты «Ромашка», % 50% — приходится на конфеты «Золотой ключик». 80 Ответ: 20%, 30%, 50%. Следовательно, чтобы найти процентное отношение двух чисел, нужно найти отношение этих чисел и выразить его в процентах, т.е. умножить это отношение на 100%. Решим несколько несложных задач на проценты. Задача 4. Черные лебеди составляют 40% от общего числа белых и черных лебедей, живущих в заповеднике. Сколько черных лебедей живет в заповеднике, если число белых лебедей на 21 больше числа черных? Ясно, что на долю белых лебедей приходится 60%. Так как по условию задачи число белых лебедей на 21 больше числа черных, то в процентах эта разница выражается числом: 60%-40%=20%. Итак, на 20% приходится 21 лебедь, тогда очевидно, что на 40% приходится вдвое больше лебедей, т.е. 42. Следовательно, в заповеднике живет 42 черных лебедя. Ответ: 42 черных лебедя. 4
5 Задача 5. Двое рабочих изготовляли одинаковые детали. Один из них недовыполнил норму на 10%, а другой перевыполнил норму на 20%, сделав на 45 деталей больше, чем первый. Сколько деталей составляет норму? Сколько деталей изготовил каждый рабочий? Так как первый рабочий недовыполнил норму на 10%, значит, он выполнил 90% нормы, тогда второй, перевыполнив норму на 20%, выполнил 120% нормы. Второй рабочий выполнил на 30% больше первого, поэтому 45 деталей составляют не 20%, а 30%. 1) 45:30 = 1,5(детали) составляет 1%, 2) 1, (деталей) изготовил первый рабочий, 3) 1, (деталей) изготовил второй рабочий, 4) 1, (деталей) норма. Ответ: 150 деталей, 135 деталей, 180 деталей. Задача 6. 45% всей земли совхоза занято лугом, 60% остатка пашней, а остальная часть лесом. Найдите площадь всей земли совхоза и площадь леса, если известно, что площадь леса меньше площади пахотной земли на 770га. 1. Разберемся сначала с остатком земли (вся земля без луга). Ясно, что если на пашню приходится 60%, то на лес остается 100%-60%=40%. Значит, площадь леса меньше площади пашни на 60%-40%=20%, что составляет 770га. С помощью пропорции определим площадь остатка земли. 770га сост.20%, x га сост. 100%, x га — площадь остатка земли. 2. Теперь определим площадь всей земли совхоза. Остаток составляет 100%-45%=55% всей земли (заметим, что в этом случае за 100% принимается площадь всей земли). С помощью пропорции определим площадь всей земли. 3850га сост.55%, 5
6 y га сост. 100%, y Итак, 7000га площадь всей земли совхоза. Так как лес составляет 40% от пашни, то найдем 40% от 3850га: 0, (га) занято лесом. Проверка. 1) , (га) площадь луга, 2) (га) остаток земли, 3) , (га) пашня, 4) , (га) лес, 5) (га). Действительно, разница площадей отведенных под пашню и лес равна 770га, что соответствует условию задачи. Задача решена верна. Ответ: 7000га, 1540га. Решить задачу разными способами это гораздо ценнее, нежели решить несколько аналогичных (однотипных) задач. На примере следующей задачи рассмотрим различные подходы к анализу задачи и её решению. Самый рациональный способ решения этой задачи легко выбрать из предложенных. Задача 7. Саша прочитал в первый день 25% книги, во второй день — 2 книги, после чего ему осталось прочитать 17 страниц. Сколько 3 страниц в книге? 1 способ. Легко видеть, что если во второй день прочитано 3 2 книги, то 25% книги и 17 страниц вместе составляют 3 1 всей книги. Значит, количество страниц в книге в 3 раза больше, то есть равно сумме 75% книги+51страница. Эта запись говорит о том, что 51 страница составляет 25% книги, т.е. её четвертую часть. Следовательно, в книге в 4 раза больше страниц, т.е (страницы). 6
7 2 способ. Решим задачу алгебраическим способом (через уравнение). Пусть в книге x страниц, тогда 1 x страниц прочитано Сашей в 4 первый день и 2 x страниц во второй день. 3 Так как осталось прочесть 17 страниц, то имеем уравнение: 1 2 x x 17 x, решением которого является x Значит, в книге 204 страницы. 3 способ. 25% книги составляет 4 1 её часть. Узнаем, какую часть книги прочитал Саша за 2 дня: (книги). 12 Значит, на оставшуюся 12 1 часть книги приходится 17 страниц. Очевидно, что вся книга имеет (страниц). Ответ: 204 страницы. На примере решения следующей задачи напомним способ решения задач на части. Задача 8. Для изготовления раствора берут известь и песок в отношении 3 : 5. Сколько килограммов извести и песка в отдельности надо взять для приготовления 640кг раствора? 1 способ (арифметический). 1) = 8 (частей) содержит смесь, 2) 640 : 8 = 80 (кг) масса одной части, 3) (кг) масса извести в смеси, 4) (кг) масса песка в смеси. Получили, что для приготовления 640кг раствора необходимо взять 240кг извести и 400кг песка. 2 способ (алгебраический). Пусть x кг масса одной части смеси. Тогда на долю извести приходится 3x кг, на долю песка — 5x кг. Согласно условию задачи 7
8 имеем уравнение: 3x 5x 640, откуда x 80. Найдя массу одной части, определим массу извести и массу песка в смеси (кг) масса извести в смеси, (кг) масса песка в смеси. Ответ: 240кг, 400кг. Рассмотрим решение простейшей задачи на сплав металлов, которая тоже относится к задачам на части. Задача 9. Сплавили золото и серебро в отношении 3 : 7, золота взяли 0,36кг. Чему равна масса всего сплава? Определите процентное отношение золота в сплаве. В сплаве содержится 0,36кг золота, что составляет 3 части сплава. Поэтому 0,36:3=0,12(кг) масса одной части. Весь сплав состоит из 10 частей (3ч+7ч), значит, 0, , 2 (кг) масса всего сплава. Определим процентное содержание золота в сплаве: 0,36 0,3 100% 100% 30%. 1,2 1 Процентное содержание золота в сплаве можно определить другим способом, зная отношение 3 : 7 его составляющих компонентов: 3 100% 0,3 100% 30%. 10 Ответ: 1,2кг; 30%. Задача 10. Велотрасса состоит из трех участков: равнинного, подъема в гору и дороги под уклон. Длина участка под уклон составляет 75% 3 от длины подъема в гору, а равнинный участок в 2 раза длиннее, 5 чем участок трассы под уклон. Найдите длину каждого участка, если длина всей велотрассы 74км? Обозначим длину участка в гору через x км, тогда длина участка под 3 уклон равна 0,75 x км и длина равнинного участка — 2 0,75x км. 5 8
9 Длина всей велотрассы 74км, что позволяет составит уравнение: 3 x 0,75x 2 0,75x 74, решением которого является x Итак, 20км длина участка в гору, 0,75 20=15(км) длина участка под уклон, 3 2 0, (км) длина равнинного участка. 5 Ответ: 20км, 15км, 39км. Задача 11. Букинистический магазин, купив две книги на сумму 360руб, продал их, получив 25% прибыли. По какой цене была продана каждая книга, если на первую книгу была наценка 50%, а на вторую 12,5%? 25% прибыли означает, что новая сумма составляет 125% от первоначальной суммы 360 рублей. С помощью пропорции определим, что выручил букинистический магазин от продажи этих книг по новой цене. 360руб сост. 100%, x руб сост. 125%, x Значит, обе книги вместе проданы за 450рублей. Пусть a рублей стоила первая книга, а b рублей стоила вторая книга первоначально. Согласно условию задачи оформим таблицу. перв. цена наценка итоговая цена 1 книга a руб 50% 0,5 a руб a 0,5 a 1, 5a руб 2 книга b руб 12,5% 0,125 b руб b 0,125 b 1, 125b руб Зная, что первоначальная стоимость обеих книг равна 360руб, а после наценки они проданы за 450руб, составим и решим систему a b 360, уравнений. 1,5a 1,125b 450. Решим систему способом сложения. 9
10 Домножив обе части первого уравнения на (-1,5), сложим полученное уравнение со вторым уравнением системы почленно, получим: 0,375b 90. Откуда b 240. Из первого уравнения найдем значение второй переменной: a 120. Мы определили первоначальную стоимость книг: 120руб первая книга, 240руб вторая. После наценки книги были проданы по следующей цене: 1, (руб.) первая, 1, (руб.) вторая. Ответ: 180руб, 270руб. Рассмотрим довольно подробно решение следующей задачи с помощью табличного метода. Не сомневаемся, что овладение этим методом позволит логически последовательно и достаточно легко справляться даже со сложными задачами на смеси и сплавы. Заметим, что в задачах такого типа удобно проценты записывать десятичной дробью. Задача 12. Подсолнух содержит 25% шелухи, а обработанный 5% шелухи. Сколько обработанной массы получится из 190кг подсолнуха? Анализ задачи. 1 этап. Вносим в таблицу все исходные данные и обозначаем искомую величину. Обозначим через x кг количество обработанной массы, полученной из 190кг подсолнуха (сырья). Необходимо понимать, что обработанный подсолнух все равно содержит шелуху, но, естественно, в гораздо меньшем количестве, 25 1 нежели сырье (в сырье — 25% часть всего подсолнуха, а в обработанном — 5% часть всей обработанной массы) подсолнух обработ. масса общая масса 190кг x кг чистые семечки шелуха 25% 5% 10
11 2 этап. Заполняем все остальные ячейки таблицы согласно условию задачи. Таким образом, мы получаем всю информацию о каждом составляющем компоненте смеси как в процентах (или долевом соотношении), так и в количественном соотношении (в килограммах). В 190кг подсолнуха (сырья) содержится: 25% шелухи, что составляет 0, кг = 47,5кг, 75% чистых семечек, что составляет 0,75 190кг = 142,5кг. В обработанной массе содержится: 5% шелухи, что составляет 0,05 x кг, 95% чистых семечек, что составляет 0,95 x кг. подсолнух обработ. масса общая масса 190кг x кг чистые семечки 75% 0,75 190кг 95% 0,95 x кг шелуха 25% 0, кг 5% 0,05 x кг Замечание. В таблицу обязательно вписываются единицы измерения величин, так как иначе это может привести к грубым ошибкам при составлении уравнения или системы уравнений. 3 этап. С помощью заполненной таблицы составляется уравнение (если введена одна переменная) или система уравнений (в случае необходимости введения двух переменных). Очевидно, что количество чистых семечек, полученных из подсолнуха (сырья) равно количеству чистых семечек в обработанной массе, поэтому получаем уравнение: 0,95x 0,75 190, откуда x 150. Следовательно, 150кг количество обработанной массы. Проверка. В 150кг обработанной массы содержится 95% чистых семечек, т.е ,95 142,5 кг. Это же количество чистых семечек содержится и в 190кг сырья. 11
12 Определим процентное содержание чистых семечек в этом количестве 142,5 сырья: 100% 75%. Значит, на шелуху остается 100% %=25%, что соответствует условию задачи. Вывод: задача решена верно. Ответ: 150кг. Задача 13. Имеются два сплава, в одном из которых содержится 20%, а в другом 30% олова. Сколько нужно взять первого и второго сплавов, чтобы получить 10кг нового сплава, содержащего 27% олова? 1 способ. Решим задачу алгебраическим способом (с помощью системы уравнений). Заполним таблицу согласно условию задачи. 1 сплав 2 сплав новый сплав общая масса x кг y кг 10 кг олово 20% 0,2x кг 30% 0,3y кг 27% 0,27 10 кг Пусть x кг масса первого сплава, в котором содержится 0,2x кг олова, а y кг масса второго сплава, в котором содержится 0,3y кг олова. Т.к. в смеси содержится олова 0,27 10 кг, то имеем уравнение: 0,2x 0,3y 0, (1) Кроме этого, третий сплав это смесь первого и второго сплавов, поэтому имеем второе уравнение: x y 10. Получаем систему уравнений: 0,2x 0,3y 2,7, x y 10. Умножим обе части уравнения (1) на 10, тогда получим систему: 2x 3y 27, решением которой является x 3, y 7. x y 10, 12
13 II способ. Решим задачу алгебраическим способом (с помощью уравнения). 1 сплав 2 сплав новый сплав общая x кг ( 10 x ) кг 10 кг масса олово 20% 0,2x кг 30% 0,3 10 x кг 27% 0,27 10 кг Т.к. 10 кг это смесь первого и второго сплавов, то необходимо взять x кг первого сплава и ( 10 x ) кг второго сплава. Рассуждая аналогично тому, как это сделано при первом способе решения, получим уравнение: 0,2x 0,3 10 x 2, 7, решением которого является x 3. Итак, было взято 3 кг первого сплава и 7 кг второго. Проверка: 1) 0,2 3 0, 6 (кг) масса олова в первом сплаве. 2) 0,3 7 2, 1 (кг) масса олова во втором сплаве. 3) 0,6 2,1 2, 7 (кг) масса олова в их смеси. 2,7 4) % 27%. Процентное содержание олова в смеси составляет 27%, что соответствует условию задачи. Ответ: 3 кг, 7 кг. Задача 14. Смешали некоторое количество 30%-го раствора соляной кислоты с некоторым количеством 10%-го раствора и получили 600г 15%-го раствора. Сколько граммов каждого раствора было взято? Решим задачу табличным методом. Для решения задачи достаточно заполнить только первую часть таблицы. общая масса кислота (чистая) вода 1 раствор 2 раствор смесь x г ( 600 x ) г 600 г 30% 0,3x г 10% 0,1 600 x г 15% 0, г 13
14 Пусть смешали x г 30%-го раствора с ( 600 x ) г 10%-го раствора. Чистой (безводной) соляной кислоты содержится в первом растворе 0,3x г, во втором растворе 0,1 600 x г, а в смеси этих растворов содержится 0, г. Ясно, что масса чистой кислоты в смеси является суммарной массой кислоты в первом и втором растворах, поэтому имеем уравнение: 0,3x 0,1 600 x 0, (1) или 0,3x 0,1 600 x 90, решением которого является x 150. Итак, было взято 150 г первого раствора и 450 г второго раствора. Замечание: Если заполнить все ячейки таблицы до конца, то получим следующую таблицу: 1 раствор 2 раствор смесь общая x г ( 600 x ) г 600 г масса кислота 30% 0,3x г 10% 0,1 600 x г 15% 0, (чистая) г вода 70% 0,7x г 90% 0,9 600 x г 85% 0, г Тогда можно составить другое уравнение относительно переменной x (из строки, соответствующей содержанию воды): 0,7x 0,9 600 x 0, (2) Самостоятельно проверьте, что корень уравнения (2) совпадет с корнем уравнения (1). Ответ: 150 г, 450 г. Задача 15. Если число волков в тамбовском лесу увеличится на 1000 голов, а количество зайцев возрастет на 10%, то на каждого зайца будет приходиться ровно по одному волку. Если поголовье волков в тамбовском лесу сократится на 10%, а зайцев станет на 955 меньше, то на каждого зайца будет ровно по два волка. Сколько волков и сколько зайцев в тамбовском лесу? Решим задачу алгебраическим способом с помощью системы линейных уравнений. Заметим, что прежде, чем оформлять решение этой задачи, удобнее сначала собрать результаты анализа в таблицу. 14
15 было I изменение станет вывод волков x x 1000 Зайцев и волков зайцев y +10% 0,1 y y 0, 1y станет поровну Пусть в тамбовском лесу x волков и y зайцев. В результате первого изменения имеем (x 1000) волков и 1,1 y зайцев. Т.к. на каждого зайца будет приходиться ровно по одному волку, то это означает, что количество волков равно количеству зайцев. Имеем первое уравнение: x , 1y. было II изменение станет вывод волков x -10% 0,1x x 0, 1x Зайцев зайцев y -955 y станет вдвое меньше, чем волков В результате второго изменения поголовья в тамбовском лесу станет 0,9x волков и ( y 955) зайцев. По условию задачи на каждого зайца теперь будет приходиться ровно по два волка. Это значит, что количество волков вдвое больше количества зайцев, поэтому имеем второе уравнение: 0,9x 2 ( y 955). x ,1 y, Решаем систему уравнений способом 0,9x 2 ( y 955) алгебраического сложения. Умножив первое уравнение системы на 0, 9 и сложив почленно со вторым уравнением системы, получим уравнение: ,01y, решением которого является y Из первого уравнения данной системы находим соответствующее значение второй переменной x 100. Итак, в тамбовском лесу было 100 волков и 1000 зайцев. Ответ: 100 волков и 1000 зайцев. Задача 16. В магазине «Мойдодыр» в продаже имеются стиральные порошки в пачках трех сортов: обычный, необычный и превосходный. Сначала количественное соотношение по сортам было 3 : 4 : 6. В результате продаж и поставок со склада это соотношение изменилось и стало 2 : 5 : 8. Известно, что число пачек необычного порошка
16 возросло на 55, а обычного порошка уменьшилось на 10%. Сколько всего пачек порошка стало в магазине? Заполним таблицу согласно условию задачи. было изменение стало обычный 3 x пачек -10% 0,1 3x 2 y пачек пачек необычный 4 x пачек +55 пачек 5 y пачек превосходный 6 x пачек 8 y пачек всего 13 x пачек 15 y пачек Пусть сначала одна часть составляла x пачек. Тогда обычного порошка было 3 x пачек, необычного 4 x пачек и превосходного 6 x пачек. В результате продаж и поставок со склада количественное соотношение порошков изменилось. Приняв y пачек за одну часть, получим, что обычного порошка стало 2 y пачек, необычного 5 y пачек и превосходного 8 y пачек. Согласно условию задачи имеем систему: 3x 0,3x 2 y, 2,7x 2y, или 4x 55 5y 4x 55 5y. Решим полученную систему способом сложения. Умножим обе части первого уравнения на ( 2,5) и сложим полученное уравнение со вторым уравнением системы. Имеем: 2,75x 55, откуда x 20. Следовательно, y 27. Итак, мы определили, что первоначально на одну часть приходилось 20 пачек, а после изменения 27 пачек. Всего в магазине стало 15 y пачек порошка, т.е. 405 пачек. Ответ: 405 пачек. Задачи для самостоятельного решения 1. Гречневая крупа содержит 12% белков, 64% углеводов, остальное составляют другие продукты. Сколько белков и углеводов в гречневой крупе, если других продуктов в ней содержится 18кг? 16
17 2. Из двух городов, расстояние между которыми 420км, выехали одновременно навстречу друг другу легковая и грузовая машины. Скорость легковой машины 80км/ч, а скорость грузовой машины составляет 75% скорости легковой. Через сколько часов машины встретятся? 3. В первый день в магазине было продано 170кг картофеля, а во второй на 40% больше. Сколько килограммов картофеля продано за два дня? 4. Геракл и Ясон со своими аргонавтами плыли на корабле «Арго» в Колхиду за золотым руном. В первый день они проплыли 30% всего пути и ещё 10км, во второй часть пути и ещё 26км, а в третий 10% пути и оставшиеся 20км. Определить весь пройденный путь аргонавтами? Сколько километров преодолели аргонавты за третий день? 5. В двух бидонах всего было 51 литр молока. Если из первого бидона перелить 15% находящегося в нем молока во второй бидон, то в обоих бидонах молока будет поровну. Сколько литров молока было в каждом бидоне? 6. Для предохранения от замерзания оконные стекла смазывают раствором, содержащим по массе 9 частей глицерина, 5 частей поваренной соли и 6 частей воды. Найдите процентный состав раствора. 7. Пешеход прошел 15,5км за три часа. Во второй час он прошел в 1,2 раза больше, чем в первый час, а в третий час он прошел 90% того, что в первый час. Какое расстояние проходил пешеход в каждый час? 8. Имеются два сплава, в одном из которых содержится 30%, а во втором 50% золота. Сколько килограммов второго сплава нужно добавить к 10кг первого, чтобы получить сплав, содержащий 42% золота? 17
18 9. Свежие грибы содержат 90% воды, а сухие 12% воды. Сколько получится сухих грибов из 22кг свежих? 10. Если удлинить бороду Деду Морозу на 12см, а косу Снегурочке на 10%, то коса станет вдвое длиннее бороды. Если же Дед Мороз укоротит Снегурочке её косу на 10%, а она в ответ обрежет бороду Деда Мороза на 8см, то коса станет втрое длиннее бороды. Найти длину бороды Деда Мороза и длину косы Снегурочки. 11. Руда содержит 40% примесей, а выплавленный из неё металл содержит 4% примесей. Сколько получится металла из 24 тонн руды? 12. Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, а второй 26% меди. Процентное содержание цинка в первом и во втором сплавах одинаково. Сплавив 150кг первого сплава и 250кг второго, получили новый сплав, в котором оказалось 30% цинка. Определить, сколько килограммов олова содержится в получившемся новом сплаве. 13. К 8кг 70%-го раствора кислоты добавили 2кг воды. Определить процентную концентрацию полученного раствора. 14. На автостоянке стояли «Мерседесы», «Запорожцы» и прочие иномарки в количественном соотношении 2 : 3 : 6. После того как на стоянку подъехало некоторое количество «Мерседесов» и 33 «Запорожца», а 40% прочих иномарок уехало, количественное соотношение стало 5 : 7 : 4. Сколько «Мерседесов» стало на стоянке? 15. Алена, Валя и Наташа собирали клубнику. Валя собрала на 20% больше, чем Алена, но на 20% меньше, чем Наташа. На сколько процентов больше, чем Алена, собрала клубники Наташа? Специализированный учебно-научный центр НГУ,
🎦 Видео
Задача на проценты - три способа решенияСкачать

Математика 6 класс (Урок№51 - Решение задач с помощью уравнений. Часть 1.)Скачать

Алгебра 7 класс (Урок№44 - Решение задач с помощью линейных уравнений.)Скачать

Решение задач с помощью уравнений.Скачать

МЕРЗЛЯК-7. РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ ПАРАГРАФ-3 ЧАСТЬ-2Скачать

Решение задач на проценты способом пропорции. 6 класс.Скачать

Как решать задачи с процентами #математика #проценты #задачи #репетитор #репетиторматематикаСкачать

18. Решение задач на проценты с помощью уравнения.Скачать

Решение задач на процентыСкачать

Решение задач с помощью уравнений | Алгебра 7 класс #19 | ИнфоурокСкачать

РЕШЕНИЕ ЗАДАЧ НА ДВИЖЕНИЕ С ПОМОЩЬЮ УРАВНЕНИЙ. Примеры | АЛГЕБРА 7 классСкачать

Решение задач с помощью уравнений. Видеоурок 29. Математика 6 классСкачать

Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать




