На этой странице вы найдете готовые примеры по базовому разделу дискретной математики: элементам теории множеств. Типовые задачи снабжены подробным решением, формулами, пояснениями. Используйте их, чтобы научиться решать подобные задачи или закажите решение своей работы нам.
Основные темы (множества) : задание множеств, действия с множествами (пересечение, объединение, разность, дополнение); формула включений-исключений и применение для практических задач; декартово произведение множеств, мощность множества, построение диаграмм Эйлера-Венна.
Видео:Круги Эйлера. Логическая задача на множества. Иностранные языкиСкачать

Задачи с решениями о множествах онлайн
Задача 1. Начертите фигуры, изображающие множества 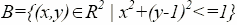
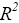
Задача 2. Докажите тождество
Задача 3. Установите взаимно однозначное соответствие между всеми прямыми на плоскости и всеми точками координатной оси Ох.
Задача 4. М — подмножество множества натуральных чисел. 10 элементов множества являются простыми числами, а остальные кратны либо 2, либо 3, либо 5. Определить мощность множества , если оно содержит: 70 чисел кратных 2; 60 чисел кратных 3; 80 числе кратных 5; 98 чисел кратных или 2 или 3; 95 чисел кратных или 2 или 5; 102 числа кратных или 3 или 5; 20 чисел, кратных 30.
Задача 5. Проверить справедливость тождеств или включений, используя алгебру множеств и диаграммы Эйлера-Венна.
Задача 6. Записать множества $A, B, C$ перечислением их элементов и найти . если
$A$ — множество корней уравнения $x^2-12x-28=0$,
$B$ — множество делителей числа 28,
$C$ — множество нечетных чисел $X$, таких что $0 le X le 7$.
Задача 7. Задано универсальное множество $U=$ и множества $X=$, $Y=$, $Z=$. Записать булеан множества $X$, любое разбиение множества $Y$, покрытие множества $Z$. Выполнить действия $(X setminus Y)cap bar Z$.
Задача 8. Решить задачу, используя диаграмму Эйлера-Венна.
Четырнадцать спортсменов участвовали в кроссе, 16 – в соревнованиях по плаванию, 10 – в велосипедных гонках. Восемь участников участвовали в кроссе и заплыве, 4 – в кроссе и велосипедных гонках, 9 – в плавании и велосипедных гонках. Во всех трех соревнованиях участвовали три человека. Сколько всего было спортсменов?
Задача 9. Пусть $Р(А)$ – множество всех подмножеств множества $А$. В каждом из следующих упорядоченных множеств укажите все минимальные и все максимальные элементы; найдите наибольший и наименьший элементы, если они есть, или докажите их отсутствие:
Задача 10. В химическом продукте могут оказаться примеси четырёх видов – $a,b,c,d$. Приняв в качестве исходного множества $М = $, образуйте множество всех его подмножеств $В(М)$. Дайте содержательную интерпретацию этого множества и его элементов. Каким ситуациям соответствуют, в частности, несобственные подмножества?
Видео:Операции над множествамиСкачать

Решение задач о множествах на заказ
Выполняем для студентов очников и заочников решение заданий, контрольных и практических работ по любым разделам теории множеств. Также оказываем помощь в сдаче тестов. Подробное оформление, таблицы, графики, пояснение, использование специальных программ при необходимости. Стоимость примера от 100 рублей , оформление производится в Word, срок от 2 дней.
Видео:Множества и операции над нимиСкачать

Решение некоторых задач по теории множеств
Разделы: Математика
На математическом кружке вместе с учащимися рассматривался ряд задач, благодаря наглядности которых, процесс решения становится понятным и интересным. На первый взгляд им хочется составить систему уравнений, но в процессе решения остается много неизвестных, что ставит их в тупик. Для того, чтобы уметь решать эти задачи, необходимо предварительно рассмотреть некоторые теоретические разделы теории множеств.
Введем определение множества, а так же некоторые обозначения.
Под множеством мы будем понимать такой набор, группу, коллекцию элементов, обладающих каким-либо общим для них всех свойством или признаком.
Множества обозначим А, В, С…, а элементы множеств а, b, с…, используя латинский алфавит.
Можно сделать такую запись определения множества:

“
” – принадлежит;
“=>“ – следовательно;
“ø” – пустое множество, т.е. не содержащее ни одного элемента.
Два множества будем называть равными, если они состоят из одних и тех же элементов
Если любой элемент из множества А принадлежит и множеству В, то говорят, что множество А включено в множество В, или множество А является подмножеством множества В, или А является частью В, т.е. если 

Графически это выглядит так (рис.1):
Можно дать другое определение равных множеств. Два множества называются равными, если они являются взаимными подмножествами.
Рассмотрим операции над множествами и их графическую иллюстрацию (рис.2).
Объединением множеств А и В называется множество С, образованное всеми элементами, которые принадлежат хотя бы одному из множеств А или В. Слова “или ” ключевое в понимании элементов входящих в объединение множеств.
Это определение можно записать с помощью обозначений:
А υ В, где
где “ υ ” – знак объединения,
“ / ” – заменяет слова ”таких что“
Пресечение двух множеств А и В называется множество С, образованное всеми элементами, которые принадлежат и множеству А, и множеству В. Здесь уже ключевое слово “и”. Запишем коротко:
А ∩ В = С, где
“∩“ – знак пересечения. (рис.3)
Обозначим буквой Е основное или универсальное множество, где 



Множество всех элементов универсального множества Е, не принадлежащих множеству А называется дополнением множества А до Е и обозначается Ā Е или Ā (рис.4)

Примерами для понимания этих понятий являются свойства:
А 
Свойства дополнения имеют свойства двойственности:
А
А
Введем еще одно понятие – это мощность множества.
Для конечного множества А через m (A) обозначим число элементов в множестве А.
Из определение следуют свойства:
Для любых конечных множеств справедливы так же утверждения:
m (A
m (A∩B) = m (A) + m (В) – m (А
m (A

А теперь рассмотрим ряд задач, которые удобно решать, используя графическую иллюстрацию.
Задача №1
В олимпиаде по математике для абитуриентов приняло участие 40 учащихся, им было предложено решить одну задачу по алгебре, одну по геометрии и одну по тригонометрии. По алгебре решили задачу 20 человек, по геометрии – 18 человек, по тригонометрии – 18 человек.
По алгебре и геометрии решили 7 человек, по алгебре и тригонометрии – 9 человек. Ни одной задачи не решили 3 человека.
- Сколько учащихся решили все задачи?
- Сколько учащихся решили только две задачи?
- Сколько учащихся решили только одну задачу?
Задача № 2
Первую или вторую контрольные работы по математике успешно написали 33 студента, первую или третью – 31 студент, вторую или третью – 32 студента. Не менее двух контрольных работ выполнили 20 студентов.
Сколько студентов успешно решили только одну контрольную работу?
Задача № 3
В классе 35 учеников. Каждый из них пользуется хотя бы одним из видов городского транспорта: метро, автобусом и троллейбусом. Всеми тремя видами транспорта пользуются 6 учеников, метро и автобусом – 15 учеников, метро и троллейбусом – 13 учеников, троллейбусом и автобусом – 9 учеников.
Сколько учеников пользуются только одним видом транспорта?
Решение задачи № 1
Запишем коротко условие и покажем решение:
- m (Е) = 40
- m (А) = 20
- m (В) = 18
- m (С) = 18
- m (А∩В) = 7
- m (А∩С) = 8
- m (В∩С) = 9
m (А



Обозначим разбиение универсального множества Е множествами А, В, С (рис.5).
К 1 – множество учеников, решивших только одну задачу по алгебре;
К 2 – множество учеников, решивших только две задачи по алгебре и геометрии;
К 3 – множество учеников, решивших только задачу по геометрии;
К 4 – множество учеников, решивших только две задачи по алгебре и тригонометрии;
К 5 – множество всех учеников, решивших все три задачи;
К 6 – множество всех учеников, решивших только две задачи, по геометрии и тригонометрии;
К 7 – множество всех учеников, решивших только задачу по тригонометрии;
К 8 – множество всех учеников, не решивших ни одной задачи.
Используя свойство мощности множеств и рисунок можно выполнить вычисления:
- m (К 5 ) = m (А∩В∩С)= m (А
В
С) — m (А) — m (В) — m (С) + m (А∩В) + m (А∩С) + m (В∩С)
- m (К 5 ) = 37-20-18-18+7+8+9=5
- m (К 2 ) = m (А∩В) — m (К 5 ) = 7-5=2
- m (К 4 ) = m (А∩С) — m (К 5 ) = 8-5=3
- m (К 6 ) = m (В∩С) — m (К 5 ) = 9-5=4
- m (К 1 ) = m (А) — m (К 2 ) — m (К 4 ) — m (К 5 ) = 20-2-3-5=10
- m (К 3 ) = m (В) — m (К 2 ) — m (К 6 ) — m (К 5 ) = 18-2-4-5=7
- m (К 7 ) = m (С) — m (К4) — m (К 6 ) — m (К 5 ) = 18-3-4-5 =6
- m (К 2 ) + m (К 4 ) + m (К6) = 2+3+4=9 – число учеников решивших только две задачи;
- m (К 1 ) + m (К 3 ) + m (К 7 ) = 10+7+6=23 – число учеников решивших только одну задачу.
Ответ:
5 учеников решили три задачи;
9 учеников решили только по две задачи;
23 ученика решили только по одной задаче.
С помощью этого метода можно записать решения второй и третьей задачи так:
Решение задачи № 2
- m (А
В) = 33
- m (А
С) = 31
- m (В
С) = 32
- m (К 2 ) + m (К 4 ) + m (К 6 ) + m (К 5 ) = 20
Найти m (К 1 ) + m (К 3 ) + m (К 7 )
- m (АUВ) = m (К 1 ) + m (К 2 ) + m (К 3 ) + m (К 4 ) + m (К 5 ) + m (К 6 ) = m (К 1 ) + m (К 3 ) + 20 = 33 =>
- m (К 1 ) + m (К 3 ) = 33 – 20 = 13
- m (АUС) = m (К 1 ) + m (К 4 ) + m (К 2 ) + m (К 5 ) + m (К 6 ) + m (К 7 ) = m (К 1 ) + m (К 7 ) + 20 = 31 =>
- m (К 1 ) + m (К 7 ) = 31 – 20 = 11
- m (ВUС) = m (К 3 ) + m (К 2 ) + m (К 5 ) + m (К 6 ) + m (К 7 ) + m (К 4 ) = m (К 3 ) + m (К 7 ) + 20 = 32 =>
- m (К 3 ) + m (К 7 ) = 32 – 20 = 12
- 2m (К 1 ) + m (К 3 ) + m (К 7 ) = 13+11=24
- 2m (К 1 ) + 12 = 24
- m (К 3 )= 13-6=7
- m (К 7 )=12-7=5
- m (К 1 ) + m (К 3 ) + m (К 7 ) = 6+7+5=18
Ответ:
Только одну контрольную работу решили 18 учеников.
Решение задачи № 3
- m (Е) = 35
- m (А∩В∩С)= m (К 5 ) = 6
- m (А∩В)= 15
- m (А∩С)= 13
- m (В∩С)= 9
Найти m (К1) + m (К3) + m (К 7 )
- m (К 2 ) = m (А∩В) — m (К 5 ) = 15-6=9
- m (К 4 ) = m (А∩С) — m (К 5 ) = 13-6=7
- m (К 6 ) = m (В∩С) — m (К 5 ) = 9-6=3
- m (К 1 ) + m (К 3 ) + m (К 7 ) = m (Е) — m (К 4 ) — m (К 2 ) — m (К 6 ) — m (К 5 ) = 35-7-9-3-6=10
Ответ:
Только одним видом транспорта пользуется 10 учеников.
Литература: А.Х. Шахмейстер «Множества. Функции. Последовательности»
Видео:Подмножество. Операции над множествами (пересечение, объединение множеств) – 8 класс алгебраСкачать

Задания 1. Теория множеств.
Вот мы все и добрались до первого листка с настоящими заданиями. Как их выполнять, что делать? В первой части вы найдёте список задач, которые предлагается выполнить. Очень рекомендуем хотя бы попытаться решить их самостоятельно, попробовать разные подходы, обсудить с друзьями или взять тетрадку с собой во время прогулки в парк. Самые нетерпеливые (а также те, кто достиг успехов в решении), могут прокрутить страницу ниже, где обнаружат максимально подробное решение каждой из задач. Надеемся, они вам помогут. Если что не ясно — спрашивайте в комментариях. Удачи!
Задача 1
Записать элементы множества 


Задача 2
Теперь давайте докажем три более абстрактных тезиса: 1) 


Задача 3
В гимназии учатся 




Задача 4
Ещё раз вспомните из лекции, что такое мощность множества. А теперь давайте попробуем доказать справедливость равенства 
Задача 5
Пол комнаты площадью в шесть квадратных метров полностью покрыт тремя коврами, площадь каждого из которых равна три квадратных метра. Докажите, что какие-то два из этих ковров перекрываются по площади, не меньшей одного квадратного метра.
Задача 6
Лесник считал сосны в лесу. Он обошёл территории, условно обозначенными кругами на рисунке ниже, и внутри каждого круга насчитал ровно пять сосен. Мог ли получиться у лесника на самом деле такой результат, или он ошибся?
Задача 7
Пусть от нас требуется показать истинность утверждения 
Задача 8
Если 

SPOILER ALERT! ДАЛЬШЕ ИДУТ РЕШЕНИЯ, НАСТОЯТЕЛЬНО РЕКОМЕНДУЕМ СНАЧАЛА ПОПРОБОВАТЬ!
Задача 1
Записать элементы множества 


Рассмотрим первый случай — мы имеем дело с объединением множеств, и в объединении, например, множеств 




В итоге получим
По второму пункту мы, фактически, ответ уже нашли —ведь в пересечение множеств входят общие элементы этих множеств, а мы их уже установили — это 

В третьем случае от нас требуется узнать разность множеств: 









В итоге получаем, что 
А что же от нас требуют в последнем случае? 



Введём понятие универсального множества 


Мы предположим, что универсальное множество в данном случае состоит из всех элементов, которые указаны в условии задачи — нетрудно видеть, что в таком случае универсальное множество 

Значит, осталось лишь найти разность 


Значит,
Задача 2
Теперь давайте докажем три более абстрактных тезиса: 1) 


Случай первый. Опираясь на выводы предыдущей задачи, мы понимаем, что 

На картинке прямоугольник представляет собой универсальное множество 


Теперь разность между прямоугольником и кругом должна стать «исходным» множеством. Где же будет его дополнение? Правильно, в круге!
Более формально это можно установить следующим образом. По определению, если 



Но в таком случае что мешает нам распространить ту же логику на дополнение дополнения? Если 



Совмещаем оба полученных результата: с одной стороны, если 



Случай второй. По определению универсального множества, абсолютно все элементы в нашем рассмотрении принадлежат множеству 

Случай третий. По аналогии: если к множеству не относится ни один из элементов, рассматриваемых нами, то это пустое множество. Но это значит, что абсолютно все элементы, о которых мы можем помыслить в рамках нашей задачи, относятся к дополнению этого множества (дополнению пустого множества). Значит, дополнение пустого множества совпадает с универсальным множеством.
Задача 3
В гимназии учатся 




Число всех учеников в данном случае можно представить как универсальное множество 
Итак, нам известно, что все из 200 учеников знают по крайней мере либо греческий язык, либо латынь. Однако если мы предположим, что эти множества не пересекаются, и сложим число знатоков греческого с числом знатоков латыни, мы получим 
Как же выяснить, сколько людей входят в это пересечение двух множеств? Мы знаешь лишь один критерий, по которому можно это установить — пойти от обратного, для начала выявив число знатоков только одного языка. Ведь те, кто знают только один язык, в пересечение точно не войдут!
Кто же не знает греческий? 






Выходит, что 

Задача 4
Ещё раз вспомните из лекции, что такое мощность множества! А теперь давайте попробуем доказать справедливость равенства

Ух, сложно! Но давайте начнём разбираться последовательно. Эта формула имеет вид для трёх произвольных множеств. Но вовсе не обязательно сразу рваться в бой — можно приступить к задаче с рассмотрения самого простого случая, а затем «насытить» наш анализ дополнительными моментами. Случай с одним множеством, правда, рассматривать бессмысленно — уж слишком он тривиален. Поэтому предлагаем подумать, как посчитать число элементов множеств, если их всего два.
Допустим, что эти множества не пересекаются. Тогда сумма числа их элементов находится легко — просто складываем в одну кучу все подряд элементы из обеих множеств.
Но что будет, если пересечение всё-таки имеет место быть? Из первой задачи мы видели, что в таком случае, если просто сложить все элементы из первого и второго множества, неизбежна ситуация повторного счёта. Для того, чтобы этого избежать, в задаче 1 нам пришлось обратить внимание на объединение множеств и сойтись на том, что элементы этого подмножества должны считаться лишь единожды, а не дважды.
В общем случае действует та же самая логика. Какие-то элементы у нас неизбежно засчитаются дважды — это будут те из них, которые содержатся одновременно и в 



Обобщим данное правило вычисления в формуле 
Ну а теперь можно перейти к трём множествам. Как вы, наверное, уже догадались, в этом случае можно предположить гораздо более разнообразные случаи пересечения множеств 


В частности, возможны сочетания 



Какие именно из этих пересечений пустые, а какие нет, мы знать заведомо не можем. Однако если какие-то из них не пустые, то мы должны их грамотно вычитать (или прибавлять), чтобы по-прежнему избегать возможности повторного (а то и тройного) счёта.
Как и в предыдущем случае, мы должны вычитать пересечения двух множеств — даже если этого пересечения нет, от вычитания нуля нам хуже не станет. По умолчанию будем исходить из того, что в результате сложения 


Изобразим этот случай — когда есть попарные пересечения, но нет пересечения тройного:
Однако у нас есть ещё один вариант пересечения — сразу всех трёх множеств вместе! В случае наличия трёх множеств 



Хорошо, скажете вы, но что же делать с этим пересечением этих трёх множеств? Прибавлять число элементов, входящих в это множество, или отнимать?
Для того, чтобы ответить на этот вопрос, необходимо хорошенько подумать, сколько раз у нас «считались» и вычитались элементы, входящие в это самое 





Обратите внимание, что количество слагаемых точно соответствует числу пересечений и разностей множеств на изображении выше.
PS. Этот случай можно распространить и на большее число множеств, но тогда нам нужно будет пересчитывать все комбинации из двух, трёх… и 
Подумайте: если у нас было бы не три, а четыре множества, то получилось бы, что при учёте четырёхкратного пересечения 


Отсюда общая формула:
Задача 5
Пол комнаты площадью в шесть квадратных метров полностью покрыт тремя коврами, площадь каждого из которых равна три квадратных метра. Докажите, что какие-то два из этих ковров перекрываются по площади, не меньшей одного квадратного метра.
Один из часто используемых методов в математических доказательствах — движение от обратного. Мы его уже однажды применили. Попробуем применить его и здесь. Допустим для начала, что площадь покрывается коврами вполне возможна без перекрытия вообще (без пересечения).
Мы знаем, что площадь каждого из трёх ковров составляет 


Тогда давайте предположим, что площадь каждого из попарных перекрытий ковров (первый с третьим, второй с третьим, второй с первым) может составлять меньше одного квадратного метра. И снова мы вводим предположение, обратное тому, которое мы хотим доказать.
Действительно, обратите внимание: чтобы опровергнуть тезис «какие-то два из этих ковров обязательно перекрываются по площади, не меньшей одного квадратного метра», нам нужно продемонстрировать, что абсолютно все перекрытия неизбежно имеют площадь, меньшую чем один квадратный метр. Обзовём последнее нашим условием-гипотезой.
Допустим, что какие-то два ковра перекрываются таким образом, чтобы удовлетворять данному условию. Есть ковёр 


В таком случае их общая площадь обязательно должна превышать 5 кв. м, но не быть более 6 кв. м (потому что оба ковра не крупнее трёх квадратных метров каждый). Таким образом, их общая площадь равна 
Теперь перейдём к третьему ковру. Опять же по нашему предположению от обратного, он должен иметь общую площадь с первым ковром меньшую, чем квадратный метр (обозначим её как 








Однако площадь, покрытая первыми двумя коврами, составляет 

Задача 6
Лесник считал сосны в лесу. Он обошёл территории, условно обозначенными кругами на рисунке ниже, и внутри каждого круга насчитал ровно пять сосен. Мог ли получиться у лесника на самом деле такой результат, или он ошибся?
Опять же можно пойти уже исследованным нам ходом рассуждения — движением от противного. Если в каждом круге действительно по пять сосен, то, если собрать вместе все маленькие круги, таких деревьев должно быть как минимум 15. Однако большие круги свидетельствуют о не более чем 10 соснах, что входит в противоречие с предыдущим утверждением.
Альтернативно можно обнаружить противоречие, наблюдая за расположением деревьев в пересечениях множеств. Малые левый и правый круги располагаются таким образом, что других сосен в больших кругах быть не должно. Но если это так, то на центральный малый круг не хватит вообще ни одной сосны, что опять же противоречит условию. Это хорошо видно на рисунке выше.
Задача 7
Пусть от нас требуется показать истинность утверждения:
Внимательно рассмотрим, для каких элементов у нас будет выполняться выражение в левой части тождества. Опять же, первым делом нам необходимо вспомнить определения. 









В данном случае розовым цветом обозначено множество, «остающееся» после разности.
Аналогично рассуждение для 


Выходит, из обеих вышеуказанных множеств исключается одно и то же пересечение 
Однако третья скобка в исходном выражении как раз и возвращает нам утерянное: 





Задача 8
Если 

Ранее мы видели, что в сложных утверждениях на языке теории множеств одновременно может предполагаться огромное количество различных ситуаций: какие-то множества пересекаются друг с другом, какие-то лежат внутри друг друга или, наоборот, располагаются порознь. Каждая из таких ситуаций образует частный случай записанного утверждения, и порой перебрать все из них тяжело. Как же доказывать такие утверждения, не тратя слишком много времени и сил? Рассуждая по существу с помощью формальной записи всех условий. Мы это проделывали уже раньше, но теперь сделаем это в более явном виде.
В данном случае нам нужно фактически показать, что при предпосылке 


Расшифруем первое выражение 


Теперь обратим внимание на то, выполняется ли при этой предпосылке 









Соответственно, с учётом условия 




Задача 9
Доказать справедливость выражения
Для начала вспомним, что означает разность множеств. В данном это значит, что некий элемент 


Теперь давайте хорошенько осознаем, что именно за выражение сформулировано в нашем задании. Нам необходимо установить, что в случае, если элемент входит в множество 

В этом заключается смысл выражения, истинность которого нам необходимо установить.
Итак, мы исходим из того, что какой-то элемент 

В нашей задаче фигурирует также множество 


Если 



Теперь рассмотрим другой случай: пусть 
Опять обратимся к нашей предпосылке, которая гласит, что 





Таким образом, мы исчерпали все возможные состояния, которые может принимать 


А почему из выполнения хотя бы одного из двух этих условий следует и выполнение 
Потому что мы в данном случае имеем объединение — а оно у нас «имеет силу» тогда, когда выполняется хотя бы что-то одно: либо истинно выражение слева от нашей подковы (в данном случае 

Опять же, в нашем случае невозможно, чтобы оба условия не выполнялись одновременно, ибо каждому из них соответствует один из двух случаев: либо 



📽️ Видео
9 класс, 2 урок, Множества и операции над нимиСкачать

Множества. Операции над множествами. 10 класс алгебраСкачать

Простейшие операции над множествамиСкачать

Задачи на множества. Мощность множеств. Математика 6 класс. Теория множествСкачать

Операции над множествамиСкачать

3.10 Пример - доказательство равенства двух множествСкачать
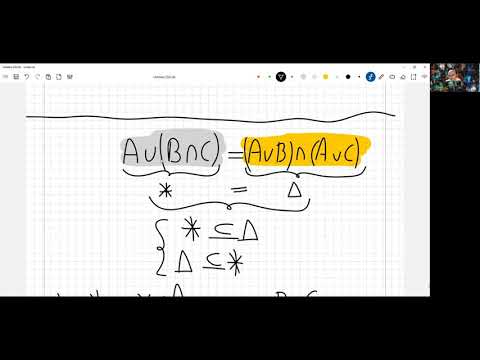
Пересечение и объединение множеств.Решение примеровСкачать

Пересечение множеств. Объединение множеств. 5 класс.Скачать

4. Множества. Операции над множествами. Дискретная математикаСкачать

Отношения множеств. Прямое произведение множествСкачать

Доказать равенства при помощи диаграмм Эйлера-Венна. Действия над множествами.Скачать

Преобразование логических выражений / Упрощение выражений (практика) [Алгебра логики] #6Скачать
![Преобразование логических выражений / Упрощение выражений (практика) [Алгебра логики] #6](https://i.ytimg.com/vi/S2bMFkhdA9Y/0.jpg)
Математика это не ИсламСкачать

Множества и операции над множествамиСкачать

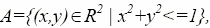
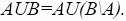
 ” – принадлежит;
” – принадлежит; 























