Решение задач физики дифференциальные уравнения

Примеры решения задач по механике, требующих интегрирования дифференциальных уравнений

(Задачи взяты из задачника: И.В. Мещерский «Сборник задач по теоретической механике», М.: Наука, 1981г., 460с.)

Задача №1. Пример задачи, приводящей к интегрированию дифференциальных уравнений методом разделения переменных.

При движении тела в неоднородной среде сила сопротивления изменяется по закону Н, где v – скорость тела в м/с, а s – пройденный путь в метрах. Определить пройденный путь как функцию времени, если начальная скорость v ₀=5 м/с.

Будем считать, что движение происходит вдоль оси 0Х, и что при t =0 тело находилось в начале координат, тогда проекция на ось 0Х силы, действующей на тело, может быть записана в виде

.

С учётом этого выражения, имеем следующее уравнение движения (считая массу тела m =1 кг)

, (1)

которое дополняется начальными условиями

, (2)

Решение уравнения второго порядка (1) можно свести к двум последовательным интегрированиям дифференциальных уравнений первого порядка. Чтобы получить первое уравнение, перепишем (1) в виде:

, (3)

и домножим на dt левую и правую части (3), учитывая при этом, что dx = v_xdt , получим:

, или (4)

Это уравнение с разделяющимися переменными (вида (1.5) из Раздела №1 Части I ). Очевидно, что оно, дополняется начальным условием, следующим из (2):

(5)

Разделив переменные в (4), в соответствие с формулой (1.7):

,

вычисляя данные интегралы, получим частный интеграл уравнения (4) (в форме (В.4) из Введения к Части I ):

(6)

Выразив отсюда v_x , будем иметь частное решение уравнения (4) (в форме (В.6) из Введения к Части I ):

(7)

Заменяя теперь в (7)

,

мы снова получаем уравнение с разделяющимися переменными (вида (1.1) из Раздела №1 Части I )

(8)

Разделяя в (8) переменные, с учётом начального условия (2), ищем частный интеграл этого уравнения (в виде (1.4) из Раздела №1 Части I ):

(9)

Вычисляя интегралы в (9), получим:

(10)

— частный интеграл уравнения (8) в форме (В.4) из Введения к Части I. Выражая отсюда x , получим частное решение уравнения (8):

, (11)

которое одновременно является и частным решением уравнения движения (1), удовлетворяющим начальным условиям (2), то есть, представляет собой закон движения тела (координата x , (или в данном случае путь), как функция времени). Таким образом, решение исходного уравнения движения второго порядка (1) в процессе решения задачи было сведено к интегрированию двух уравнений первого порядка с разделяющимися переменными (4) и (8).

Задача №2. Пример задачи, приводящей к интегрированию линейного обыкновенного дифференциального уравнения первого порядка.

Тело К, размерами которого можно пренебречь, установлено в верхней точке А шероховатой поверхности неподвижного полуцилиндра радиуса R . Какую начальную горизонтальную скорость , направленную по касательной к цилиндру, нужно сообщить телу К, чтобы оно начав движение, остановилось на поверхности цилиндра, если коэффициенты трения скольжения при движении и покое одинаковы и равны .

Расставляем силы, действующие на тело, и записываем второй закон Ньютона:

Спроектируем данное равенство на направление движения и перпендикулярное ему. Эти направления указаны на рисунке векторами и . Таким образом, для описания движения мы используем естественный способ. В результате получим:

(1)

Здесь учтено, что центростремительное ускорение

,

.

Сделаем в первом уравнении в (1) замену переменной — перейдем от дифференцирования по времени к дифференцированию по углу :

(т.к. )

С учетом этой замены перепишем (1):

(2)

Домножая второе уравнение на , и вычитая из первого, получим:

(3)

Это уравнение типа (2.1) (из Раздела №2 Части I ), в котором независимой переменной вместо t является ; неизвестной функцией вместо ;

; .

Уравнение (3) дополняется начальным условием:

(4)

С учетом указанных обозначений, используя формулу (2.9) (из Раздела №2 Части I ), решение уравнения (3) можно записать в виде:

(5)

Вычисляя с помощью интегрирования по частям интервалы в (5) , окончательно получим:

(6)

По условиям задачи тело должно остановиться на поверхности; т.е. при каком-то угле .

Подставляя вместо в (6) выразим оттуда :

(7)

Значение угла можно выразить через , поскольку ;

то из уравнений (2) получим:

(8)

Отсюда: ;

(9)

;

из (7) будем иметь:

(10)

Следовательно, чтобы тело остановилось на шероховатой поверхности цилиндра, нужно, чтобы его начальная скорость не превосходила значение, определенного в (10).

Задача №3. Пример задачи, приводящей к решению линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами.

Тело массы 5 кг подвешено к концу пружины жёсткости 20 Н/м и помещено в вязкую среду. Период его колебаний в этом случае равен 10 с. Найти постоянную демпфирования, логарифмический декремент колебаний и период свободных колебаний.

Выберем начало координат в положении статического равновесия тела и расставим силы, действующие на тело в процессе колебаний (считаем, что тело в данный момент времени движется вверх). Если АВ обозначает длину нерастянутой пружины, то отрезок ОВ представляет статическое удлинение пружины под действием силы mg . По закону Гука mg = k × ОВ, где k — коэффициент жёсткости пружины. Записываем второй закон Ньютона:

.

Проектируем это равенство на ось ОХ, учитывая, что

, .

В результате получим уравнение колебаний

, или (1)

где , .

Уравнение (1) представляет собой однородное обыкновенное дифференциальное уравнение второго порядка с постоянными коэффициентами (уравнение (1.1) Части II ). Для его решения используем схему, описанную в Разделе №1 Части II .

Составляем характеристическое уравнение:

. (2)

Вычисляем дискриминант уравнения (2):

. (3)

Поскольку в данном случае, в соответствие с условиями задачи движение тела носит колебательный (периодический) характер, то его координата должна изменяться со временем по гармоническому закону, то есть по закону косинуса или синуса. Для того же, чтобы решение уравнения (1) выражалось через данные функции, мы должны считать, что D (4)

где величины и определяются следующим образом:

, (5)

В случае отсутствия затухания (когда n =0), , и тело совершает свободные колебания с периодом с.

Если же n ¹ 0, то период колебаний, с учётом (5),:

.

Выражаем отсюда , и определяем постоянную демпфирования a (коэффициент пропорциональности в формуле для силы сопротивления):

Подставляя данные задачи, получим a =19 .

В соответствие со своим определением, логарифмический декремент затухания есть натуральный логарифм отношения двух последовательных амплитуд, (то есть взятых через половину периода колебания ): . Вычисляя n и подставляя значение Т, получим =9,5.

Задача №4. Пример задачи, приводящей к решению линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.

Для уменьшения действия на тело массы m возмущающей силы устанавливают пружинный амортизатор с жидкостным демпфером. Коэффициент жёсткости пружины k . Считая, что сила сопротивления пропорциональна первой степени скорости ( ), найти максимальное динамическое давление всей системы на фундамент при установившихся колебаниях.

Направим ось 0 X вдоль направления движения, выбрав начало координат в положении статического равновесия тела. При этом считаем, что сила тяжести скомпенсирована силой статического сжатия пружины амортизатора. Записываем второй закон Ньютона:

.

Проектируем это равенство на ось ОХ, учитывая, что

, , .

В результате получим уравнение колебаний

, или , (1)

где обозначено , .

При колебаниях на фундамент действует сила, складывающаяся из силы деформации пружины и силы сопротивления, равная в соответствие с третьим законом Ньютона,

. (2)

Следовательно, для вычисления этой силы нужно знать уравнение движения тела , для чего необходимо решить уравнение (1). Поскольку в задаче рассматриваются уже установившиеся колебания, то есть рассматривается движение тела, установившееся по истечению достаточно большого промежутка времени от момента его начала. При этом тело будет совершать колебания с частотой вынуждающей силы. Поэтому мы должны найти частное решение уравнения (1), соответствующее этим вынужденным колебаниям. Для этого используем метод подбора по правой части. Представим, в соответствие с формулой (2.5) (из Раздела №2 Части II ) решение уравнения (1) в виде

(3)

Обозначим для краткости записи через и подставим (3) в (1):

Приравнивая коэффициенты при и , получим следующую систему уравнений:

Решая данную систему, находим

, (4)

Подставим (4) в (3):

(5)

Данную формулу, обозначая

, (6)

можно переписать в виде:

(7)

Подставим теперь (7) в (2):

(8)

, (9)

формулу (8) можно переписать в виде

(10)

Отсюда следует, что максимальное динамическое давление всей системы на фундамент равно

. (11)

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Решение задач физики дифференциальные уравнения

А. А. Гусак. Высшая математика. Том 2.
Глава 27. Простейшие дифференциальные уравнения математической физики

В этой главе рассматриваются некоторые уравнения математической физики, т.е. уравнения с частными производными второго порядка, к которым приводят следующие задачи: задача о колебаниях струны, задача о распространении тепла и др.

27.1. Вывод уравнения колебаний струны

Рассмотрим туго натянутую струну, закрепленную на концах. Выведем струну из положения равновесия (оттянув ее или ударив по ней), струна начнет колебаться.

Предположим, что любая точка струны колеблется по прямой, перпендикулярной к исходному положению струны, и струна все время находится в одной и той же плоскости.

Выберем в этой плоскости декартову прямоугольную систему координат Охu. В качестве оси Ох возьмем прямую, на которой находилась струна в положении равновесия, за ось Оu примем прямую, проходящую через левый конец струны и перпендикулярно к оси Ох (рис. 27.1).

Отклонение струны от положения равновесия обозначим через u; очевидно, u зависит от абсциссы х точки струны и времени t, т.е. u = u(х, t).

При фиксированном t графиком функции u = u(х, t) в плоскости Охu является форма струны в данный момент времени t. Угловой коэффициент касательной к графику в точке с абсциссой х равен частной производной по х от функции u(х, t) т.е.

где α = α (x, t) – угол наклона касательной.

Чтобы составить представление о колебаниях струны, необходимо начертить ряд графиков функции u = u(х, t) при различных значениях t.

При фиксированном значении х функция u = u(х, t) определяет закон движения точки с абсциссой х. Эта точка движется по прямой, параллельной оси Оu. Скорость и ускорение указанного движения выражаются соответственно формулами

Будем изучать малые колебания струны, т.е. такие, при которых угол α = α (x, t) (угол наклона касательной к графику функции u = u(х, t) при каждом фиксированном значении t) настолько мал, что его квадратом можно пренебречь, т.е. приближенно считать

то отсюда следует, что

sin α = α, cos α = 1.

tg α – sin α = tg α(1 – cos α) = tg α · 0 = 0 ,

Принимая во внимание (27.3) – (27.5), заключаем, что

tg² α = 0 , или

Следовательно, длина дуги струны, ограниченной точками M1(x1, u1), M2(x2, u2) выразится формулой

Соотношение (27.7) означает, что длина любого участка струны остается постоянной.

Будем предполагать струну абсолютно гибкой, что означает следующее: если удалить участки ОМ1, M2L (см. рис. 27.1), то их действия на участок М1М2 заменяются соответственно действием сил натяжения T1 и Т2, направленных по касательным к графику функции u = u(х, t) в точках М1 и М2 (рис. 27.2). Поскольку по предположению точки струны движутся по прямым, параллельным оси Оu, то сумма проекций сил T1, Т2 на ось Ох равна нулю. Проектируя эти силы на ось Ох, получаем T2сos α2 – T1cos α1 = 0, где T1, Т2 – величины сил T1, Т2.

На основании второго из равенств (27.4) заключаем, что T1 = T2 т.е. величина силы натяжения остается постоянной. Обозначая ее через T, получаем

Проектируя силы T1, Т2 на ось Оu, находим

С учетом равенства (27.1) получаем

где х – абсцисса точки М1; х + Δх – абсцисса точки М2.

Применяя теорему Лагранжа о конечном приращении дифференцируемой функции, находим, что

поэтому проекция сил натяжения T1 и Т2 на ось Ох выразится формулой

Предположим, что на струну действуют также внешние силы, параллельные оси Оu, плотность распределения* которых равна g(x, t), тогда величина равнодействующей этих сил, приложенных к участку М1М2, приближенно равна g(x, t)Δx. Силами сопротивления внешней среды пренебрегаем.

* Под плотностью понимают предел средней плотности распределения сил на данном отрезке, когда длина отрезка стремится к нулю; средняя плотность – отношение величины равнодействующей сил к длине отрезка, на котором они приложены.

Будем считать струну однородной, обозначим через ρ ее линейную плотность, тогда масса участка М1М2 выразится так: ρ М1М2 = ρ Δх, m = ρ Δх

В соответствии со вторым законом Ньютона mw = F (произведение массы на ускорение равно действующей силе) получаем

Уравнение (27.10) называется уравнением колебаний струны, или одномерным волновым уравнением.

Если g(x, t) = 0 (внешние силы отсутствуют), то уравнение (27.10) принимает вид

Уравнение (27.12) называется уравнением свободных колебаний, уравнение (27.10) — уравнением вынужденных колебаний струны.

27.2. Начальные и краевые условия. Задача Коши

Чтобы из множества решений уравнения с частными производными второго порядка выбрать определенное решение, необходимо задать дополнительные условия.

Так, в случае уравнения (27.10) или (27.12) нужно указать отклонение и скорость движения в начальный момент времени t0 (будем полагать t0 = 0), т.е.

где f(x), F(x) – заданные функции, а также зафиксировать отклонения концов струны. Поскольку концы закреплены, то

где l – длина струны.

Условия (27.13) называются начальными условиями, а условия (27.14) – краевыми (или граничными) условиями.

Итак, задача о свободных колебаниях струны ставится следующим образом. Найти решение u = u(х, t) линейного однородного уравнения с частными производными второго порядка , удовлетворяющее начальным условиям u(х, 0) = f(x), u'(х,0) = F(x) и краевым условиям u(0, t) = 0, u(l, t) = 0.

Функции f(х) и F(x) определены на отрезке [0, l], из краевых условий следует, что f(0) = 0, f(l) = 0. Можно доказать, что при некоторых предположениях относительно функций f(x) и F(x) поставленная задача имеет единственное решение.

В случае, когда предполагается, что струна является неограниченной, граничные условия не налагаются.

Задача о свободных колебаниях неограниченной струны ставится так. Найти решение u = u(х, t) уравнения с частными производными второго порядка , удовлетворяющее начальным условиям

где f(x) и F(x) – заданные функции, определенные на всей действительной оси. Эта задача называется задачей Коши.

27.3. Задача о свободных колебаниях бесконечной струны. Метод Д’Аламбера

Как уже отмечалось, задача о свободных колебаниях бесконечной струны, или задача Коши, состоит в следующем.

Найти решение u = u(х, t) линейного однородного уравнения

удовлетворяющее начальным условиям

где f(х), F(x) – заданные функции, определенные в бесконечном промежутке (-∞, +∞).

Уравнение (27.15) перепишем так: и (положив t = у) сравним его с уравнением (26.9). Поскольку В² — АС = а² > 0, то уравнение является уравнением гиперболического типа.

Уравнение характеристик Ady² — 2Bdxdy + Cdx² = 0 принимает вид a²dt² — dx² = 0 или dx² — a²dta² = 0. Оно распадается на два уравнения dx – adt = 0, dx + adt = 0, откуда получаем х – at = С1, х + at – С1.

Введя новые переменные ξ и η по формулам

преобразуем уравнение (27.15) к каноническому виду.

Выражаем частные производные по переменным х, t через частные производные по ξ, η :

Подставляя в уравнение (27.15) выражения для частных производных второго порядка, получаем

Проинтегрируем последнее уравнение. Положим тогда

Следовательно, , или u = φ(ξ) + ψ(η) , где φ(ξ), ψ(η) – произвольные дважды дифференцируемые функции своих аргументов. Принимая во внимание (27.17), последнюю формулу можно записать так:

Формула (27.18) определяет общее решение уравнения (27.15).

Среди всех этих решений найдем то, которое удовлетворяет условиям (27.16), Для функции (27.18) и ее частной производной по t

условия (27.16) принимают вид

Второе равенство проинтегрируем по отрезку [0, х]. Обозначив переменную интегрирования через z получим

где С = φ (0) + ψ (0)

Это уравнение и первое из уравнений (27.19) позволяют определить функции φ (x) и ψ (x):

Подставляя в эти формулы вместо х соответственно х – at и х + at, получаем

В соответствии сформулой (27.18) находим

Формула (27.20) представляет решение Д’Аламбера рассматриваемой задачи Коши для уравнения колебаний неограниченной струны. Читателю предлагается непосредственной проверкой убедиться в том, что функция (27.20) удовлетворяет уравнению (27.15) и условиям (27.16).

А. А. Гусак. Высшая математика. Том 2. Стр. 247-253.

Видео:Решение физических задач при помощи диффуров | Дифференциальные уравненияСкачать

Примеры решений задач по дифференциальным уравнениям

Теперь, когда вы научились находить производные и интегралы, самое время перейти к более сложной теме: решению дифференциальных уравнений (они же дифуры, диффуры и диф.уры :)), то есть уравнений, которые вместе с самой функцией (и/или аргументом), содержат и производную или даже несколько.

Как же решать дифференциальные уравнения? Главное, что понадобится, это а) умение правильно определить тип дифференциального уравнения и б) умение хорошо интегрировать — это существенная часть работы. А дальше следовать алгоримам для каждого из типов уравнений, которые подробно описаны в учебниках и ниже в примерах.

В этом разделе вы найдете решенные задачи на составление и решение дифференциальных уравнений. Примеры решений дифуров выложены бесплатно для вашего удобства и отсортированы по темам — изучайте, ищите похожие, решайте свои. Есть трудности в выполнении заданий? Мы готовы оказать помощь по дифференциальным уравнениям

Видео:Решение физических задач с помощью дифференциальных уравненийСкачать

Как решить дифференциальное уравнение онлайн?

Да ладно, неужели только вручную? Мучиться, определять тип, переносить, интегрировать, заменять, снова интегрировать, подставлять, выводить? Наверняка ведь есть онлайн-калькуляторы, которые позволяют решать дифференциальные уравнения?

У меня две новости, хорошая и плохая. Хорошая в том, что действительно самые распространенные типы дифференциальных уравнений математические программы умеют решать. Плохая в том, что обычно они выводят ответ (для научных расчетов этого достаточно), а не полное решение.

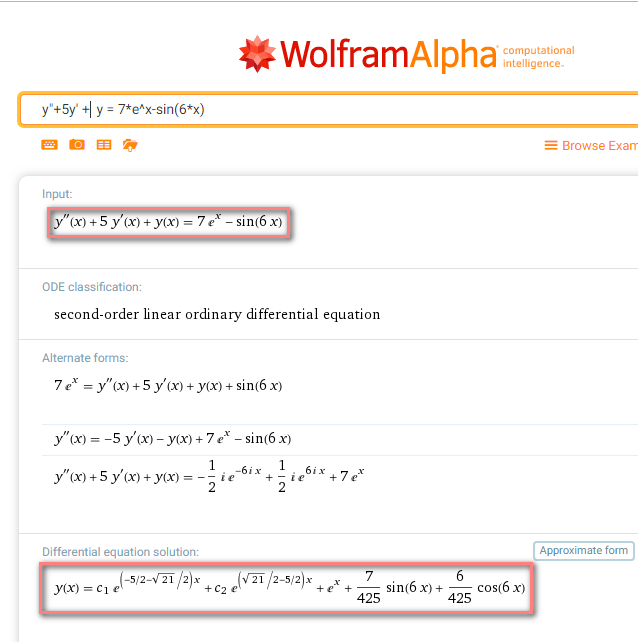
Есть известный математический сервис www.wolframalpha.com, которые представляет полные решения множества математических задач, в том числе диффуров онлайн (на английском языке) за 7 долларов в месяц. Ответы же доступны всем и могут помочь проверять правильность своего решения (см. ниже на скриншоте обведено само уравнение и его решение). Подробнее об этом сайте и типичных задачах, решаемых на нем, вы можете узнать тут.

Если вы забьете в поисковик что-то вроде «решить дифференциальное уравнение онлайн», то получите десятки ссылок на сайты, обещающие именно это.

Я проверила все сайты с первых страниц Яндекса и Гугла. Большая часть сайтов использует результаты расчетов www.wolframalpha.com (см. выше) и показывает вам ответ (и рекламу :)). Некоторые при этом не показывают даже ответа или говорят, что уравнение введено некорректно (хотя это вполне стандартное решаемое вручную линейное уравнение с постоянными коэффициентами). Полное решение не выдал ни один сайт.

Выводы? Бесплатно и полно и онлайн — не бывает. Хотите получать полные решения — используйте платную подписку на ВольфрамАльфа (или проконсультируйтесь у нас). Хотите ответы — там же бесплатно. Хотите научиться решать? Придется засучить рукава. Примеры на этой странице и ссылки внизу помогут вам. Удачи!

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Общий интеграл, семейство кривых

Задача 1. Показать, что функция $y^2-x^2-Cy=0$ является общим интегралом дифференциального уравнения $y'(x^2+y^2)-2xy=0.$

Задача 2. Составить дифференциальное уравнение семейства кривых $C_1 x+(y-C_2)^2=0.$

Видео:Задача на составление дифференциального уравненияСкачать

Решения дифференциальных уравнений 1 порядка

Задача 3. Найти общее решение линейного дифференциального уравнения первого порядка $ xy’+x^2+xy-y=0.$

Задача 4. Решить однородное дифференциальное уравнение $y’=-y/x quad (x ne 0).$

Задача 5. Решить дифференциальное уравнение $(y^4-2x^3y)dx+(x^4-2xy^3)dy=0.$

Задача 6. Решить однородное дифференциальное уравнение $(2x+y+1)dx+(x+2y-1)dy=0.$

Задача 7. Решить линейное дифференциальное уравнение первого порядка $y’-2xy=3x^2-2x^4.$

Задача 8. Решить дифференциальное уравнение $(x+y^2)y’=y-1.$

Видео:Дифференциальные уравнения | задача Штурма - Лиувилля | классические краевые задачи | 1Скачать

Решение задачи Коши для ДУ

Задача 9. Решить дифференциальное уравнение с разделяющимися переменными $(1+x^2)dy-2xydx=0.$ Найти частное решение, удовлетворяющее начальному условию $y(0)=1$.

Задача 10. Решить задачу Коши для дифференциального уравнения второго порядка $2y y» +1 =(y’)^2, , y(1/3)=1, , y'(1/3)=2$.

Задача 11. Найти решение задачи Коши для дифференциального уравнения $$ y’= frac, y(1)=1. $$

Задача 12. Решить задачу Коши для дифференциального уравнения третьего порядка $$ y»’=x+cos x, quad y(0)=0, y'(0)=0, y»(0)=0. $$

Видео:Решение физических задач с помощью дифференциальных уравнений. Часть 2Скачать

Решения дифференциальных уравнений 2 порядка

Задача 13. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами $y»+4y’+4y=xe^.$

Задача 14. Решить задачу Коши для дифференциального уравнения второго порядка с постоянными коэффициентами методом вариации: $$ y»-3y’=frac<9e^><3+e^>, quad y(0)=4ln 4, y'(0)=3(3ln 4-1). $$

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Cоставление дифференциальных уравнений

Задача 15. Скорость остывания нагретого тела пропорциональна разности температур тела и окружающей среды. За 10 минут тело охладилось от 100 до 60 градусов. Температура среды постоянна и равна 20 градусам. Когда тело остынет до 25 градусов?

Задача 16. Моторная лодка движется в спокойной воде со скоростью 5 м/сек. На полном ходу ее мотор выключается и через 40 сек после этого скорость лодки уменьшается до 2 м/сек. Определить скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости движения лодки.

Видео:Задача на составление Дифференциального уравненияСкачать

Решения нелинейных дифференциальных уравнений

Задача 17. Решить дифференциальное уравнение $y^2 ^2 -2xyy’+2y^2-x^2=0.$

Задача 18. Решить дифференциальное уравнение $^2-4xyy’+8y^2=0.$

📽️ Видео

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ решениеСкачать

Дифференциальные уравнения 1. Вязкое торможениеСкачать

Дифференциальные уравнения. 11 класс.Скачать

Решение задачи Коши дифференциального уравнения #maths #calculus #differentialequation #algebraСкачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Задача Коши для дифференциальных уравненийСкачать

2.1. Метод характеристик. Задача Коши для гиперболического уравнения на плоскости.Скачать

Д1 Дифференциальные уравнения движения материальной точкиСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать