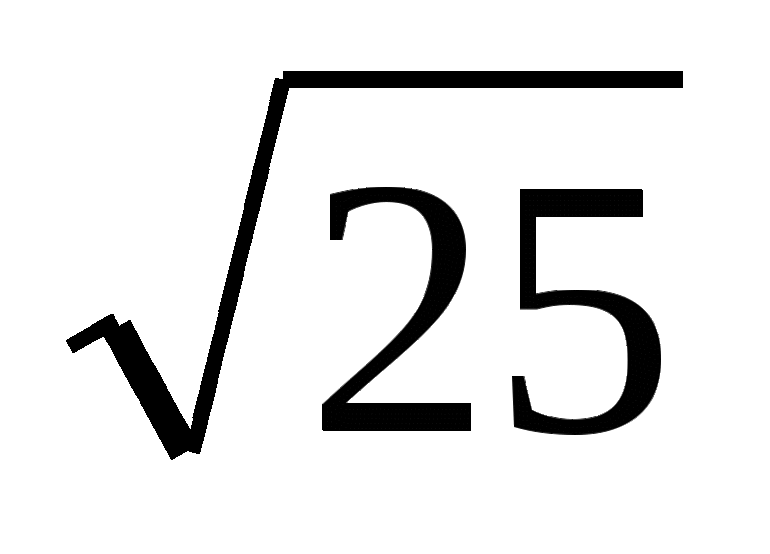Решение всех типов уравнений с параметром

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

«Основные типы задач с параметром и их решение»

Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Оглавление

Задачи с параметром — одна из самых интересных и многогранных тем в математике. Задачи с параметрами играют важную роль в формировании логического мышления и математической культуры у школьников, но их решение вызывает у них значительные затруднения. Это связано с тем, что каждое уравнение с параметрами представляет собой целый класс обычных уравнений, для каждого из которых должно быть получено решение.

Актуальность данной темы очевидна. Ведь уравнения и неравенства с параметром стали привычной частью всех сложных экзаменационных заданий и вступительных экзаменов в ВУЗы, а также задания данного типа являются неотъемлемой частью практически всех олимпиад разного уровня.

Проблема в том, что в школьной программе такие задачи встречаются редко, и только самые простые вариации. Многие учащиеся не до конца понимают, как решать задания такого типа. Учащиеся выпускных классов лишают себя возможности получить высокие баллы за задания этого типа.

Цель данной работы: изучение основных способов решения уравнений и неравенств с параметром, рассмотрение основных типов заданий в которых применяется параметр в школьной программе.

1) сбор и обработка материала по данной теме;

2) систематизация различных методов решения;

3) проведение мастер-класса по решению уравнений с параметром;

Объект исследования : уравнения и неравенства с параметром.

Предмет исследования : методы решений уравнений и неравенств, содержащих параметр.

Видео:Самая сложная тема из ЕГЭ. Задание с ПАРАМЕТРОМ | Математика TutorOnlineСкачать

Глава 1. Основные понятия.

Видео:Уравнения с параметром. Алгебра, 8 классСкачать

1.1 Что такое параметр.

Толковый словарь определяет параметр, как величину, характеризующую какое-нибудь основное свойство машины, устройства, системы или явления, процесса. Рассмотрение параметров — это всегда выбор. Покупая какую-либо вещь, мы внимательно изучаем ее основные характеристики. Так, приобретая компьютер, мы обращаем внимание на следующие его параметры: производительность, габариты, состав комплектующих, цену и др. Перед выбором мы стоим и в различных жизненных ситуациях.

Что такое параметр в математике? Если вы вспомните некоторые основные уравнения (например, kx+l=0, ax²+bx+c=0), то обратите внимание, что при поиске их корней значения остальных переменных, входящих в уравнения, считаются фиксированными и заданными. Все разночтения в существующей литературе связаны с толкованием того, какими фиксированными и заданными могут быть эти значения остальных переменных.

Поскольку в школьных учебниках нет определения параметра, возьмем за основу следующий его простейший вариант.

Определение: параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.

Независимость параметра заключается в его «неподчинении» свойствам, вытекающим из условия задачи. Например, из неотрицательности левой части уравнения |x|= a – 1 не следует неотрицательность значений выражения a – 1, и если a – 1

Видео:9 класс, 7 урок, Задачи с параметрамиСкачать

1.2 Что означает «решить задачу с параметром».

Естественно, это зависит от вопроса в задаче. Если, например, требуется решить уравнение, неравенство, их систему или совокупность, то это означает предъявить обоснованный ответ либо для любого значения параметра, либо для значения параметра, принадлежащего заранее оговоренному множеству.

Если же требуется найти значения параметра, при которых множество решений уравнения, неравенства и т. д. удовлетворяет объявленному условию, то, очевидно, решение задачи и состоит в поиске указанных значений параметра.

Отмечу сразу, что запись ответа – важнейший этап решения, отличающий задачу с параметром от других задач. Ответ в задаче с параметром – это описание множества ответов к задачам, полученным при конкретных значениях параметра.

Видео:✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive​​ #041 | Борис ТрушинСкачать

1.3. Основные типы задач с параметрами.

Тип 1. Уравнения и т.п., которые необходимо решить либо для любого значения параметра (параметров), либо для значений параметра, принадлежащих заранее оговоренному множеству.

Тип 2. Уравнения и т.п., для которых требуется определить количество решений в зависимости от значения параметра (параметров).

Тип 3. Уравнения и т.п., для которых требуется найти все те значения параметра, при которых указанные уравнения, неравенства, их системы и совокупности имеют заданное число решений (в частности, не имеют или имеют бесконечное множество решений).

Легко увидеть, что задачи типа 3 в каком-то смысле обратны задачам типа 2.

Тип 4. Уравнения и т.п., для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.

Например, найти значения параметра, при которых:

Многообразие задач с параметром охватывает весь курс школьной математики (и алгебры, и геометрии), но подавляющая часть из них на выпускных и вступительных экзаменах относится к одному из четырех перечисленных типов, которые по этой причине названы основными.

Видео:Задача 17 ЕГЭ профильный. Параметры с нуляСкачать

1.4 Основные способы решения задач с параметром.

Способ I (аналитический). Это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра. Иногда говорят, что это способ силового, в хорошем смысле «наглого» решения.

Аналитический способ решения задач с параметром есть самый трудный способ, требующий высокой грамотности и наибольших усилий по овладению им.

Способ II (графический). В зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a).

Способ III (решение относительно параметра). При решении этим способом переменные x и a принимаются равноправными, и выбирается та переменная, относительно которой аналитическое решение признается более простым. После естественных упрощений возвращаемся к исходному смыслу переменных x и a и заканчиваем решение.

Перейдем теперь к демонстрации указанных способов решения задач с параметром.

Видео:8 класс, 39 урок, Задачи с параметрамиСкачать

Глава 2. Основные способы решения задач с параметром

Видео:Уравнения с параметром. Алгебра 7 класс.Скачать

2.1 Аналитический способ.

Универсальных методов решения уравнений и неравенств с параметрами не существует. Одно из немногих исключений – линейные уравнения и неравенства.

Пример 1. Решить уравнение: а ( а – 2) х = а – 2.

Решение. Перед нами линейное уравнение, имеющее смысл при всех допустимых значениях а . Будем его решать «как обычно»: делим оби части уравнения на коэффициент при неизвестном.

Полное решение см. в приложении 1

Пример 2 . Решить неравенство ( а + 3) х а – 1.

Решение. Рассмотрим случаи:

1) а + 3 = 0, а = -3, тогда неравенство примет вид 0 ∙ х

2) а + 3 > 0, а > -3, тогда

Ответ: 1) если а = -3, то х – любое число;

Другое важное исключение – уравнения и неравенства, связанные с квадратичной функцией.

Пример3. Решить уравнение ( а – 2) х 2 + (2 а – 3) х + а + 2 = 0.

Решение рассмотрим в приложении 2.

Видео:Уравнения с параметром, изящное решениеСкачать

2.2 Графический способ.

Алгоритм графического решения уравнений с параметром:

-Находим область определения уравнения.

-Выражаем α как функцию от х.

-В системе координат строим график функции α (х) для тех значений х, которые входят в область определения данного уравнения.

-Находим точки пересечения прямой a = с, с графиком функции a (х). Если прямая a = с пересекает график a (х), то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение c = a (х) относительно х.

Рассмотрим на примерах:

Пример 1: Решить уравнение | x 2 – 2 x – 3| = a в зависимости от параметра а .

Решение. Понятно, что при а ≥ 0:

Но все ли корни подходят? Чтобы выяснить это, построим график функции а = | x 2 – 2 x – 3|. Количество корней можно увидеть на рисунке 1, мысленно проводя прямые линии, соответствующие значениям а . Получим:

если а = 0 и а > 4, то два корня.

Найдем эти корни:

При а = 0 получим x 2 – 2 x – 3 = 0,

уравнения x 2 – 2 x – 3 – а = 0.

4) при а = 4 – три корня:

x 2 – 2 x – 3 = 4 x 2 – 2 x – 3 = – 4 Ответ: 1) если a

x 2 – 2 x – 7 = 0 x 2 – 2 x + 1 = 0 2) если а = 0, то х ₁ = –1, х ₂ = 3;

Видео:Профильный ЕГЭ 2023 математика. Задача 17. Параметр. Аналитический методСкачать

2.3 Решение относительно параметра.

Если степень неизвестного слишком высока, а степень параметра не превосходит двух, то здесь эффективен метод решения уравнения (неравенства) относительно параметра.

Пример 1. Решить уравнение 2 х 3 – ( а + 2) х 2 – ах + а 2 = 0.

Решение. Перепишем уравнение в виде

Решим уравнение относительно параметра а.

D = ( х 2 + х ) 2 – 4(2 х 3 – 2 х 2 ) = х 2 ( х + 1) 2 – 8 х 2 ( х – 1) = х 2 ( х 2 + 2 х + 1 – 8 х + 8) = х 2 ( х 2 – 6 х + 9) = х 2 ( х – 3) 2

Осталось решить полученные уравнения относительно х .

Дальнейшее решение смотри в приложении 3.

Видео:Параметр, ЕГЭ №18 для Чайников, Урок 7Скачать

Заключение.

В процессе проделанной работы в соответствии с ее целями и задачами были получены следующие выводы и результаты:

1. Рассмотрели основные способы решения уравнений и неравенств с параметром:

— решение относительно параметра;

2. Графический метод является удобным и быстрым способом решения уравнений и систем уравнений с параметрами, но нельзя полностью представить себе сложность и нестандартность решения каждой задачи с параметром, изучая только графический способ. Нельзя научиться решать любые задачи с параметрами, используя какой-то алгоритм или формулы.

3. В заданиях ОГЭ по математике в 9 классе уравнения, системы уравнений с параметром проще, удобнее и нагляднее решать графическим способом. В связи с этим разработали ряд задач с параметром в помощь учителю и ученику (см. приложение 4). Разработанный ряд задач можно использовать на факультативах по математике при подготовке к ОГЭ, при подготовке к олимпиадам или для привития интереса к математике, совершенствования математической культуры, навыков дедуктивного мышления и творческих исследовательских способностей. Данный справочник предложен 9-классникам.

Планирую продолжить работу над этой темой, и расширить круг изучаемых типов заданий с параметрами.

Видео:Все уравнения с параметром на РешуЕГЭ. Тотальный разбор 17 номера ЕГЭ по математикеСкачать

Литература.

1. Алгебра. 9 класс. Учебник для учащихся общеобразовательных учреждений/ А.Г.Мордкович.- М.:Мнемозина, 2013;

2. Горнштейн П.И. «Задачи с параметрами. » Москва 2003г.;

3. Математика. 9 класс. Подготовка к ГИА – 2014: учебно-методические пособие/ Под ред.Ф.Ф.Лысенко, С.Ю.Кулабухова. – Ростов-на-Дону: Легион, 2013г.;

4. Математика. Подготовка к ЕГЭ-2013 : учебно-методические пособие/ Под ред.Ф.Ф.Лысенко, С.Ю.Кулабухова. – Ростов-на-Дону: Легион, 2012г.;

5. Солуковцева Л. «Линейные и дробно-линейные уравнения и неравенства с параметрами. Москва.2007г.;

6. Шарыгин И.Ф. Факультативный курс по математике: Решение задач: Учеб. Пособие для 10 кл. сред.шк. – М.: Просвещение, 1989.;

7. ЯстребинецкийГ.А.«Уравнения и неравенства, содержащие параметры», 1972г.

Видео:Математика | Параметр. Система уравнений с параметромСкачать

Задачи с параметрами на ЕГЭ по математике

Задача с параметрами – одна из самых сложных в ЕГЭ по математике Профильного уровня. Это задание №18

И знать здесь действительно нужно много.

Научиться строить графики всех элементарных функций (и отличать по внешнему виду логарифм от корня квадратного, а экспоненту – от параболы).

И после этого – учимся решать сами задачи №18 Профильного ЕГЭ.

Вот основные типы задач с параметрами:

Еще одна задача с параметром – повышенного уровня сложности. Автор задачи – Анна Малкова

И несколько полезных советов тем, кто решает задачи с параметрами:

1. Есть два универсальных правила для решения задач с параметрами. Помогают всегда. Хорошо, в 99% случаев помогают. То есть почти всегда.

— Если в задаче с параметром можно сделать замену переменной – сделайте замену переменной.

— Если задачу с параметром можно решить нарисовать – рисуйте. То есть применяйте графический метод.

2. Новость для тех, кто решил заниматься только алгеброй и обойтись без геометрии (мы уже рассказывали о том, почему это невозможно). Многие задачи с параметрами быстрее и проще решаются именно геометрическим способом.

Эксперты ЕГЭ очень не любят слова «Из рисунка видно…» Ваш рисунок – только иллюстрация к решению. Вам нужно объяснить, на что смотреть, и обосновать свои выводы. Примеры оформления – здесь. Эксперты ЕГЭ также не любят слова «очевидно, что…» (когда ничего не очевидно) и «ёжику ясно…».

3. Сколько надо решить задач, чтобы освоить тему «Параметры на ЕГЭ по математике»? – Хотя бы 50, и самых разных. И в результате, посмотрев на задачу с параметром, вы уже поймете, что с ней делать.

4. Задачи с параметрами похожи на конструктор. Разобрав много таких задач, вы заметите, как решение «собирается» из знакомых элементов. Сможете разглядеть уравнение окружности или отрезка. Переформулировать условие, чтобы сделать его проще.

На нашем Онлайн-курсе теме «Параметры» посвящено не менее 12 двухчасовых занятий. Кстати, оценивается задача 18 Профильного ЕГЭ в 4 первичных балла, которые отлично пересчитываются в тестовые!

Видео:Уравнения с параметрами | Алгебра 11 класс #32 | ИнфоурокСкачать

Уравнения с параметром — алгоритмы и примеры решения

Видео:✓ Система уравнений с параметром | ЕГЭ-2016. Задание 17. Математика. Профиль | Борис ТрушинСкачать

Общие сведения

Уравнением является любое математическое тождество или физический закон, в котором присутствуют неизвестные величины. Последние необходимо находить. Этот процесс называется поиском корней. Однако не во всех случаях у равенства с переменными бывают решения, а это также нужно доказать.

Корень — величина или диапазон, превращающие искомое выражение в верное равенство. Например, в 5s=10 переменная эквивалентна 2, поскольку только это значение позволяет получить верное тождество, то есть 5*2=10.

Примером диапазона или интервала решений является выражение следующего вида: 0/t=0. Его корнем может быть любое действительное число, кроме нуля. Записывается решение в таком виде: t ∈ (-inf;0)U (0;+inf), где «∈» — знак принадлежности, «-inf» и «inf» — минус и плюс бесконечно большие числа соответственно.

Параметром в уравнении называется некоторая величина, от которой зависит поведение равенства на определенном интервале. Следует отметить, что он также влияет на значение корня, когда входит с ним в различные арифметические операции: сложения, вычитания, умножения, деления, возведения в степень и так далее. Тождества такого типа называют также параметрическими. Далее необходимо разобрать классификацию уравнений.

Видео:Решаем квадратное уравнение с параметромСкачать

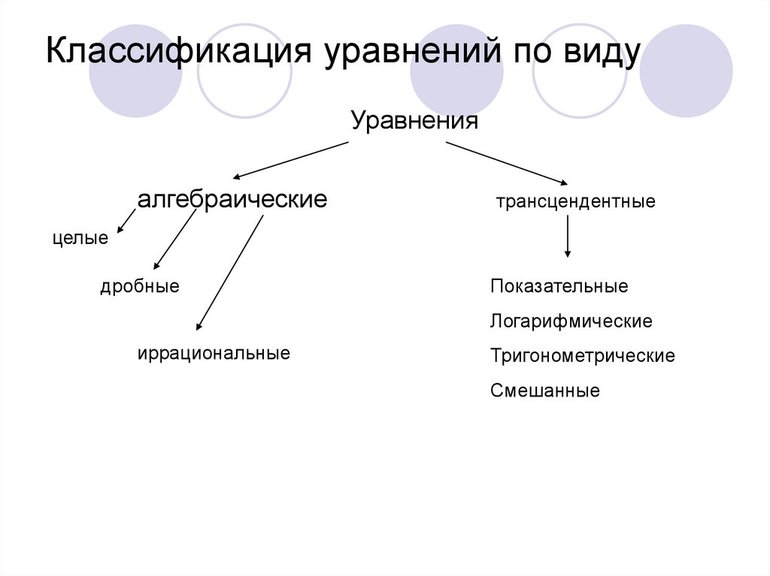
Классификация уравнений

Уравнения делятся на определенные виды, от которых зависит выбор методики их решения. Они бывают следующими: алгебраическими, дифференциальными, функциональными, трансцендентными и тригонометрическими. Кроме того, все они могут содержать некоторую величину — параметр. Его часто обозначают литерой «р» или «а».

Алгебраический тип является наиболее простым, поскольку не содержит сложные элементы. Дифференциальные тождества с неизвестными — одни из самых сложных выражений с точки зрения алгоритма. Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.

Практически все функциональные уравнения содержат один или более параметров. Основное их отличие от остальных заключается в функции, которая задается сложным выражением. Последнее может включать несколько неизвестных и параметрических элементов. Примером такого тождества является функция Лапласа, содержащая интеграл обыкновенного типа, а также экспоненту.

К трансцендентным относятся выражения, содержащие показательную, логарифмическую и радикальную (знак корня). Последний тип — тригонометрические. Они содержат любое равенство, содержащее следующие функции: sin, cos, tg и ctg. Однако в математике встречаются также их производные: arcsin, arccos, arcctg, arctg и гиперболические тождества.

Специалисты рекомендуют освоить на начальных этапах обучения методики, позволяющие решать уравнения с параметром линейного типа. После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.

Видео:5-часовой стрим по ПАРАМЕТРАМ. Вся алгебра для №17 с нуля и до уровня ЕГЭ 2023Скачать

Алгебраический вид

Алгебраические не содержат в своем составе сложных функций, но в них могут присутствовать компоненты со степенным показателем.

На основании последней характеристики они делятся на 5 типов:

1. Линейные.
2. Квадратные (квадратичные).
3. Кубические.
4. Биквадратные.
5. Высших порядков.

Линейные — выражения с переменной, которая имеет только первую степень (равную единице). Если показатель эквивалентен двойке, то такое тождество называется квадратным. В математической интерпретации его еще называют квадратным трехчленом. Когда показатель при неизвестной эквивалентен тройке, тогда это равенство называется кубическим.

Наиболее сложными по своей структуре являются биквадратные (содержат 4 степень). Однако на этом виды линейных уравнений не заканчиваются, поскольку бывают равенства с более высокими показателями. Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.

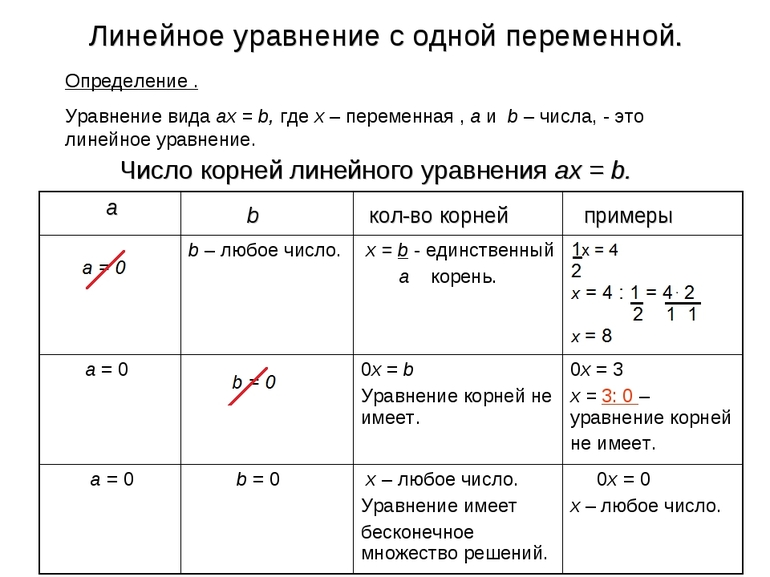
Линейные и квадратичные

Линейное — это самое простое уравнение, которое имеет всего одно решение. Оно решается по следующей методике:

1. Записывается искомое выражение.
2. При необходимости раскрываются скобки и приводятся подобные элементы.
3. Неизвестные (переменные) остаются в левой части тождества, а все константы (числа) — переносятся вправо.
4. Правая часть сокращается на коэффициент при неизвестной.
5. Записывается результат.
6. Выполняется проверка посредством подстановки корня в исходное выражение.

Следует отметить, что линейное выражение с переменной может не иметь решений, поскольку иногда невозможно выполнить операцию сокращения. Например, 0t=85. Равенство не имеет корней, поскольку на нулевое значение делить нельзя, так как при этом получается пустое множество.

Следующим типом является уравнение квадратичной формы At 2 +Bt+C=0. Оно может иметь один или два решения. Однако бывают случаи, при которых корней нет вообще. Для получения результата вводится понятие дискриминанта «D=(-B)^2−4*А*С». Для решения следует воспользоваться следующим алгоритмом:

1. Записать выражение.
2. Выполнить при необходимости математические преобразования по раскрытию скобок и приведению подобных слагаемых.
3. Вычислить значение D (D 0 — два решения).
4. При D=0 формула корня имеет такой вид: t=-В/(2А).
5. Если D>0, то решения определяются по следующим соотношениям: t1=[-В-D^(½)]/(2А) и t2=[-В+D^(½)]/(2А).
6. Записать результат.
7. Выполнить проверку по отсеиванию ложных корней.

Следует отметить, что ложный корень — значение переменной, полученное по соответствующей формуле, но при подстановке в исходное выражение не выполняет условие равенства нулевому значению.

Кроме того, нужно обратить внимание на типы квадратных уравнений. Они бывают полными и неполными. Первые содержат все коэффициенты (А, В и С), а во вторых — некоторые из них могут отсутствовать, кроме А, так как тогда тождество должно содержать вторую степень при неизвестной.

Неполные решаются методом разложения на множители. Например, «v 2 −81=0» раскладывается следующим образом (формула сокращенного умножения — разность квадратов): (v-9)(t+9)=0. Анализируя последнее равенство, можно сделать вывод о понижении степени. Корнями уравнения являются два значения, t1=-9 и t2=9.

Кубичеcкие и биквадрaтные

Кубические и биквадратные равенства с неизвестным рекомендуется решать при помощи замены переменной. Однако в некоторых случаях можно применить формулы понижения степени или разложения на множители. Иными словами, суть решения алгебраических уравнений, степень которых превышает двойку, сводится к ее понижению различными методами.

Замена переменной производится на другую неизвестную величину. В примере (t 3 −2)+2t 3 −4=0 можно ввести следующий элемент — v=t 3 −2. В результате этого получится равенство такого вида: v+2v=0. Оно решается очень просто:

1. Приводятся подобные элементы: 3v=0.
2. Находится корень: v=0.
3. Приравнивается к выражению, которое заменяли: t 3 −2=0.
4. Находится корень (один, поскольку у радикала нечетная степень): t=[2]^(1/3).
5. Проверяется условие: 2^(1/3)^3−2+2*(2^(1/3)^3)-4=4−4=0 (истина).

Биквадратные тождества решаются таким же методом. Однако существует еще один способ — разложение на множители. Его необходимо разобрать на примере решения выражения «4m 4 −324=0». Решать нужно по такому алгоритму:

1. Упростить (вынести четверку за скобки и сократить на нее): 4 (m 4 −81)=m 4 −81=0.
2. Разложить на множители (разность квадратов): (m 2 −9)(m 2 +9)=(m-3)(m+3)(m 2 +9)=0/
3. Решить три уравнения: m1=3, m2=-3, m3=-3 и m4=3.
4. Результат: m1=-3 и m2=3.
5. Проверка: 4*(-3)^4−324=0 (истинно) и 4*(3)^4−324=0 (истинно).

Каждый из методов решения выбирается в зависимости от самого уравнения. При чтении условия задачи необходимо определить способ решения. Последний должен быть простым и удобным, а главное — количество шагов решения должно быть минимальным, что существенно сказывается на затраченном времени при вычислениях. Далее нужно рассмотреть подробный алгоритм решения уравнения с параметром.

Видео:✓ Пять способов решить задачу с параметром | ЕГЭ-2018. Задание 17. Математика | Борис ТрушинСкачать

Пример решения

На основании изученного материала можно приступить к практике решения уравнения с параметром, которое имеет следующий вид: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4, где р — некоторый параметр. Корни и величину р необходимо искать по следующему алгоритму:

1. Записать равенство с неизвестным и параметром: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4.
2. Выполнить математические преобразования: 2v 4 −32−4p-v 2 +4+v 2 −4-v 4 +16+4=v 4 −16+4p+4=0.
3. Ввести замену v 4 −16=m: m+4p+4=0.
4. Вывести формулу нахождения параметра: р=-(m/4)-1.
5. Подставить величину m: р=-1-(v 4 +16)/4.
6. C учетом соотношения равенство будет иметь такой вид: v 4 −16+4[-(v 4 +16−4)/4]+4=-32+8=0 (корней нет, поскольку -24 4 −12=0.
7. Корни: v1=[12]^(¼) и v2=-[12]^(¼).
8. Отрицательного корня v2 не существует, поскольку показатель радикала — четное число.
9. Результат: v1=[12]^(¼).
10. Проверка: ^4−16+4=16−16=0 (истина).

Следует отметить, что v2 — ложный корень, а также параметр p, равный какому-либо значению, превращает уравнение в пустое множество. Для проверки можно воспользоваться специальным приложением, которое называется онлайн-калькулятором.

Таким образом, уравнения с параметром являются наиболее сложными, поскольку необходимо искать их корни, а также некоторое значение, влияющее на логику выражения. Для их решения необходимо следовать специальному алгоритму, предложенному математиками.

🎥 Видео

Решить квадратное уравнение с параметром - bezbotvyСкачать

Алгебра 8 класс (Урок№33 - Уравнения с параметром. Контрольный урок.)Скачать