Однородные и неоднородные волновые уравнения для векторов ЭМП. Уравнения Даламбера. Решение однородных уравнений Даламбера. Сферическая волна. Волновой фронт. Волновые уравнения Гельмгольца.
Плоские волны как частные решения волновых уравнений. Плоская волна как предельный случай сферической волны. Решения волновых уравнений для гармонических полей в виде плоских и сферических волн.
Плоские ЭМВ в однородной изотропной среде. Отличие понятий «волна» и «колебание». Свойства плоской волны, структура и ориентация векторов ЭМП. Коэффициенты фазы и ослабления. Длина волны. Фазовая скорость, скорость распространения энергии, групповая скорость.
Характеристическое и волновое сопротивления. Ослабление ЭМВ, глубина проникновения ЭМП в вещество.
Указания к теме
Решением волновых уравнений являются функции координат и времени, которые описывают ЭМВ, распространяющиеся в свободном пространстве, направляющих системах и других устройствах. Необходимо получить четкое представление о таких понятиях, как фазовая поверхность (волновой фронт) и ее форма, однородная и неоднородная волна, затухающая волна.
Следует выучить определения длины волны, коэффициентов затухания и фазы, групповой и фазовой скоростей, волнового и характеристического сопротивлений, глубины проникновения ЭМВ в вещество.
Основные сведения
Для анализа распространяющихся ЭМВ из системы уравнений Максвелла в дифференциальной форме целесообразно вывести уравнения, которые зависят либо только от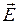 
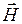
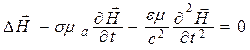
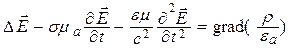
, либо только от 
. Если параметры среды (s, e, m) не зависят от координат и времени, то после преобразований получим [1–6]
; (5.1)
. (5.2)
Как показали расчеты и эксперименты, константа с (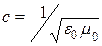 
) для ЭМП удивительным образом совпадает со значением скорости света в вакууме. Из этого был сделан вывод о том, что ЭМВ и свет имеют одну и ту же природу. В пространстве без потерь ЭМВ распространяются со скоростью света.
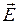
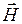
Уравнения (5.1) и (5.2) называют волновыми уравнениями Ж. Д’Аламбера [5, 12]. Если правая часть равна нулю, то уравнение называют однородным, а если нет – неоднородным. При отсутствии электрических зарядов (r = 0) уравнения (5.1) и (5.2) практически совпадают, что подтверждает равноправие векторов и у распространяющегося в пространстве ЭМП.
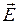
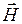
Несмотря на кажущуюся независимость уравнений (5.1) и (5.2), следует помнить о том, что у переменного ЭМП векторы и связаны уравнениями Максвелла и не могут существовать друг без друга.
Волновые уравнения в комплексной форме имеют вид
; 
, (5.3)
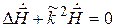
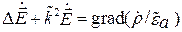
где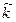 
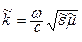
– волновое число:
. (5.4)
Уравнения (5.3) называют волновыми уравнениями Г. Гельмгольца. При отсутствии потерь проводимости (s = 0) исчезают вторые слагаемые в уравнениях (5.1) и (5.2), а также в (5.3)–(5.4) возможно упрощение:
.
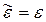
Рассмотренные уравнения называются волновыми потому, что их решениями являются волны и, в частности, ЭМВ.
Фазовым фронтом волны называют поверхность, проходящую через точки с одинаковыми фазами, по форме этой поверхности определяется название волны (сфера – сферическая ЭМВ, плоскость – плоская и т. д.) [1–3].
Решение однородного волнового уравнения для плоских волн
. (5.5)
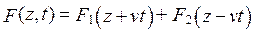
Каждое из слагаемых выражения (5.5) описывает возмущения F1 и F2, исходящие из точки z0 в момент t = 0 и к моменту времени t приходящие в точку z = z0 – vt для F1 и в точку z = z0 + vt для F2 со скоростью v [1].
Для сферических волн решение волнового уравнения имеет вид:
. (5.6)
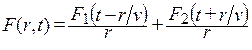
Первое слагаемое выражения (5.6) представляет собой сферическую волну, расходящуюся от источника. Второе слагаемое часто отбрасывают, поскольку волна, движущаяся внутрь источника, обычно не рассматривается [1].
В отличие от выражения (5.5) амплитуда сферической волны (5.6) уменьшается при удалении от источника как 1/r (мощность – как 1/r 2 ), что связано с тем, что мощность изотропного источника распределяется по расходящимся сферам (4.10).
Таким образом, даже при отсутствии потерь в пространстве плотность потока мощности сферической волны уменьшается с расстоянием как 1/r 2 .
На большом расстоянии от источника ЭМВ (в дальней зоне антенны) сферический волновой фронт в области приемной антенны можно аппроксимировать плоскостью, подобно тому, как земную поверхность считают плоской при малых высотах и на дистанциях, много меньших расстояния прямой видимости.
Плоская ЭМВ – идеализированная волна, имеющая плоский фазовый фронт (z = const), у которой существуют две взаимно перпендикулярные составляющие 
и 
, зависящие только от координаты z и расположенные в плоскости, перпендикулярной z. ЭМВ называется однородной, если ее амплитуда постоянна во всех точках фазового фронта, и неоднородной, если ее амплитуда зависит от координат точек фазового фронта.
В дальнейшем будем считать, что направление распространения ЭМВ совпадает с осью z. Уравнения Максвелла в комплексной форме для составляющих векторов плоской волны в ДСК имеют вид
; 
; 
; 
. (5.7)
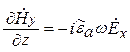
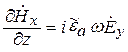
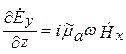
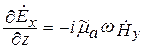
Из формул (5.7) следует, что и взаимно перпендикулярны. (Это можно доказать, рассмотрев скалярное произведение векторов [11].) В дальнейшем будем обозначать координаты этих векторов 
и 
, подчеркивая их поперечную направленность и расположение в плоскости x0y.
Зная или , можно легко найти другую поперечную составляющую и перейти к обычным координатам ( 
, 
, 
, 
).
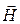
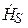
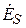
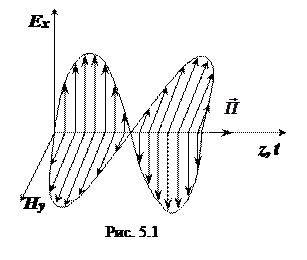
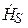
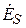
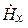
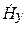
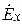
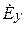
Вектор Пойнтинга в данном случае имеет только продольную составляющую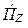 
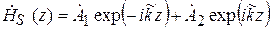
(рис. 5.1). Решение уравнений (5.3) имеет вид
. (5.8)
Первое слагаемое выражения (5.8) соответствует прямой волне, второе слагаемое – обратная волна,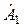 
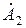
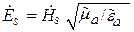
и 
– комплексные амплитуды данных бегущих волн (для – аналогично). Подставляя выражение (5.8) в (5.7), получим
. (5.9)
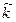
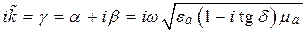
Запишем связь волнового числа ( ) с комплексным коэффициентом распространения (g) для среды без магнитных потерь :
, (5.10)
Уравнение плоской волны с учетом (5.10) можно записать в виде
. (5.11)
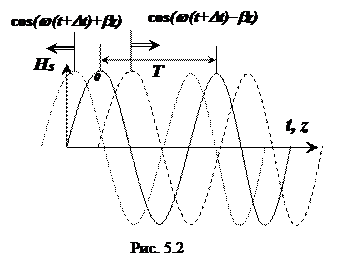
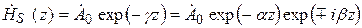
Для мгновенных значений из выражения (5.11) получаем
. (5.12)
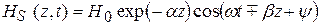
Направление распространения ЭМВ можно определить из анализа зависимости полной фазы (5.12)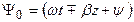 
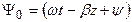
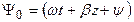
от времени. Зафиксировав волновой фронт в какой-то момент времени, получаем, что если 
, то в следующий момент времени ЭМВ сместится в положительном направлении оси z, а при 
волновой фронт будет двигаться в отрицательном направлении оси z(рис. 5.2) [1].
Из анализа формул (5.10)–(5.12) очевидно, что a– это коэффициент затухания, а b – коэффициент фазы.
Подставляя формулу (5.12) в (5.1), после решения уравнений относительно a и b получаем
, (5.13)
. (5.14)
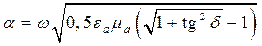
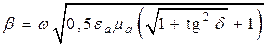
Множитель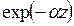 
в выражениях (5.10)–(5.12) показывает затухание при распространении ЭМВ вдоль оси z. Чем больше a, тем больше затухание.
Ослаблением (A) ЭМВ по полю называют величину (AP = A 2 – ослабление ЭМВ по мощности)
, 
. (5.15)
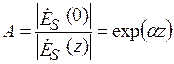
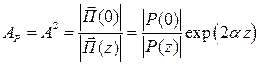
На практике часто используют ослабление в децибелах (дБ):
. (5.16)
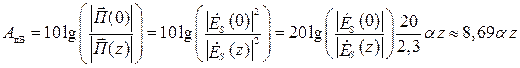
С ослаблением непосредственно связана глубина проникновения ЭМП в вещество (D° ), называемая также толщиной поверхностного слоя (скин-слоя, но это понятие логичнее использовать для металлов):
. (5.17)
При прохождении слоя вещества z =D° амплитуда ЭМП ослабляется в е (е = 2,718…) раз, и соответственно в следующий слой (рис. 5.3) проходит лишь 1/е 2 мощности ЭМП. Получается, что в поверхностном слое D° концентрируется 86,5% энергии ЭМП, в слое 2D° – 98,2%,а в слое 3D° – 99,8%.
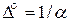
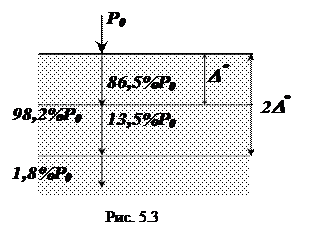
Таким образом, зная коэффициент затухания, можно определить область преимущественной концентрации энергии ЭМВ в веществе.
В случае диэлектриков толщина поверхностного слоя значительна, в то время как для проводников на ВЧ и ОВЧ она составляет доли миллиметра [1].
Параметры ЭМВ. Длиной волны l называется расстояние между двумя фронтами ЭМВ, различающимися по фазе на 2p (360°):
. (5.18)
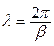
Фазовой скоростью vф называется скорость перемещения фазового (волнового) фронта ЭМВ. При анализе выражения (5.12) ранее были определены направление движения и скорость фронта ЭМВ
. (5.19)
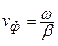
Фазовая скорость может изменяться в любых пределах (может быть больше с!), поскольку не является скоростью переноса энергии [1].
Групповой скоростью vгр называют скорость движения фронта (например, максимума) огибающеймодулированного сигнала.
Информационный сигнал не является монохроматическим, он занимает полосу частот. Каждая спектральная составляющая может иметь свою скорость распространения, что в диспергирующих средах приводит к искажениям сигнала.
Понятие «групповая скорость» вводится для сред с малыми потерями, поэтому при Dw vф (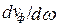 
>0).
При Dw/w0 ® 0 период огибающей стремится в бесконечность, понятие «группа волн» распространяется на весь сигнал, и в итогеvгр ® vЭ.
Групповая скорость узкополосного сигнала – это скорость передачи энергии, она не может быть выше скорости света.
Характеристическое сопротивление (Zс) [41] ЭМВ равно отношению амплитуд поперечных составляющих электрического и магнитного полей
. (5.21)
При комплексном Zс отстает или опережает по фазе вектор на некоторый угол. На рис. 5.5 вектор опережает на 90° (π/4), а на рис. 5.1 данные векторы синфазны.
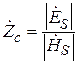
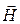
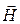
Определим характеристическое сопротивление плоской волны. Пусть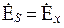 
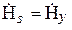
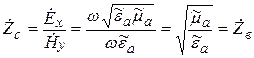
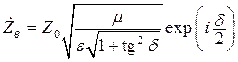
, а 
, тогда из формул (5.7) следует:
, 
. (5.22)
Получается, что характеристическое сопротивление [41]зависит только от параметров среды. Zв называют волновым сопротивлением среды. Следует отметить, что стандартом [41] рекомендуется термин «характеристическое сопротивление». Для ЭМВ, распространяющейся в некоторой среде, Zc = Zв.
Волновое сопротивление вакуума Z0 (s = 0, e = m = 1) :
377,0 Ом. (5.23)
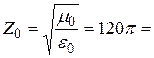
Тогда выражение (5.22) можно записать в виде
. (5.24)
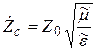
Список рекомендуемой литературы:[1, гл. 6–7, с. 30–38; 2, с. 50–56; 3, гл. 6–7, с. 27–34; 4, с. 26–33; 5, с. 26–30; 6, с. 116–123, 128–142, 198–205; 7, с. 67–82, 250–259; 8, с. 62–68; 9, с. 69–74; 10, с. 68–73; 11, с. 67–69, 130–139; 12, с. 182–194; 13, с. 140–149, 174–177, 187–190; 15, с. 302–307].
Контрольные вопросы и задания
1. Почему рассматриваемые в этой теме уравнения называются волновыми?
2. Чем волна отличается от колебания?
3. Чем отличаются волновые уравнения Д’Аламбера и Гельмгольца?
4. Следует ли из волновых уравнений независимость электрической и магнитной составляющих ЭМП?
5. Можно ли считать свет ЭМ волной?
6. Какие упрощения возможны в волновых уравнениях для сред без потерь?
7. Можно ли по виду электрической или магнитной составляющей плоской ЭМВ определить расположение другой составляющей ЭМП и направление распространения ЭМВ?
8. При каких условиях волновые уравнения для векторов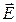 
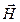
и 
идентичны?
9. Каково простейшее решение системы уравнений Максвелла?
10. Дайте определение волнового фронта.
11. Почему плотность потока энергии сферической волны уменьшается при удалении от источника даже в пространстве без потерь?
12. Какие упрощения в анализе ЭМП дает понятие «плоская волна»? В каких практических случаях допустимо ЭМВ считать плоской?
13. Чем отличаются однородные и неоднородные плоские волны?
14. Дайте определение коэффициентам затухания и фазы плоской ЭМВ.
15. Чем отличается волновое число k от g ?
16. Какова пространственная структура плоской ЭМВ?
17. Как определить направление распространения ЭМВ?
18. Как с помощью понятия толщины поверхностного слоя можно оценить область преимущественной концентрации ЭМП?
19. Дайте определение основным характеристикам ЭМВ.
20. Чем групповая скорость отличается от фазовой?
21. Может ли фазовая скорость иметь бесконечное значение?
22. Чем волновое сопротивление отличается от характеристического?
23. Является ли групповая скорость скоростью передачи энергии?
24. Что такое дисперсия? Приведите примеры дисперсионных сред.
25. Укажите условие неискаженной передачи сигнала.
26. Чем нормальная дисперсия отличается от аномальной?
Видео:Билеты №32, 33 "Уравнения Максвелла"Скачать
2.6. Электромагнитные волны
Любой колебательный контур излучает энергию. Изменяющееся электрическое поле возбуждает в окружающем пространстве переменное магнитное поле, и наоборот. Математические уравнения, описывающие связь магнитного и электрического полей, были выведены Максвеллом и носят его имя. Запишем уравнения Максвелла в дифференциальной форме для случая, когда отсутствуют электрические заряды (
) и токи (j = 0):
Величины 
и 
— электрическая и магнитная постоянные, соответственно, которые связаны со скоростью света в вакууме соотношением
Постоянные 
и 
характеризуют электрические и магнитные свойства среды, которую мы будем считать однородной и изотропной.
В отсутствие зарядов и токов невозможно существование статических электрического и магнитного полей. Однако переменное электрическое поле возбуждает магнитное поле, и наоборот, переменное магнитное поле создает электрическое поле. Поэтому имеются решения уравнений Максвелла в вакууме, в отсутствие зарядов и токов, где электрические и магнитные поля оказываются неразрывно связанными друг с другом. В теории Максвелла впервые были объединены два фундаментальных взаимодействия, ранее считавшихся независимыми. Поэтому мы говорим теперь об электромагнитном поле.
Колебательный процесс в контуре сопровождается изменением окружающего его поля. Изменения, происходящие в окружающем пространстве, распространяются от точки к точке с определенной скоростью, то есть колебательный контур излучает в окружающее его пространство энергию электромагнитного поля.
Электромагнитная волна — это распространяющееся в пространстве электромагнитное поле, в котором напряженность электрического и индукция магнитного полей изменяются по периодическому закону.
При строго гармоническом изменении во времени векторов 
и 
электромагнитная волна называется монохроматической.
Получим из уравнений Максвелла волновые уравнения для векторов и .
Волновое уравнение для электромагнитных волн
Как уже отмечалось в предыдущей части курса, ротор (rot) и дивергенция (div) — это некоторые операции дифференцирования, производимые по определенным правилам над векторами. Ниже мы познакомимся с ними поближе.
Возьмем ротор от обеих частей уравнения
При этом воспользуемся доказываемой в курсе математики формулой:
где 
— введенный выше лапласиан. Первое слагаемое в правой части равно нулю в силу другого уравнения Максвелла:
Получаем в итоге:
Выразим rotB через электрическое поле с помощью уравнения Максвелла:
и используем это выражение в правой части (2.93). В результате приходим к уравнению:
и вводя показатель преломления среды
запишем уравнение для вектора напряженности электрического поля в виде:
Сравнивая с (2.69), убеждаемся, что мы получили волновое уравнение, где v — фазовая скорость света в среде:
Взяв ротор от обеих частей уравнения Максвелла
и действуя аналогичным образом, придем к волновому уравнению для магнитного поля:
Полученные волновые уравнения для 
и 
означают, что электромагнитное поле может существовать в виде электромагнитных волн, фазовая скорость которых равна
В отсутствие среды (при 
) скорость электромагнитных волн совпадает со скоростью света в вакууме.
Основные свойства электромагнитных волн
Рассмотрим плоскую монохроматическую электромагнитную волну, распространяющуюся вдоль оси х:
Возможность существования таких решений следует из полученных волновых уравнений. Однако напряженности электрического и магнитного полей не являются независимыми друг от друга. Связь между ними можно установить, подставляя решения (2.99) в уравнения Максвелла. Дифференциальную операцию rot, применяемую к некоторому векторному полю А можно символически записать как детерминант:
Подставляя сюда выражения (2.99), зависящие только от координаты x, находим:
Дифференцирование плоских волн по времени дает:
Тогда из уравнений Максвелла следует:
Отсюда следует, во-первых, что электрическое и магнитное поля колеблются в фазе:
Далее, ни у 
, ни у 
нет компонент параллельных оси х:
Иными словами и в изотропной среде,
электромагнитные волны поперечны: колебания векторов электрического и магнитного полей происходят в плоскости, ортогональной направлению распространения волны.
Тогда можно выбрать координатные оси так, чтобы вектор 
был направлен вдоль оси у (рис. 2.27):
Рис. 2.27. Колебания электрического и магнитного полей в плоской электромагнитной волне
В этом случае уравнения (2.103) приобретают вид:
Отсюда следует, что вектор 
направлен вдоль оси z:
Иначе говоря, векторы электрического и магнитного поля ортогональны друг другу и оба — направлению распространения волны. С учетом этого факта уравнения (2.104) еще более упрощаются:
Отсюда вытекает обычная связь волнового вектора, частоты и скорости:
а также связь амплитуд колебаний полей:
Отметим, что связь (2.107) имеет место не только для максимальных значений (амплитуд) модулей векторов напряженности электрического и магнитного поля волны, но и для текущих — в любой момент времени.
Итак, из уравнений Максвелла следует, что электромагнитные волны распространяются в вакууме со скоростью света. В свое время этот вывод произвел огромное впечатление. Стало ясно, что не только электричество и магнетизм являются разными проявлениями одного и того же взаимодействия. Все световые явления, оптика, также стали предметом теории электромагнетизма. Различия в восприятии человеком электромагнитных волн связаны с их частотой или длиной волны.
Шкала электромагнитных волн представляет собой непрерывную последовательность частот (и длин волн) электромагнитного излучения. Теория электромагнитных волн Максвелла позволяет установить, что в природе существуют электромагнитные волны различных длин, образованные различными вибраторами (источниками). В зависимости от способов получения электромагнитных волн их разделяют на несколько диапазонов частот (или длин волн).
На рис. 2.28 представлена шкала электромагнитных волн.
Рис. 2.28. Шкала электромагнитных волн
Видно, что диапазоны волн различных типов перекрывают друг друга. Следовательно, волны таких длин можно получить различными способами. Принципиальных различий между ними нет, поскольку все они являются электромагнитными волнами, порожденными колеблющимися заряженными частицами.
Уравнения Максвелла приводят также к выводу о поперечности электромагнитных волн в вакууме (и в изотропной среде): векторы напряженности электрического и магнитного полей ортогональны друг другу и направлению распространения волны.
http://www.femto.com.ua/articles/part_1/0560.html – Волновое уравнение. Материал из Физической Энциклопедии.
http://elementy.ru/trefil/24 – Уравнения Максвелла. Материал из «Элементов».
http://telecomclub.org/?q=node/1750 – Уравнения Максвелла и их физический смысл.
http://principact.ru/content/view/188/115/ – Кратко об уравнениях максвелла для электромагнитного поля.
Эффект Доплера для электромагнитных волн
Пусть в некоторой инерциальной системе отсчета К распространяется плоская электромагнитная волна. Фаза волны имеет вид:
Наблюдатель в другой инерциальной системе отсчета К’, движущейся относительно первой со скоростью V вдоль оси x, также наблюдает эту волну, но пользуется другими координатами и временем: t’, r’. Связь между системами отсчета дается преобразованиями Лоренца:
Подставим эти выражения в выражение для фазы 
, чтобы получить фазу 
волны в движущейся системе отсчета:
Это выражение можно записать как
где 
и 
— циклическая частота и волновой вектор относительно движущейся системы отсчета. Сравнивая с (2.110), находим преобразования Лоренца для частоты и волнового вектора:
Для электромагнитной волны в вакууме
Пусть направление распространения волны составляет в первой системе отсчета угол 
с осью х:
Тогда выражение для частоты волны в движущейся системе отсчета принимает вид:
Это и есть формула Доплера для электромагнитных волн.
Если 
, то наблюдатель удаляется от источника излучения и воспринимаемая им частота волны уменьшается:
Если 
, то наблюдатель приближается к источнику и частота излучения для него увеличивается:
При скоростях V 2 (солнечная постоянная). Найдем среднюю амплитуду колебаний E0 вектора электрической напряженности в солнечном излучении. Вычислим амплитуды колебаний напряженности магнитного поля H0 и вектора магнитной индукции B0 в волне.
Ответ находим сразу из уравнений (3.127), где полагаем 
:
Электромагнитные волны поглощаются и отражаются телами, следовательно, они должны оказывать на тела давление. Рассмотрим плоскую электромагнитную волну, падающую нормально на плоскую проводящую поверхность. В этом случае электрическое поле волны возбуждает в теле ток, пропорциональный Е. Магнитное поле волны по закону Ампера будет действовать на ток с силой, направление которой совпадает с направлением распространения волны. В 1899 г. в исключительно тонких экспериментах П.И. Лебедев доказал существование светового давления. Можно показать, что волна, несущая энергию W, обладает и импульсом:
Пусть электромагнитная волна падает в вакууме по нормали на площадь А и полностью поглощается ею. Предположим, что за время 
площадка получила от волны энергию 
. Тогда переданный площадке импульс равен
На площадку действует со стороны волны сила
Давление Р, оказываемое волной, равно
Если средняя плотность энергии в волне равна , то на площадь А за время 
попадет энергия из объема 
и
Отсюда находим давление электромагнитной волны (света):
Если площадка идеально отражает всю падающую на нее энергию, то давление будет в два раза большим, что объясняется очень просто: одинаковый вклад в давление в этом случае дают как падающая, так и отраженная волны, в случае полностью поглощающей поверхности отраженной волны просто нет.
Пример 3. Найдем давление Р солнечного света на Землю. Используем значение солнечной постоянной из предыдущего примера. Искомое давление равно:
Пример 4. Найдем давление Р лазерного пучка на поглощающую мишень. Выходная мощность лазера N = 4.6 Вт, диаметр пучка d = 2.6 мм.
Видео:Билет №34 "Электромагнитные волны"Скачать
Волновое уравнение. Электромагнитные волны
Вы будете перенаправлены на Автор24
Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать
Общая форма записи волнового процесса
Допустим, что физическая величина $s$ распространяется в направлении $X$ со скоростью $v$. Данная величина ($s$) может быть смещением, скоростью кусочков резинового шнура, когда в шнуре проходит механическая волна. Если мы имеем дело с электромагнитной волной, то под $s$ можно понимать напряженность электрического поля или индукцию магнитного поля и т.д. Общая форма записи волнового процесса представляется как:
где $t$ — время, $x$ — координата точки, которую рассматривают, $f$ — символ функции.
Любая произвольная функция, имеющая исключительно аргумент $left(t-fracright)$, отражает волновой процесс.
Положим, что наблюдатель перемещается по $оси X$ со скоростью $v$. Его координата может быть определена как:
Подставим правую часть выражения (2) в формулу (1) вместо переменной $x$, получим:
Из выражения (3) следует, что функция $fleft(-fracright)$ не зависит от времени, что означает $s$ распространяется со скоростью $v$.
Аналогично можно получить, что если процесс записан как:
то $s$ распространяется против избранной $оси X$. Если положить, что $t=0$, то из выражений (1) и (4) имеем:
Выражение (5) определяет распределение $s$ в начальный момент времени. В том случае, если $s$ напряженность магнитного поля в электромагнитной волне, то формула (5) — задает распределение магнитного поля в пространстве при $t=0$. Получается, что вид функции $f$ зависит от начальных условий процесса.
Итак, выражения (1) и (4) являются общим выражением для волны, которая распространяется вдоль $оси X$.
Видео:*** Лекция. Волновое уравнение электромагнитной волны ******Скачать
Волновое уравнение
Функция $s$ удовлетворяет простому дифференциальному уравнению. Для его нахождения продифференцируем выражения (1) и (4), объединив их, используя знак $mp $, дважды по координате $x$:
Вторая частная производная по времени будет иметь вид:
Используя выражения (6) и (7) запишем:
Уравнение (8) называют волновым. В том случае, если волна распространяется не в одном, во всех направлениях пространства, то волновое уравнение примет вид:
Готовые работы на аналогичную тему
В том случае, если физическая величина распространяется в виде волны, то она должна удовлетворять волновому уравнению. Справедливо обратное утверждение: Если какая — либо величина подчиняется волновому уравнению, то она распространяется как волна. Скорость распространения волны будет равна квадратному корню из коэффициента, который стоит при сумме пространственных производных.
Видео:Раскрытие тайн электромагнитной волныСкачать
Электромагнитные волны
Рассмотрим электромагнитное поле в однородном диэлектрике ($j_x=j_y=j_z=0$). Причем будем считать задачу одномерной, то есть предположим, что векторы $overrightarrow и overrightarrow$ зависят только от одной координаты $x$ и времени $t$. Такая ситуация означает, что все пространство мы можем разделить на тонике слои (толщина слоя стремится к нулю), плоские слои, внутри них $overrightarrow и overrightarrow$ принимают одно и тоже значение во всех точках. Данная задача соответствует плоской электромагнитной волне. Для описания электромагнитного поля используем систему уравнений Максвелла:
Для одномерного случая система уравнений Максвелла существенно упрощается, так как все производные по $y$ и $z$ равны нулю. Записав уравнение (10) в скалярном представлении:
Становится очевидным, что в однородной среде для одномерного случая:
Аналогично из уравнения (11) получаем, что:
Выражения (15) и (16) означают, что данные составляющие электромагнитного поля не зависят от времени. А из уравнений (12) и (13) следует, что $D_x$и $B_x$ — не зависят от координаты. В результате мы имеем, что $D_x=const, B_x=const$.
Остальные уравнения из группы (14) примут вид:
От группы уравнений в скалярной форме, которые представляют выражение (11), остаются:
Уравнения (17) и (18) сгруппируем как две независимые части. Первая — связывающая $y$-составляющую электрического поля и $z$-составляющую магнитного поля:
Вторая часть связывает $z$-компоненту электрического поля и $y$-компоненту магнитного поля:
Получается, что переменное (во времени) электрическое поле ($D_y$) порождает одну $z$-составляющую магнитного поля ($H_z$), переменное магнитное поле $B_z$ вызывает появление электрического поля направленного по $оси Y$ ($E_y$) (уравнения 19). То есть в электромагнитном поле электрическое и магнитные поля перпендикулярны друг другу. Аналогичный вывод можно сделать из пары (20).
Для одномерного случая систему уравнений Максвелла можно записать в виде:
Электрическое и магнитные поля могут существовать как волны, так как из уравнения Максвелла следует существование этих волн. Так как для напряженности электрического поля выполняется уравнение вида:
Следовательно, решение этого уравнения можно представить как:
Так как для напряженности магнитного поля выполняется уравнение вида:
следовательно, решение этого уравнения можно представить как:
Задание: Покажите, на примере одномерного случая электромагнитного поля, что из уравнений Максвелла следует волновой характер электромагнитного поля.
Решение:
В качестве основы для решения задачи используем уравнения Максвелла для одномерного случая:
Исключим из уравнений (1.1) магнитное поле $H$. С этой целью умножим первое уравнение на $mu _0$ и возьмем частную производную по времени от обеих частей равенства и, используя выражение: $D=varepsilon_0varepsilon E$, заменим электрическую индукцию на напряженность соответствующего поля, получим:
Второе уравнение в группе (1.1) продифференцируем по $x$, заменим индукцию магнитного поля на его напряженность, используя выражение: $B=mu _0H$, при этом имеем:
Как мы видим, правые части выражений (1.2) и (1.3) одинаковы, следовательно, можно считать, что:
Аналогичное уравнение легко получить для напряженности магнитного поля, если исключить напряженность электрического поля. Уравнение (1.4) — есть волновое уравнение.
Ответ: Волновое уравнение для напряженности электрической составляющей электромагнитного поля получено непосредственно из уравнений Максвелла для одномерной задачи.
Задание: Чему равна скорость ($v$) распространения электромагнитной волны?
Решение:
За основу решения примем волновое уравнение для напряженности электрического поля в плоской электромагнитной волне:
Скоростью распространения волны является корень квадратный из коэффициента, который находится перед $frac<^2E>$ в волновом уравнении, следовательно:
где $c$ — скорость распространения света в вакууме.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 02 03 2021
📹 Видео
4.2 Решение волновых уравнений Гельмгольца в виде плоских бегущих волнСкачать
Вывод волнового уравненияСкачать
Вывод уравнения электромагнитной волныСкачать
Урок 384. Излучение электромагнитных волн.Скачать
ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать
6. Кватернионное волновое уравнение первого порядка для электромагнитного поляСкачать
Электромагнитные волны. 11 класс.Скачать
О чем говорят уравнения Максвелла? Видео 1/2Скачать
Вывод волнового уравненияСкачать
Численное решение волнового уравнения (2)Скачать
5. Решение волнового уравнения на отрезке методом ФурьеСкачать
Численное решение волнового уравненияСкачать
Электромагнитное поле. Видеоурок по физике 11 классСкачать
Физика 9 класс (Урок№23 - Электромагнитное поле.)Скачать
Энергия электромагнитных волн. 11 класс.Скачать
