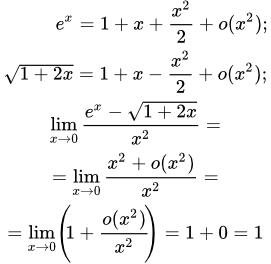Решение уравнения в виде ряда тейлора (4 видео)

Разложение функции в ряд Тейлора

Онлайн калькулятор для разложения функции в ряд Тейлора.
Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.
Ряд Тейлора был известен задолго до публикаций Тейлора — его использовали ещё в XVII веке Грегори, а также Ньютон.
Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.

Данный калькулятор предназначен для разложения функции в ряд Тейлора онлайн.

Разложение Тейлора задается единственной формулой для функций, которые раскладывается в степенной ряд по степеням (x-a) в определенном интервале. Разложение ряда Тейлора по степеням x (при a=0) является частным случаем и называется разложением Маклорена.

Калькулятор поможет разложить функцию в ряд Тейлора онлайн. Для того чтобы получить решение, необходимо ввести соответствующие значения в ячейки: вид функции, значение x и степень, до которой нужно разложить ряд.

Основные функции

: x^a

Содержание

Решение пределов, используя ряд Тейлора
Метод решения
Применяемые свойства о малого
Разложение элементарных функций в ряд Тейлора (Маклорена)
Примеры
Пример 1
Пример 2
Пример 3
Пример 4
Пример 5
Ряд Тейлора
Понятие ряда Тейлора.
Остаточный член формулы Тейлора.
Разложение элементарных функций в ряд Тейлора.
Разложение показательной и гиперболической функций в ряд Тейлора.
Разложение тригонометрических функций в ряд Тейлора.
Разложение логарифмической функции в ряд Тейлора.
Элементарные функции комплексного переменного.
🎥 Видео

Видео:Формула Тейлора за 3 минуты - bezbotvyСкачать

Решение пределов, используя ряд Тейлора

Видео:301 Нахождение решения дифференци ального уравнения в виде степенного рядаСкачать

Метод решения

Одним из самых мощных методов раскрытия неопределенностей и вычисления пределов является разложение функций в степенной ряд Тейлора. Применение этого метода состоит из следующих шагов.
1) Приводим неопределенность к виду 0/0 при переменной x , стремящейся к нулю. Для этого, если требуется, выполняем преобразования и делаем замену переменной.
2) Раскладываем числитель и знаменатель в ряд Тейлора в окрестности точки x = 0 . При этом выполняем разложение до такой степени x n , которая необходима для устранения неопределенности. Остальные члены включаем в o ( x n ) .

Этот метод применим, если после выполнения пункта 1), функции в числителе и знаменателе можно разложить в степенной ряд.

Выполнять разложение сложных функций и произведения функций удобно по следующей схеме. А) Задаемся показателем степени n , до которого мы будем проводить разложение.
Б) Применяем приведенные ниже формулы разложения функций в ряд Тейлора, сохраняя в них члены до включительно, и отбрасывая члены с при , или заменяя их на .
В) В сложных функциях делаем замены переменных так, чтобы аргумент каждой ее части стремился к нулю при . Например,
.
Здесь при . Тогда можно использовать разложение функции в окрестности точки .

Примечание. Разложение функции в ряд Тейлора, в окрестности точки , называется рядом Маклорена. Поэтому для применяемых в наших целях рядов уместны оба названия.

Видео:Дифференциальное уравнение ведет к разложению в ряд Тейлора и сумме ряда?Скачать

Применяемые свойства о малого

Определение и доказательство свойств о малого приводится на странице: «О большое и о малое. Сравнение функций». Здесь мы приводим свойства, используемые при решении пределов разложением в ряд Маклорена (то есть при ).

Далее m и n – натуральные числа, .
;
;
, если ;
;
;
;
, где ;
, где c ≠ 0 – постоянная;
.

Для доказательства этих свойств нужно выразить о малое через бесконечно малую функцию:
, где .

Видео:Разложения e^x и sin(x) в ряды Тейлора.Скачать

Разложение элементарных функций в ряд Тейлора (Маклорена)

Далее приводятся разложения элементарных функций в степенной ряд при . Как мы упоминали ранее, ряд Тейлора в окрестности точки называется рядом Маклорена.

Видео:10. Ряд Тейлора. Ряд МаклоренаСкачать

Примеры

Все примеры Далее мы приводим подробные решения следующих пределов с помощью ряда Тейлора.
⇓, ⇓, ⇓, ⇓, ⇓.

Пример 1

Все примеры ⇑ Вычислить предел последовательности, используя разложение в ряд Тейлора.
.

Это неопределенность вида бесконечность минус бесконечность. Приводим ее к неопределенности вида 0/0 . Для этого выполняем преобразования.

.
Здесь мы учли, что номер элемента последовательности n может принимать только положительные значения. Поэтому . Делаем замену переменной . При . Будем искать предел считая, что x – действительное число. Если предел существует, то он существует и для любой последовательности , сходящейся к нулю. В том числе и для последовательности .

.
Раскладываем функцию в числителе в ряд Тейлора. Применяем формулу:
.
Оставляем только линейный член.
.
.
Здесь мы учли, что поскольку существует двусторонний предел , то существуют равные ему односторонние пределы. Поэтому .

Пример 2

Все примеры ⇑ Показать, что значение второго замечательного предела можно получить, используя разложение в ряд Тейлора.

Делаем замену переменной . Тогда . При . Подставляем.
.

Для вычисления предела можно считать, что значения переменной t принадлежат любой, наперед выбранной, проколотой окрестности точки . Мы полагаем, что . Используем то, что экспонента и натуральный логарифм являются обратными функциями по отношению друг к другу. Тогда
.

Вычисляем предел в показателе, используя следующее разложение в ряд Тейлора:
.
.

Поскольку экспонента является непрерывной функцией для всех значений аргумента, то по теореме о пределе непрерывной функции от функции имеем:
.

Пример 3

Все примеры ⇑ Вычислить предел, используя разложение в ряд Тейлора.
.

Это неопределенность вида 0/0 . Используем следующие разложения функций в окрестности точки :
;
;
.

Раскладываем с точностью до квадратичных членов:
;
.
Делим числитель и знаменатель на и находим предел:
.

Пример 4

Все примеры ⇑ Решить предел с помощью ряда Тейлора.
.

Легко видеть, что это неопределенность вида 0/0 . Раскрываем ее, применяя разложения функций в ряд Тейлора. Используем приведенное выше разложение для гиперболического синуса ⇑:
(П4.1) .
В разложении экспоненты, заменим x на –x :
(П4.2) .
Далее, – сложная функция. Сделаем замену переменной . При . Поэтому мы можем используем разложение натурального логарифма в окрестности точки . Используем приведенное выше разложение, в котором переименуем переменную x в t :
(П4.3) .

Заметим, что если бы у нас была функция , то при . Поэтому подставить в предыдущее разложение нельзя, поскольку оно применимо в окрестности точки . В этом случае нам потребовалось бы выполнить следующее преобразование:
.
Тогда при и мы могли бы применить разложение (П4.3).

Попробуем решить предел, выполняя разложение до первой степени переменной x : . То есть оставляем только постоянные члены, не зависящие от x : , и линейные . Остальные будем отбрасывать. Точнее переносить в .
;
;
.
Поскольку , то в разложении логарифма мы отбрасываем члены, начиная со степени 2. Применяя, приведенные выше свойства о малого имеем:

.
Подставляем в предел:

.
Мы снова получили неопределенность вида 0/0 . Значит разложения до степени не достаточно.

Если мы выполним разложение до степени , то опять получим неопределенность:
.

Выполним разложение до степени . То есть будем оставлять только постоянные члены и члены с множителями . Остальные включаем в .
;
;

;

.
Далее замечаем, что . Поэтому в разложении логарифма нужно отбросить члены, начиная со степени , включив их в . Используем разложение (П4.3), заменив t на :

Подставляем в исходную функцию.

.
Находим предел.
.

Пример 5

Все примеры ⇑ Найти предел с помощью ряда Тейлора.
.

Будем проводить разложение числителя и знаменателя в ряд Маклорена до четвертой степени включительно.

Теперь переходим к числителю. При . Поэтому сделать подстановку и применить разложение для нельзя, поскольку это разложение применимо при , а у нас . Заметим, что . Поэтому выполним преобразование.
.
Теперь можно сделать подстановку , поскольку при .

Разложим функцию и ее степени в ряд Тейлора в окрестности точки . Применяем приведенное выше разложение ⇑.
;
;

;
;
;
;
Далее заметим, что . Поэтому, чтобы получить разложение сложной функции с точностью до , нам нужно разложить с точностью до .

Разложим второй логарифм. Приводим его к виду , где при .
,
где .

Разложим z в ряд Тейлора в окрестности точки с точностью до .
Применим разложение синуса ⇑:
.
Заменим x на :
. Тогда
;

;
Заметим, что . Поэтому, чтобы получить разложение сложной функции с точностью до , нам нужно разложить с точностью до .

Раскладываем с точностью до и учитываем, что .

;
.

Подставляем разложение числителя и знаменателя и находим предел.
;
.

Использованная литература:
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.

Автор: Олег Одинцов . Опубликовано: 29-04-2019

Видео:Математический анализ, 39 урок, Формулы и ряды Тейлора и МаклоренаСкачать

Ряд Тейлора

Видео:Новогодний предел через ряд ТейлораСкачать

Понятие ряда Тейлора.

Если функция (f(x)) определена в некоторой окрестности точки (x_) и имеет в точке (x_) производные всех порядков, то степенной ряд
$$
f(x_) + sum_^frac<f^(x_)>(x-x_)^label
$$
называется рядом Тейлора функции (f) в точке (x_).

Пусть функция (f) регулярна в точке (x_), то есть представляется в некоторой окрестности точки (x_) сходящимся к этой функции степенным рядом
$$
f(x) = sum_^a_(x-x_)^,quad |x-x_| 0.label
$$
Тогда по теореме, доказанной здесь, функция (f) бесконечно дифференцируема в окрестности точки (x_), причем коэффициенты ряда eqref выражаются формулами
$$
a_ = f(x_),quad a_ = frac<f^(x_)>,quad n in mathbb.label
$$
Таким образом, степенной ряд для функции (f(x)), регулярной в данной точке (a), совпадает с рядом Тейлора функции (f) в точке (a).

Если известно, что функция (f(x)) бесконечно дифференцируема в точке (a) (и даже в некоторой окрестности этой точки), то нельзя утверждать, что составленный для этой функции ряд Тейлора eqref сходится при (x neq x_) к функции (f(x)).

Рассмотрим функцию (f(x) = e^<-1/x^>), (x neq 0), (f(0) = 0). Эта функция определена на (R),
$$
f'(x) = frac<x^>e^<-1/x^>, f″(x) = left(frac<x^>-frac<x^>right)e^<-1/x^>quadmbox x neq 0,nonumber
$$
откуда с помощью индукции легко показать, что
$$
f^(x) = e^<-1/x^> Q_ left(fracright) mbox x neq 0,nonumber
$$
где (Q_(t)) — многочлен степени (3n) от (t). Воспользуемся тем, что (displaystylelim_frac<|x|^>e^<-1/x^>=0) для любого (k in mathbb) (решение можно посмотреть здесь), и докажем, что
$$
f^(0) = 0 mbox k in mathbb.label
$$
Утверждение eqref верно при (k = 1), так как (f'(0) = displaystylelim_frac<e^<-1/x^>> = 0), откуда, предположив, что формула eqref справедлива при (k = n), находим
$$
f^(0) = lim_frac<f^(x)-f^(0)> = lim_ frac Q_ left(fracright) e^<-1/x^> = 0.nonumber
$$
Таким образом, по индукции доказано равенство eqref, и поэтому все коэффициенты ряда Тейлора eqref в точке (x_ = 0) для рассматриваемой функции равны нулю.

Так как (e^<-1/x^> neq 0) при (x neq 0), то сумма ряда Тейлора для функции (f) не совпадает с (f(x)) при (x neq 0). Иначе говоря, эту функцию нельзя представить рядом Тейлора, сходящимся к ней в окрестности точки (x_ = 0).

Причина этого явления становится понятной, если функцию (f) рассматривать в комплексной плоскости. В самом деле, функция (f(z) = e^<-1/z^>) не является непрерывной в точке (z = 0), так как (f(x) = e^<-1/x^> rightarrow 0) при (x rightarrow 0), a (f(iy) = e^<1/y^> rightarrow +infty) при (y rightarrow 0).

Видео:Частное решение ДУ, с помощью рядаСкачать

Остаточный член формулы Тейлора.

Пусть функция (f(x)) бесконечно дифференцируема в точке (x_). Тогда ей можно поставить в соответствие ряд eqref. Обозначим
$$
S_(x) = sum_^frac<f^(x_)>(x-x_)^,label
$$
$$
r_(x) = f(x)-S_(x)label
$$
и назовем (r_(x)) остаточным членом формулы Тейлора для функции (f) в точке (x_). Если существует
$$
lim_ r_(x) = 0,label
$$
то согласно определению сходимости ряда ряд eqref сходится к функции (f(x)) в точке (x), то есть
$$
f(x) = sum_^frac<f^(x_)>(x-x_)^.label
$$

Если функции (f(x)), (f'(x)), …, (f^(x)) непрерывны на интервале (Delta = (x_-delta, x_ + delta)), где (delta > 0), то для любого (x in Delta) остаточный член формулы Тейлора для функции (f) в точке (x_) можно представить:

(circ) Формула eqref доказана в здесь. Докажем формулу eqref методом индукции. В силу равенств eqref и eqref нужно показать, что
$$
f(x)-f(x_) = sum_^frac<f^(x_)>(x-x_)^ + frac intlimits_<x_>^ (x-t)^f^(t) dt.label
$$

Воспользуемся равенством (displaystyleintlimits_<x_>^ f'(t) dt = f(x)-f(x_)) и преобразуем его левую часть с помощью формулы интегрирования по частям:
$$
intlimits_<x_>^ f'(t) dt =-left.intlimits_<x_>^ f'(t)d(x-t) = [-f'(x)(x-t)]right|_<t = x_>^ + intlimits_<x_>^ (x-t)f″(t) dt =\= f'(x_)(x-x_) + intlimits_<x_>^ (x-t)f″(t) dt.nonumber
$$
Таким образом,
$$
f(x)-f(x_) = f'(x_)(x-x_) + intlimits_<x_>^ (x-t)f″(t) dt,nonumber
$$
то есть формула eqref верна при (n = 1). Предположим, что формула eqref является верной для номера (n-1), то есть
$$
f(x)-f(x_) = sum_^frac<f^(x_)>(x-x_)^ + frac intlimits_<x_>^ (x-t)^f^(t) dt.label
$$
Преобразуем интеграл в правой части формулы eqref, применив формулу интегрирования по частям:
$$
frac intlimits_<x_>^ (x-t)^f^(t) dt = -frac intlimits_<x_>^ f^(t)dt((x-t)^) =\= left.left(-fracf^(t)(x-t)^right)right|_<t = x_>^ + frac intlimits_<x_>^(x-t)^f^(t) dt =\= fracf^(x_)(x-x_)^ + frac intlimits_<x_>^(x-t)^f^(t) dt.nonumber
$$
Отсюда следует, что равенство eqref можно записать в виде eqref. Формула eqref доказана. (bullet)

Если функция (f) и все ее производные ограничены в совокупности на интервале (Delta = (x_-delta, x_ + delta)), то есть
$$
exists M > 0: forall x in Delta rightarrow |f^(x)| leq M, n = 0,1,2,ldots,label
$$
то функция (f) представляется сходящимся к ней в каждой точке интервала (Delta) рядом Тейлора eqref.

(circ) Пусть (x in (x_-delta, x_ + delta)). Тогда, используя формулу eqref и условие eqref, получаем
$$
|r_(x)| leq M frac<|x-x_|^>.label
$$

Так как (displaystylelim_ frac<a^> = 0) для любого (a > 0) (пример разобран здесь), то из eqref следует, что выполняется условие eqref, то есть в точке (x) справедливо равенство eqref. (bullet)

Теорема 2 остается в силе, если условие eqref заменить следующим условием:
$$
exists M > 0 exists C > 0: forall x in Delta rightarrow |f^(x)| leq MC^, n = 0, 1, 2, ldotsnonumber
$$

Видео:[Calculus | глава 11] Ряд ТейлораСкачать

Разложение элементарных функций в ряд Тейлора.

Найдем разложение основных элементарных функций в ряд Тейлора в окрестности точки (x_ = 0), то есть в ряд вида
$$
f(x) = sum_^frac<f^(0)>x^,label
$$
который называют рядом Маклорена. Заметим, что коэффициенты (displaystylefrac<f^(0)>) разложения eqref для основных элементарных функций (показательной, гиперболических, тригонометрических и других) были найдены в разделе про формулу Тейлора.

Разложение показательной и гиперболической функций в ряд Тейлора.

Пусть (f(x) = e^). Тогда для любого (x in (-rho, rho)), где (rho > 0), выполняются неравенства
$$
0 0), то есть радиус сходимости этого ряда (R = +infty). Так как для функции (f(x) = e^) выполняются равенства (f(0) = 1), (f^(0) = 1) для любого (n), то по формуле eqref получаем разложение в ряд Маклорена показательной функции
$$
e^ = sum_^frac<x^>,label
$$

Используя разложение eqref и формулы
$$
operatorname x = frac <e^+ e^>,quad operatorname x = frac<e^-e^>,nonumber
$$
находим разложения в ряд Маклорена гиперболического косинуса и гиперболического синуса:
$$
operatorname x = sum_^frac<x^>,label
$$
$$
operatorname x = sum_^frac<x^>,label
$$
Радиус сходимости каждого из рядов eqref, eqref (R = +infty).

Разложение тригонометрических функций в ряд Тейлора.

Пусть (f(x) = sin x). Тогда (|f(x)| leq 1) и (|f^(x)| leq 1) для всех (n in mathbb) и для всех (x in R). По теореме 2 ряд eqrefдля функции (f(x) = sin x) сходится для любого (x in (-infty, +infty)), то есть радиус сходимости этого ряда (R = +infty).

Если (f(x) = sin x), то (f(0) = 0), (f^(0) = 0), (f'(0) = 1), (f^(0) = (-1)^) для любого (n), и по формулеeqrefполучаем разложение синуса в ряд Маклорена:
$$
sin x = sum_<substack>^ frac<(-1)^>x^.label
$$

Пусть (f(x) = cos x). Тогда (|f(x)| leq 1), (|f^(x)| leq 1) для всех (n) и для всех (x in R), (f(0) = 1), (f'(0) = 0), (f^(0) = (-1)^) и, (f^(0) = 0) для всех (n). По формуле eqref получаем
$$
cos x = sum_^ frac<(-1)^>x^.label
$$
Радиус сходимости каждого из рядов eqref и eqref (R = +infty).

Разложение логарифмической функции в ряд Тейлора.

(circ) Оценим остаточный член (r_(x)), пользуясь формулой eqref при (x_ = 0). Преобразуем эту формулу, полагая (t = tau x). Тогда (dt = x dtau), (1-x =x(1-tau)) и формула eqref примет вид
$$
r_(x) = frac<x^> intlimits_0^1 (1-tau) f^(tau x) dtau.label
$$

Если (f(x) = ln(x + 1)), то по формуле eqref, используя равенство eqref, получаем
$$
r_(x) = (-1)^x^ intlimits_0^1 frac<(1-tau)^><(1 + tau x)^> d tau.label
$$

Пусть (|x| 1), то (displaystylelim_ frac<n^><(1/|x|)^> = 0). Поэтому из соотношения eqref следует, что (r_(x) rightarrow 0) при (n rightarrow infty) для каждого (x in (-1, 1)), то есть справедливо равенство eqref, причем радиус сходимости ряда eqref в случае, когда (alpha neq 0) и (alpha notin mathbb), равен 1. (bullet)

В заключение заметим, что при разложении функций в ряд Тейлора обычно используют формулы eqref—eqref, eqref-eqref и применяют такие приемы, как: представление данной функции в виде линейной комбинации функций, ряды Тейлора для которых известны; замена переменного; почленное дифференцирование и интегрирование ряда.

Разложить в ряд Маклорена функцию (f(x)) и найти радиус сходимости (R) ряда, если:

(triangle) Используя формулу eqref, получаем ряд
$$
frac<1 + x^> = sum_^ (-1)^x^,label
$$
радиус сходимости которого (R = 1).
Из равенства eqref следует, что (displaystylefrac<sqrt<1 + x^>> = sum_^ C_^x^), где
$$
C_^ = frac<displaystyleleft(-fracright)left(-frac-1right)ldotsleft(-frac-(n-1)right)>= frac<(-1)^1cdot3ldots(2n-1)><2^n!> = frac<(-1)^(2n-1)!!><2^n!>.nonumber
$$
Следовательно,
$$
frac<sqrt<1 + x^>> = 1 + sum_^ frac<(-1)^(2n-1)!!><2^n!>x^, R = 1.label
$$
Так как (f(x) = displaystylefrac+ frac= frac<displaystyle2left(1 + fracright)>-frac<displaystyle3left(1-fracright)>), то, применяя формулы eqref и eqref, получаем ряд
$$
frac<x^-x-6> = sum_^ left(frac<(-1)^><2^>-frac<3^>right)x^, R = 2. blacktrianglenonumber
$$

Разложить в ряд Маклорена функции
$$
operatorname x,nonumber
$$
$$
operatorname x,nonumber
$$
$$
ln(x + sqrt<1 + x^>),nonumber
$$
и найти радиусы сходимости (R) рядов.

(triangle) Почленно интегрируя ряд eqref, получаем
$$
operatorname x = intlimits_0^x frac
<1 + t^> = sum_^ (-1)^ frac<x^>,quad R = 1.nonumber
$$
Заменяя в формуле eqref (x^) на (-x^), получаем
$$
frac<sqrt<1-x^>> = 1 + sum_^ frac<2^n!>x^,quad R = 1.nonumber
$$
откуда следует, что
$$
operatorname x = intlimits_0^x frac
<1-t^> = x + sum_^ frac<2^n!(2n + 1)>x^, R = 1.nonumber
$$
Почленно интегрируя ряд eqref, получаем
$$
ln(x + sqrt<1 + x^>) = intlimits_0^x frac
<1 + t^> = x + sum_^ frac<(-1)^(2n-1)!!><2^n!(2n + 1)>x^, R = 1. blacktrianglenonumber
$$

Разложить в ряд Тейлора в точке (x_ = 2) функцию (f(x) = ln(4 + 3x-x^)).

(triangle) Так как (4 + 3x-x^ = -(x-4)(x + 1)), то, полагая (t = x-2), получаем
$$
f(x) = ln(4-x)(x + 1) = g(t) = ln(2-t)(3 + t) = ln 6 + lnleft(1-fracright) + lnleft(1 + fracright).nonumber
$$
Используя формулы eqref и eqref, отсюда находим
$$
g(t) = ln 6-sum_^ frac<t^><n2^> + sum_^ frac<(-1)^t^><n3^>,quad |t|

Видео:Формула ТейлораСкачать

Элементарные функции комплексного переменного.

Используя равенства eqref и формулы eqref, eqref, находим
$$
frac <e^+ e^> = cos z, frac<e^-e^> = sin z,label
$$
откуда следует, что
$$
e^ = cos z + i sin z.label
$$
Полагая в формуле eqref (z = z_) и (z = z_). и перемножая соответствующие ряды, можно показать, что
$$
e^<z_>e^<z_> = e^ <z_+ z_>.label
$$

Пусть (z = x + iy), где (x in R), (y in R). Тогда из равенства eqref и формулы eqref находим
$$
e^ = e^ = e^(cos y + i sin y).label
$$
Из формулы eqref следует, что
$$
e^ = e^,nonumber
$$
то есть (e^) — периодическая функция с периодом (2pi i). Поэтому для каждого комплексного (z neq 0) уравнение
$$
e^ = zlabel
$$
имеет бесконечное множество решений вида (w + i2pi n), где (w) — одно из решений уравнения eqref, (n in Z).

Если (w = u + iv), то (z = e^ = e^(cos v + i sin v)), откуда получаем
$$
|z| = e^,quad u = ln |z|,quad v = arg z.nonumber
$$

Пусть (varphi) — какое-нибудь значение аргумента числа (z). Тогда
$$
v = varphi + 2pi n, n in Z.nonumber
$$
Таким образом, все решения уравнения eqref, если их обозначить символом (operatorname z), задаются формулой
$$
operatorname z = ln |z| + i(varphi + 2pi n),label
$$
где (varphi) — одно из значений аргумента числа (z) ((z neq 0)), (n in Z).

По заданному значению (z) значение (w) из уравнения eqref определяется, согласно формуле eqref, неоднозначно (говорят, что логарифмическая функция (operatorname z) является многозначной).

Разложить в степенной ряд в окрестности точки (z = 0) функцию (f(z) = e^sin z).

(triangle) Используя формулы eqref и eqref, получаем
$$
f(z) = e^left(frac<e^-e^>right) = frac(e^-e^).nonumber
$$
Так как (1 + i = sqrte^), (1-i = sqrte^), то по формуле eqref находим
$$
f(z) = sum_^ frac<2^> left(frac<e^-e^>right)z^,nonumber
$$
откуда в силу второго из равенств eqref следует, что
$$
e^sin z = sum_^ frac<2^> sin fracz^.nonumber
$$
Радиус сходимости ряда (R = +infty). (blacktriangle)