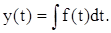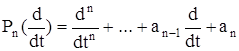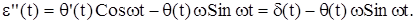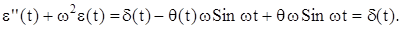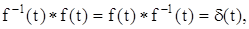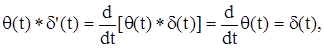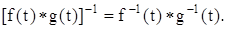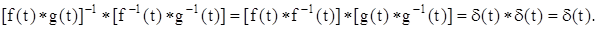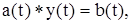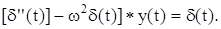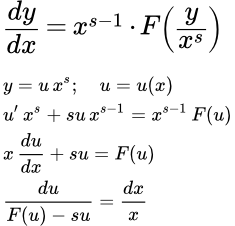Решение уравнения в обобщенных функциях

Если f(t) – обычная функция, то его решением является первообразная, то есть

Пусть теперь f(t) – обобщенная функция.

Определение. Обобщенная функция g(t) называется первообразной обобщенной функцией f(t), если

Если f(t) – сингулярная обобщенная функция, то возможны случаи, когда ее первообразная – регулярная обобщенная функция. Например, первообразная d(t) является y(t) = q(t); первообразная q(t) является функция y(t) = t₊, а решение уравнения

можно записать в виде

Рассмотрим линейное уравнение n-го порядка с постоянными коэффициентами

(4)

где f(t) – обобщенная функция. Обозначим

дифференциальный полином n-го порядка.

Определение. Обобщенным решением дифференциального уравнения (4) называется обобщенная функция y(t), для которой выполняется соотношение

Если f(t) – непрерывная функция, тогда единственным решением уравнения (4.) является классическое решение.

Определение. Фундаментальным решением уравнения (4) называется любая обобщенная функция e(t) такая, что

Функция Грина – фундаментальное решение, удовлетворяющее данному граничному, начальному или асимптотическому условию.

Теорема. Решение уравнения (4) существует и имеет вид

(5)

если только свертка определена.

По свойству свертки имеем

В качестве примера рассмотрим уравнение

(6)

Нетрудно видеть, что фундаментальным решением этого уравнения является

6. Пространство обобщенных функций

Совокупность обобщенных функций, порождаемых основным пространством K, образует пространство K’. Рассмотрим подпространство обобщенных функций пространства K, состоящее их обобщенных функций, равных нулю вне некоторого конечного интервала принадлежащего [0, ¥]. Введем в этом пространстве операцию умножения двух функций в виде свертки этих функций. Если f(t), g(t) Î то и Кроме того свертка обладает всеми свойствами обычной операции умножения. Роль единицы в играет функция d(t), так как для

Пусть существует такая что

тогда f -1 (t) называется обратной обобщенной функцией f(t).

Пространство 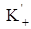с введенной операцией умножения образует алгебру (коммутативную) со сверткой.

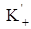
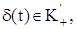
Рассмотрим алгебру со сверткой . Обобщенная функция так как она равна нулю всюду, кроме точки ноль. Обобщенная функция сосредоточена вначале координат, поэтому Далее,

Теорема. Пусть для существуют обратные функции f — 1 (t) и g -1 (t). Тогда свертка имеет обратную функцию вида

Рассмотрим следующее определенное в уравнение в свертках

Свертка существует для любой обобщенной функции так как

Следовательно, y(t) является фундаментальным решением уравнения (4). В частности, фундаментальное решение уравнения (6) с оператором 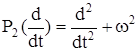принадлежит алгебре со сверткой Следовательно,

Рассмотрим операционный метод решения уравнения в свертках. Пусть имеется уравнение

где a(t) и b(t) Î Среди эффективных методов решения этого уравнения приведем метод преобразования Лапласа. Применив преобразование Лапласа к левой и правой части этого уравнения, имеем

Если для функции L(p) существует оригинал, принадлежащий 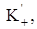то он и является искомым решением.

В качестве примера рассмотрим уравнение

Применив к нему преобразование Лапласа, получим (р 2 -w 2 ) L[y(t)] = 1.

Видео:Уравнения математической физики. Дельта-функция Дирака. Обобщенные функции.Скачать

Обобщенные однородные дифференциальные уравнения первого порядка

Видео:Лекция 5. Обобщенные функции. Часть 2Скачать

Определение

Видео:Дифференциирование обобщённых функцийСкачать

Как определить, является ли дифференциальное уравнение обобщенным однородным

Для того, чтобы определить, является ли дифференциальное уравнение обобщенным однородным, нужно ввести постоянную t и сделать замену:
y → t α · y , x → t·x .
Если удастся выбрать такое значение α , при котором постоянная t сократится, то это – обобщенное однородное дифференциальное уравнение. Изменение производной y′ при такой замене имеет вид:
.

Пример

Определить, является ли данное уравнение обобщенным однородным:
.

Делаем замену y → t α · y , x → t·x , y′ → t α– 1 y′ :
;
.
Разделим на t α+ 5 :
;
.
Уравнение не будет содержать t , если
4 α – 6 = 0 , α = 3/2 .
Поскольку при α = 3/2 , t сократилось, то это обобщенное однородное уравнение.

Видео:Теория обобщённых функцийСкачать

Метод решения

Рассмотрим обобщенное однородное дифференциальное уравнение первого порядка:
(1) .
Покажем, что оно приводится к однородному уравнению с помощью подстановки:
t = x α .
Действительно,
.
Отсюда
; .
Подставляем в исходное уравнение (1):
;
.

Это – однородное уравнение. Оно решается подстановкой:
y = z · t ,
где z – функция от t .
При решении задач, проще сразу применять подстановку:
y = z x α ,
где z – функция от x .

Видео:Шапошникова Т. А. - Уравнения с частными производными - Обобщенные решения волнового уравненияСкачать

Пример решения обобщенного однородного дифференциального уравнения первого порядка

Решить дифференциальное уравнение
(П.1) .

Проверим, является ли данное уравнение обобщенным однородным. Для этого в (П.1) делаем замену:
y → t α · y , x → t·x , y′ → t α– 1 y′ .
.
Разделим на t α :
.
t сократится, если положить α = – 1 . Значит – это обобщенное однородное уравнение.

Делаем подстановку:
y = z x α = z x – 1 ,
где z – функция от x .
.
Подставляем в исходное уравнение (П.1):
(П.1) ;
;
.
Умножим на x и раскрываем скобки:
;
;
.
Разделяем переменные – умножим на dx и разделим на x z 2 . При z ≠ 0 имеем:
.
Интегрируем, пользуясь таблицей интегралов:
;
;
;
.
Потенцируем:
.
Заменим постоянную e C → C и уберем знак модуля, поскольку выбор нужного знака определяется выбором знака постоянной С :
.

Возвращаемся к переменной y . Подставляем z = xy :
.
Делим на x :
(П.2) .

Когда мы делили на z 2 , мы предполагали, что z ≠ 0 . Теперь рассмотрим решение z = xy = 0 , или y = 0 .
Поскольку при y = 0 , левая часть выражения (П.2) не определена, то к полученному общему интегралу, добавим решение y = 0 .

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 03-08-2012 Изменено: 24-06-2015

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Решение обыкновенных дифференциальных уравнений операторным методом в обобщенных функциях Текст научной статьи по специальности « Математика»

Видео:Математика | Решение уравненийСкачать

Похожие темы научных работ по математике , автор научной работы — В. П. Тимощенко

Видео:Тихонов Н. А. - Методы математической физики - Функция ГринаСкачать

Текст научной работы на тему «Решение обыкновенных дифференциальных уравнений операторным методом в обобщенных функциях»

ТОМСКОГО ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ ПОЛИТЕХНИЧЕСКОГО

ИНСТИТУТА имени С. М. КИРОВА

РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ОПЕРАТОРНЫМ МЕТОДОМ В ОБОБЩЕННЫХ

(Представлена научным семинаром вычислительной лаборатории ТПИ)

В работах [3, 4] строилось операторное исчисление на основе понятия обобщенной функции и разрабатывался аппарат для решения дифференциальных уравнений с постоянными коэффициентами. В настоящей работе операторный метод в обобщенных функциях распространяется на обыкновенные дифференциальные уравнения, имеющие как переменные, так и постоянные коэффициенты.

I. Множество К всех вещественных функций ф(х), каждая из которых имеет непрерывные производные всех порядков и финитна, т. е. обращается в нуль вне некоторой конечной области (зависящей от ф)г называется осноеным пространством основных финитных функций.

Последовательность основных функций ср, (х), • • ■ > ?п(х)> • ■ *

называется сходящейся к нулю в пространстве К, если эти функции обращаются в нуль вне одной и той же ограниченной области и равномерно сходятся к нулю так же, как и их производные любого порядка.

Каждый линейный непрерывный функционал, определенный на основном пространстве К, называется обобщенной функцией (см. [1], стр. 13).

Функционал, который ставит в соответствие каждой функции ф(х) ее значение в точке Хо^О, будем называть дельта-функцией и обозначать через 6(х); таким образом,

где ‘s (x) — произвольная основная функция из К; a¿ — const; pi = 0,1; ii = 0,1; gi(x) — бесконечно дифференцируемые функции; i — О, 1,2, . , л — 1.

Заметим, что для оператора Г (5, х) операции дифференцирования и умножения на функцию не перестановочны.

Сверткой /, ■■■■ fo двух обобщенных функций /х и /■> называется обобщенная функция, определяемая на любой’ основной функции ? равенством

(/. — и 0 (1) при следующих начальных данных Коши:

у(*>(0) = 0, к = 0, 1,2. п-2

Такое задание начальных условий не нарушает общности задачи Копш для уравнения (1), так как всякое уравнение порядка п, удовлетворяющее произвольным начальным данным

УФ) ‘ — Уо , К : — 0, I, 2, . , п— I,

можно с помощью некоторого преобразования свести к новому уравнению, удовлетворяющему начальным условиям (2).

Коэффициенты gi (х), . , gn-i(x) будем полагать беско-

нечно дифференцируемыми функциями, и при том некоторые из них могут быть постоянными величинами, а правую часть f(x) — непрерывной функцией на всей оси [0, сю). Решение же уравнения (I) будем искать на множестве К+ .

В операторной форме уравнение (I), с учетом условий (2), запишется следующим образом:

Если существует единственная обобщенная функция yf:K+ , удовлетворяющая уравнению (I) и условиям (2), то у будем называть решением этого уравнения и обозначать

0(,у) — I 0(,9)—I о (.у) — 1

Производя формально деление функции /, а затем ¿-функции на оператор ¿>»5) — Т (я, х), мы получим решение в виде следующего ряда:

🔍 Видео

Горицкий А. Ю. - Уравнения математической физики. Часть 2. Семинары - Семинар 5Скачать

Попов И.Ю. Обобщенные функции. Часть 2Скачать

Палин В.В. - Уравнения математической физики - 3.Операции над обобщенными функциямиСкачать

10. Уравнения БернуллиСкачать

Горицкий А. Ю. - Уравнения математической физики - Обобщённое энтропийное решениеСкачать

Лекция №6 по УМФ. Обобщённое дифференцирование и его корректность. Константинов Р.В.Скачать

Горицкий А. Ю. - Уравнения математической физики - Обобщённые решенияСкачать

Шапошникова Т.А. - Уравнения с частными производными. Часть 2. Семинары - Семинар 3Скачать

Шейпак И.А. - Функциональный анализ. Часть 2. Лекции - 5. Решение простейших уравненийСкачать

Гармонический анализ 13. Пространство Шварца и обобщенные функции.Скачать

Консультация №11. Мат. анализ. Обобщенные функции. Решение разных задачСкачать