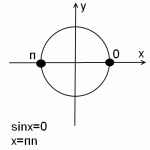Решение уравнения удовлетворяющее условию sinx 0 или sinx 0

Разделы: Математика

Раскрытие модуля по определению

Модулем числа а называется само это число а, если а ≥ 0, и число -а, если а 2 x-sinx=0

sinx=0 или sinx= (оба уравнения удовлетворяют условию sinx≥0)

Решаем уравнение второй системы, и выбирая те, которые удовлетворяют условию sinx 2

cosx=0 или x+1,5=1 или x-1,5 = -1

х= -0,5 х = -2,5

Условию cosx≥0 не удовлетворяет х = -2,5 (3 четверть)

Ответ:

№5. Найти все решения уравнения на отрезке [0;4].

Решение. Перепишем уравнение в виде

Раскрывая знак модуля, получаем системы:

Решая первую систему, получим

Из серии в нужном промежутке [0;4] лежат точки 0 и ; , а из серии

Решая вторую систему, получим систему , которая не имеет решений.

Ответ:

№6 Решить уравнение.

Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и левая часть, тогда 2х-4≥0, 2(х-2)≥0 , х-2≥0. Если х-2≥0. то при раскрытия правого модуля по определению рассматривается только один случай:

х=2

Выберем те корни, которые удовлетворяют условию: х-2≥0; х≥2

№7. Решить уравнение.

Решение. ОДЗ:

Раскрывая знак модуля, получаем системы:

Решая первую систему, получим cos2x=0, и из решений надо выбрать те, при которых sinx>0. На круге видно, что это точки вида

Решая вторую систему, получим уравнение соs2x=2,не имеющее решений.

Ответ:

№8. Решить уравнение.

Решение. Преобразуем уравнение следующим образом:

Ответ:

№9. Решить уравнение.

Решение. Выражение под первым модулем всегда неотрицательно, и его можно сразу отбросить. Второй модуль раскрываем по определению.

Решить уравнение первой система аналитически невозможно, исследуем поведение левой и правой частей на данных промежутках. Функция f(x) =-x 2 +15x-45=(-x 2 +15x-44)-1≤-1

при причем, f(х)= -1 в точках 4 и 11.Левая часть cos при любых х, причем, в точках 4 и 11 не равна -1, значит, система решений не имеет.

При решении уравнения второй системы получается:

В промежутке только одно целое нечетное число 3, т.е

Другие способы раскрытия модулей.

Уравнения вида можно решать и следующим способом:

№10. Решить уравнение.

Решение. Левая часть уравнения неотрицательна, значит, неотрицательна и правая часть, тогда cosx 21.02.2008

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

Калькулятор онлайн.
Решение тригонометрических уравнений.

Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите тригонометрическое уравнение
Решить уравнение

Видео:10 класс. Решение уравнений sin x = aСкачать

Немного теории.

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Тригонометрические уравнения

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Уравнение cos(х) = а

Из определения косинуса следует, что ( -1 leqslant cos alpha leqslant 1 ). Поэтому если |a| > 1, то уравнение cos x = a не имеет корней. Например, уравнение cos х = -1,5 не имеет корней.

Уравнение cos x = а, где ( |a| leqslant 1 ), имеет на отрезке ( 0 leqslant x leqslant pi ) только один корень. Если ( a geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac right] ); если a

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Уравнение sin(х) = а

Из определения синуса следует, что ( -1 leqslant sin alpha leqslant 1 ). Поэтому если |a| > 1, то уравнение sin x = а не имеет корней. Например, уравнение sin x = 2 не имеет корней.

Уравнение sin х = а, где ( |a| leqslant 1 ), на отрезке ( left[ -frac; ; frac right] ) имеет только один корень. Если ( a geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac right] ); если а

Видео:Частное решение дифференциального уравнения. 11 класс.Скачать

Уравнение tg(х) = а

Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.

Уравнение tg x = а для любого a имеет на интервале ( left( -frac; ; frac right) ) только один корень. Если ( |a| geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac right) ); если а

Видео:Решите уравнение ★ cos⁡x+sin⁡x=1 ★ Как решать простые уравнения?Скачать

Решение тригонометрических уравнений

Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.

Видео:Уравнения вида f(sinx±cosx; sinxcosx) = 0. Н.А. ЛебедеваСкачать

Уравнения, сводящиеся к квадратным

Решить уравнение 2 cos 2 (х) — 5 sin(х) + 1 = 0

Заменяя cos 2 (х) на 1 — sin 2 (х), получаем
2 (1 — sin 2 (х)) — 5 sin(х) + 1 = 0, или
2 sin 2 (х) + 5 sin(х) — 3 = 0.
Обозначая sin(х) = у, получаем 2у 2 + 5y — 3 = 0, откуда y₁ = -3, y₂ = 0,5
1) sin(х) = — 3 — уравнение не имеет корней, так как |-3| > 1;
2) sin(х) = 0,5; ( x = (-1)^n text(0,5) + pi n = (-1)^n frac + pi n, ; n in mathbb )
Ответ ( x = (-1)^n frac + pi n, ; n in mathbb )

Решить уравнение 2 cos 2 (6х) + 8 sin(3х) cos(3x) — 4 = 0

Используя формулы
sin 2 (6x) + cos 2 (6x) = 1, sin(6х) = 2 sin(3x) cos(3x)
преобразуем уравнение:
3 (1 — sin 2 (6х)) + 4 sin(6х) — 4 = 0 => 3 sin 2 (6х) — 4 sin(6x) + 1 = 0
Обозначим sin 6x = y, получим уравнение
3y 2 — 4y +1 =0, откуда y₁ = 1, y₂ = 1/3

Видео:Задача. Решите тригонометрическое уравнение: ∜12⋅sinx + √cosx = 0Скачать

Уравнение вида a sin(x) + b cos(x) = c

Решить уравнение 2 sin(x) + cos(x) — 2 = 0

Используя формулы ( sin(x) = 2sinfrac cosfrac, ; cos(x) = cos^2 frac -sin^2 frac ) и записывая правую часть уравпения в виде ( 2 = 2 cdot 1 = 2 left( sin^2 frac + cos^2 frac right) ) получаем

Поделив это уравнение на ( cos^2 frac ) получим равносильное уравнение ( 3 text^2frac — 4 textfrac +1 = 0 )
Обозначая ( textfrac = y ) получаем уравнение 3y 2 — 4y + 1 = 0, откуда y₁=1, y₁= 1/3

В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях ( a neq 0, ; b neq 0, ; c neq 0, ; c^2 leqslant b^2+c^2 ) можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на ( sqrt ):

Решить уравнение 4 sin(x) + 3 cos(x) = 5

Здесь a = 4, b = 3, ( sqrt = 5 ). Поделим обе части уравнения на 5:

Видео:Решение однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать

Уравнения, решаемые разложением левой части на множители

Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.

Решить уравнение sin(2х) — sin(x) = 0
Используя формулу синуса двойного аргумента, запишем уравнепие в виде 2 sin(x) cos(x) — sin(x) = 0. Вынося общий множитель sin(x) за скобки, получаем sin(x) (2 cos x — 1) = 0

Решить уравнение cos(3х) cos(x) = cos(2x)
cos(2х) = cos (3х — х) = cos(3х) cos(x) + sin(3х) sin(x), поэтому уравнение примет вид sin(x) sin(3х) = 0

Решить уравнение 6 sin 2 (x) + 2 sin 2 (2x) = 5
Выразим sin 2 (x) через cos(2x)
Так как cos(2x) = cos 2 (x) — sin 2 (x), то
cos(2x) = 1 — sin 2 (x) — sin 2 (x), cos(2x) = 1 — 2 sin 2 (x), откуда
sin 2 (x) = 1/2 (1 — cos(2x))
Поэтому исходное уравнение можно записать так:
3(1 — cos(2x)) + 2 (1 — cos 2 (2х)) = 5
2 cos 2 (2х) + 3 cos(2х) = 0
cos(2х) (2 cos(2x) + 3) = 0

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

sinx=0

Эта ассоциация позволяет легко запомнить, где синус равен 0, и быстро решить уравнение sin x=0.

Как обычно, частные случаи синуса рассматриваем на единичной окружности.

Используем ассоциацию косинус-колобок. Оба начинаются с ко-, в названии cos x буква o тоже косвенно на колобка указывает. Колобок движется по горизонтали. На координатной плоскости движение по горизонтали происходит вдоль оси x.

Поэтому cos x — это x, соответственно, sin x — это y.

Таким образом, чтобы найти, где синус равен 0, нужно выяснить, в каких точках y=0.

Раз y=0, то движения вверх-вниз не происходит.

На единичной окружности условию sin x=0 удовлетворяют две точки: 0 и π.

Чтобы из одной точки попасть в другую, надо пройти половину окружности, то есть π.

Поскольку таких точек, в которых синус равен 0, бесконечное множество, прибавляем не π, а πn, где n — целое число (то есть n принадлежит Z): x=0+πn.

Следовательно, решение уравнения sin x=0, есть множество точек

🎥 Видео

Частное решение ДУ, с помощью рядаСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Уравнение sin x = 1/2Скачать

✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive​​ #041 | Борис ТрушинСкачать

Элементарные тригонометрические уравнения: sin(x)=a и cos(x)=aСкачать

Математика это не ИсламСкачать