Решение уравнения теплопроводности в матлабе

Видео:Нестационарное уравнение теплопроводности в матлабеl Time dependent heat transfer equation in MatLabСкачать

Метод Finite Volume — реализация на примере теплопроводности

Метод Finite Volume (FVM)

В основе метода лежит разбиение области на непересекающиеся контрольные объемы(элементы), узловые точки, в которых ищется решение.Узловые точки находятся в центрах контрольных объемов.Также, как и для метода конечных разностей, для каждого элемента составляется уравнение, получается система линейных уравнений.Решая ее — находим значения
искомых переменных в узловых точках.Для отдельного элемента уравнение получается путем интегрирования исходного дифф уравнения по элементу и аппроксимации интегралов.

Термин конечный объем в статье будет часто заменятся на Элемент, будем для удобства считать их эквивалентами (элемент в данной статье не имеет ничего общего с методом конечных элементов).

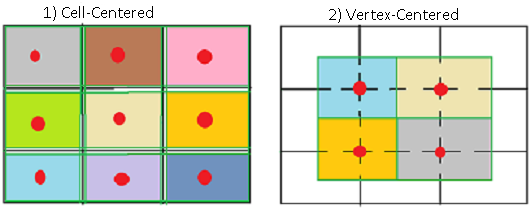
Есть 2 различных способа решения задачи по FVM:
1) грани контрольного объема совпадают с гранями элемента
2) грани контрольного объема проходят через центры граней элементов(на которые разбита область).Искомые переменные хранятся в вершинах этих элементов.Вокруг каждой вершины строится контрольный объем. Для непрямоугольной сетки этот способ имеет еще 2 подвида.

Мы будем использовать способ 1) с контрольными объемами совпадающими с элементами на которые разбита область.

Некоторые плюсы FVM:

• сохранение основных величин по всей области, таких как энергия системы, масса, тепловые потоки и тд.Причом это условие выполняется даже для грубой расчетной сетки
• высокая скорость расчета.Многие расчетные величины можно вычислить при разбиении области на элементы, и вычислять их на каждом шаге по времени нет необходимости.
• легкость использования для задач со сложной геометрией и криволинейными границами.Легкость использования разных геометрических типов элементов — треугольники, полигоны.

Метод FVM реализуем на примере уравнения теплопроводности:

Итак основные шаги при реализации FVM:

1. Перевод дифф уравнения в форму пригодную для FVM — интегрирование по контрольному объему
2. Составление дискретного аналога, выбор способа перевода производных и других подынтегральных выражений в дискретную форму
3. Получение уравнения для каждого из контрольных объемов, на которые разбита область.Составление системы линейных уравнений и ее решение.

Дискретизация по времени.

Немного теории или первый шаг в реализации FVM

FVM на стандартной прямоугольной сетке

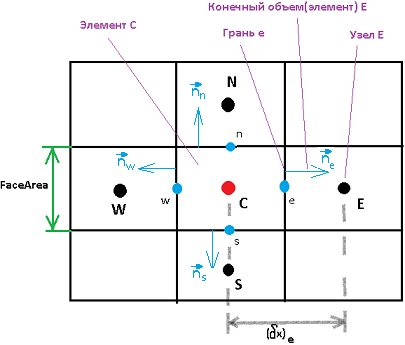
На рисунке изображен Элемент С и его соседние элементы справа(E), слева(W), сверху(N) и снизу(S).У элемента С есть 4 грани обозначенные буквами e w n s.Именно эти 4 грани и составляют периметр элемента и по ним производится интегрирование.Для каждого элемента в результате получаем дискретный аналог исходного дифф уравнения.

Составим дискретный аналог для элемента С.Для начала нужно разобраться с интегралом (3).Интеграл это ведь по факту сумма.Поэтому мы и заменяем интеграл по всей поверхности элемента, на сумму по 4-м составляющим этой поверхности, тоесть 4 граням элемента.

Уравнение (7) и есть конечное уравнение для элемента С, из него мы на каждом шаге по времени получаем новое значение температуры (Tnew) в элементе С.

Граничные условия на прямоугольной сетке

Мы рассмотрим только 2 вида граничных условий.

1. Задана температура Tb на границе
2. Задан поток FluxB на границе, рассмотрим только случай когда FluxB=0, т.е. грань e будет теплоизолирована(Insulated)

Случай 2) самый простой, поскольку получается что грань e не потребуется при дискретизации(т.к. все коэффициенты Flux=0) и можно ее просто пропустить.

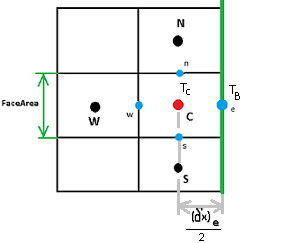
Теперь рассмотрим случай 1).Дискретизация грани e будет в целом похожа на ту что уже была описана.Будут только 2 изменения — вместо Te будет известное граничное значение Tb и вместо расстояния DXe будет DXe/2.В остальном можно рассматривать значение Te так, как будто это был бы обычный соседний узел E.Теперь подробнее распишем терм для граничного элемента С.

Пример численных расчетов на прямоугольной сетке

FVM в задачах со сложной геометрией

Здесь как раз проявляется преимущество FVM, где также, как и в методе конечных элементов, можно представлять область с круглыми границами через разбиение на треугольники или любые другие полигоны.Но FVM имеет еще 1 плюс — при переходе от треугольников к полигонам с большим числом сторон не требуется абсолютно ничего менять, конечно если код был написан для произвольного треугольника а не равностороннего.Более того, можно без изменения кода использовать смесь разных элементов — треугольники, полигоны, квадраты и тд.

Рассмотрим общий случай, когда вектор соединяющий центры 2-х элементов не совпадает с вектором нормали к общей грани этих элементов.Вычисление потока flux через грань теперь будет состоять из 2-х частей.В первой будет расcчитываться ортогональная составляющая а во второй так называемая «кросс-диффузия».

На картинке изображены 2 элемента, С — текущий рассматриваемый элемент и F — соседний элемент.Опишем дискретизацию для грани, разделяющей эти 2 элемента.Вектор соединяющий центры элементов — DCF.Вектор e — это единичный вектор по направлению DCF.Вектор Sf — направлен по нормали к грани, его длинна равна длине грани.

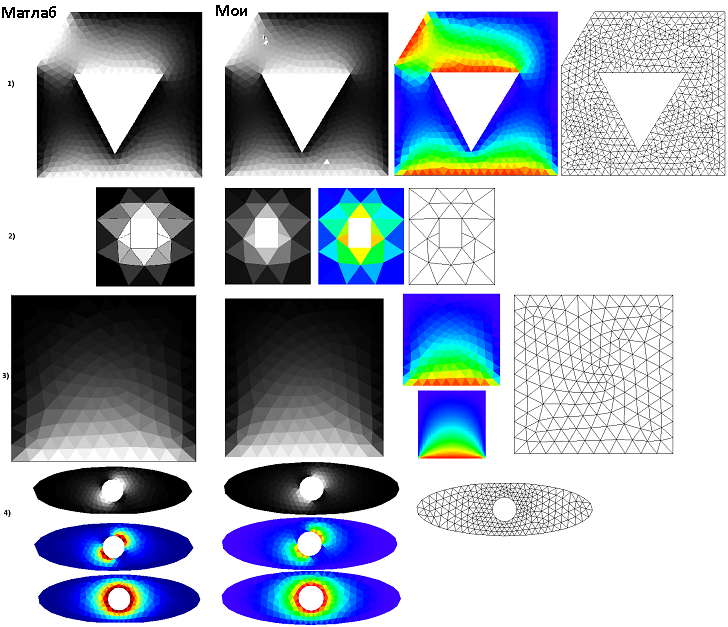
В исходниках я не стал реализовывать терм с кроссдиффузией, т.к встал вопрос — как проверить корректность такой реализации.Визуально сравнение результатов Матлаб и моих ничем не отличалось в отсутствии кросс-диффузии.Видимо это связано с тем что Матлаб любит треугольники близкие к равносторонним, что в итоге делает кроссдиффузию=0.Возможно позже еще вернусь к этому вопросу.

Расчет граничных элементов ничем не отличается от расчетов не на границе, вместо центра соседнего элемента берется центр грани, ну и как обычно подставляется температура на границе.
В моей реализации в итоге получается так:

Примеры и проверка результатов

Описание структуры исходников

Гитхаб с исходниками лежит тут
Основная версия в папке heat2PolyV2.То что относится к вычислительной части лежит в heat2PolyV2SrcFiniteVolume.

Вначале файла Scene2.cs — параметры которые можно менять для отображения в разных цветовых схемах, масштаб, отображение mesh и т.д.Сами примеры хранятся в heat2PolyV2binDebugDemos
Выгрузку из Матлаба сделать просто — нужно открыть pde toolbox, открыть m файл (либо создать самому с нуля), зайти в меню Mesh-Экспорт mesh, нажать ОК; перейти в основной Матлаб, в панельке появятся переменные — матрицы p e t, открыть файл savemymesh.m, выполнить его, появится файл p.out, перенести его в папку Demos.
В исходниках для выбора примера необходимо задать имя файла в строке param.file = «p»;(FormParam.cs).Далее необходимо применить граничные условия — для готовых примеров можно просто раскомментировать соответствующие блоки в MainSolver.cs:

Смысл тут простой — Матлаб разделяет границы по доменам, например внешние и внутренние.Также для каждого домена границы разбиты на части (группы), чтобы можно было задавать условия на участках границы по отдельности — например справа или снизу.
Возможно и вовсе не использовать Матлаб, а вручную прописать все элементы(треугольники) и их вершины + грани(только для граничных элементов)

Видео:Двумерное нестационарное уравнение теплопроводности в MatLab l 2D Heat transfer equation in MatLabСкачать

Нахождение решения уравнения теплопроводности с помощью языка программирования MatLab Текст научной статьи по специальности « Математика»

Видео:Решение уравнения теплопроводности методом конечных разностейСкачать

Аннотация научной статьи по математике, автор научной работы — Булгаков Александр Иванович, Малютина Елена Валерьевна, Филиппова Ольга Викторовна

В работе находится численное решение уравнения теплопроводности. Рассматривается пример стабильной явной численной схемы.

Видео:Уравнение теплопроводности в цилиндрических координатахСкачать

Похожие темы научных работ по математике , автор научной работы — Булгаков Александр Иванович, Малютина Елена Валерьевна, Филиппова Ольга Викторовна

Видео:Трёхмерное уравнение теплопроводности с ф.п. l 3D Heat transfer equation with phase change in matlabСкачать

SOLVING THE HEAT EQUATION WITH MATLAB

We study to obtain the numerical solution of heat equation by means of MatLab. We consider example of stable explicit scheme for a heat equation.

Видео:Численное решение уравнения теплопроводностиСкачать

Текст научной работы на тему «Нахождение решения уравнения теплопроводности с помощью языка программирования MatLab»

10. Самойленко А. М., Перестюк Н. А. Дифференциальные уравнения с импульсными воздействиями. К.: Вища шк., 1987.

Поступила в редакцию 10 ноября 2011 г.

БЛАГОДАРНОСТИ: Работа выполнена при финансовой поддержке Российского Фонда Фундаментальных Исследований (проекты № 11-01-00645, № 11-01-00626), ФЦП «Научные и научно-педагогические кадры инновационной России на 2009-2013 годы», Министерства образования и науки РФ (проект № 1.1877.2011), гранта NATO NRCLR.9837 16.

Bulgakov A.I., Grigorenko A.A., Panasenko E.A. Inclusions with Volterra in the sense of A.N. Tikhonov operators and impulsive perturbations. For Volterra inclusions with impulsive perturbations there are considered the problems of local solvability and extendability of solutions. It is proved that the right end-point of the interval on which all the solutions exist depends lower semi-continuously on the parameters. It is also shown that, if the inclusion is a-priori bounded for some parameter, then this parameter value can not be an isolated point, in the sense of a-priori boundedness, moreover the solutions set is Hausdorff upper semicontinuous at this point.

Key words: inclusions with impulse operator; extendability of solutions.

SOLVING THE HEAT EQUATION WITH MATLAB © A. I. Bulgakov, E. V. Malyutina, О. V. Filippova

Key words: numerical solution; explicit scheme.

We study to obtain the numerical solution of heat equation by means of MathLab. We consider example of stable explicit scheme for a heat equation.

We consider the following initial-boundary value problem for the heat equation:

ut = a2uxx + f (x,t) forx e (0,L),t e (0, to), (1)

u(0, t) = 0, u(L, t) = 0. (3)

We want to construct the optimal program for numerical solution of the heat equation. We will do it by means MatLab. The basic idea is to replace the derivatives involved in (l)-(3) by finite differences. We assume that (N + 1) is the number of the segmentation points in the x-direction; h = L/N is the step of grid (x-direction); Xi = ih, i = 0, 1, . N; tj = jd, where j > 0, d is the time step.

Furthermore, the grid function v , with vij= v (xi, tj ), approximates u .

Using the following approximation, we can write the initial-boundary value problem in the follows form [1—5]:

Vij+1 = -^2 (vi-i,j + Vi+ij) + П — 2^2 I Vi j + dfi j Jor i = 1. N — 1,j > 1, (4)

Vi,0 = ^i, for i = 0, 1,

Vo,j = 0, VN,j = 0, for j > 0.

For the finite difference scheme (4) we will consider possible solutions of the form

Therefore, from (4) we obtain

A — 1 2 e-iZ — 2 + eiZ

Using the equality

e-iZ — 2 + eiZ = 2 cos( — 2 = -Asin2 Z

where r = ad ■ The explicit scheme is stable if

guarantees that scheme (4) is stable. If r = ^ 2 that the scheme is stable.

We can find a numerical solution by using the MatLab’s code. WTe could enter the meanings

for N, K, a, f (x,t), p(x) and use the following code [6j:

g = (a * a * d)/(h * h) while g > 0.5

disp(’the scheme is not stable’)

g = (a * a * d)/(h * h) end

x = 0 : h : L; u(-.,1) = ^(x(:)); t = 0 : d : T; for j = 2 : K + 1 u(1,j) = 0; u(N + 1, j) = 0; end

j=1:K for k = 2 : N

u(k,j + 1) = g * (u(k — 1, j) + u(k + 1, j)) + (1 — 2 * g) * u(k,j) + d * f (x,t);

Example. We consider the initial-boundary value problem for the heat equation:

ut = uxx + sin (3^x) for x £ (0,1), t £ (0, to), (6)

u(0, t) = 0, u(1, t) = 0. (8)

We can construct the graph of the exact solution (fig. 1) and the graph of the numerical

solution (fig. 2) in MatLab:

In this example we have the number of Courant r = ^2 = 0.0125 Надоели баннеры? Вы всегда можете отключить рекламу.

Видео:Решение уравнения теплопроводности в одномерной постановке в Excel с применением неявной схемыСкачать

Лабораторная работа 4.3.Моделирование объектов с распределенными параметрами в среде системы Matlab

Модуль 4.Модели с распределенными параметрами.

Цель работы: Ознакомиться с набором инструментов PDE Toolbox на примере решения задачи распространения тепла в плоской пластине.

Краткие сведения из теории: Дифференциальное уравнение теплопроводности для одной пространственной координаты будет иметь вид

, (1)

где – частная производная температуры по времени; – частная производная второго порядка температуры по координате; – коэффициент температуропроводности; – тепловой поток внутренних источников тепла [Вт/мІ]; – плотность [кг/мі]; – теплоемкость [Дж/кг·град].

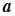
В терминах векторного анализа уравнение (1) будет иметь вид

(2а)

(2б)

(2с)

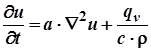
в этих уравнениях – оператор Лапласа; – оператор Гамильтона; – дивергенция градиента температуры;

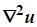
Градиент температуры – это вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры и численной равный производной от температуры по этому направлению.

Коэффициент температуропроводности характеризует скорость изменения температуры. Коэффициент температуропроводности является мерой теплоинерционных свойств тела. Из уравнения (1) следует, что изменение температуры во времени для любой точки пространства пропорционально величине . Скорость изменения температуры в любой точке тела будет тем больше, чем больше коэффициент температуропроводности. Поэтому при прочих равных условиях выравнивание температур во всех точках пространства будет происходить быстрее в том теле, которое обладает большим коэффициентом температуропроводности. Величина коэффициента температуропроводности зависит от природы вещества. Коэффициент температуропроводности можно вычислить по формуле

,[мІ/с] (3)

– коэффициент теплопроводности [Вт/м·град].

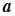
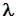
Подставляя выражение (3) уравнение (1) получим

(4)

Коэффициент теплопроводности характеризует способность тел проводить тепло. Чем больше коэффициент, тем быстрее прогревается тело.

Различают стационарный и нестационарный процессы типы передачи. При установившемся (стационарном режиме) температура тела не зависит от времени и поэтому левая часть дифференциального уравнения теплопроводности равна нулю. При нестационарном режиме температура тела зависит от времени. В случае стационарного режима используется для решения эллиптическое уравнение, а в случае нестационарного режима используется параболическое уравнение. В случае, если в теле нет внутренних источников тепла, выражение .

Для численного решения задачи распространения тепла в пластине необходимо задать начальные условия и граничные (краевые) условия.

Начальные условия устанавливают распределение температуры в теле в определенный момент времени, чаще всего в момент времени .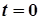

Краевые условия характеризуют тепловые условия на поверхности тела, которые должны быть известны в любой момент времени.

Различают следующие виды граничных (краевых) условий.

· Граничные условия первого рода. При этом задается распределение температуры на поверхности тела для каждого момента времени. По другому их называют еще условиями Дирихле.

· Граничные условия второго рода. При этом задаются величины теплового потока для каждой точки поверхности тела и любого момента времени. По другому их называют еще условиями Неймана. Тепловой поток пропорционален .

· Граничные условия третьего рода. При этом задается температура окружающей среды и закон теплообмена между поверхностью и окружающей средой. Граничное условие третьего рода характеризует закон теплообмена между поверхностью и окружающей средой в процессе охлаждения и нагревания тела.

· Граничные условия четвертого рода характеризуют условия теплообмена системы тел или тела с окружающей средой по закону теплопроводности.

Решение уравнений теплопроводности в пакете Matlab: В пакете Matlab дифференциальные уравнения в частных производных (PDE) могут быть решены двумя способами:

1. Путем составления программы на языке пакета Matlab;

2. При помощи специальной панели инструментов – графического интерфейса пользователя (GUI) PDE Toolbox.

В данной работе будет рассматриваться второй способ. Он позволяет решать поставленные задачи с граничными условиями Дирихле и Неймана.

Для запуска PDE Toolbox в командной строке окна управления нужно выполнить команду pdetool. После чего откроется окно, в котором находятся инструменты и рабочая область, в которой строится и отображается численное решение уравнений.

Пример: Решить задачу нагрева пластины толщиной 2 см., высотой 1,6 см. По средине пластины имеется отверстие шириной 0,1 см. и высотой 0,8 см. Продолжительность нагрева 5 секунд. Граничные условия:

· u = 100 – на левой границе;

· u = -10 – на правой границе;

· на остальных границах .

Начальное условие u(0) = 20. Вывести распределение температуре по длине пластинки.

Решение:

1.Необходимо нарисовать объект в среде PDE Toolbox. Для более точного построения необходимо перейти в режим сетки. Для этого необходимо зайти в меню Options и активизировать пункты Grid (включает и отключает режим сетки) и Snap (привязка к уздам сетки). Пункт Axes limits устанавливает границы координатных осей, а Axes Equal выравнивает масштабы осей. Для построения щели необходимо зайти в подменю Grid spacing и нанести вспомогательные линии сетки. Для изменения координатной сетки необходимо отключить режим Auto.

Рис. 1. Задание параметров осей в PDE Toolbox

2. После этого производится построение двух областей, как показано на рис. 2. В строке формул исправляется R1 + R2 на R1 — R2.

Рис. 2. Вид пластины

3. В PDE Toolbox можно задавать граничные условия Дирихле и Неймана. Зададим сначала граничные условия Неймана, которые задаются следующим образом:

· Нажимается кнопка после того, когда границы пластины будут отображаться в виде стрелок черного цвета необходимо нажать комбинацию клавиш Ctrl+A для выделения всего периметра. Равенство нулю потока есть частный случай условий Неймана. Необходимо зайти меню Boundary и выбрать пункт Specify boundary conditions. В открывшемся диалоговом окне указать тип – условия Неймана. Для получения теплоизолированных верхних и нижних границ и таких же границ пластины с отверстием необходимо, чтобы коэффициенты g (тепловой поток) и q (коэффициент теплоотдачи) были равны нулю. После этого стрелки по периметру изменят цвет на синий.

📽️ Видео

Уравнение теплопроводности с фазовым переходом в Матлабе l Solve 3D Heat transfer equation in matlabСкачать

Решение уравнения теплопроводности в одномерной постановке в ExcelСкачать

MatLab. Решение дифференциального уравнения.Скачать

Уравнение в частных производных Уравнение теплопроводностиСкачать

Задаем тепловой поток на границах двумерной пластины в MatLab l Heat flow at 2D-plate in MatLabСкачать

Решение произвольных уравнений. Методы вычислений в MATLAB. Часть 1. Урок 61Скачать

Решение нестационарного уравнения теплопроводности в двухмерной постановке в ExcelСкачать

Решение неоднородного уравнения теплопроводностиСкачать

MatLab. 7.5. Эллиптическое уравнениеСкачать

Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Решение первой краевой задачи для неоднородного уравнения теплопроводности.Скачать

6-1. Уравнение теплопроводностиСкачать