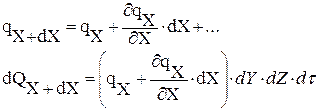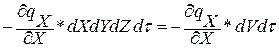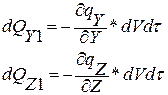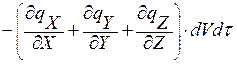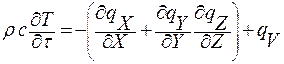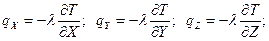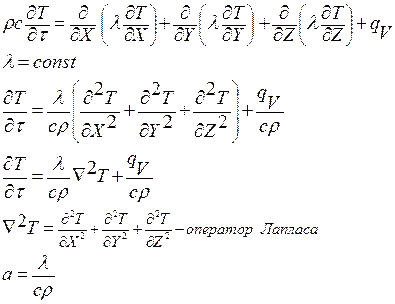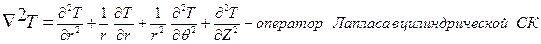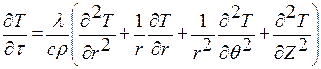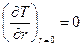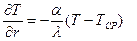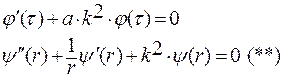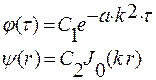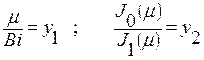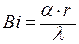Решение уравнения теплопроводности для цилиндра

Видео:6-1. Уравнение теплопроводностиСкачать

Постановка задачи и вывод дифференциального уравнения теплопроводности для сплошного цилиндра. Аналитическое решение.

Дифференциальное уравнение теплопроводности выводится на основе закона сохранения энергии. Из всего рассматриваемого объема выделим элементарный объем dV и процесс будем рассматривать в течении элементарного промежутка времени.

· Тепло физические параметры среды постоянны

· Температурной деформацией пренебрегаем

· Внутренний источник тепла , если он есть, распределен по всему объему

dQ₁ – количество тепла подведенного к рассматриваемому объему dV за время dτ за счет процессов электропроводности

dQ₂ – количество тепловой энергии, которой выделяется на dV за dτ за счет действия внутреннего источника тепла

dQ – изменение внутренней энергии рассматриваемого объема за dτ (изменение энтальпии тела).

Ø Методы переноса тепла: теплопроводность, тепловая конвекция, излучение

Ø Конвективный обмен – возможен только в подвижных средах. Перенос осуществляется только за счет перемещение самого вещества.

Ø Тепловое излучение – перенос тепла происходит в 2 этапа. Сначала тепло преобразуется в тепловую энергию, а затем обратно.

Ø Теплопроводность – перенос тепла в твердых телах, жидкостях или газах, если жидкость и газы неподвижны.

Механизм данного явления объясняется на основании молекулярно — кинетических изменений. Перенос энергии осуществляется вследствие теплового движения и энергетического взаимодействия между микрочастицами (молекулами, атомами, электронами), из которых состоит данное тело.

Теплопроводность в чистом виде существует только в твердых телах. А в подвижных средах теплообмен осуществляется за счет теплопроводности, конвекции и излучения.

По теплопроводности тепло распространяется от нагретых участков к холодным, то есть в сторону убывания температуры.

Температура определяет степень нагретости тела.

Процесс теплопроводности неразрывно связан с распределением температуры внутри тела, поэтому необходимо дать определение температурному полю и градиенту температуры:

— температурным полем называется совокупность значений температуры в каждой точке пространства в данный момент времени

Геометрическое место точек в пространстве имеющих одинаковую температуру, называется изотермической поверхностью

Поскольку любая точка пространства в данный момент времени может иметь только одно значение температуры, то изотермические поверхности не пересекаются →

— температурный градиент – предел отношения изменения температуры ΔТ к расстоянию между изотермами по нормали Δn.

Lim (ΔТ / Δn) _Δn→0 = = grad T. -единичный вектор

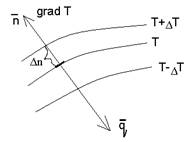
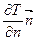
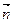
Является вектором, направленным по нормали к изотермической поверхности в сторону возрастания температуры его размерность [ 0 С/м]

Наибольшее изменение температуры может происходить по нормали к изотермическим поверхностям.

· Количества тепла, прошедшего через произвольную изотермическую поверхность за некоторый интервал времени τ – будем обозначать P [Вт]

· Количества тепла, прошедшего через произвольный изотермическую поверхность в единицу времени будем обозначать – тепловой поток Q [Дж].

· Тепловой поток отнесенный к единице поверхности, называется плотностью теплового потока – q [Вт/м 2 ]

· Закон Фурье (связь q и grad T). Фурье экспериментально установил что, количество переданного тепла пропорционально падению температуры, времени и площади сечения, перпендикулярного направлению распространению тепла

· λ – коэффициент теплопроводности – представляет собой количество тепла, которое роходит в единицу времени через один квадратный метр изотремической поверхности при температурном градиенте =1

, [Вт/м 0 С]

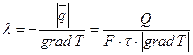
В общем случаи λ зависит от температуры

· С – теплоемкость – количество энергии необходимого для нагрева 1 кг вещества на 1 градус. [Дж/кг 0 С]

dQ_X = q_X * dY * dZ * dτ

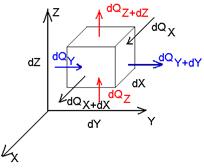
dQ_X1 = dQ_X — dQ_X+dX =

dQ₁ = dQ_X1 + dQ_Y1 + dQ_Z1 =

dQ₂ = q_V dV dτ, где q_V – количества тепла выделившегося в единице объема в единицу времени (внутренний источник тепла).

dQ = dU = ρ C 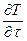dV dτ , где ρ – плотность среды [кг/м 3 ]

Из закона Фурье:

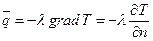
а – коэффициент температура проводность [м 2 / 0 С]

Постановка задачи:

1. рассматриваем сплошной цилиндр

2. процесс изотермический

3. цилиндрическая система координат

4. теплофизические свойства постоянны

5. внутреннего источника тепла нет (q_V =0)

Переходим от декартовой системы координат к цилиндрической:

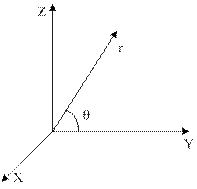	Цилиндрические (Ц) и декартовые (Д) координаты связаны следующим образом:
Д ® Ц	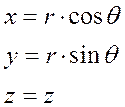Ц ® Д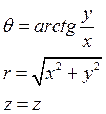

Оператор Лапласа для цилиндрической системы координат запишется:

С учетом поставленной задачи получаем:

Охлаждение (нагревание) бесконечного длинного цилиндра.

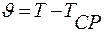
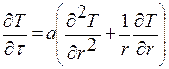
Цилиндр радиусом г₀ отдает теплоту окружающей среде через свою боковую поверхность; коэффициент теплоотдачи α во всех точках поверхности одинаков и остается постоянным на протяжении всего периода охлаждения. Температура среды Tcp постоянна. В начальный момент времени при τ = 0 температура является некоторой функцией T (r, 0) = f (r). При этих условиях уравнение теплопроводности принимает вид:

(*)

Граничные и начальные условия:

· при τ = 0 и 0 0 и r = 0

· при τ > 0 и r = r₀

Сформулированную задачу решим с помощью разделения переменных, т. е.

(r, τ) = φ (τ) ψ (r).

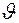
Подставив это выражение в уравнение (*),получим два обыкновенных дифференциальных уравнения вида

Если обозначить kr₀ = μ , тогда частное решение уравнения (*) будет иметь вид:

(1)

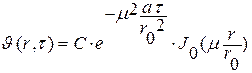
где 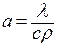— коэффициент температуро-проводность

Постоянная μ определяется из граничных условий (r= r₀), решение которых приводит к характеристическому уравнению:

(2) где J₁, (μ) — функция Бесселя первого рода первого порядка.

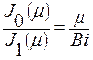
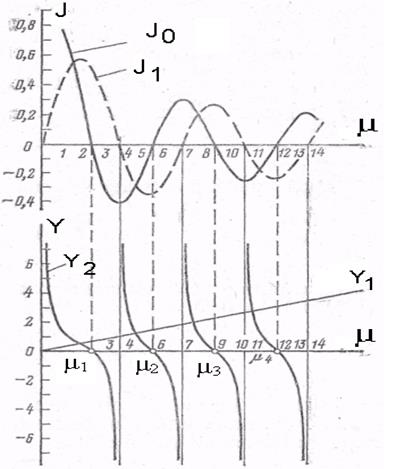
Уравнение (+) является трансцендентным, и его удобно решать графическим способом, обозначив:

· Отметим, что у₂ обращается в нуль в тех точках, для которых Jo (μ) = 0.

· В тех точках, в которых функция J₁ (μ₁) обращается в нуль, функция у₂ претерпевает разрыв непрерывности и становится равной ± оо.

Функ­ции Jo (μ) и J₁ (μ) являются периодическими затухающими функциями.

— Кривая у₂ = напоминает котангенсоиду, но с убывающим периодом.

— Функция у₁ графически представляет прямую линию, проходящую через начало координат.

Выполнив построение, как показано на рис, в точках пересечения функции у₂ с прямой у₁ получим значения корней характеристического уравнения

Из рис следует, что уравнение (2) имеет бесчисленное множество решений, а сами корни, представляют ряд возрастающих чисел, т. е. μ₁ 100) прямая совпадает с осью абсцисс и корни характеристического уравнения не зависят от Bi, а определяются из условий

· Если рассматривать охлаждение цилиндра при условии Bi → 0

(практически Bi 2 = 2Bi.

· Если Fo ≥ 0,25, при вычислении безразмерной температуры можно ограничиться первым членом ряда. Допускаемая при этом ошибка не превысит 1 %.

Дата добавления: 2016-04-19 ; просмотров: 2824 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Уравнение теплопроводности в цилиндрических координатахСкачать

Об одной задаче теплопроводности для цилиндра с конвективным теплообменом Текст научной статьи по специальности « Физика»

Видео:Уравнение теплопроводности в цилиндрических координатахСкачать

Аннотация научной статьи по физике, автор научной работы — Жорник Александр Иванович, Киричек Виктория Александровна, Савочка Петр Анатольевич

Рассматривается нестационарная задача теплопроводности для цилиндра с конвективным теплообменом со средой с кипящим слоем. Этот кипящий слой образуется между поверхностью цилиндра и охлаждающей жидкостью. В зависимости от плотности теплового потока, подводимого к жидкости от поверхности нагрева, на ней образуется или сплошной слой пара, или отдельные паровые пузыри, или кипение прекращается, если температура поверхности окажется ниже точки кипения. Поэтому коэффициент теплообмена является функцией температуры поверхности цилиндра , и поэтому задача имеет нелинейное граничное условие. Решение проводится численным и приближенным аналитическим методами. Полученные указанными методами результаты сравниваются.

Видео:12. Как остывает шар (решение уравнения теплопроводности)Скачать

Похожие темы научных работ по физике , автор научной работы — Жорник Александр Иванович, Киричек Виктория Александровна, Савочка Петр Анатольевич

Видео:8.1 Решение уравнения теплопроводности на отрезкеСкачать

ON A THERMAL CONDUCTIVITY PROBLEM FOR A CYLINDER WITH CONVECTIVE HEAT EXCHANGE

A nonstationary thermal conductivity problem for a cylinder with a convective heat exchange with a medium with a fluidized bed is considered. This fluidized bed is formed between the cylindrical surface and the coolant. Depending on the heat flux density supplied to the fluid from the heating surface, a continuous layer or separate vapor bubbles form on it. Otherwise boiling ceases when the surface temperature is below the boiling point. Therefore, the heat transfer coefficient is a function of cylinder temperature, therefore we have a nonlinear boundary condition. The solution is carried out by numerical and approximate analytical methods. The results obtained by these methods are compared.

Видео:Уравнение в частных производных Уравнение теплопроводностиСкачать

Текст научной работы на тему «Об одной задаче теплопроводности для цилиндра с конвективным теплообменом»

в случае 2(д-1)-а >0 и а, не ограничено (а1 : Л

коэффициент Био при температуре выше 133 °С (в нашем случае Б11 =

=107, для гс = 2,15-10-3 м, ЛТ = 0,5852 Вт/м-К, а> = 29-103 Вт/м2К ), Бг2 — коэффициент Био при температуре ниже 100 °С (в нашем случае Бг2 = 37, 55, 74 при тех же гс и ЛТ и различных коэффициентах теплообмена).

Для построения решения разностной схемы будем использовать равномерную сетку на интервале ре [0,1]:

где кр — шаг по относительному радиусу р, кт — по шаг по относительному времени т, М — количество точек разбиения по относительному радиусу, N — количество точек разбиения по относительному времени, т0 — время, для которого будет производиться расчет.

После всех преобразований получим разностную схему: 1) I = 0

1 — M + 0,5 1 — M — 0,5 —

lM гт_2 lM —1 oi2 lM —1

Известно, что данная схема абсолютно устойчива [4, 5]. Схема будет монотонной при условии

Т(г, г) = /(г), 0 0, дТ (г , г).

_ -к[Т(г,г)-в], г = гс, г > 0, дг

относительный коэффициент теплообмена.

Решение поставленной выше задачи проведено методом конечного интегрального преобразования Ханкеля по г [6] и имеет вид

где Го _ —, в = —т г Л

■, хк — корни трансцендентного уравнения

В начальный момент времени цилиндр нагрет до постоянной температуры Т0 выше температуры кипения воды (охлаждающей среды). Поэтому на начальном этапе охлаждения температура стенки выше температуры кипения. В связи с этим охлаждение будет проходить при пузырьковом кипении с коэффициентом теплообмена а1. Полагая в (9) /(г) = Т0, имеем решение в виде

где уп — корни трансцендентного уравнения

у11(у) = Вг’11о(у). (12)

Для нахождения времени Го1, при котором температура поверхности станет равной температуре кипения жидкости Тк = 100 °С, необходимо воспользоваться следующим условием:

Подставляя Го1 в (11), найдем начальное распределение температур /(г) для следующего этапа охлаждения с другим коэффициентом теплообмена Вг2:

(Уп) (Уп2 + Вг-12)1о и

Подставляя (14) в (9), найдем температурное поле на следующем этапе охлаждения:

120 (хк) (( + Вг22) 0

где хк — корни трансцендентного уравнения

Можно показать, что если В11 = Вг2 = В1ср, то решение (15) переходит в решение (11).

На рис. 3, 4 приведены графики зависимости температуры на поверхности цилиндра от времени, рассчитанные численным методом (рис. 3) и приближенным аналитическим методом (рис. 4) — пунктирные линии. Сплошными линиями показано решение, полученное по (11) при В[1 = Вг2 = В1ср = 90 (аср = 25-103 Вт/м2К).

Из рис. 3, 4 видно, что численный метод (рис. 3) дает более плавный температурный профиль, чем профиль, найденный приближенным аналитическим методом. Это связано с тем, как указывалось выше, что в приближенном аналитическом методе температурная область перехода от теплообмена с пузырьковым кипением к теплообмену с жидкостью, с температурой ниже точки кипения, заменена точкой.

Рис. 3. Сравнение температурных полей со средним коэффициентом (В1ср = 90, сплошная линия) и изменяющимся скачком (от В11 = 107 до Ы2 = 37, 55,

74, пунктирные линии)

Рис. 4. Сравнение температурных полей с средним коэффициентом (В1ср = 90, сплошная линия) и изменяющимся скачком (от В11 = 107 до В12 = 37, 55, 74,

Заключение. Решение задачи теплопроводности для цилиндра с конвективным теплообменом в среду с кипящим слоем численным и приближенным аналитическим методом показало относительно хорошее совпадение результатов расчета.

1. Кутателадзе С.С. Основы теории теплообмена. — Новосибирск: Наука, Сибирское отделение. — 1970. — 659 с.

2. Михеев М.А. Основы теплопередачи. — М.: Госэнергоиздат, 1956. — 526 с.

3. Бартенев Г.М. Механические свойства и тепловая обработка стекла. — М.: Гос. Изд-во лит-ры по строительству, архитектуре и строительным материалам, 1960. — 166 с.

4. Самарский А.А., Гулин А.В. Численные методы. — М.: Наука, 1989. — 432 с.

5. Яненко Н.Н. Метод дробных шагов решения многомерных задач математической физики. — Новосибирск: Наука, Сиб. отд-ние, 1967. — 195 с.

6. Жорник А.И. Термоупругие процессы, происходящие в твердых телах с трещиноподоб-ными дефектами. — Таганрог: Изд-во Таганрогского госпединститута, 2002. — 259 с.

Статью рекомендовал к опубликованию д.ф.-м.н., профессор Г.В. Куповых.

Жорник Александр Иванович — Таганрогский государственный педагогический институт им. А.П. Чехова; e-mail: Zhornik@land.ru; г. Таганрог, ул. Инициативная, 48; тел.: 88634601807; кафедра теоретической, общей физики и технологии, д.ф.-м.н.; профессор.

Киричек Виктория Александровна — кафедра теоретической, общей физики и технологии; к.ф.-м.н.; доцент.

Савочка Петр Анатольевич — Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Южный федеральный университет»; e-mail: Savochka07@mail.ru; 347928, г. Таганрог, пер. Некрасовский, 44; тел.: 88634360460; кафедра конструирования электронных средств; ассистент.

Zhornik Aleksandr Ivanovich — Taganrog State Pedagogical Institute named A.P. Chekhov; e-mail: Zhornik@land.ru; 48, Initsiativnaya street, Taganrog, Russia; phone: +78634601807; the department of theoretical physics and general technology; dr. of phys.-math. sc.; professor.

Kirichek Viktoriya Aleksandrovna — the department of theoretical physics and general technology; cand. of phys.-math. sc.; professor.

Видео:15. Решение уравнения теплопроводности в кругеСкачать

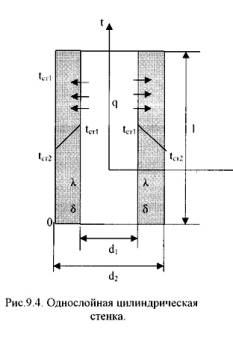
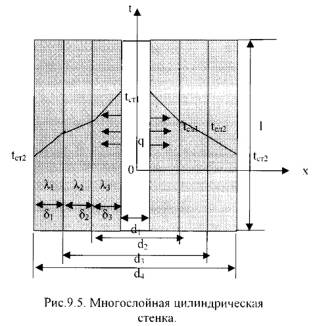
9.3. Стационарная теплопроводность через цилиндрическую стенку

1). Однородная цилиндрическая стенка.

Рассмотрим однородный однослойный цилиндр длиной l, внутренним диаметром d₁и внешним диаметром d₂ (Рис.9.4).

Уравнение теплопроводности по закону Фурье в цилиндрических координатах: Q = — λ∙2∙π∙r ·l· ∂t / ∂r (9.24)илиQ = 2·π·λ·l·Δt/ln(d₂/d₁), (9.25)где: Δt = t_ст1 – t_ст2 – температурный напор;

λ – κоэффициент теплопроводности стенки.

Для цилиндрических поверхностей вводят понятия тепловой поток единицы длины цилиндрической поверхности (линейная плотность теплового потока), для которой расчетные формулы будут:q_l = Q/l =2·π·λ·Δt /ln(d₂/d₁), [Вт/м]. (9.26)Температура тела внутри стенки с координатойd_х:t_x = t_ст1 – (t_ст1 – t_ст2) ·ln(d_x/d₁) / ln(d₂/d₁). (9.27)2). Многослойная цилиндрическая стенка.

Допустим цилиндрическая стенка состоит из трех плотно прилегающих слоев (Рис.9.5).

Температура внутренней поверхности стенки –t_ст1, температуранаружнойповерхности стенки –t_ст2, коэффициенты теплопроводности слоев -λ₁, λ₂, λ₃, диаметры слоев d₁, d₂, d₃, d₄.

🌟 Видео

Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Численное решение уравнения теплопроводностиСкачать

Решение первой краевой задачи для неоднородного уравнения теплопроводности.Скачать

Теплопроводность цилиндрической стенкиСкачать

Решение задачи Коши для уравнения теплопроводности (Часть 1)Скачать

Решение уравнения теплопроводности методом конечных разностейСкачать

Решение уравнения теплопроводности в одномерной постановке в ExcelСкачать

Метод Фурье для неоднородного уравнения теплопроводностиСкачать

Решение первой начально-краевой задачи для одномерного уравнения теплопроводности.Скачать

Интуитивное понимание формулы теплопроводности (часть 11) | Термодинамика | ФизикаСкачать

Решение задачи Коши для уравнения теплопроводности (Часть 2)Скачать

Уравнение теплопроводности на полупрямой (решение задачи)Скачать