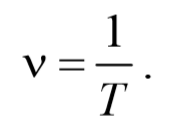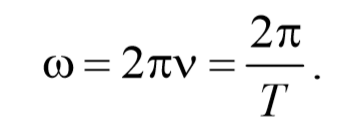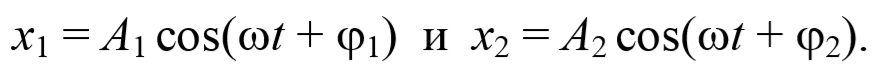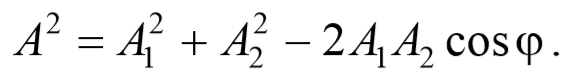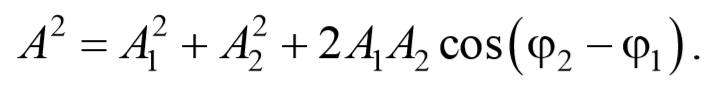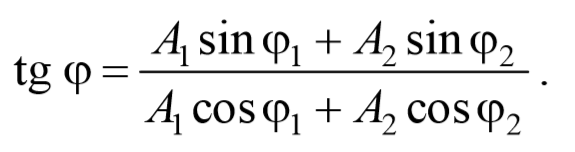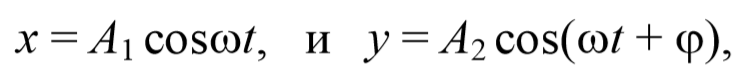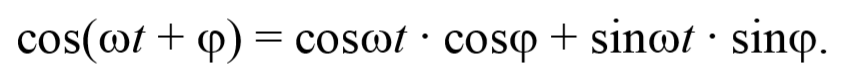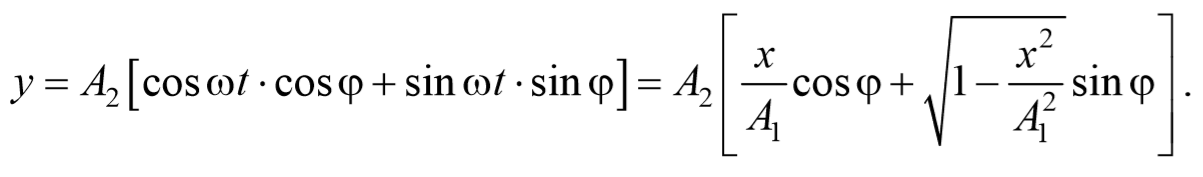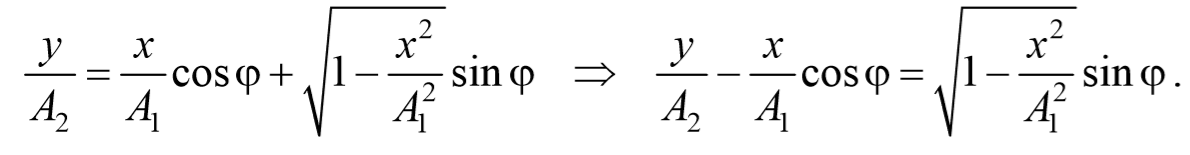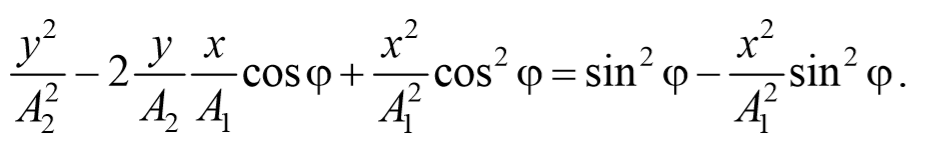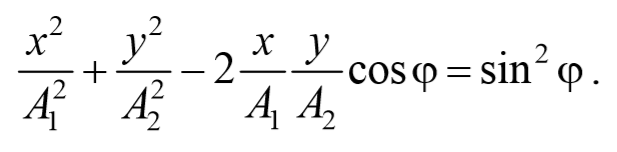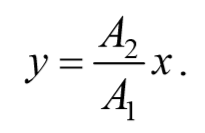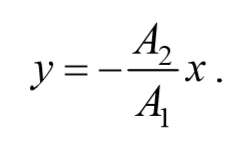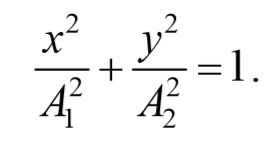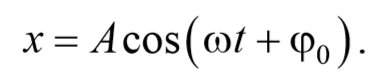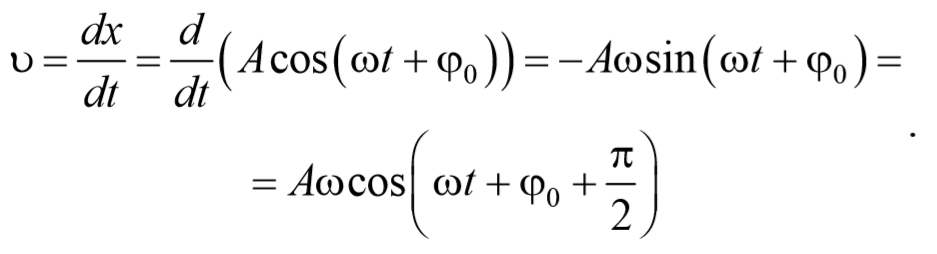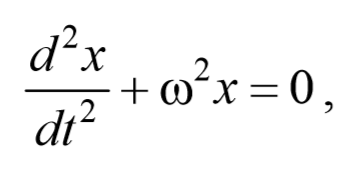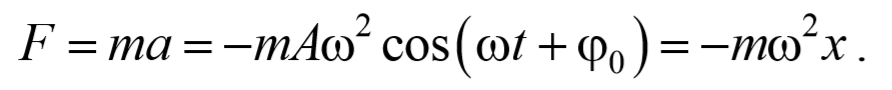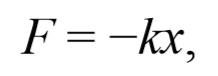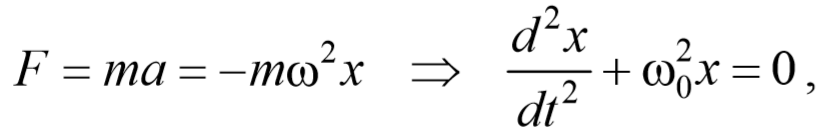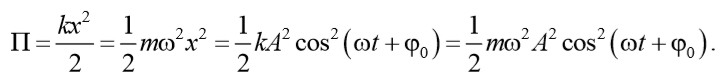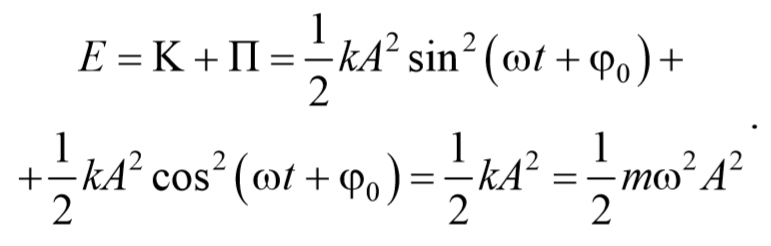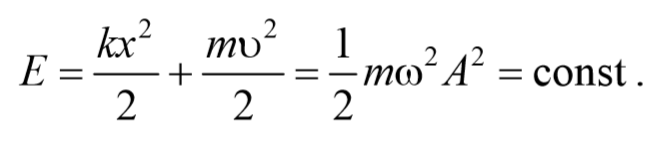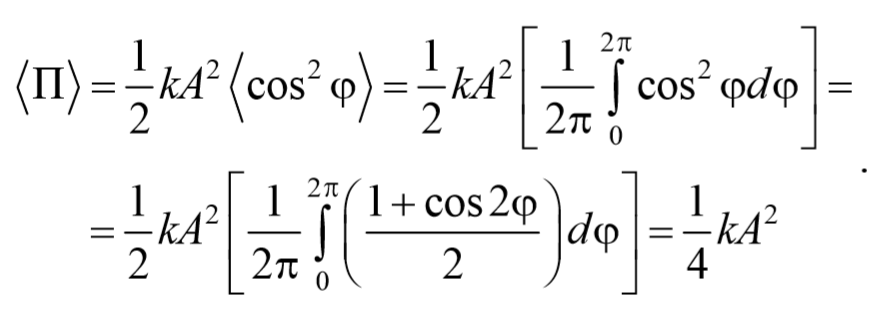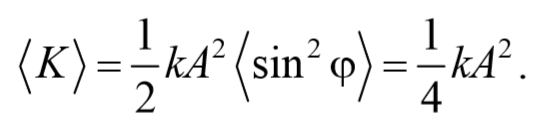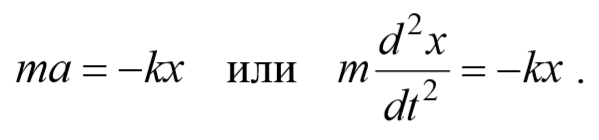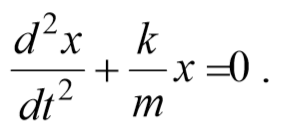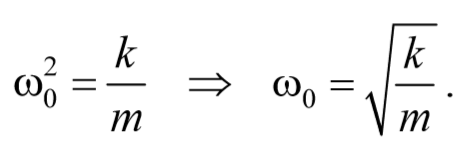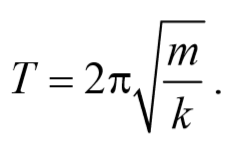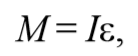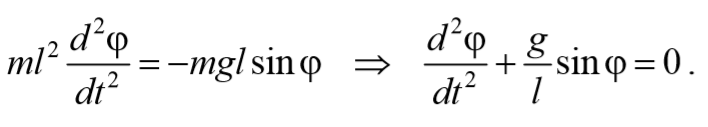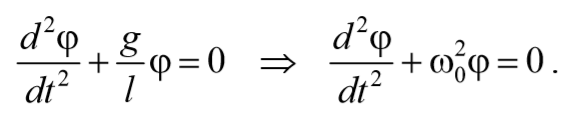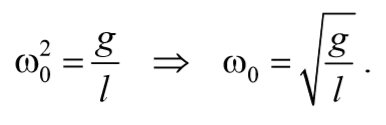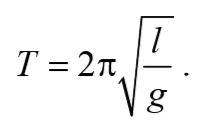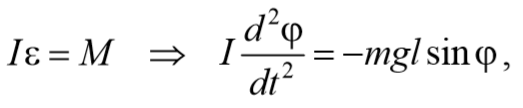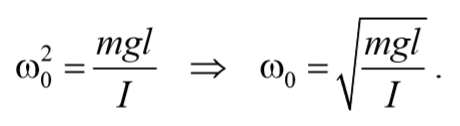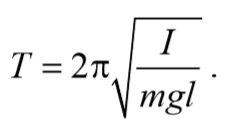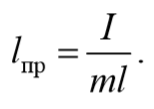Решение уравнения свободных механических колебаний

5.1. Свободные гармонические колебания и их характеристики.

Колебания − это движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебания, повторяются через равные промежутки времени. Наиболее важными характеристиками колебания являются: смещение, амплитуда, период, частота, циклическая частота, фаза.

Простейший вид периодических колебаний − это гармонические колебания. Гармонические колебания − это периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса. Уравнение гармонических колебаний имеет вид

1) Смещение x − это величина, характеризующая колебания и равная отклонению тела от положения равновесия в данный момент времени.

2) Амплитуда колебаний А − это величина, равная максимальному отклонению тела от положения равновесия.

3) Период колебаний T − это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Единица измерения [T] = 1 с .

За период система совершает одно полное колебание.

4) Частота колебаний ν − это величина, равная числу колебаний, совершаемых в единицу времени (за 1 секунду). Единица измерения [ν]= 1 Гц . Частота определяется по формуле

5) Циклическая частота ω − это величина, равная числу полных колебаний, совершающихся за 2π секунд. За единицу циклической частоты принята угловая частота, при которой за время 1 с совершается 2π циклов колебаний, [ω]= с -1 . Циклическая частота связана с периодом и частотой колебаний соотношением

6) Фаза колебаний ωt + φ₀ − фаза указывает местоположение колеблющейся точки в данный момент времени.

7) Начальная фаза φ₀ − указывает местоположение колеблющейся точки в момент времени t = 0 .

5.2. Сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний.

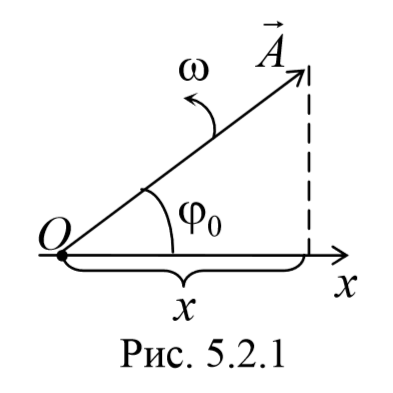
Сложение нескольких колебаний одинакового направления можно изображать графически с помощью метода векторной диаграммы.

Гармоническое колебание может быть представлено графически с помощью вращающегося вектора амплитуды А . Для этого из произвольной точки O , выбранной на оси Ox , под углом φ₀ , равным начальной фазе колебания, откладывается вектор амплитуды А . Модуль этого вектора равен амплитуде рассматриваемого колебания. Если этот вектор привести во вращение с угловой скоростью ω , равной циклической частоте колебаний, то проекция конца вектора амплитуды будет перемещаться по оси Ox и принимать значения от -A до +A , а колеблющаяся величина изменяться со временем по закону x = Acos(ωt + φ₀)

1. Сложение одинаково направленных гармонических колебаний.

Сложим два гармонических колебания одинакового направления и одинаковой частоты. Смещение x колеблющегося тела будет суммой смещений x₁ и x₂ , которые запишутся следующим образом:

Представим оба колебания на векторной диаграмме. Построим по правилу сложения векторов результирующий вектор А . Проекция этого вектора на ось Ox равна сумме проекций слагаемых векторов x=x₂+x₂ , следовательно, вектор А представляет собой результирующее колебание. Определим результирующий вектор амплитуды А потеореме косинусов

Так как угол между векторами А ₁ и А ₂ равен φ=π-(φ₂-φ₁) , то cos[π-(φ₂-φ₁)]=-cos(φ₂-φ₁) , следовательно, результирующая амплитуда колебания будет равна

Определим начальную фазу результирующего колебания.

Из рисунка видно, что начальная фаза результирующего колебания

Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, также совершает гармонические колебания в том же направлении и с той же частотой.

2. Сложение взаимно перпендикулярных гармонических колебаний.

Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты, происходящих во взаимно перпендикулярных направлениях. Допустим, что материальная точка совершает колебания как вдоль оси X , так и вдоль оси Y . Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний примут вид

где φ − разность фаз обоих колебаний.

Уравнение траектории получим, исключив из уравнений (5.2.6) параметр времени t: cosωt= $$xover A_1$$ , а sinωt= $$sqrt=sqrt$$ Разложим косинус во втором из уравнений (5.2.6)

Перепишем это уравнение в следующем виде

После преобразования, получим

Используя тригонометрическое тождество cos 2 φ+sin 2 φ=1 , окончательно получим

Это есть уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно. Ориентация эллипса и величина его полуосей зависят от амплитуд колебаний и разности фаз.

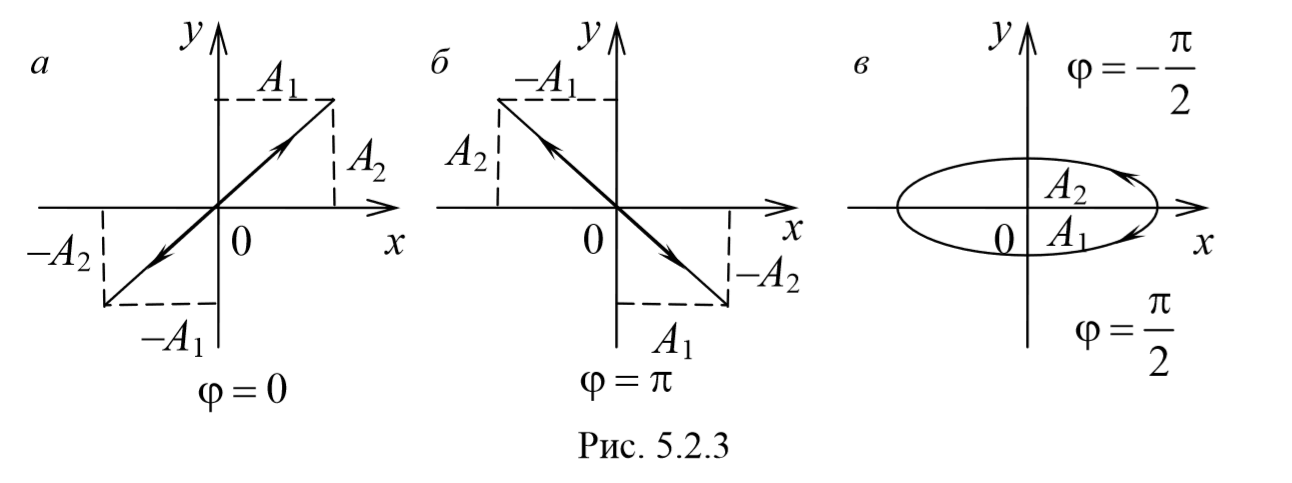
Рассмотрим несколько частных случаев и определим форму траектории для них:

a) разность фаз равна нулю [φ=0]

В этом случае $$( — )^2=0$$ , откуда получается уравнение прямой

Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой $$A= sqrt<A_1+A_2>$$ .

2) разность фаз равна ±π[φ=±π] .

В этом случае $$( — )^2=0$$ , откуда получается уравнение прямой

3) Разность фаз равна ± $$πover 2$$ [φ=± $$π over2$$ ] . Тогда

Уравнение эллипса, причем полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд колебаний эллипс вырождается в окружность. Случаи φ=+ $$πover 2$$ и φ=- $$πover 2$$ отличаются направлением движения. Если φ=+ $$πover 2$$ , то уравнения колебаний имеют следующий вид: x=A₁cosωt , и y=-A₂sinωt и движение совершается по часовой стрелке. Если φ=- $$πover 2$$ , , то уравнения колебаний имеют следующий вид: x=A₁cosωt , и y=A₂sinωt и движение совершается против часовой стрелке.

Рассмотренные три частных случая представлены на рис. 5.2.3, а, б, в. Рис

4) Если частоты складываемых взаимно перпендикулярных колебаний различны, то траектория результирующего движения имеет вид сложных кривых, называемых фигурами Лиссажу . Форма этих кривых определяется соотношением амплитуд, частот и разности фаз складываемых колебаний.

На рис. 5.2.4 показаны фигуры Лиссажу, которые получаются при соотношении частот 1:2 и различной разности фаз колебаний.

По виду фигур можно определить неизвестную частоту по известной частоте или определить соотношение частот складываемых колебаний.

5.3. Дифференциальное уравнение гармонических колебаний и его решение.

Продифференцируем по времени уравнение гармонических колебаний

и получим выражение для скорости

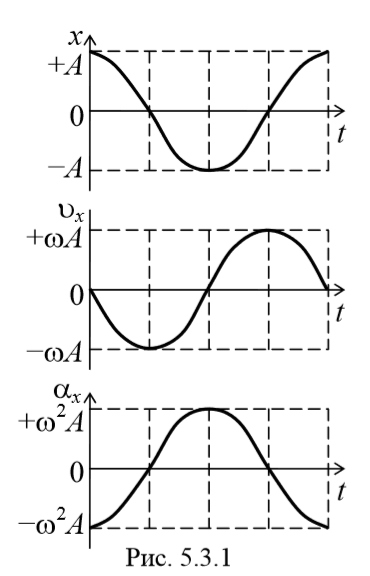
Из сравнения уравнений (5.3.1) и (5.3.2) следует, что скорость опережает смещение по фазе на π/2 . Амплитуда скорости равна Аω .

Продифференцировав уравнение (2) еще раз по времени, получим выражение для ускорения

Как следует из уравнения (5.3.3), ускорение и смещение находятся в противофазе. Это означает, что в тот момент времени, когда смещение достигает наибольшего, положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот. Амплитуда ускорения равна Аω 2 (рис. 5.3.1).

Из выражения (5.3.3) следует дифференциальное уравнение гармонических колебаний

Результирующая сила, действующая на материальную точку массой m , определяется с помощью второго закона Ньютона. Проекция этой силы

Эта сила пропорциональна смещению точки из положения равновесия и направлена в сторону противоположную этому смещению, т. е. она стремится вернуть точку в положение равновесия, и поэтому называется возвращающей силой . Таким образом, гармонические колебания происходят под действием силы F , пропорциональной смещению x и направленной к положению равновесия,

где k=mω 2 − постоянный коэффициент. Возвращающая сила подобна упругим силам, возникающим в телах при их деформации. Такая зависимость силы от смещения характерна для упругой силы, поэтому силы иной физической природы, удовлетворяющие зависимости (5.3.6) называются квазиупругими силами .

Материальная точка, совершающая колебания под действием квазиупругой силы, называется линейным осциллятором . Ее динамическое поведение описывается дифференциальным уравнением

ω₀ − собственная частота осциллятора.

Решение этого уравнения дает закон движения линейного осциллятора x=Acos(ωt+φ₀) .

5.4. Энергия гармонических колебаний.

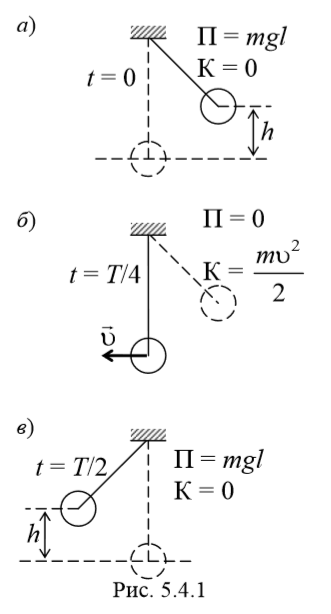
В процессе колебаний происходит превращение кинетической энергии в потенциальную энергию и обратно (рис. 5.4.1). В момент наибольшего отклонения от положения равновесия полная энергия состоит только из потенциальной энергии, которая достигает своего наибольшего значения. Далее при движении к положению равновесия потенциальная энергия уменьшается, при этом кинетическая энергия возрастает. При прохождении через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в этот момент достигает своего наибольшего значения. Далее при движении к точке наибольшего отклонения происходит уменьшение кинетической и увеличение потенциальной энергии. И при наибольшем отклонении потенциальная опять максимальная, а кинетическая энергия рана нулю. И т. д.

Потенциальная энергия тела, совершающего гармонические колебания равна

Кинетическая энергия тела, совершающего гармонические колебания равна

Таким образом, полная энергия гармонического колебания, состоящая из суммы кинетической и потенциальной энергий, определяется следующим образом

Следовательно, полная энергия гармонического колебания

оказывается постоянной в случае гармонических колебаний.

Найдем среднее значение потенциальной энергии за период колебания

Аналогично получается для среднего значение кинетической энергии

Таким образом, и потенциальная, и кинетическая энергии изменяются относительно своих средних значений по гармоническому закону с частотой 2ω и амплитудой ωt kA 2

5.5. Пружинный, математический и физический маятники.

Рассмотрим несколько простейших систем, совершающих свободные гармонические колебания.

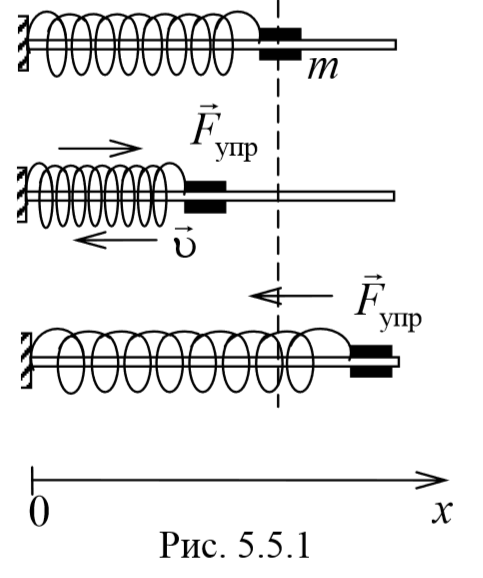
1) Пружинный маятник − это материальная точка массой m , подвешенная (или расположенная горизонтально) на абсолютно упругой пружине жесткостью k и совершающий гармонические колебания под действием упругой силы. Пусть шайба массой m , прикрепленная к пружине, совершает колебания. Для составления дифференциального уравнения колебаний запишем второй закон Ньютона в проекции на ось Ox F_упр=ma . Упругая сила F_упр=-kx . Приравнивая последние два уравнения и, используя определение ускорения тела, получим

Сравнивая уравнения (5.3.7) и (5.5.2) получаем, что пружинный маятник совершает гармонические колебания с частотой

Так как период колебаний определяется по формуле T= $$2πover ω_0$$ , то период колебаний пружинного маятника

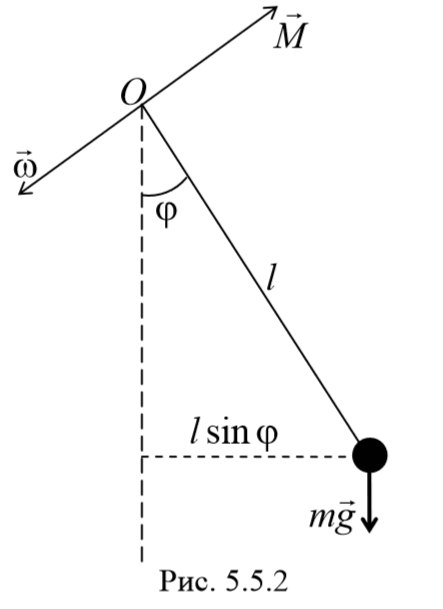
2) Математический маятник − это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена материальная точка массой m . Отклонение маятника от положения равновесия будем характеризовать углом φ , образованным нитью с вертикалью.

При отклонении маятника от положения равновесия возникает вращательный момент M , равный по величине mqlsinφ .Он имее акое же направление, что стремится вернуть маятник в положение равновесия. Следовательно, выражение для вращательного момента имеет вид: M=-mqlsinφ . Применим основно ательного движения

где L=ml 2 − момент инерции материальной точки. Тогда, учитывая, что угловое ускорение ε= $$d^2φover dt^2$$ , получим

Если рассматривать малые колебания, то sinφ≈φ . Получим

То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой

Период колебаний математического маятника

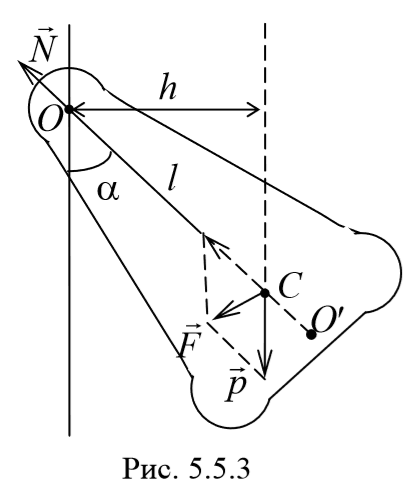
3) Физический маятник − это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, проходящей через точку, не совпадающую с центром масс тела. При отклонении маятника от положения равновесия на угол φ возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен M=-mglsinφ .

Согласно основному уравнению динамики вращательного движения получаем

где I − момент инерции маятника относительно оси, проходящей через точку подвеса.

Если рассматривать малые колебания, то sinφ≈φ . Получим

То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой

Период колебаний математического маятника

Из сопоставления формул периодов колебаний математического и физического маятников T=2π $$sqrt$$ и T=2π $$sqrt$$ получается, что математический маятник с длиной

будет иметь такой же период колебаний, что и данный физический маятник.

Величина l_пр (отрезок OO′) называется приведенной длиной физического маятника − это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка на прямой, соединяющей точку подвеса с центром масс, и лежащая на расстоянии приведенной длины от оси вращения, называется центром качания (О′) физического маятника. Точка подвеса О и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Механические колебания.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.

Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.

Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.

Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.

Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.

Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.

Частота колебаний — это величина, обратная периоду: . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Гармонические колебания.

Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение . Основная задача механики в данном случае состоит в нахождении функции , дающей координату тела в любой момент времени.

Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.

Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.

Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:

Выясним смысл входящих в эту формулу величин.

Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому — амплитуда колебаний.

Аргумент косинуса называется фазой колебаний. Величина , равная значению фазы при , называется начальной фазой. Начальная фаза отвечает начальной координате тела: .

Величина называется циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное радиан: , откуда

Измеряется циклическая частота в рад/с (радиан в секунду).

В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1) :

График функции (1) , выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1 .

Рис. 1. График гармонических колебаний

Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.

Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить . Мы получаем закон косинуса:

График гармонических колебаний в этом случае представлен на рис. 2 .

Рис. 2. Закон косинуса

Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить . Получаем закон синуса:

График колебаний представлен на рис. 3 .

Рис. 3. Закон синуса

Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Уравнение гармонических колебаний.

Вернёмся к общему гармоническому закону (1) . Дифференцируем это равенство:

Теперь дифференцируем полученное равенство (4) :

Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :

Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:

C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:

-решением уравнения (7) является всякая функция вида (1) с произвольными ;

-никакая другая функция решением данного уравнения не является.

Иными словами, соотношения (6) , (7) описывают гармонические колебания с циклической частотой и только их. Две константы определяются из начальных условий — по начальным значениям координаты и скорости.

Видео:Урок 327. Гармонические колебанияСкачать

Пружинный маятник.

Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4 ). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .

Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рис. 4. Пружинный маятник

В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:

Если 0′ alt=’x>0′ /> (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и . Наоборот, если , то 0′ alt=’F_>0′ /> . Знаки и всё время противоположны, поэтому закон Гука можно записать так:

Тогда соотношение (8) принимает вид:

Мы получили уравнение гармонических колебаний вида (6) , в котором

Циклическая частота колебаний пружинного маятника, таким образом, равна:

Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:

Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10) .

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать

Математический маятник.

Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5 ). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

Рис. 5. Математический маятник

Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.

Запишем для маятника второй закон Ньютона:

и спроектируем его на ось :

Если маятник занимает положение как на рисунке (т. е. 0′ alt=’x>0′ /> ), то:

Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:

Итак, при любом положении маятника имеем:

Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11) :

Это — уравнение гармонических колебаний вида (6) , в котором

Следовательно, циклическая частота колебаний математического маятника равна:

Отсюда период колебаний математического маятника:

Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.

Видео:Выполнялка 53.Гармонические колебания.Скачать

Свободные и вынужденные колебания.

Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6 ).

Рис. 6. Затухающие колебания

Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).

Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:

В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7 .

Рис. 7. Резонанс

Мы видим, что вблизи частоты наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, , а амплитуда колебаний возрастает до бесконечности при .

Видео:Физика 11 класс (Урок№1 - Механические колебания.)Скачать

Свободные и вынужденные механические колебания

Вы будете перенаправлены на Автор24

Движения или процессы, которые имеют определенную повторяемость, называют колебаниями.

Физическая природа колебаний может быть различной, в этой связи различают:

• механические колебания;
• электромагнитные колебания;
• квантовые;
• смешанные (электромеханические).

Разные по природе колебания описываю при помощи одинаковых параметров и одинаковых уравнений. Общим подходом исследования механических и электромагнитных колебаний пользовались разные ученые –физики, например, Д.У. Рэлеей и А.Г. Столетов, П.Н. Лебедев.

Видео:Физика 9 класс (Урок№9 - Механические колебания.)Скачать

Свободные гармонические колебания

Колебания считают свободными (собственными) в том случае, если они выполняются только за счет энергии, которая была сообщена колебательной системе в начальный момент времени и далее внешние воздействия на эту систему отсутствуют.

Самым простым для математического описания видом колебательных процессов стали гармонические колебания.

Гармоническими колебаниями называют колебания, у которых изменение колеблющегося параметра происходит по закону синуса или косинуса:

$s=s_m cos (omega_0 t+varphi) (1),$

где $s_m$ — наибольшее значение переменного параметра $s$ (амплитуда); $omega_0$ — циклическая частота колебаний; $varphi$ — начальная фаза колебаний; $(omega_0 t+varphi)$ — фаза колебаний в момент времени $t$. $- s_m

Гармонические колебания рассматриваются подробно поскольку:

1. колебания, которые происходят в реальной действительности часто близки к гармоническим;
2. разные периодические процессы можно представлять как сумму гармонических колебаний.

Состояния колебательной системы, выполняющей гармонические колебания, повторяются спустя промежуток времени, который именуют периодом колебаний ($T$). За время, равное периоду, фаза колебаний изменяется на величину, равную $2pi$:

Готовые работы на аналогичную тему

$(omega_0 (t+T)+varphi)=(omega_0 t+varphi)+2pi (2)$,

в результате можем записать:

Величину, обратную периоду, называют частотой колебаний:

Частота – это физическая величина, равная количеству полных колебаний которое система совершает за единицу времени. При этом выполняется равенство:

$omega_0 = 2pi nu (5).$

Видео:Уравнения механических колебанийСкачать

Дифференциальные уравнения свободных гармонических колебаний

Поведем дифференцирование по времени выражения (1), тогда первая производная равна:

$frac

=-s_m omega_0^2 cos (omega_0 t +varphi + pi)$(7).

В выражении (6) мы получили скорость колебаний, в (7) ускорение. Данные параметры движения колеблются с той же циклической частотой и амплитудами равными:

$v_m=s_m omega_0$; $a_m= s_m omega_0^2$.

Из формулы (6) мы видим, что фаза скорости отлична от фазы смещения $s$ на $frac$, тогда как фаза ускорения смещена на $pi$. Это означает то, что в тот момент времени, когда смещение равно нулю ($s=0$), скорость наибольшая. Если $s$ максимально и отрицательно, то ускорение имеет наибольшую положительную величину.

Из выражений (1) и (7) легко сделать вывод о том, что дифференциальное уравнение свободных гармонических колебаний записывается в виде:

Решением данного уравнения служит $s(t)$ вида (1).

Видео:ЧК_МИФ РЕШЕНИЕ УРАВНЕНИЯ СВОБОДНЫХ КОЛЕБАНИЙ В СЛУЧАЕ ОТСУТСТВИЯ ДИССИПАТИВНЫХ СИЛСкачать

Затухающие колебания

В реальной действительности любые свободные колебания являются затухающими.

Колебания называют затухающими, если их амплитуда в результате энергетических потерь с течением времени уменьшается.

Самым простым механизмом уменьшения энергии в колебательной системе является ее трансформация в тепловую энергию, в результате наличия сил трения.

Формула, которая описывает затухание колебаний, определена свойствами системы, выполняющей движения.

Дифференциальное уравнение свободных затухающих колебаний линейной системы можно представить в виде:

где $delta$ — коэффициент затухания; $omega_0$ — круговая частота свободных незатухающих колебаний этой же колебательной системы (если $delta =0$) называется собственной частотой.

Если затухание колебаний мало ($delta^2 ll omega_0^2$), то решением дифференциального уравнения (9) является функция вида:

$s=s_0 e^ cos (omega t +varphi) (10),$

где $omega = omega_0^2-delta^2$; $s_0=s_m e^$ — амплитуда колебаний при их затухании ($s_m $- начальная амплитуда).

Строго говоря, затухающие колебания нельзя отнести к периодическим. К ним нельзя применять понятия:

Иногда при очень малом затухании понятие период используют для обозначения отрезка времени между парой соседних максимумов (минимумов) параметра колебания. В этом случае период затухающих колебаний вычисляют как:

Конечным результатом эволюции колебательной системы с затухающими колебаниями является стремление ее к состоянию равновесия. Данное поведение понятно, поскольку связано с потерей энергетического запаса на совершение работы против сил трения в механической системе.

Видео:Превращение энергии при колебаниях. Уравнение колебательного движения. 1 часть. 9 класс.Скачать

Вынужденные колебания

Вынужденными называют колебания, если на колебательную систему происходит периодическое воздействие внешней силы (имеется источник энергии).

Вынужденными механическими колебаниями можно назвать звуковую волну, которая распространяется в веществе при наличии источника звука.

Для получения в реальной системе незатухающих колебаний, следует компенсировать потери энергии. Данная компенсация возможна при действии, например, периодического фактора $X(t)$, который изменяется в соответствии с законом:

$X(t)=X_0 cos (omega t)(12).$

При механических колебаниях вместо $X(t)$ можно записать внешнюю вынуждающую силу:

$F=F_0 cos (omega t) (13).$

Рассмотрим колебания тела на упругой пружине. Уравнением его колебаний будет:

где $r$ — коэффициент сопротивления; $omega_0 = sqrt<frac>$; $k$ — коэффициент упругости пружины; $m$ — масса тела на пружине. Коэффициент затухания при этом равен:

Уравнения вынужденных колебаний с учетом (13) запишем в виде:

$m ddot =-kx-rdot+F_0 cos (omega t) (16).$

$ddot +2delta dot +omega_0^2x=frac cos (omega t) (17).$

Уравнение (17) — это линейное неоднородное дифференциальное уравнение.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 17 05 2021

🎬 Видео

Урок 343. Затухающие колебания (часть 1)Скачать

5.4 Уравнение гармонических колебанийСкачать

Колебательное движение. 1 часть. 9 класс.Скачать

Урок 347. Вынужденные колебания. Резонанс (часть 1)Скачать

КОЛЕБАНИЯ физика 9 класс решение задачСкачать

Как решить уравнение колебаний? | Олимпиадная физика, механические гармонические колебания, 11 классСкачать

Урок 325. Колебательное движение и его характеристикиСкачать