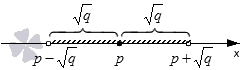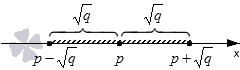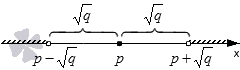Решение уравнения способом выделения квадрата двучлена (3 видео)

Решение квадратных уравнений с помощью выделения квадрата двучлена

Уравнениям вида , где а0, в школьном курсе математики придаётся большое значение. Анализируя работы учеников, можно прийти к выводу, что при решении квадратных уравнений учащиеся в 90% случаях используют формулу «дискриминанта», а на остальные 10% приходится графический способ, теорема Виета и с помощью разложения на множители. Многие ребята не знают другие приемы решения квадратных уравнений. Рассмотрим подробнее способы решения квадратных уравнений.

Решение квадратных уравнений с помощью выделения квадрата двучлена.

Рассмотрим на примере решение квадратного уравнения, в котором оба коэффициента при неизвестных и свободный член отличны от нуля. Такой способ решения квадратного уравнения называют выделением квадрата двучлена.

Рассмотрим уравнение

Разделив обе части этого уравнения на 7, получим равносильное ему приведенное квадратное уравнение . Выделим из трехчлена квадрат двучлена. Для этого разность представим в виде , прибавим к ней выражение и вычтем его. Получим .

Решая это уравнение получим два корня x=-, и x= 1.

Решение квадратных уравнений по формуле.

Умножим обе части уравнения

ах2 + bх + с = 0, а ≠ 0

на 4а и последовательно имеем:

4а2х2 + 4аbх + 4ас = 0,

((2ах)2 + 2ах • b + b2) — b2 + 4ac = 0,

(2ax + b)2 = b2 — 4ac,

2ax + b = ± √ b2 — 4ac,

2ax = — b ± √ b2 — 4ac,

Решение уравнений с использованием теоремы Виета. 4. СПОСОБ:

Как известно, приведенное квадратное уравнение имеет вид

Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид

Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).

а) Если свободный член q приведенного уравнения (1) положителен (q 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р, то оба корня отрицательны, если р, то оба корня положительны.

б) Если свободный член q приведенного уравнения (1) отрицателен (q ), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p, или отрицателен, если p 0 .

Решение уравнений с использованием теоремы Виета (обратной) Справедлива теорема, обратная теореме Виета:

Если числа х1 и х2 таковы, что х1+х2 = — р, х1х2 = q, то х1 и х2 – корни квадратного уравнения х2 +рх + q = 0.

Эта теорема позволяет в ряде случаев находить корни квадратного уравнения без использования формулы корней.

Решение уравнений способом «переброски».

Рассмотрим квадратное уравнение ах2 + bх + с = 0, где а ≠ 0.

Умножая обе его части на а, получаем уравнениеа2х2 + аbх + ас = 0.

Пусть ах = у, откуда х = у/а; тогда приходим к уравнению у2 + by + ас = 0,

равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета.

Окончательно получаем х1 = у1/а и х1 = у2/а. При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Свойства коэффициентов квадратного уравнения.

А. Пусть дано квадратное уравнение ах2 + bх + с = 0, где а ≠ 0.

1) Если, а+ b + с = 0 (т. е. сумма коэффициентов равна нулю), то х1 = 1, х2 = с/а.

Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение

x2 + b/a • x + c/a = 0.

Согласно теореме Виета

По условию а – b + с = 0, откуда b = а + с. Таким образом,

x1 + x2 = — а + b/a= -1 – c/a,

т. е. х1 = -1 и х2 = c/a, что м требовалось доказать.

Б. Если второй коэффициент b = 2k – четное число, то формулу корней

В. Приведенное уравнение х2 + рх + q= 0

совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней

Формулу (3) особенно удобно использовать, когда р — четное число.

Графическое решение квадратного уравнения.

Если в уравнении х2 + px + q = 0 перенести второй и третий члены в правую часть, то получим х2 = — px — q.

График первой зависимости — парабола, проходящая через начало координат. График второй зависимости – прямая. Возможны следующие случаи:

— прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;

— прямая и парабола могут касаться (одна общая точка), т. е. уравнение имеет одно решение;

— прямая и парабола не имеют общих точек, т. е. квадратное уравнение не имеет корней.

Решение квадратных уравнений с помощью циркуля и линейки.

рафический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.

Существует следующий способ нахождения корней квадратного уравнения ах2 + bх + с = 0с помощью циркуля и линейки

Допустим, что искомая окружность пересекает ось абсцисс в точках В(х1; 0 ) и D (х2; 0),где х1 и х2 — корни уравнения ах2 + bх + с = 0, и проходит через точки А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х1х2/ 1 = c/a.

ентр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому

1) построим точки S(-b/2а; (а+с)/2а) (центр окружности) и A(0; 1);

2) проведем окружность с радиусом SA;

3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.

При этом возможны три случая.

1) Радиус окружности больше ординаты центра (AS SK, или R a + c/2a), окружность пересекает ось Ох в двух точках (рис. 6,а) В(х1; 0) и D(х2; 0), где х1 и х2 — корни квадратного уравнения ах2 + bх + с = 0.

) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис. 6,б) в точке В(х1; 0), где х1 — корень квадратного уравнения.

3) Радиус окружности меньше ординаты центра

окружность не имеет общих точек с осью абсцисс (рис.6,в), в этом случае уравнение не имеет решения.

Решение квадратных уравнений с помощью номограммы.

Это старый и незаслуженно забыты способ решения квадратных уравнений, помещенный на с.83 (см. Четырехзначные математические таблицы. — М., Просвещение, 1990).

Таблица XXII. Номограмма для решения уравнения z2 + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициен-

там определить корни уравнения.

Криволинейная шкала номограммы построена

Полагая ОС = р, ED = q, ОЕ = а (все в см.), из

подобия треугольников САН и CDF получим пропорцию

откуда после подстановок и упрощений вытекает уравнение

z2 + pz + q = 0,причем буква z означает метку любой точки криволинейной шкалы.

Способ решения квадратных уравнений по теореме Безу.

При делении P(х) на х — в остатке может получиться лишь некоторое число r (если r = 0, то деление выполняется без остатка):P(x) = (x — ) Q (x) + r. (1)

Чтобы найти значение r, положим в тождестве (1) х = . При этом двучлен х — обращается в нуль, получаем, что P () = r.

Итак, доказано утверждение, называемое теоремой Безу.

Теорема 1 (Безу). Остаток от деления многочлена P(x) на двучлен х — равен P() (т. е. значению P(x) при х = ).

Если число является корнем многочлена P(x), то этот многочлен делится на х — без остатка.

Разделим р(х) на (х-1)

х-1=0; х=1, или х-3=0, х=3; Ответ: х1=2, х2=3.

Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств.

Однако, значение квадратных уравнений заключается не только в изяществе и краткости решения задач, хотя и это весьма существенно. Не менее важно и то, что в результате применения квадратных уравнений при решении задач не редко обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений.

1. Четырехзначные математические таблицы для средней школы. Изд. 57-е. — М., Просвещение, 1990. С. 83.

2. Квадратичные функции, уравнения и неравенства. Пособие для учителя. — М., Просвещение, 1972.

3. Решение квадратного уравнения с помощью циркуля и линейки. — М., Квант, № 4/72. С. 34.

4. Сборник задач по алгебре и элементарным функциям. Пособие для учителя. Изд. 2-е. — М., Просвещение, 1970.

Содержание

Тема урока: «Решение квадратных уравнений выделением квадрата двучлена». 8-й класс
Решение квадратных неравенств через выделение квадрата двучлена
Основа метода выделения квадрата двучлена
Как преобразовать исходное равенство в (x−p) 2 , ≥)
Решение полученного неравенства (x−p) 2 , ≥)
Решение при q, меньшем 0
Решение при q, равном 0
Решение при q, большем 0
🌟 Видео

Видео:Метод выделения полного квадрата. 8 класс.Скачать

Тема урока: «Решение квадратных уравнений выделением квадрата двучлена». 8-й класс

Разделы: Математика

Класс: 8

Цели урока:

освоить способ выделения квадрата двучлена из квадратного трехчлена, заданного в стандартном виде; конструировать решения квадратного уравнения способом выделения квадрата двучлена;
воспитывать познавательную активность, чувства ответственности и товарищества, культуры общения;
развивать логическое мышление для сознательного восприятия учебного материала

Оборудование:

план,
проектор,
компьютерная презентация,
учебное пособие «Алгебра-8» под редакцией Теляковского С.А.,
дидактические материалы по алгебре для 8 класса (В. И. Жохов, Ю. Н. Макарычев, Н. Г. Миндюк),
таблицы устных упражнений,
карточки-задания,
исторические сведения,
стенгазета,
алгоритм решения квадратного уравнения выделением квадрата двучлена, магнитофон.

I . Ориентировочно-мотивационный этап

Проверка домашнего задания через консультантов. Актуализация знаний.

Выполнение заданий творческого характера на доске.

1) (2 – 5х) 2 = 9 (Ответ: – 0,2; 1.)

2) х 2 – 4 | х | = 0,
| х | = а, а > 0,
а 2 – 4а = 0,
а(а – 4) = 0, а = 0 или а – 4 = 0,
а = 4,

| x | = 0, х = 0, | x | = 4, х = 4 или х = – 4. Ответ: – 4; 0; 4.

3) | 3x 2 + 5x – 4 | = 3x 2 + 4

3х 2 + 4 > 0 верно при любых значениях переменной х

а) 3х 2 + 5х – 4 = 3х 2 + 4, б) 3х 2 + 5х – 4 = – 3х 2 – 4,
5х = 8, х = 1,6 6х 2 + 5х = 0, х(6х + 5) = 0, х = 0, х = –
Устная работа. Теоретическая изюминка (презентация)

1) Какие уравнения вы знаете? (Линейные, квадратные)
2) Определение квадратного уравнения. Почему а ≠ 0?
3) Вспомните классификацию квадратных уравнений ( полные ,неполные , приведенные)
4) Какое уравнение называется неполным? Виды неполных квадратных уравнений.
5) Сколько корней имеет неполное квадратное уравнение каждого вида?
6) Д/м, стр. 23, 1,2 задание
7) (а + в) 2 = а 2 + 2ав + в 2 – квадрат суммы двух выражений . Замените * одночленом так, чтобы получившееся равенство было тождеством:
а) ( * + 2в ) 2 = а 2 + 4ав + 4в 2
б) (15 + * ) 2 = 225у 2 + 1 2х 3 у + 0,16х 6
в) (3а – 2,5в) 2 = 9а 2 + 6,25в 2 – *

II. Операционально-исполнительный этап

Определение приведенного квадратного уравнения:

Квадратное уравнение ах 2 + вх + с = 0 с первым коэффициентом а = 1 называется приведенным

1) Определите вид уравнения х 2 + 2х + 1= 0 и решите это уравнение

(х + 1) 2 = 0,
х + 1= 0, х = – 1.

– Каким способом вы решили?

2) Нельзя ли решить уравнение х 2 + 6х – 7 = 0 таким же способом? (Ответ учащихся: «Нужно выделить квадрат двучлена» )
– Сформулируйте учебную задачу нашего урока. (Ответ учащихся: «Учебная задача урока «Решение квадратного уравнения выделением квадрата двучлена» )
– Итак, мы определили задачу нашего урока: научиться решать квадратные уравнения выделением квадрата двучлена.

3) Выделите квадрат двучлена: х 2 + 6х – 7 = х 2 + 2х * 3 + 9 – 9 – 7 = (х + 3) 2 – 16

4) Решите уравнение

х 2 + 6х – 7 = 0,
(х + 3) 2 – 16 = 0, (х + 3) 2 = 16
х + 3 = 4 или х + 3 = – 4
х = 1 или х = – 7
Ответ: – 7; 1.

Проговаривание способа решения уравнения.

Алгоритм решения квадратных уравнений выделением квадрата двучлена (презентация)

а) определяем первое выражение;
б) находим второе выражение: выражение с переменной (т.е. удвоенное произведение двух выражений ) делим на удвоенное первое выражение
в) прибавим и отнимем квадрат второго выражения;
г) упростим выражения, выделив квадрат двучлена;
д) решаем как неполное квадратное уравнение.

5) Решите уравнение х 2 – 5х + 10 = 0,

х 2 – 2х* 5/2 + (5/2) 2 – (5/2) 2 + 10 = 0,
(х – 5/2 ) 2 = – 15/4, нет корней.

6) Ребята, как вы думаете, можно ли решить выделением квадрата двучлена следующее уравнение 2х 2 – 9х + 10 = 0, 5х 2 + 3х – 8 = 0? (Можно, но сначала надо разделить каждый член уравнения на 2 (5), так как а = 2 (а = 5))

а) х 2 – (9/2)х + 5 = 0, б) х 2 + (3/5)х – (8/5) = 0

Решите данные уравнения в парах.

(Проверка по образцу).

б) х 2 + 2х * 3/10 + 9/100 – 9/100 – 8/5 = 0,
(х + 3/10) 2 = 169/100,
| x + 3/10 | = 13/10,
х + 3/10 = 13/10 или х + 3/10 = –13/10,
х = 1 или х = – 1,6
Ответ: – 1,6; 1.

Проговаривание решения квадратного уравнения в парах.

Самостоятельная работа

а) х 2 – 4х + 4 = 0 , б) х 2 + 12х + 20 = 0
(х = 2) (х = – 2; х = – 10)

а) х 2 + 14х + 49 = 0, б) х 2 – 8х – 9 = 0
(х = – 7) (х = – 1; х = 9)

а) х 2 – х + = 0, б) 5y 2 – 6y + l = 0,
(х = ) (х = 1; х = )

а) у 2 – у + 1 = 0, б) 5х 2 – 8х + 3 = 0
(х = 2) (х = 1; х = 0,6 )

(Во время самостоятельной работы звучит классическая музыка) Взаимопроверка.
Учащиеся выставляют оценки карандашом.

Физминутка для глаз (компьютерная презентация)

7) При каком значении а уравнение х 2 + 12х + 36 = а имеет 2 корня, 1 корень, не имеет корней?
(х + 6) 2 = а при а > 0 , 2 корня ;
при а = 0, 1 корень;
при а 2 – 4х + 5 = m?
х 2 – 2х * 2 + 4 – 4 + 5 = m,
(х – 2) 2 + 1 = m,
(х – 2) 2 = m – 1,
при m > 1, 2 корня;
при m = 1, 1 корень.

9) Решите уравнение: у 2 – 4| y | – 96 = 0.
Пусть | y | = b, b > 0,
b 2 – 4b – 96 = 0,
b 2 – 2b* 2 + 4 – 4 – 96 = 0,
(b – 2) 2 = 100,
| b – 2 | = 10,
b – 2 = 10 или b – 2 = – 10,
b = 12 или b = – 8.
b = – 8 не удовлетворяет условию b > 0,
| у | = 12,
y = 12 или у = – 12.

Домашняя работа

№526 – обязательный уровень;
№528, С-24, №7 – повышенный уровень;

Творческая работа

а) Заполни «окошки» х 2 – 7х + 8 = (х – ∆) 2 + 8 – ∆ 2 2 и придумать самим такие задания.
б) Выделить квадрат двучлена из квадратного трехчлена ах 2 + вх + с = 0.

III. Рефлексивно-оценочный этап

– Что изучали на уроке?
– Как решали квадратные уравнения?
– Что вы знаете об истории возникновения квадратных уравнений?

Задачи на квадратные уравнения встречались уже в 499 году в Древней Индии. Часто они были в стихотворной форме. Вот одна из задач знаменитого индийского математика 12 века Бхаскары:

«Обезьянок резвых стая
Всласть поевши развлекалась,
Их в квадрате часть восьмая
На поляне забавлялась,
А 12 по лианам…
Стали прыгать, повисая,
Сколько было обезьянок,
Ты скажи мне, в этой стае?

Уже в то время он знал о двузначности корней квадратных уравнений (х/8) 2 + 12 = х.
Формулы решения квадратных уравнений в Европе были впервые изложены в «Книге абака», написанная в 1202 году итальянским математиком Леонардом Фибоначчи. И лишь в 17 веке , благодаря трудам Жирара, Декарта, Ньютона и других ученых , способ решения квадратных уравнений принимает современный вид , о котором мы с вами будем говорить на следующем уроке.

Видео:Выделение квадрата двучленаСкачать

Решение квадратных неравенств через выделение квадрата двучлена

Квадратные неравенства можно решать несколькими разными способами. Для лучшего понимания сути этих выражений полезно знать их все. Помимо привычного метода интервалов или графического способа существует и метод решения через выделение квадрата двучлена, о котором мы вам расскажем в данном материале.

Выделив квадрат двучлена в левой части, можно легко решить практически любое квадратное неравенство. Сейчас мы разберем данный метод по порядку, иллюстрируя каждый шаг решениями задач.

Видео:Решение КВАДРАТНЫХ УРАВНЕНИЙ. Выделение квадрата двучленаСкачать

Основа метода выделения квадрата двучлена

Для начала объясним основную суть данного подхода на примере условного квадратного неравенства a · x 2 + b · x + c 0 . Между выражениями при этом может стоять и знак ≤ , и ≥ , и > , это не принципиальный момент. Суть метода заключается в переходе от исходного неравенства к равносильному, которое имеет вид ( x − p ) 2 q ( ≤ , > , ≥ ) , при этом p и q могут быть произвольными числами. Для этого мы используем равносильные преобразования, подробно описанные в одной из предыдущих статей. По полученному равенству можно будет судить о решении исходного.

Теперь перейдем к объяснению следующих двух моментов: как именно привести заданное в условии равенство к нужному виду и как потом его нужно решать.

Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

Как преобразовать исходное равенство в (x−p) 2 , ≥)

Для этого нам нужно последовательно выполнить несколько шагов. Вот они:

Если мы имеем коэффициент a , который не равен 1 , то нам нужно разделить на него правую и левую часть равенства. Если он меньше 0 , то знак неравенства остается прежним, а если больше, то нужно поменять его на противоположный. В итоге у нас должно получиться равенство с коэффициентом при x 2 , которое будет равносильно исходному. Если коэффициент при x 2 равен единице, то первый шаг нужно пропустить.
Далее смотрим на коэффициент при x . Если он не равен нулю, то мы можем слева выделить нужный нам квадрат двучлена. Если же слагаемое с x в первой степени у нас отсутствует совсем, то этот шаг мы тоже пропускаем.
После этих действий нужно перенести оставшееся слагаемое-число направо с противоположным знаком.

Мы получили неравенство нужного нам вида. Разберем решения конкретных задач, чтобы увидеть преобразования на практике.

Допустим, у нас есть неравенство x 2 ≥ 0 . Видим, что коэффициент при x 2 – единица, значит, первый и второй шаги можно пропустить. Получается, что и на третьем шаге ничего не нужно переносить, ведь слагаемого-числа с левой стороны нет. Из этого заключаем, что имеющееся у нас неравенство уже имеет нужный нам вид ( x − p ) 2 ≥ q , только p = 0 и q = 0 .

Ответ: имеющееся у нас неравенство уже имеет нужный нам вид ( x − p ) 2 ≥ q

Возьмем пример чуть сложнее.

Так, у нас есть квадратное неравенство 5 · x 2 0 . Выполняем первый шаг, разделив обе части на старший коэффициент, равный пяти. Поскольку 5 больше нуля, знак равенства при этом не меняется. После этого неравенство приобретает вид x 2 0 , что соответствует нужным условиям при p = 0 и q = 0 . Два следующих шага можно пропустить.

Ответ: x 2 0

Если у нас есть квадратное неравенство — 3 · x 2 — 4 > 0 , то сначала мы должны выполнить деление обоих частей на — 3 . Поскольку делитель является отрицательным числом, то нужно будет поменять знак равенства на противоположный. У нас получится x 2 + 4 3 0 . Избавившись от иррациональности в знаменателе, запишем x 2 + 4 3 0 . Коэффициента при x у нас нет, поэтому второй шаг пропускаем. На последнем этапе переносим оставшийся свободный член вправо и получаем x 2 — 4 3 3 . Полученное равенство соответствует нужному нам виду ( x − p ) 2 q , причем p = 0 , и q = — 4 3 3 .

Ответ: x 2 — 4 3 3

Разберем преобразование неравенства 1 3 x 2 + 2 · x + 3 ≤ 0 . Первым делом разделим обе части на одну треть. Это действие аналогично умножению на три. Сохранив знак неравенства, получим x 2 + 6 · x + 9 ≤ 0 . Поскольку слагаемое с x у нас есть, нам нужно выделить квадрат двучлена: ( x + 3 ) 2 ≤ 0 . Последний шаг мы не выполняем, поскольку числового слагаемого не осталось. Таким образом, мы заменили исходное квадратное неравенство на равносильное ему ( x − p ) 2 ≤ q , где p = − 3 и q = 0 .

Ответ: ( x + 3 ) 2 ≤ 0

Посмотрим еще один пример с квадратным неравенством 4 · x 2 − 4 · x − 1 0 . Начнем с деления на коэффициент при x 2 , т.е. на четыре. У нас получится x 2 — x — 1 4 0 . Выделяем квадрат двучлена: x 2 — 2 · 1 2 · x + 1 2 2 — 1 2 2 — 1 4 0 и далее x — 1 2 2 — 1 2 0 . Осталось перенести оставшееся свободное слагаемое в правую часть с другим знаком. Итоговое равносильное неравенство имеет вид x — 1 2 2 1 2 , где p = 1 2 , q = 1 2 .

Ответ: x — 1 2 2 1 2

Видео:Как решать квадратные уравнения методом выделения квадрата двучлена. Алгебра 8 классСкачать

Решение полученного неравенства (x−p) 2 , ≥)

Мы разобрали, как правильно преобразовывать имеющиеся неравенства для приведения их к исходному виду. Далее рассмотрим, как найти их решение. Разберем три основных случая, когда q больше 0 , меньше 0 или равно 0 .

Видео:Полный квадрат. Где и когда он может пригодиться? | Математика TutorOnlineСкачать

Решение при q, меньшем 0

В этом случае в основе решения лежит свойство степени: любое число, возведенное в квадрат, является неотрицательным. Мы помним также, что квадрат числа, не равного нулю, всегда положителен, а квадрат нуля равен 0 только в том случае, если 0 лежит в основании степени. В буквенном виде это можно записать как d 2 ≥ 0 для любого d , d 2 > 0 при любом d ≠ 0 , и d 2 = 0 только тогда, когда d = 0 .

Допустим, что в основании лежит отрицательное число. Значение ( x − p ) 2 , согласно указанным выше свойствам квадрата, не может быть отрицательным. Следовательно, будут справедливы неравенства ( x − p ) 2 p и ( x − p ) 2 ≤ p , причем x может быть любым. Таким образом, любое действительное число может считаться решением этих неравенств.

А вот ( x − p ) 2 p и ( x − p ) 2 ≤ p не будут справедливыми ни при каких значениях x . Из этого можно сделать вывод, что решений у них нет.

Условие: найдите решение квадратного неравенства x 2 + 4 · x + 5 > 0 .

Решение

Cначала нам нужно выделить полный квадрат с левой стороны.

x 2 + 2 · 2 · x + 2 2 − 2 2 + 5 > 0 , ( x + 2 ) 2 + 1 > 0

После этого переносим 1 вправо: ( x + 2 ) 2 > − 1 .

У нас получилось равенство, равносильное исходному. Для него любое действительное число может стать решением, поскольку выражение слева будет неотрицательным всегда, при любом значении x . То же можно сказать и о ( x + 2 ) 2 > − 1 . Значит, решением неравенства, заданного в условии, может быть любое действительное число.

Ответ: любое действительное число.

Условие: вычислите 9 · x 2 + 6 · x + 28 ≤ 0 .

Решение

Для данного квадратного неравенства подходит метод решения с помощью выделения квадрата двучлена. Для начала разделим левую и правую часть неравенства на девять и выделим нужный квадрат. У нас осталось одно слагаемое, которое надо перенести в правую часть с противоположным знаком.

x 2 + 2 3 · x + 28 9 ≤ 0 x 2 + 2 · 1 3 · x + 1 3 2 — 1 3 2 + 28 9 ≤ 0 x + 1 3 2 + 3 ≤ 0 x + 1 3 2 ≤ — 3

Выражение в левой части будет неотрицательным при любом значении x . Это значение также не может быть равно — 3 или быть меньше него. Получается, что итоговое равенство не имеет решения, следовательно, и исходное равенство, которое равносильно ему, также решений иметь не будет.

Ответ: решений у данного неравенства нет.

Видео:Выделение квадрата двучлена из квадратного трехчленаСкачать

Решение при q, равном 0

Допустим, что значение q равно 0 , тогда нам нужно рассмотреть неравенства ( x − p ) 2 0 , ( x − p ) 2 ≤ 0 , ( x − p ) 2 > 0 и ( x − p ) 2 ≥ 0 ) . Зная свойства числа, возведенного в квадрат, мы можем заключить, что значение ( x − p ) 2 будет больше нуля при таких значениях x , которые будут соответствовать условию x − p ≠ 0 , и будет равно нулю, если x − p = 0 .

( x − p ) 2 > 0 будет верным неравенством при таких значениях переменной x , когда x − p ≠ 0 , то есть при x ≠ p .
( x − p ) 2 ≥ 0 не будет верным равенством ни при одном действительном x , если x − p = 0 .

Условие: выясните, есть ли решения у квадратного неравенства − 0 , 2 · x 2 + 4 · x − 20 ≥ 0 .

Решение

Начнем с необходимых равносильных преобразований.

x 2 − 20 · x + 100 ≤ 0 ( x − 10 ) 2 ≤ 0 .

Получившееся в итоге равенство будет справедливым лишь в том случае, если x − 10 = 0 . Получается, что нужное нам значение x равно 10 . Следовательно, это число и будет единственным решением исходного неравенства.

Ответ: есть единственное решение 10 .

Условие: найти решение 16 · x 2 + 40 · x + 25 > 0 .

Решение

Начнем с деления на 16 , после чего нужно выделить квадрат двучлена.

x 2 + 5 2 · x + 25 16 > 0 x + 5 4 2 > 0 x + 1 1 4 > 0

Это неравенство имеет решения. Оно будет верным для всех значений x , за исключением такого, которое обратит основание степени в 0 , т.е. x ≠ — 1 1 4 .

Ответ: — ∞ , — 1 1 4 ∪ — 1 1 4 , + ∞

Видео:Выделение квадрата двучлена из квадратного трехчленаСкачать

Решение при q, большем 0

Последний случай, который нам нужно разобрать, – это решение неравенств ( x − p ) 2 q , ( x − p ) 2 ≤ q , ( x − p ) 2 > q и ( x − p ) 2 ≥ q при значении q больше 0 .

Для этого нам понадобится вспомнить другие свойства корня: неравенство u v ( ≤ , > , ≥ ) можно преобразовать в u v при любых положительных u и v ; для любого положительного t является верным равенство t 2 = t .

Первое свойство позволяет нам перейти от обычного квадратного неравенства к иррациональному, а второе – к неравенству с модулем. В обоих случаях полученные неравенства будут равносильными исходному.

Чтобы решить неравенство с модулем, нужно раскрыть этот модуль. Так, мы можем преобразовать x — p q в две системы неравенств без модуля x — p ≥ 0 x — p q и x — p 0 — x — p q . Покажем пример решения задачи.

Условие: вычислите x 2 − 6 · x − 7 > 0 , предварительно выделив квадрат двучлена.

Решение

Выделив нужный квадрат, получим x 2 − 2 · 3 · x + 3 2 − 3 2 − 7 > 0 , ( x − 3 ) 2 − 16 > 0 . Теперь перенесем слагаемое — 16 вправо с положительным знаком и получим ( x − 3 ) 2 > 16 . Теперь запишем равносильное ему иррациональное неравенство x — 3 2 > 16 ,далее | x − 3 | > 4 . Теперь преобразуем его в совокупность двух систем неравенств, чтобы избавиться от модуля.

x — 3 ≥ 0 x — 3 > 4 x — 3 0 — ( x — 3 ) > 4 x ≥ 3 x > 7 x 3 x — 1 x > 7 x — 1

У нас получилось, что решением исходного квадратного неравенства будет x − 1 , x > 7 .

Ответ: x − 1 , x > 7 .

Существует еще один удобный и наглядный способ решения неравенств x — p q ( ≤ , > , ≥ ) . С его помощью можно обойтись без введения систем. Для его применения необходимо понимать геометрический смысл модуля.

В рамках геометрических представлений модуль | x − p | представляет собой расстояние то точки с координатой x до точки с координатой p , отложенное по оси координат. Отсюда можно сделать следующие выводы:

Решениями неравенства x — p q будут координаты таких точек, расстояние от которых до точки с координатой p будет меньшим, чем значение q . См. на иллюстрацию:

Таким образом, данному неравенству будут удовлетворять значения переменных из интервала p — q , p + q .

Решением неравенства x — p ≤ q будут все те значения x , при которых расстояние от точки с координатой p будет меньше или равно q . Графически это можно представить так:

Следовательно, решением данного неравенства будут числа из интервала p — q , p + q

Если нам нужно найти решение x — p > q , то мы должны взять точки, расстояние от которых до точки p будет больше q . См. на иллюстрацию:

Решения данного неравенства будут лежат в интервале — ∞ , p — q ∪ p + q , + ∞ .

Вернемся к решению предыдущей задачи, чтобы наглядно показать эти выкладки.

Условие: найдите решения квадратного неравенства x 2 − 6 · x − 7 > 0 .

Решение: выполним все необходимые равносильные преобразования, выделив квадрат двучлена слева, и приведем исходное неравенство к нужному нам виду ( x − 3 ) 2 > 16 . Далее запишем:

( x — 3 ) 2 > 16 x — 3 > 4

Полученному неравенству будут удовлетворять координаты всех точек, расположенных от точки с координатой 3 на расстоянии больше 4 . Покажем на рисунке: