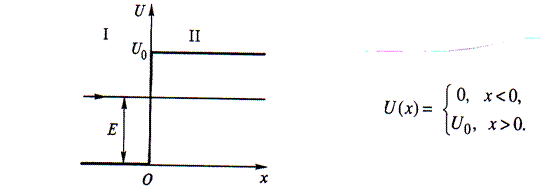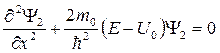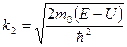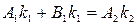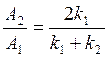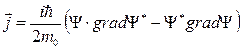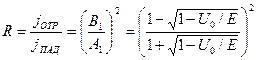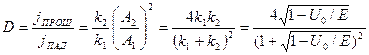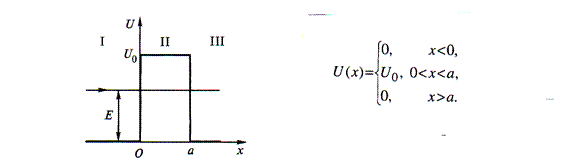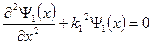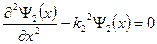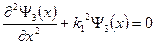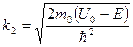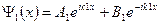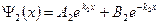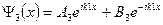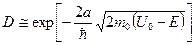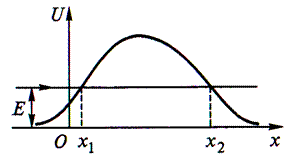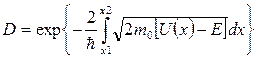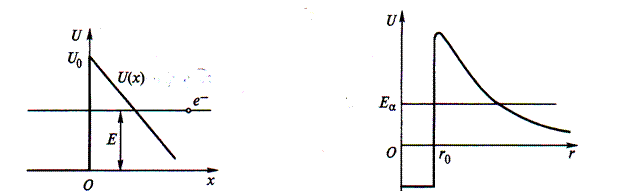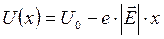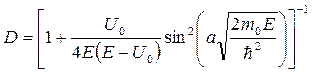Рассмотрим модель рассеяния электрона на потенциальном рельефе, описываемом следующим выражением:
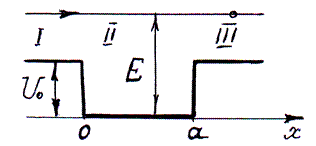
Рис. 1. Энергетическая диаграмма потенциальной ступеньки
Обозначим область слева от порога (x0) цифрой 1, справа от порога (x0) обозначим цифрой 2. Будем считать , что источник электронов находится в области 1 и бесконечно удален от границе раздела между областями 1 и 2.
Уравнение Шредингера для частицы в таком силовом поле имеет вид :

I. Рассмотрим сначала случай, когда энергия частицы E меньше высоты потенциального порога , т.е. .
Сделаем замену на :

Получаем уравнения Шредингера для областей 1 и 2 :
1) Решим уравнение Шредингера (6) для области 1:

Решение уравнения (6):
2) Решим уравнение Шредингера (7) для области 2:

Волновая функция представляет собой сумму падающей и отраженной волны де Бройля , — амплитуда волны, распространяющейся от источника электронов к потенциальной ступеньки , — амплитуда волны ,отраженной от потенциальной ступеньки.
В том, что выражение действительно описывает плоскую волну, легко убедиться, вспомнив про временной множитель для волновой функции в стационарном состоянии. Умножая на , получаем , т.е. плоскую волну де Бройля, распространяющуюся вдоль оси в положительном направлении. Аналогично, представляет плоскую волну де Бройля, распространяющуюся вдоль оси в отрицательном направлении.
Тогда как волновая функция , характеризующая движение частицы в области 2 , представляет собой сумму двух экспонент с действительными показателями степени. Учитывая однородность среды в области 2 (по постановке задачи в области 2 нет источников электронов и нет однородностей , от которых они могли бы отразиться ) и поскольку волновая функция должна быть ограниченной, а первое слагаемое в волновой функции при , неограниченно возрастает, то необходимо потребовать, чтобы коэффициент .
Решение уравнения Шредингера в области 2 можно записать в виде:
Далее, в силу того, что высота порога имеет конечную величину, волновая функция на границе раздела областей 1 и 2 должна быть не только непрерывной, но и гладкой, т.е. иметь непрерывную производную. Сшиваем волновые функции и их производные. В данном случае условия сшивки имеют вид:




Система уравнений (11) позволяет выразить коэффициенты и через коэффициент .











Таким образом, волновые функции частицы в случае высокого порога имеют вид:
Отметим, что система уравнений имеет решение при любых значениях коэффициентов и , т.е. при любых значениях энергии ( напомним, что). Это означает, что частица обладает непрерывным энергетическим спектром.
Найдем коэффициент отражения, определяющий вероятность того, что частица отразится от высокого порога. Согласно физическому смыслу, коэффициент отражения есть


где и — векторы плотности потока вероятности соответственно для падающей (первое слагаемое в ) и отраженной (второе слагаемое в) волн. Вектор плотности потока вероятности определяется через волновую функцию следующим образом:




Подставляя эти выражения в (15), находим, что
Коэффициент прохождения частицы через порог D , определяющий вероятность того, что частица пройдет в область II (коэффициент прозрачности порога) , имеет вид
где — вектор плотности потока вероятности для прошедшей волны . Подставляя в , получаем, что
а, следовательно и , и прошедшая волна.
Таким образом, в случае высокого порога
и выполняется условие: .
Рассмотрим поведение частицы в области II высокого потенциального порога. Волновая функция частицы отлична от нуля и спадает с по экспоненциальному закону, а это означает, что существует отличная от нуля вероятность пребывания частицы под порогом, т.е. в области, в которой полная энергия частицы меньше ее потенциальной энергии . С точки зрения классической механики эта область для частицы является запрещенной, т.к. условие означает, что кинетическая энергия частицы должна быть отрицательной. Однако, с точки зрения квантовой механики никакого противоречия здесь нет. Кинетическая энергия является функцией импульса частицы, а потенциальная энергия — функцией ее координаты, но, согласно соотношению неопределенностей, одновременное точное определение координаты и импульса невозможно. Поэтому в квантовой механике представление полной энергии частицы в виде суммы одновременно точно определенных кинетической и потенциальной энергий не имеет смысла.
Полученный результат означает, что микрочастицы могут проникать в области, которые для макроскопических частиц запрещены. Плотность вероятности нахождения частицы в области II определяется выражением
и зависит от эффективной массы частицы m , разности энергий и расстояния от границы порога , не зависит от времени .
Оценим величину экспоненциального множителя в для случая электрона, полагая эВ . При м , т.е. при расстоянии от порога, сравнимом с размерами атома,
Мы видим, что экспоненциальный множитель в этом случае имеет заметную величину, а это означает, что вероятность найти электрон на таком расстоянии в области II высокого потенциального порога достаточно велика. При м
что означает, что вероятность пребывания электрона на таком расстоянии от порога ничтожно мала. Полученные оценки показывают, что электрон с заметной вероятностью может проникать в область II лишь на расстояния, сравнимые с размером атома.
Таким образом, хотя коэффициент отражения частицы от высокого барьера , т.е. отражение является полным, оно не обязательно происходит на самом пороге, т.е. на границе раздела областей I и II . С определенной вероятностью частица может проникнуть в область II и затем выйти из нее.
Интересно отметить, что рассмотренное явление имеет аналог в классической физике — явление полного внутреннего отражения в волновой оптике. В этом случае также происходит полное отражение при падении света на границу раздела оптически более плотной и оптически менее плотной сред. При этом свет может проникать в оптически менее плотную среду, однако его амплитуда, как и , убывает с глубиной по экспоненциальному закону.
Перейдем теперь к анализу случая, когда энергия налетающей на порог частицы превышает высоту потенциального порога , т.е. . Такой порог носит название низкого потенциального порога. В этом случае уравнение Шредингера для областей I и II имеет вид
(22a)
(22b)
где и определяются соотношениями
Решая уравнения (22) , получаем
Будем считать, что частица приближается к порогу со стороны отрицательных значений , т.е. движется слева направо. При этом первое слагаемое в описывает падающую на порог волну де Бройля, а второе слагаемое в — волну, отраженную от порога. Аналогично, первое слагаемое в соответствует прошедшей через порог волне де Бройля. Поскольку отраженная волна в области II отсутствует, то коэффициент в (24b) следует положить равным нулю, т.е. .
Условие сшивки волновых функций и их производных на границе ( при ) приводит к следующим уравнениям для коэффициентов , и


Полагаем, как и в предыдущем случае :


Таким образом, волновые функции частицы в случае ее движения в области низкого порога имеют вид
где и заданы соотношениями (23) .
Для того, чтобы найти коэффициенты отражения и прохождения частицы через порог, найдем векторы плотности потока вероятности для падающей, отраженной и прошедшей (преломленной) волн де Бройля. Подставляя найденные волновые функции в (15), получаем





Коэффициент отражения частицы от низкого потенциального порога с учетом (27b), (28b) есть
Из (30) следует, что при существует отличная от нуля вероятность отражения частицы от низкого потенциального порога, т.е. возможно так называемое надбарьерное отражение. Этот результат является чисто квантовым и объясняется наличием у частицы волновых свойств. Макроскопическая частица, подчиняющаяся законам классической механики, при прохождении через низкий потенциальный порог не испытывает отражения, в области порога лишь уменьшается ее кинетическая энергия.
Интересно отметить, что если потенциальный порог «обратить», т.е. считать, что в области I и в области II , то коэффициент отражения останется прежним. В этом случае изменится лишь разность фаз между падающей и отраженной волнами де Бройля. Так, в рассматриваемом случае знаки амплитуд падающей и отраженной волн (первое и второе слагаемое в в выражении (14)) одинаковы, что соответствует разности фаз между волнами, равной нулю. В случае «обращенного» порога знаки амплитуд падающей и отраженной волн различны, что соответствует разности фаз, равной . Т.е. при отражении от «обращенного» порога фаза волны скачком меняется на продолжая аналогию с оптикой, можно сказать, что область I является для волны де Бройля оптически более плотной, чем область II .
Коэффициент прохождения частицы через порог, согласно (27b), (29b) , есть
Таким образом, и в случае низкого порога , что естественно было ожидать с точки зрения сложения вероятностей — падающая на порог частица либо отразится от него, либо пройдет в область II .
Следует отметить, что волна де Бройля, описывающая движение частицы в области порога, на границе раздела областей I и II испытывает преломление, связанное с изменением скорости частицы и ее волны де Бройля . Показатель преломления имеет вид


где и — дебройлевские длины волн, а и — скорости движения частицы соответственно в областях I и II . Выражая и через кинетическую энергию частицы, получаем
В рассматриваемом случае низкого порога ( ) , показатель преломления , что еще раз отражает тот факт, что область I является для частицы оптически более плотной средой, чем область II . В случае «обращенного» порога показатель преломления
оказывается больше единицы.
Анализ графического представления.
Вспоминаем для E 0 и E U0:
Рассмотрим плотность вероятности распределения частицы в 2 зонах:
Аналогично случаю для E U0 будет иметь вид косинусоиды (амплитуда которой зависит от и скорость изменения фазы- от ), приподнятой на некоторое значение, зависящее от и , где и заданы (смотри Рисунок 3).
Подставляем значения коэффициентов:

Следовательно, график плотности вероятности при x>0 и E>U0 будет иметь вид горизонтальной высота которой зависит от значений E и (смотри Рисунок 3).
1. Код программы
Программа представляет из себя набор из семи файлов. Файл Program.m — скрипт программы, который является главным и задействует функции. Файл WorkOkno.m — аналог Program.m с использованием графического интерфейса. WorkOkno.fig — графический интерфейс программы. RDgraphics.m , func1.m, func2.m -функции. Картинка используемая в графическом интерфейсе — image1.jpg. Ниже представлен рисунок с пояснением интерфейса и код программы.
электрон рельеф силовой поле
Рис.2 Интерфейс программы
%Programma modelirovaniya dvigeniya chastici v oblasti potencialnogo poroga
h=1.0546e-34; %Zadaem postoynnyu planka v Jouli na sekyndy
m0=0.911e-30; %Berem za massy chastici massy elektrona v kilogramax
eVvJ=1.6e-19; %Zaryad elektrona v Kylonax dlya perevoda iz elektronvolt v Jouli
U0_eV=input(‘U0= ‘); %Zadaem visoty potencialnogo poroga v elektronvoltax
E_eV=input(‘E= ‘); %Zadaem energiy chastici v elektronvoltax
x1=input(‘x1= ‘); %Zadaem oblast dvigeniya chastici, nachalnaya koordinata v nanometrax
x2=input(‘x2= ‘); %Zadaem oblast dvigeniya chastici, konechnaya koordinata v nanometrax
K1=input(‘K1= ‘); %Zadaem koefficent K1 dlya massi elektrona v pervoi oblasti
K2=input(‘K2= ‘); %Zadaem koefficent K2 dlya massi elektrona vo vtoroi oblasti
m1=m0*K1; %Massa elektrona v pervoi oblasti
m2=m0*K2; %Massa elektrona vo vtoroi oblasti
U0=U0_eV*eVvJ; %Perevod energii visoty potencialnogo poroga v Jouli
E=E_eV*eVvJ; %Perevod energii chastici v Jouli
x1=x1*10e-9; %Perevod nachalnoi koordinati v nanometri
x2=x2*10e-9; %Perevod konechnoi koordinati v nanometri
x1=linspace(x1,0,1000); %Formiryem lineinii massiv dlya oblasti menshe nylya
x2=linspace(0,x2,1000); %Formiryem lineinii massiv dlya oblasti bolshe nylya
Видео:Урок 455. Уравнение ШрёдингераСкачать

Потенциальный барьер бесконечной ширины. Уравнение Шредингера и его решение для случаев ЕU
Рассмотрим теперь одномерный потенциальный барьер бесконечной ширины (рис. 35.2), который по определению задается следующей зависимостью потенциальной энергии от координаты х:

Рассмотрим движение микрочастицы в таком поле, которое иногда также называют полем прямоугольной ступеньки. Если в классической физике частица с энергией Е Рис. 35.2 попадает (падает) слева па такой барьер, то
при Е > U она свободно пройдет над барьером, а при Е U отразиться от барьера, а при Е 0 (в области 2) при наличии потенциальной энергии стационарное уравнение Шредингера имеет вид
с общим решением
Общие решения этих дифференциальных уравнений можно представить, выразив энергию через импульс в виде
При этом v|/(_r) представляет собой только координатную часть волновой функции [i(x, /:) (34.10), которая должна быть дополнена зависящей от вре-
мени составляющей ехр —ht :
Из условия постоянства фазы очевидно, что первая составляющая волновой функции соответствует волне, распространяющейся в положительном направлении оси х (вправо): Et — рх = const, откуда с ростом времени t растет координатах. В свою очередь, вторая составляющая волновой функции соответствует волне, распространяющейся в отрицательном направлении оси х (влево): Et + рх = const, откуда с ростом времени t координата х убывает.
Для микрочастицы, летящей вправо из -°о, запишем, проанализируем и свяжем решения стационарного уравнения Шредингера в двух областях, учитывая возможности отражения микрочастицы от стенки барьера:
Здесь учтено, что в области 1 может существовать волна ( i I— «)
Б, ехр —v2 тЕх , отраженная от стенки барьера, а в области 2 отражен-
ной (движущейся влево) волны нет, поскольку не от чего отражаться.
Рассмотрим сначала случай, когда полная энергия частицы меньше высоты барьера: Е 0 отрицательна. В квантовой физике этот запрет снимается. Если Е Е U-E
энергии барьера над энергией частицы-. В результате можно выра-
зить амплитуду отраженной волны через амплитуду падающей волны:
Несложно убедиться, что модуль дроби в этом выражении равен единице:
откуда следует, что модуль амплитуды отраженной волны равен модулю амплитуды падающей волны. Это означает, что волна полностью отражается и коэффициент отражения волны при Е U. В классической физике такая частица свободно заходит в область барьера. Покажем, что в квантовой физике это не так. Для этого проведем сшивку функций (35.24), (35.26) с учетом условий (35.27) на стейке барьера х = 0:
Избавляясь в системе от А2, получим уравнение
где коэффициент г= —-— определяется относительным превышением
энергии частицы нал энергией оарьера-. В результате можно выра-
зить амплитуду отраженной и прошедшей волн через амплитуду падающей волны:
Найдем коэффициент прозрачности (прохождения) D потенциального барьера, определяемый как отношение плотности потока прошедших частиц к плотности потока падающих. Плотность потока микрочастиц равна произведению скорости частиц на их плотность vp. Скорость частиц в области 1 равна г = ^2Е/т, а в области 2 она равна v2 = yj2(E-U)/т. В свою очередь, плотность частиц пропорциональна квадрату амплитуды волны. В результате имеем для коэффициента прозрачности
Аналогично для коэффициента отражения от потенциального барьера, определяемого как отношение плотности потока отраженных частиц к плотности потока падающих (с учетом одинаковых скоростей), получаем формулу
Поскольку микрочастицы при взаимодействии с барьером никуда не исчезают и могут либо пройти барьер, либо отразиться, то выполняется естественное соотношение
При Е > U > 0 очевидно 0 Uс точки зрения классической физики энергию, существует вероятность отражения микрочастицы от барьера. При этом квантовый расчет показывает, что коэффициент прохождения равен единице только в случае г = 1 — только тогда, когда U = О и барьер попросту отсутствует. Кстати, последнее утверждение математически подтверждает ранее сделанное предположение о том, что отражение возможно лить на неоднородностях потенциала.
Следует сделать еще одно важное замечание по поводу того, что коэффициент отражения зависит лишь от энергии частицы и потенциальной энергии барьера, но не зависит от постоянной Планка и массы частицы. Формально это позволяет применить выведенную формулу для коэффициента отражения даже для бильярдного шара, что противоречит принципу соответствия и ньютоновой механике. Впрочем, это противоречие кажущееся. Классический предел в данной задаче подразумевает, помимо прочего, то, что длина волны де Бройля частицы мала по сравнению с характерным размером изменения потенциальной энергии. Это делает формальный переход к классике для вертикальной ступеньки потенциальной энергии некорректным.
Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Одномерный потенциальный порог и барьер
Движение частицы в области потенциального порога
Потенциальным порогом ( потенциальной стенкой ) называют силовое поле, в котором потенциальная энергия частицы имеет вид
Пусть слева на порог налетает частица с полной энергией Е . На языке квантовой теории это означает, что на порог слева «падает» дебройлевская волна
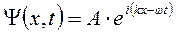
Чтобы удовлетворить граничным условиям для Ψ и 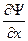
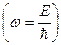
Задача состоит в том, чтобы сначала найти амплитуды отражённой и падающей волн, а затем коэффициенты отражения R и пропускания D .
Уравнение Шрёдингера для частицы в данном силовом поле имеет вид:
в области I( x 0 )
Общее решение уравнения Шрёдингера имеет вид:
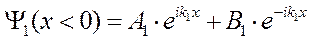
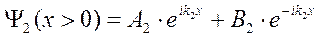
Будем считать, что падающая волна характеризуется амплитудой А1 , причём вещественной, а отражённая – амплитудой В1 . В области II( x > 0) имеется только проходящая волна, поэтому В2 = 0 .
Из условия непрерывности Ψ и 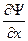
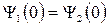
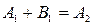
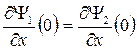
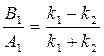
Для определения коэффициентов R и D вводят понятие плотности потока вероятности j , вектор которого определяется через волновую функцию следующим образом:
В соответствии с видом Ψ-функции для падающей, отражённой и прошедшей волн имеем:
Теперь можно записать
для коэффициента отражения
для коэффициента пропускания
Видно, что R + D = 1 , что и должно быть по определению. Коэффициенты R и D не зависят от направления движения частицы: слева направо или наоборот.
В классическом случае при E > U0 должно быть R = 0.
Эффектнадбарьерного отражения( R > O ) является чисто квантовым и объясняется наличием у частицы волновых свойств.
2). Высокий порог ( E
В этом случае 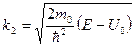
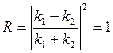
величины комплексно-сопряжённые. Таким образом, отражение будет полным, а D = 0.
Но волновая функция при x > 0 не обращается в нуль, т.е. микрочастицы могут проникать в области, которые для макроскопических частиц недоступны.
Плотность вероятности нахождения частицы в области II определяется выражением
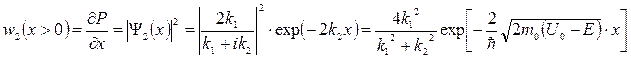
Для электрона с (U0 – E) = 1 эВ вероятность нахождения на расстоянии от порога сравнимым с размерами атома ( х = 10 -10 м ) достаточно велика, а на расстоянии в 10 раз большем ( х = 10 -9 м ) ничтожно мала.
Отражение хотя и является полным (R = 1) не обязательно происходит на самом пороге. Частица может проникнуть в область II , а затем выйти из неё ( аналогично полному внутреннему отражению в оптике).
Прохождение частицы через потенциальный барьер.
Рассмотрим одномерный прямоугольный потенциальный барьер
Частица движется слева направо. Слева от барьера имеем падающую и отраженную волну, а за барьером только прошедшую волну.
Уравнение Шрёдингера для областей I, II и III имеет вид:
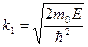
Волновые функции, являющиеся решением этих уравнений
Из решения этой системы уравнений получают, применив некоторые упрощающие допущения, выражение для коэффициента прозрачности D прямоугольного барьера
Для потенциального барьера произвольной формы
Пределы интегрирования х1 и х2 определяют из решения уравнения U( x ) = E .
Туннельный эффект
Прохождение частицы через потенциальный барьер, высота которого превышает энергию частицы, получило название туннельного эффекта (частица, проходя под барьером, как бы движется в туннеле). При прохождении через барьер полная энергия частицы Е не меняется.
Туннельный эффект представляет собой чисто квантовое явление.
Этим эффектом объясняются многие физические явления; например, холодная эмиссия электронов из металла (автоэмиссия), альфа-распад, спонтанное деление ядер и др.
На левом рисунке представлен потенциальный барьер треугольной формы, имеющий место на границе металл-вакуум в явлении холодной эмиссии электронов из металла. Электрон в металле находится в потенциальной яме глубиной U0 . Если вблизи поверхности металла имеется электрическое поле напряжённостью 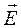
При туннелировании электронов через этот барьер происходит их выход из металла даже при низких температурах.
На правом рисунке представлен потенциальный барьер α-частицы в поле ядра. На больших расстояниях r между α-частицей и ядром действуют силы кулоновского отталкивания и потенциальная энергия частицы
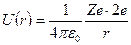
Ze – заряд дочернего ядра; 2е – заряд α-частицы.
Частица массой т0 падает на прямоугольный потенциальный барьер высотой U0 и шириной а . Энергия частицы Е больше высоты барьера.
В этом случае решение системы уравнений Шрёдингера для трёх областей: I – ( x a )даёт следующие значения для коэффициента прохождения D .

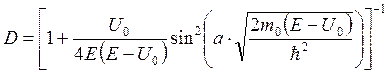
Частица беспрепятственно проходит над таким барьером ( D = 1) при значениях энергии равных
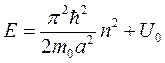
При других значениях энергии существует отличная от нуля вероятность отражения частицы от барьера.
Пролёт частицы над потенциальной ямойконечной глубины ( E > U0 )
Частица пролетает над потенциальной ямой конечной глубины U0 и ширины а слева направо вдоль оси ох.
Решая систему уравнений Шрёдингера для трёх областей, получаем выражение для коэффициента прохождения D , характеризующего вероятность прохождения частицы над ямой:
Коэффициент прохождения D зависит от соотношения между энергией частицы и глубиной потенциальной ямы и в общем случае оказывается меньше единицы (частица может отразится от потенциальной ямы даже если E > U0 ). Данное явление, полностью отсутствующее в классической физике, объясняется наличием у частицы волновых свойств.
Частица не испытывает отражения на границах ямы ( D = 1 ) только если sin = 0 . Это условие выполняется при значениях энергии частицы
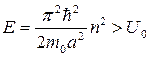
Рассмотренная модель поведения частицы вблизи симметричной прямоугольной потенциальной ямы конечной глубины хорошо качественно описывает движение электрона вблизи атома. В частности, проведённый анализ даёт квантово-механическое объяснение эффекта Рамзауэра, где наблюдалась аномальная прозрачность атомов инертных газов для пучка электронов при определённых значениях кинетической энергии (K = E – U0).
Условие 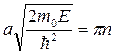
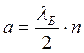
Видео:97. Микрочастица в потенциальной ямеСкачать

СТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
ОПИСАНИЕ ПОВЕДЕНИЯ ЭЛЕКТРОНА В КВАНТОВОЙ МЕХАНИКЕ
1. Уравнение Шредингера
Для выполнения лабораторных работ 6 и 7 необходимо знакомство с основами квантовой механики. Остановимся на тех её положениях, которые непосредственно связаны с содержанием данных работ.
В них изучается поведение микрочастицы (электрона) в определенных внешних условиях. Это означает, что потенциальная энергия электрона U, Обусловленная его взаимодействием с окружающими объектами, является известной функцией координат: 




Называемое Временны́м уравнением Шредингера, где I – мнимая единица, ( H – постоянная Планка), Ñ2 – оператор Лапласа (имеющий в декартовых координатах вид 


2. Уравнение Шредингера для стационарных состояний
Среди решений уравнения (Б.1) особый интерес представляют волновые функции вида

Описывающие состояния, называемые Стационарными. Легко проверить, что волновая функция вида (2) будет решением уравнения Шредингера (1), если 

Где 



Уравнение (3) называется Уравнением Шредингера для стационарных Состояний, или Стационарным уравнением Шредингера. Существенно, что стационарное уравнение Шредингера имеет физически приемлемые решения, вообще говоря, не для любых значений Е, А лишь для некоторого множества 


3. Волновая функция и заключенная в ней информация
Как уже говорилось, волновая функция описывает состояние частицы. Это означает, что в 

(звездочка обозначает комплексное сопряжение). Важную информацию о движении частицы дает выражающийся через 

Называемый вектором плотности потока вероятности. Он указывает направление наиболее быстрого перемещения вероятности и дает скорость этого перемещения. Смысл величин (4) и (5) раскрывается в эксперименте, когда производится N Измерений над электроном в одном и том же состоянии. Тогда при больших значениях N должно выполняться: DN¢ / N

J , где DN¢ – число электронов, обнаруженных в единичном объеме вблизи точки (Х, у, z), а DN¢¢ – результирующее число электронов, прошедших за единицу времени в направлении вектора 
В связи с приведенной интерпретацией выражений (4) и (5) волновую функцию 
Отметим, что для стационарных состояний выражения (4) и (5) не зависят от времени и что для вещественных 

4. Оптическая аналогия
Анализируя квантовомеханическую задачу, полезно сопоставлять ее, с одной стороны, с аналогичной задачей классической механики, а с другой – с некоторой оптической задачей. В классической механике аналогом, очевидно, будет задача о частице такой же массы, движущейся в силовом поле, характеризуемом той же потенциальной энергией , что и в исходной квантовой. Выяснив характер движения классической частицы, можно лучше понять особенности ее квантовомеханического поведения. Оптическим аналогом для квантовомеханической задачи с
E = Const будет, Как можно показать, задача о распространении монохроматической световой волны в неоднородной среде, для которой показатель преломления N Изменяется по закону

Отметим, что длину волны при этом можно оценивать по соотношению де Бройля 

Аналогия с оптикой позволяет во многих случаях, не решая уравнение Шредингера, предвидеть и объяснить качественно поведение y-функции, а следовательно и частицы.
5. Одномерные квантовомеханические задачи
Среди квантовомеханических задач выделяются своей простотой одномерные, т. е. такие, в которых U = U ( X ), а волновую функцию 

А стационарное уравнение Шредингера сводится к уравнению в обыкновенных производных

Уравнение (8) решается особенно просто, когда ось X можно разбить на области, в каждой из которых потенциал U(X) принимает постоянные значения, а на границах соседних областей испытывает скачок. Такой потенциал называется Прямоугольным Из-за прямых углов на его графике. Строго говоря, такие потенциалы не реализуемы, поскольку им соответствуют бесконечные силы в точках скачков потенциальной энергии. Все же прямоугольные потенциалы дают грубое представление о многих реальных системах, позволяя получать полезные результаты крайне простыми математическими методами.
В области, где потенциал U Постоянен, при E > U стационарное уравнение Шредингера (8) сводится к уравнению
Где 

Где А И В – произвольные постоянные.
При этом, в соответствии с (9) и (7), зависящая от времени
Волновая функция 

В котором первое слагаемое описывает волну, бегущую вправо, а второе – влево. При переходе от одной области к другой U изменяется и, следовательно, изменяется длина волны. Существенно, что на границе между областями, как уже отмечалось, y(Х) и ее первая производная D Y / D x должны быть непрерывны. Это приводит к двум уравнениям связи между амплитудными коэффициентами А и В для соседних областей.
6. Движение электрона в области потенциальной ступеньки
Рассмотрим случай, когда потенциал испытывает только один скачок (Потенциальная Ступенька, рис. 1). Предположим, что электроны с некоторой энергией Е Приходят слева. Согласно классической механике электроны должны беспрепятственно проходить точку Х = 0, поскольку в этой точке они испытывает действие силы, направленной в сторону своего движения (ускоряющей силы).
Используем, прежде всего, оптическую аналогию. Согласно (6) при X= 0 происходит скачкообразное изменение показателя преломления N , а при падении света на поверхность раздела двух сред с различными N часть волны отражается от неё, а часть проходит во вторую среду. Поэтому следует ожидать отражения в точке Х = 0 и для y-волны, а следовательно, отличной от нуля вероятности отражения электрона при падении на скачок потенциала как справа, так и слева.
Подтвердим эти предположения строгим расчетом на основе стационарного уравнения Шредингера (8). В области I, слева от скачка потенциала (т. е. при Х 0) для случая, когда электроны падают только слева, решение содержит лишь одно слагаемое, соответствующее прошедшей волне

Где 







Поскольку K2 > K1 , амплитуды отраженной и падающей волн имеют противоположные знаки. Это означает, что для падающей слева волны её фаза при отражении от скачка потенциала изменяется на π – происходит «потеря» полуволны.
Плотность потока электронов Г может быть выражена через их концентрацию Пе И скорость v : Г = Ne V. Поскольку Пе

K|ψ|2. Доля электронов, которые проходят вправо, т. е. коэффициент прохождения DЕ,, равен отношению плотности прошедшего потока к плотности падающего:

Аналогично рассчитывается и коэффициент отражения:

Те же выражения получаются в результате подсчета коэффициентов 



Вытекающим непосредственно из определения вектора плотности потока вероятности 
Легко проверить также, что 

Следует подчеркнуть, что свойство отражения частиц от скачков потенциала является чисто квантовомеханическим эффектом. Оно вытекает из волновых свойств материи и не имеет места в классической физике.
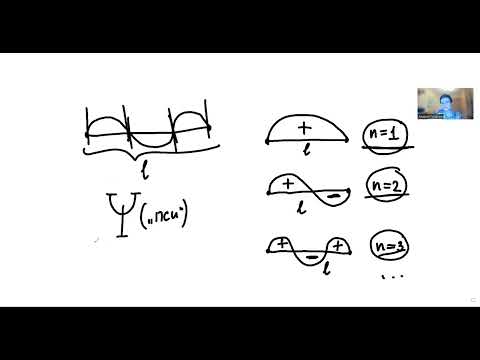
В заключение сформулируем квантовомеханическую задачу, позволяющую на примере одномерной прямоугольной симметричной потенциальной ямы (рис. 2) простыми методами рассмотреть квантование энергии электрона и дать качественное объяснение эффекта Рамзауэра.
В этой задаче потенциальная энергия электрона U (Х) задается в виде:


Величина L = 2 а – Ширина ямы, 
В зависимости от полной энергии электрона E, Возникают три случая:
📺 Видео
Туннельный эффектСкачать

QM_07 (Потенциальная ступенька)Скачать

Классические уравнения | уравнение Шрёдингера (координатное представление) | простейший выводСкачать

Лекция №4 "Волновая функция. Уравнение Шредингера" (Гавриков А.В.)Скачать

Уравнение ШрёдингераСкачать

Урок 32. Уравнение ШрёдингераСкачать
Урок 134. Применения уравнения Бернулли (ч.1)Скачать

Урок 456. Движение микрообъекта в одномерной бесконечно глубокой потенциальной ямеСкачать

Петров С.В. - Квантовая механика - 7. Особенности решения уравнения ШредингераСкачать

98. Туннельный эффектСкачать

2.1. Метод характеристик. Задача Коши для гиперболического уравнения на плоскости.Скачать

Лекция №4 " Потенциальные барьеры и ямы" (Глазков В.Н.)Скачать

QM_03 (Операторы импульса и энергии, уравнение Шредингера)Скачать

Лекция №04 "Уравнение Шредингера"Скачать

Лекции 5-6. Уравнение Шредингера и его приближенные решения. Межатомные.Скачать

Елютин П. В. - Квантовая теория I - Решение задач с помощью уравнения ШредингераСкачать

Урок 230. Простейшие задачи на электрический потенциалСкачать