Решение уравнения шредингера для атома водорода в квантовой механике

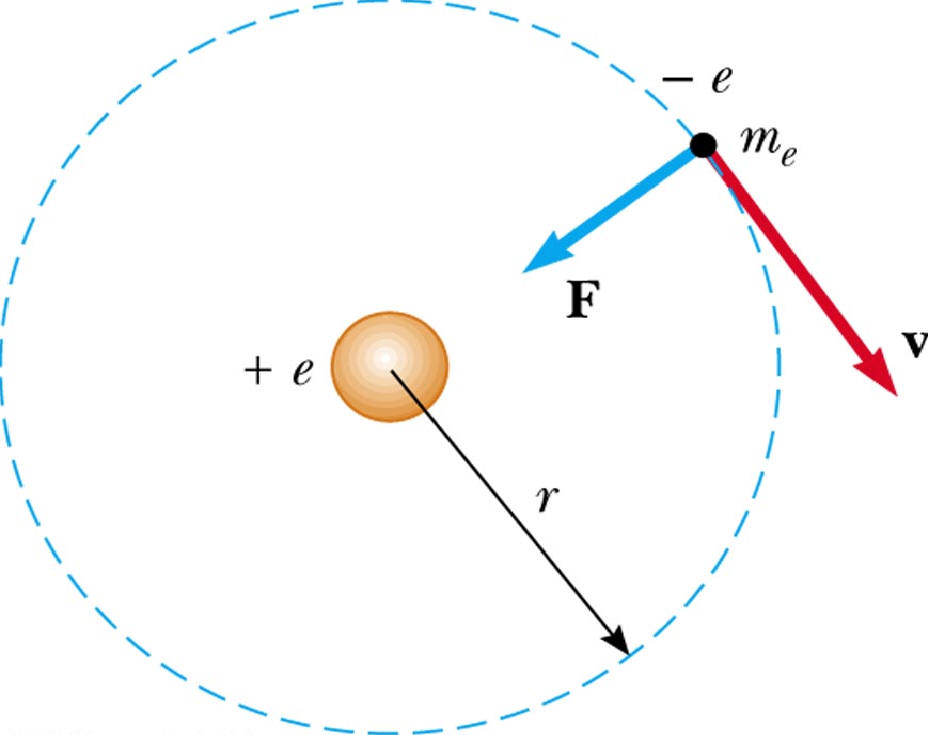
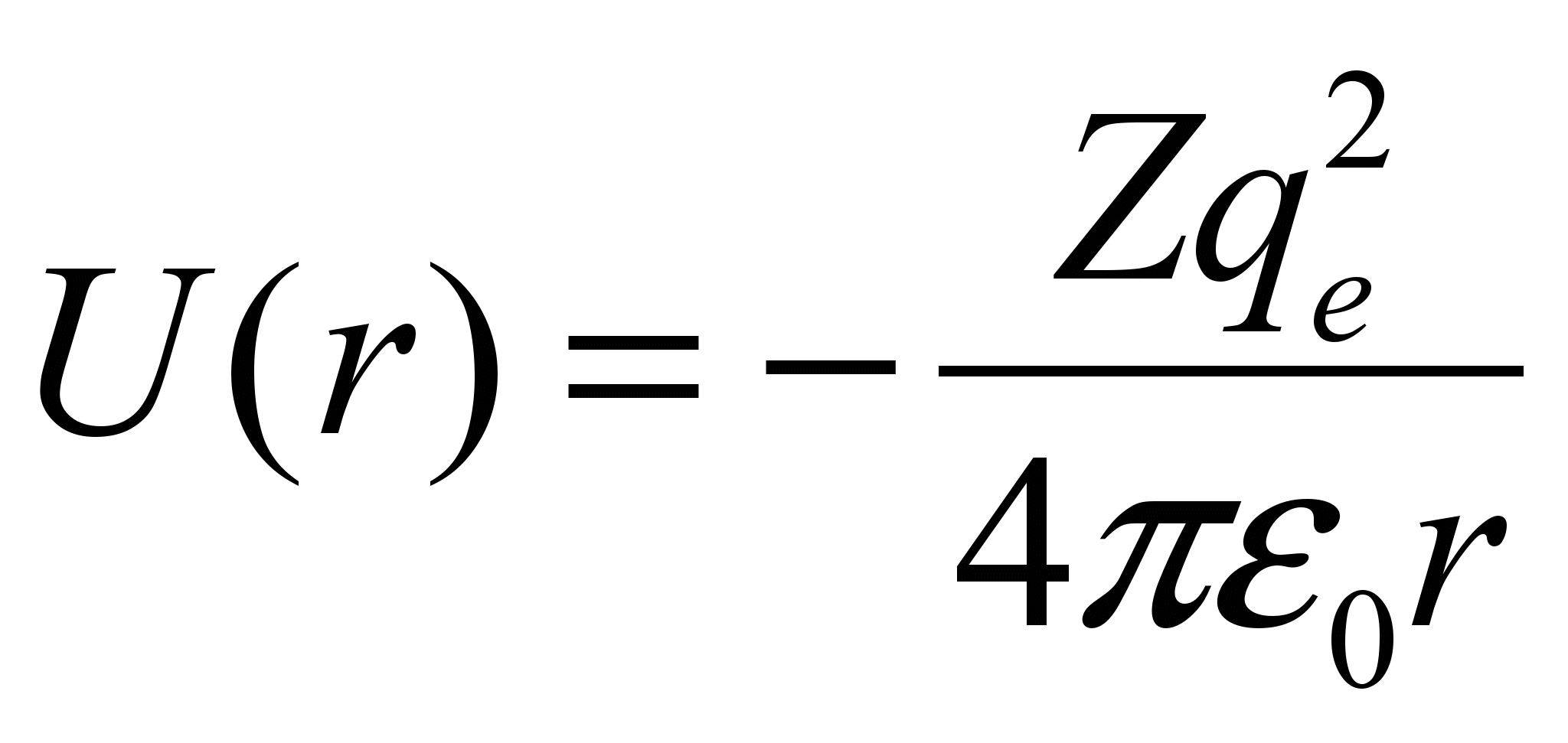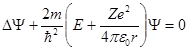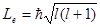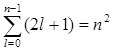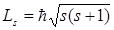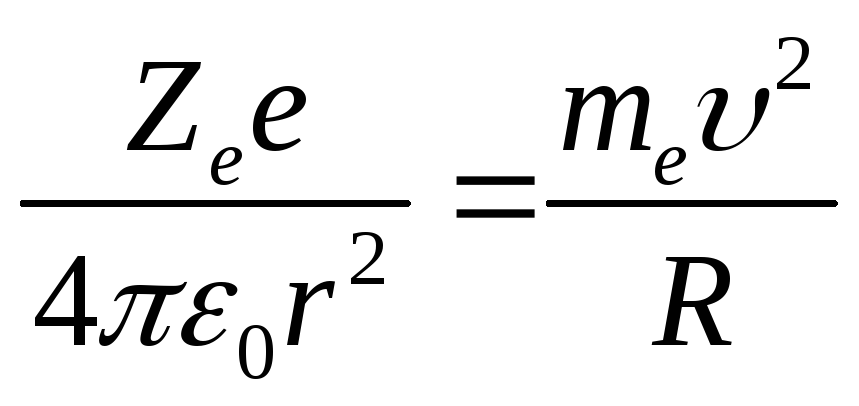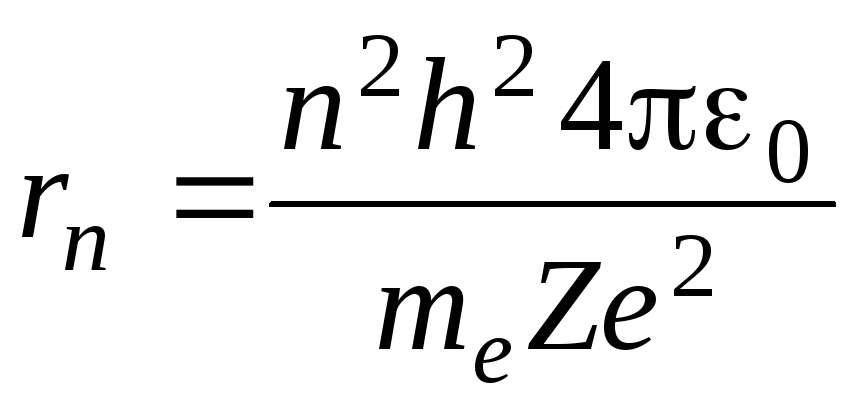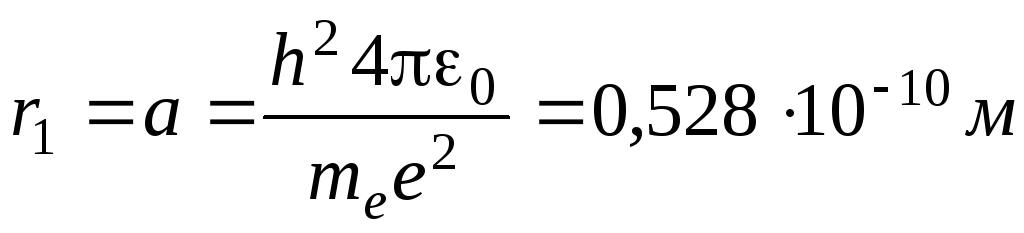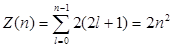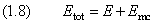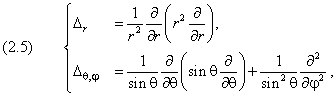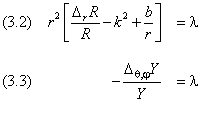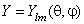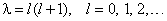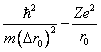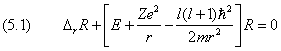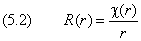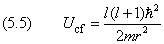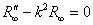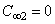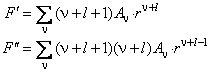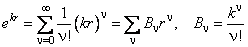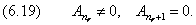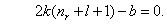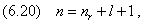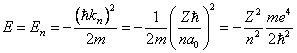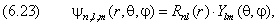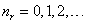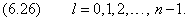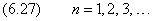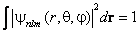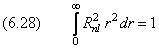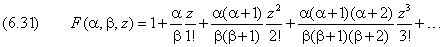Атом водорода и водородоподобные системы – это системы, состоящие из ядра с зарядом Ze и одного электрона (например, ионы He + , Li 2+ ).

Решение задачи об энергетических уровнях электрона для атома водорода (а также водородоподобных систем: иона гелия Не + , двукратно ионизованного лития Li + + и др.) сводится к задаче о движении электрона в кулоновском поле ядра.

Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Zе (для атома водорода Z =1):

Состояние электрона в атоме водорода описывается волновой функцией Ψ, удовлетворяющей стационарному уравнению Шредингера

Его решения позволяют определить характеристики ВДПА:

Энергия . В теории дифференциальных уравнений доказывается, что такие уравнения имеют решения, удовлетворяющие требованиям однозначности, конечности и непрерывности волновой функции Ψ, только при собственных значениях энергии

при n = 1, 2, 3.

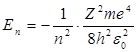
т. е. для дискретного набора отрицательных значений энергии.

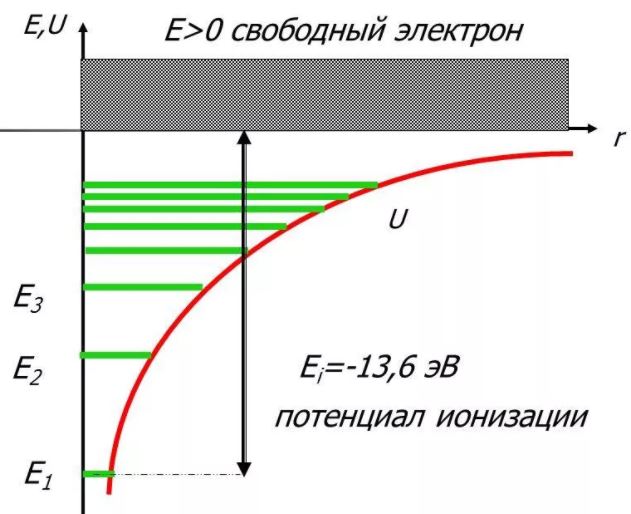
Таким образом, как и в случае «потенциальной ямы» с бесконечно высокими «стенками», решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней. Самый нижний уровень Е₁, отвечающий минимальной возможной энергии, – основной, все остальные (Е_n>E₁, n = 2, 3,…) – возбужденные. При Е 0 движение электрона является свободным; область непрерывного спектра Е >0 соответствует ионизованному атому.

Энергия ионизации атома водорода равна

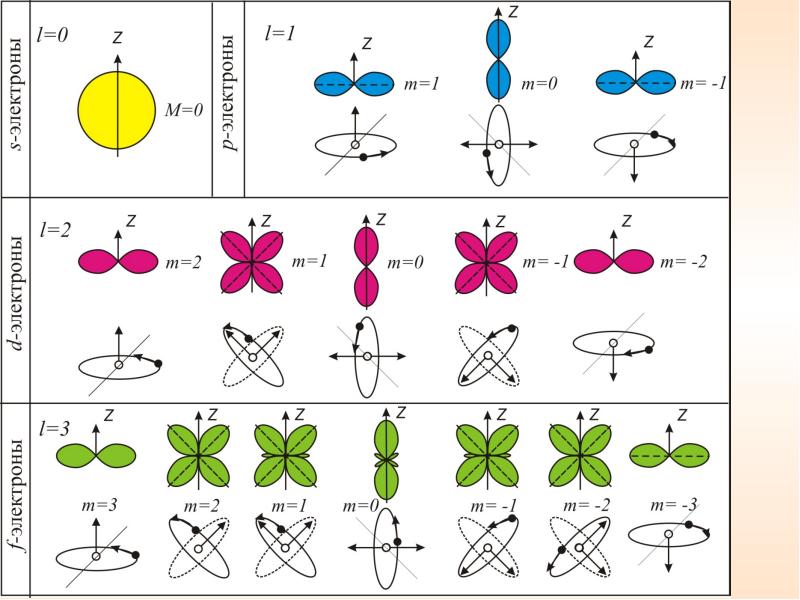
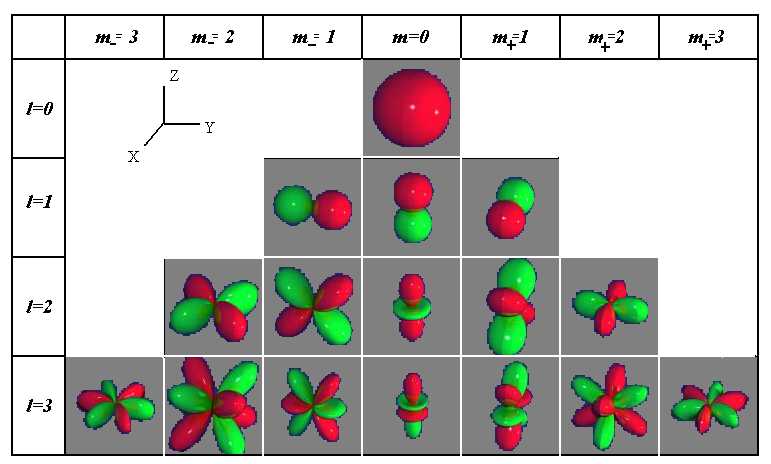
Квантовые числа . В квантовой механике доказывается, что уравнению Шредингера удовлетворяют собственные функции Ψ, определяемые тремя квантовыми числами: главным п, орбитальным l и магнитным m_l.

Главное квантовое число n, определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения, начиная с единицы:

Из решения уравнения Шредингера вытекает, что момент импульса (механический и орбитальный момент) электрона квантуется, т. е. не может быть произвольным, а принимает дискретные значения, определяемые формулой

где l – орбитальное квантовое число,которое при заданном n принимает значения

т. е. всего п значений, и определяет момент импульса электрона в атоме.

Из решения уравнений Шредингера следует также, что вектор L_e момента импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция L_еz а направление z внешнего магнитного поля принимает квантованные значения, кратные ħ

где т_l – магнитное квантовое число,которое при заданном l может принимать значения

т.е. всего 2l+1 значений. Таким образом, магнитное квантовое число т_l определяет проекцию момента импульса электрона на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2l + 1 ориентаций.

Так как при данном п орбитальное квантовое число l может изменяться от 0 до n – 1, а каждому значению l соответствует 2l + 1 различных значений т_l, то число различных состояний, соответствующих данному n, равно

Опыт Штерна и Герлаха

О. Штерном и В. Герлахом были поставлены опыты (1921), целью которых являлось измерение магнитных моментов р _m атомов различных химических элементов. Для определения орбитального момента импульса L _l и р _m одного электрона опыты должны быть поставлены с атомами, у которых орбитальные механические (и магнитные) моменты всех электронов, кроме одного, взаимно компенсируют друг друга. Такими атомами являются атомы химических элементов, образующие первую группу периодической системы Менделеева и имеющие один валентный электрон на внешней оболочке.

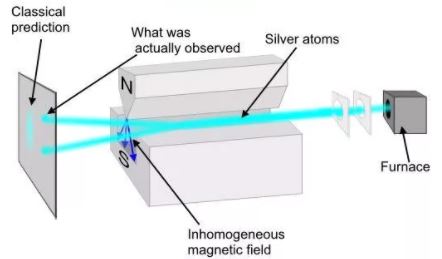
Идея опытов Штерна и Герлаха заключалась в измерении силы, действующей на атом в неоднородном магнитном поле. Опыты Штерна и Герлаха обнаружили ошибочность классического предположения отом, что магнитный момент р_m и механический момент импульса L_l атома произвольно ориентируются относительно направления внешнего поля, и подтвердили наличие пространcтвенного квантования.

В трубке, где был создан вакуум порядка 10 -5 мм рт. ст., помещался источник пучка атомов — нагреваемый до высокой температуры серебряный шарик К. Атомы серебра вылетали с его поверхности со средней тепловой скоростью порядка 100 м/с, соответствующей температуре испарения серебра. Из этих атомов при помощи щелевых диафрагм В вырезался узкий пучок, проходящий через сильное и неоднородное магнитное поле, направленное перпендикулярно пучку. Основная трудность опыта состояла в том, чтобы достигнуть такой большой неоднородности магнитного поля, которая сказывалась бы на расстояниях порядка размеров атома. При такой величине неоднородности поля можно было рассчитывать получить значительную отклоняющую силу F, действующую на атом в магнитном поле. Необходимая неоднородность поля была достигнута в результате применения сильного электромагнита SN с полюсными наконечниками специальной формы. Приемником атомов серебра служила фотопластинка А.

Если бы момент импульса L_l атома (и его магнитный момент р_m ) мог принимать произвольные ориентации в магнитном поле, то можно было бы ожидать непрерывного распределения попаданий атомов на пластинку с большей плотностью попаданий в середине пластинки и меньшей плотностью к ее краям. Опыты, проведенные с серебром и атомами других элементов периодической системы, привели к совершенно другому результату. На рисунке показана фотография результата опыта Штерна и Герлаха с литием. Из рисунка видно, что на фотопластинке получились две резкие полосы — все атомы отклонялись в магнитном поле двояко, что соответствовало лишь двум возможным ориентациям магнитного момента во внешнем поле. Момент импульса атома (и его магнитный момент) равен суммарным моментам электронов, поскольку магнитные моменты ядер имеют значительно меньшее значение, чем магнитные моменты электронов. Последние совпадают с суммарными моментами валентных электронов, так как моменты электронов замкнутых оболочек компенсируются.

Для объяснения этого американские физики Д. Уленбек (1900- 1974) и С. Гаудсмит (1902-1979) предположили, что электрон обладает собственным неуничтожимым механическим моментом импульса, не связанным с движением электрона в пространстве — спином.

Спин электрона (и всех других микрочастиц) — квантовая величина, у нее нет классического аналога; это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.

Если электрону приписывается собственный механический момент импульса (спин) L_s, то ему соответствует собственный (спиновый) магнитный момент р_ms,. Согласно общим выводам квантовой механики, спин квантуется по закону

где s – спиновое квантовое число.

По аналогии с орбитальным моментом импульса, проекция L_sz, спина квантуется так, что вектор L_s, может принимать 2s + 1 ориентаций. Так как в опытах Штерна и Герлаха наблюдались только две ориентации, то 2s + 1 = 2, откуда s = 1 / 2. Проекция спина на направление внешнего магнитного поля, являясь квантованной величиной, определяется выражением

где m_s – магнитное спиновое квантовое число; оно может иметь только два значения: m_s = ± ½.

Таким образом, опытные данные привели к необходимости характеризовать электроны (и микрочастицы вообще) добавочной внутренней степенью свободы. Поэтому для полного описания состоянии электрона в атоме необходимо наряду с главным, орбитальным и магнитным квантовыми числами задавать еще магнитное спиновое квантовое число.

Движение электрона в атоме водорода по круговой орбите радиусом r описывается уравнением:

Найдем радиус n-орбиты:

Для атома водорода радиус первой орбиты электрона (первый боровский радиус) равен

Принцип запрета Паули

Если перейти от рассмотрения движения одной микрочастицы (одного электрона) к многоэлектронным системам, то проявляются особые свойства, не имеющие аналога в классической физике. Пусть квантово-механическая система состоит из одинаковых частиц, например электронов. Все электроны имеют одинаковые физические свойства – массу, электрический заряд, спин и др. внутренние характеристики (например, квантовые числа). Такие частицы называют тождественными, которые невозможно экспериментально различить тождественные частицы.

В классической механике даже одинаковые частицы можно различить но положению в пространстве и импульсам. Если частицы в какой-то момент времени пронумеровать, то в следующие моменты времени можно проследить за траекторией любой из них. Классические частицы, таким образом, обладают индивидуальностью.

В квантовой механике положение иное. Из соотношения неопределенностей вытекает, что для микрочастиц вообще неприменимо понятие траектории; состояние микрочастицы описывается волновой функцией, позволяющей вычислять лишь вероятность (|Ψ| 2 ) нахождения микрочастицы в окрестностях той или иной точки пространства. Если же волновые функции двух тождественных частиц в пространстве перекрываются, то разговор о том, какая частица находится в данной области, лишен смысла: можно лишь говорить о вероятности нахождения в данной области одной из тождественных частиц. Таким образом, в квантовой механике тождественные частицы полностью теряют свою индивидуальность и становятся неразличимыми.

Принцип неразличимости тождественных частиц ведет к определенному свойству симметрии волновой функции. Если при перемене частиц местами волновая функция не меняет знака, то она называется симметричной,если меняет антисимметричной.Изменение знака волновой функции не означает изменения состояния, так как физический смысл имеет лишь квадрат модуля волновой функции. В квантовой механике доказывается, что характер симметрии волновой функции не меняется со временем.

Установлено, что симметрия или антисимметрия волновых функций определяется спином частиц. В зависимости от характера симметрии все элементарные частицы и построенные из них системы (атомы, молекулы) делятся на два класса.

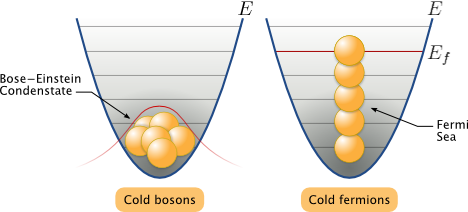
Частицы с полуцелым спином (например, электроны, протоны, нейтроны) описываются антисимметричными волновыми функциями и подчиняются статистике Ферми – Дирака; эти частицы называются фермионами.

Частицы с нулевым или целочисленным спином (например, π-мезоны, фотоны) описываются симметричными волновыми функциями и подчиняются статистике Бозе – Эйнштейна; эти частицы называются бозонами.

Сложные частицы (например, атомные ядра), составленные из нечетного числа фермионов, являются фермионами (суммарный спин – полуцелый), а из четного бозонами (суммарный спин целый).

Зависимость характера симметрии волновых функций системы тождественных частиц от спина частиц теоретически обоснована швейцарским физиком В. Паули (1900—1958), что явилось еще одним доказательством того, что спин является фундаментальной характеристикой микрочастиц.

Квантово-механическая формулировка принципа Паули:

Два одинаковых фермиона, входящих в одну систему, не могут находиться в одинаковых состояниях, так как для фермионов волновая функция должна быть антисимметричной.

Отметим, что число однотипных бозонов, находящихся в одном и том же состоянии, не лимитируется.

Таким образом, принцип Паули утверждает, что два электрона, связанные в одном и том же атоме, различаются значениями по крайней мере одного квантового числа.

Согласно принципу, данному п соответствует п 2 различных состояний электронов, отличающихся значениями l и т_l. Квантовое число m_s, может принимать лишь два значения (±1/2). Поэтому максимальное число электронов, находящихся в состояниях, определяемых данным главным квантовым числом, равно

Совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число n, называют электронной оболочкой.

В каждой из оболочек электроны распределяются по подоболочкам, соответствующим данному l. Поскольку орбитальное квантовое число принимает значения от 0 до п – 1, число подоболочек равно порядковому номеру п оболочки. Количество электронов в подоболочке определяется магнитным и магнитным спиновым квантовыми числами: максимальное число электронов в под оболочке с данным l равно 2 (2l+ 1).

Многоэлектронный атом

В многоэлектронном атоме, заряд которого равен Ze, электроны будут занимать различные «орбиты» (оболочки). При движении вокруг ядра Z‑электроны располагаются в соответствии с квантово‑механическим законом, который называется принципом Паули (1925 г.). Он формулируется так:

1. В любом атоме не может быть двух одинаковых электронов, определяемых набором четырех квантовых чисел: главного n, орбитального /, магнитногоm и магнитного спиновогоm_s.

2. В состояниях с определенным значением могут находиться в атоме не более 2n 2 электронов.

Значит, на первой оболочке («орбите») могут находиться только 2 электрона, на второй – 8, на третьей – 18 и т. д.

Таким образом, совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число n, называют электронной оболочкой . В каждой из оболочек электроны располагаются по подоболочкам, которые соответствуют определенному значению /. Так как орбитальное квантовое число l принимает значения от 0 до (n – 1), число подоболочек равно порядковому номеру оболочки п. Количество электронов в подоболочке определяется магнитным квантовым числом m_l и магнитным спиновым числом m_s.

Видео:Урок 455. Уравнение ШрёдингераСкачать

Решение уравнения шредингера для атома водорода в квантовой механике

В этой главе излагается решение уравнения Шредингера в рамках задачи Кеплера. Мы убедимся, что без учёта релятивистских эффектов положение энергетических уровней получается таким же, как и в теории Бора–Зоммерфельда, но определяемая волновой функцией форма орбиталей в квантовой теории отличается от классических траекторий. В случае кулоновского поля существуют аналитические выражения для волновых функций, что позволяет вычислить средние значения физических параметров и, например, получить представление о размерах атома в различных состояниях.

Анализ задачи с позиций квантовой механики позволяет выяснить природу основного состояния любого атома, понять причину сгущения уровней вблизи границы ионизации, а также дать ответ на вопрос о вырождении энергетических уровней. Квантовые числа углового момента, которые определяют структуру волновой функции, необходимы при классификации спектров сложных атомов, для которых аналитическое решение уравнения Шредингера невозможно.

Проблема атома водорода и, в особенности, водородоподобных ионов с большим зарядом ядра, требует учёта релятивистских эффектов. Один из них — зависимость массы электрона от скорости — в главе 13 рассмотрен в классическом приближении. Мы увидели, что при переходе к тяжёлым атомам этот эффект растёт быстро, пропорционально Z 4 , но, тем не менее, остаётся малым вплоть до элементов группы железа. Аналогичными свойствами обладает спин–орбитальное взаимодействие. Его роль заключается в снятии вырождения уровней, характерного для нерелятивистской модели атома. Задача о кулоновском поле имеет аналитическое решение и в релятивистском случае. Но для атомов вплоть до элементов группы железа оба упомянутых эффекта малы по сравнению с электростатическим взаимодействием и могут быть рассмотрены как малые поправки к полученным в этой главе формулам.

Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

16.1 Приведённая масса

Рассмотрим взаимодействие двух заряженных частиц по закону Кулона. С потенциальной энергией (13.3.3) стационарное уравнение Шредингера для волновой функции системы ψ_SYS имеет вид

.

Здесь r_e и r_Z —радиус–векторы, соответственно, электрона и ядра, E_tot — полная энергия системы. Введём положение центра инерции частиц

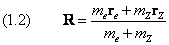
и электрона относительно ядра

.

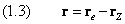
Две последние формулы соответствуют определениям (13.2.3) и (13.2.4) классической механики. Выполним замену переменных в операторах дифференцирования в левой части (1.1):

Подставив (1.4) в (1.1), приходим к уравнению

.

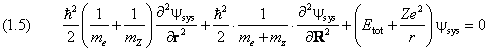
Оно допускает разделение переменных. Представим волновую функцию в виде произведения

,

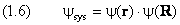
где первый множитель не зависит от R, а второй — от r. Разделим (1.5) на ψ_SYS и второе слагаемое слева перенесём в правую часть:

.

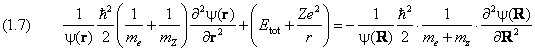
Левая и правая части последнего уравнения зависят от разных переменных, поэтому каждая из них должна быть равна константе. Полная энергия E_tot системы складывается из её внутренней энергии E и энергии E_mc движения центра масс электрона и ядра:

,

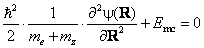
описывает равномерное прямолинейное движение центра масс, а уравнение

есть искомое уравнение Шредингера для относительного движения. Как и в классической механике, задача сводится к движению вокруг ядра частицы, занимающей место электрона, но масса её равна приведённой массе системы (13.2.6).

Видео:Урок 459. Обзор квантовой теории атома водородаСкачать

16.2. Новые параметры

В связанном состоянии энергия частицы E, как известно, отрицательна. Вместо неё будем пользоваться «дебройлевским» волновым числом:

.

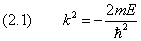
Введём масштаб длины
.

Напомним, что a₀ — боровский радиус (1.2.7). В этих обозначениях уравнение (1.9) приобретает следующий вид:

.

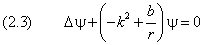
Удобно перейти к сферическим координатам, в которых оператор Лапласа равен сумме

,

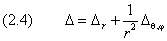
называются, соответственно, «радиальным» и «угловым» лапласианом. Напомним, что угловой лапласиан, согласно (12.5.1), с точностью до знака равен оператору квадрата момента количества движения l 2 . Перейдём к решению задачи.

Видео:Квантовые числа (видео 14) | Квантовая физика | ФизикаСкачать

16.3. Разделение сферических переменных

Покажем, что в сферических координатах задача допускает дальнейшее разделение переменных. Волновую функцию ищем в виде произведения

.

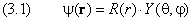
Подставим (3.1) в (2.3), разделим полученное уравнение на ψ(r) и перенесём в правую часть слагаемое с оператором, действующим на угловые переменные:

.

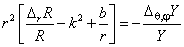
Слева и справа от знака равенства стоят функции от разных аргументов. Следовательно, обе они равны одной и той же константе:

Уравнение (3.3) совпадает с (12.5.3) и, таким образом, представляет собой задачу на собственные значения квадрата момента. Согласно (12.5.5) и (12.6.2), она имеет ограниченное и однозначное решение

Подставляя это значение λ в (3.2), получим обыкновенное дифференциальное уравнение для радиальной части волновой функции:

.

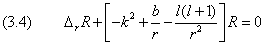
Прежде, чем приступить к его решению, проведём качественные исследования некоторых свойств радиального движения.

Видео:ЧК МИФ 5 2 01 01 L4 Уравнение Шредингера для атома водородаСкачать

16.4. Свойства движения в кулоновском поле

Наличие основного состояния и сгущение уровней вблизи границы ионизации — оба этих свойства кулоновского поля являются следствием соотношения неопределённостей.

Рассмотрим волновую функцию электрона, локализованного внутри малой сферы радиуса r₀. Неопределённость в значениях его координат приблизительно равна r₀, неопределённость в значении импульса, соответственно, порядка ħ/r ₀ , а среднее значение кинетической энергии T составляет ħ 2 /mr ₀ 2 . Полная энергия, равная сумме
,

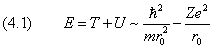
не может неограниченно убывать по мере уменьшения r₀. Следовательно, дискретный спектр начинается с некоторого отрицательного конечного значения. Иными словами, в кулоновском поле имеется основное состояние.

Этот результат отличается от движения в потенциальной яме бесконечной глубины, где отрицательная энергия дискретных уровней неограниченно растёт по абсолютной величине. Различие обусловлено степенью крутизны потенциальной функции. Если в (4.1) вместо кулоновского потенциала подставить, например

с достаточно большим показателем степени:

то энергия E при уменьшении r₀ становится отрицательной, неограниченно увеличиваясь по абсолютной величине. Но если средняя энергия может принимать такие значения, то это означает, что существуют сколь угодно глубокие уровни. Потенциальная яма имеет стенки, более крутые, чем любаястепеннáя функция, следовательно, её уровни энергии действительно не должны иметь нижней границы.

Ещё раз обратим внимание на то, что существование основного состояния атома является чисто квантовым явлением. В классической механике при равном нулю моменте обязательно имеет место падение электрона на ядро.

Теперь исследуем характер энергетического спектра электрона, находящегося на больших расстояниях от ядра. Рассмотрим волновой пакет, «заполняющий» шаровой слой большого радиуса r₀ и толщины Δr r₀. Тогда порядок величины кинетической энергии будет ħ 2 / m( Δr ) 2 . Теперь увеличиваем r ₀ и, пропорционально ему, Δr ₀ . Для электрона в кулоновском потенциале при достаточно больших значениях r ₀ сумма

(4.2)

станет отрицательной. Таким образом, существуют стационарные состояния с отрицательной энергией, в которых частица может находиться на больших расстояниях от ядра. Но это означает, что существуют сколь угодно малые по абсолютной величине уровни энергии. Иными словами, дискретный спектр содержит бесконечно много уровней, сгущающихся к границе ионизации. Снова мы видим кардинальное отличие от решения задачи о потенциальной яме. Причина та же: большая крутизна потенциальной функции. Из (4.2) легко убедиться, что в случае α>2 никакого сгущения уровней ожидать не приходится.

По сути дела, мы убедились, что у каждой атомной системы есть основное состояние с конечным значением энергии, и её уровни сгущаются по мере приближения к границе ионизации. Оба эти заключения следуют из того, что потенциальная функция любого иона и атома близка к закону Кулона как вблизи ядра, так и на очень больших расстояниях от него. Вблизи ядра можно пренебречь влиянием электронов, и потенциальную энергию (отрицательную) описывает формула Ze 2 / r. Вдали от него справедлива изложенная в разделе 13.8 модель атомного остатка. Потенциальная энергия оптического электрона в этой модели также описывается законом Кулона и пропорциональна отношению (Z–N+1)e 2 / r, где N — число электронов в ионе или атоме.

Видео:Квантовая физика. Лекция-семинар 8. Решение уравнения Шредингера для атома водорода.Скачать

16.5. Эффективный потенциал

Покажем, что решение радиальной части (3.4) волнового уравнения не имеет вырождения. На время вернёмся к обозначениям первого раздела. Вынесем за скобки множитель 2m / ħ 2 и с учётом (2.1) и (2.2) получим:

(5.1) приводится к виду

.

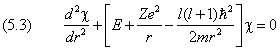
Последнее уравнение описывает одномерное движение в поле с потенциальной энергией

.

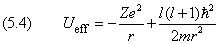
На первом месте здесь стоит потенциальная энергия электрона. Числитель второго слагаемого равен собственному значению квадрата момента. В связи с этим величину

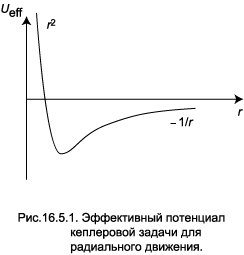
в квантовой теории, как и в классической механике, принято называть «центробежным потенциалом», а сумму (5.4) — «эффективным потенциалом». Профиль эффективного потенциала схематически изображён на рис.16.5.1.

На больших расстояниях от ядра превалирует кулоновский потенциал, а на малых — центробежный. Поэтому эффективный потенциал имеет минимум. Его зависимость от r напоминает яму конечной глубины, но в отличие от ямы здесь пологие края.

Уравнение (5.3) показывает, что задача о радиальном движении в кулоновском поле сводится к задаче об одномерном движении в области, ограниченной с одной стороны. Как показано во втором разделе девятой главы, ограниченное одномерное движение является невырожденным. Отсюда следует заключение об отсутствии вырождения по радиальной координате и в случае кулоновского поля. Таким образом, вырождение волновой функции кулоновского поля обусловлено исключительно её угловой частью.

Перейдём к определению энергетических уровней, поставив условие ограниченности волновой функции.

Видео:Хренова М.Г. - Квантовая химия - 2. Атом водородаСкачать

16.6. Вычисление радиальной части волновой функции

Раскроем радиальную часть лапласиана Δ_r:

.

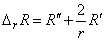
Подставив полученное выражение в (3.4), приходим к уравнению

.

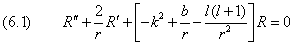
Его, как и уравнение, описывающее линейный осциллятор, решаем методом разложения в ряд с предварительным выделением особых точек.

Особые точки

В рассматриваемой здесь задаче присутствуют две особые точки: бесконечно удалённая точка r→∞ и начало координат r=0 . Введём обозначения R_∞ для волновой функции на больших расстояниях от ядра и R₀ — вблизи него. Для выяснения зависимости R_∞(r) опустим в (6.1) все слагаемые, содержащие в знаменателе r. Получающееся в результате уравнение

.

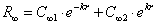
Из условия ограниченности волновой функции вытекает требование

и окончательно приходим к результату

.

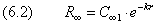
Поведение волновой функции вблизи ядра определяется как раз теми слагаемыми, которые мы опустили при поиске R_∞. Предположим, что орбитальный момент отличен от нуля: l>0 . Тогда в квадратных скобках (6.1) можно пренебречь первым и вторым членами по сравнению с центробежным потенциалом:

.

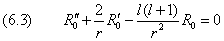
Решение последнего уравнения ищем в виде степеннóй функции

,

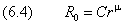
для которой надо найти значение показателя степени μ. После подстановки (6.4) в (6.3) приходим к квадратному уравнению для μ:

,

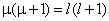
два корня которого равны:

.

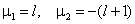
Таким образом, решением уравнения (6.3) является линейная комбинация

.

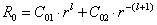
Из требования ограниченности волновой функции следует

.

.

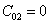
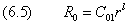
В случае l=0 уравнение (6.3) имеет решение

что формально не противоречит (6.5).

Итак, формулы (6.2) и (6.5) описывают поведение волновой функции, соответственно, в бесконечно удалённой точке и вблизи начала координат.

Разложение в ряд

Решение для произвольного диапазона радиальной координаты будем искать в виде

,

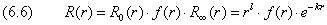
причём константы C ₀₁ и C_{∞ 1} из (6.5) и (6.2) включены в искомую функцию f(r). Её мы представляем в виде ряда

.

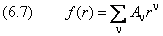
Запишем выражение для радиальной функции:

.

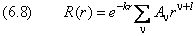
Исключим из исходного уравнения (6.1) слагаемое с первой производной. Для этого выполним замену переменной:

.

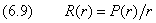
Функция P(r) может быть разложена в ряд аналогично (6.8):

Оператор Лапласа, применённый к функции P(r), содержит только вторую производную:

.

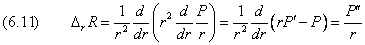
Теперь перепишем уравнение (6.1) в виде:

.

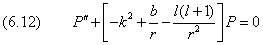
Подставим в него P(r) из (6.10a) и получим уравнение для функции F(r):

.

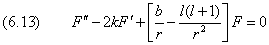
Дважды дифференцируя ряд (6.10b): (6.10),

и подставляя его в (6.13), получим бесконечную систему уравнений для коэффициентов разложения:

Увеличим на единицу индекс суммирования в первом и последнем членах суммы, после чего вынесем за скобки общий множитель r ν+l :

.

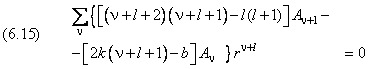
Поскольку последнее равенство выполняется при произвольных значениях переменной r, коэффициенты при всех степенях r ν+l должны быть равны нулю. Отсюда следует рекуррентное соотношение:

.

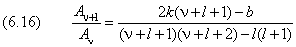
Задав значение A ₀ , мы можем вычислить коэффициент разложения с любым номером.

Только конечная сумма даёт ограниченное решение

Покажем, что, как и в случае линейного осциллятора (глава 11), условию ограниченности волновой функции R(r)удовлетворяет только конечная сумма, но не бесконечный ряд. Для этого достаточно убедиться, что такой ряд растёт быстрее, чем e kr . В самом деле, при неограниченном возрастании номера ν отношение коэффициентов ряда (6.16) стремится к пределу

.

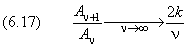
А в разложении экспоненты:

отношение коэффициентов равно

.

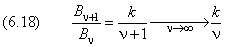
Сравнение (6.17) и (6.18) показывает, что в случае бесконечного ряда волновая функция R(r) не стремится к нулю при неограниченном удалении от ядра. Физический смысл имеет только решение уравнения (6.13) в виде конечной суммы.

Условие квантования энергии

В конечной сумме существует номер ν=n_r такой, что

Параметр n_r называется радиальным квантовым числом. Он аналогичен введённой в предыдущей главе величине n_r и, как мы увидим ниже, принимает тот же ряд значений (15.1.23). Согласно (6.16) и (6.19), решение существует только в том случае, если k удовлетворяет условию

Таким образом, волновое число электрона квантуется: оно определяется линейной комбинацией

называемой главным квантовым числом. Снова прослеживается аналогия с классической моделью атома: (6.20) получается из (15.1.11) заменой n_φ на l+1. Эта замена обусловлена принципиально разной интерпретацией состояний с равным нулю моментом в квантовой теории и классической механике. Выпишем в явной форме правило квантования волнового числа:

.

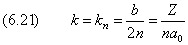
Из соотношений (2.1) и (6.21) получим условие квантования энергии:

или, вспоминая определение ридберга (13.5.3):

Эта формула даёт собственные значения нашей задачи. Собственные функции (волновые функции) зависят от трёх координат (r, θ, φ) и трёх параметров (n, l, m):

где Y_lm — угловая часть волновой функции, R_nl — радиальный множитель, равный

.

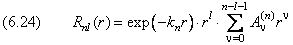
Коэффициенты суммы связаны друг с другом рекурренным соотношением

.

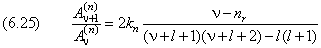
Сумма в (6.24) является знакопеременной. В этом легко убедиться, заметив, что числитель дроби (6.25) имеет отрицательный знак.

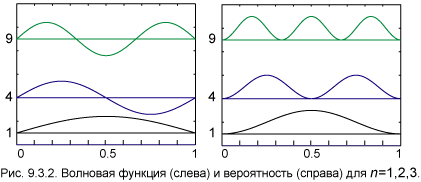
К радиальной волновой функции применима осцилляционная теорема, о которой шла речь в разделе 9.3. Число узлов функции R_nl равно квантовому числу n_r.

Уточним диапазон изменения квантовых чисел n, n_r и l. Согласно (12.1), параметр l должен быть неотрицательным. Нумерация слагаемых под знаком суммы в (6.24) начинается с нуля, поэтому n_r принимает целые значения:

Энергетический уровень однозначно определяется главным квантовым числом n. Из (6.20) следует, что при заданном значении n орбитальное квантовое число может быть равно одному из чисел ряда:

Если в (6.20) равны нулю оба параметра: 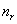и l , — то n равно единице. Остальным парам чисел соответствуют б óльшие значения n . Итак:

Обратим внимание на то, что орбитальное квантовое число выпало из окончательного результата (6.22), хотя в уравнении Шредингера (6.1) оно присутствует. Этот факт является следствием особо высокой степени симметрии кулоновского поля — более высокой, чем просто поле с центральной симметрией. В общем случае центрально-симметричного поля, потенциал которого падает по закону, отличному от 1/r, энергия зависит от квантового числаl.

Нормированная волновая функция

Разложение (6.23) волновой функции на множители, каждый из которых зависит либо от радиальной, либо от угловых координат, позволяет разбить общее условие нормировки

на два: по радиальной координате

.

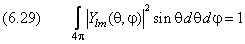
Для справочных целей выпишем полные выражения для нормированных волновых функций. Сумма в (6.24) с рекуррентным соотношением (6.25) для коэффициентов может быть выражена через так называемую гипергеометрическую функцию. Радиальная часть волновой функции с учётом условия нормировки равна

Здесь F — вырожденная (конфлюэнтная) гипергеометрическая функция (функция Куммера):

которая сходится при всех конечных z ; параметр α произволен, а β предполагается не равным нулю или целому отрицательному числу. Если α есть целое отрицательное число (или нуль), то F( α , β , z ) сводится к полиному степени | α |. Радиальные волновые функции выражаются также через обобщённые полиномы Лагерра :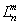

Угловая часть волновой функции описана в разделе (12.6).

В литературе можно увидеть различные формулы для волновой функции в кулоновском поле. Они отличаются друг от друга комплексной константой, квадрат модуля которой равен единице. Это различие не является существенным, так как в любом физическом эксперименте измеряется вероятность обнаружения частицы, равная именно квадрату модуля волновой функции.

Заметим, что размерность волновой функции равна см –d/2 , где d — размерность задачи. В нашем случае размерным множителем в (6.30) является комбинация ( 2k_n ) 3/2 . Остальные множители являются безразмерными, включая сферическую функцию Y_l,m.

Видео:Квантовая механика 41 - Уравнение Шредингера. Гамильтониан.Скачать

16.7 Статистический вес энергетического уровня

Соберём воедино основные результаты, полученные в этой главе. Уровни электрона с отрицательной энергией в кулоновском поле квантуются:

,

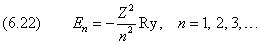
причём энергия зависит только от главного квантового числа n . Квадрат модуля момента определяется орбитальным квантовым числом l , которое при заданном уровне энергии может принимать n разных значений:

Напомним (раздел 13.5), что для краткости l часто называют абсолютной величиной момента. Существует специальная система обозначений для состояний с определённым значением l :

Видео:Спектр излучения водорода (видео 12) | Квантовая физика | ФизикаСкачать

5.3. Атом водорода

Стационарное уравнение Шредингера для водородоподобного атома (один электрон около ядра с зарядом Ze) имеет вид

Это уравнение удобно записать в сферических координатах:

Разумеется, мы не станем решать это уравнение, но просто внимательно на него посмотрим.

Заметим, что та часть уравнения (5.6), которая зависит от углов, входит только в состав оператора квадрата момента импульса (5.3). Довольно ясен физический смысл этого члена. Представим себе, что в поле центральных сил по орбите радиусом r движется классическая частица с импульсом . Ее момент количества движения равен

где — проекция импульса на направление, ортогональное радиусу-вектору . Обозначим

кинетическую энергию «ортогонального» движения. Ее можно выразить через квадрат момента количества движения:

Этот член добавляется к потенциальной энергии кулоновского притяжения к ядру, и его можно интерпретировать как потенциальную энергию в поле центробежных сил. Действительно, если — потенциальная энергия, то ее производная по r должна дать соответствующие силы:

В конечном выражении легко узнать известную из классической механики формулу для центробежной силы. Квантовая механика, как это и должно быть, воспроизводит на новом уровне результаты классической: теперь момент импульса стал оператором, но вошел на прежних правах в выражение для оператора полной энергии (гамильтониана).

Любой оператор коммутирует сам с собой, и так как оператор квадрата момента (5.3) вообще не зависит от радиальной переменной r, то

коммутирует с гамильтонианом (5.6). Кроме того, оператор проекции момента импульса

и, стало быть, с гамильтонианом. Следовательно, выполняются классические законы сохранения квадрата и одной проекции момента импульса. Эти законы сохранения справедливы для любого центрально-симметричного поля: специфика кулоновского взаимодействия пока нами не использовалась. Поэтому проекция и квадрат момента могут быть определены одновременно с энергией, и волновая функция стационарного состояния будет зависеть от квантовых чисел l и m. Однако в уравнении Шредингера (5.6) гамильтониан вовсе не зависит от оператора проекции момента импульса. Это значит, что энергия состояния не будет зависеть от магнитного квантового числа m. Иными словами, в любом центрально-симметричном поле имеется вырождение по n, кратность которого равна 21 + 1. Мы уже знаем, что источником вырождения должна служить та или иная симметрия. В классической физике движение частицы в центрально-симметричном поле всегда происходит по орбите, лежащей в одной плоскости. Но сама эта плоскость может быть произвольной в зависимости от начального положения и скорости частицы. Ясно, что значение полной энергии частицы не зависит при этом от ориентации плоскости орбиты в пространстве. Это и есть искомая симметрия, приводящая к вырождению по магнитному квантовому числу.

В кулоновском поле (равно как и в гравитационном) имеется еще одно специфическое вырождение, приводящее к тому, что энергия системы не зависит и от квантового числа l.

Вспомним опять классическую физику. В кулоновском поле финитное движение частицы совершается только по эллипсу. Возьмем в качестве аналогии искусственный спутник. Поместим его на каком-то расстоянии от Земли (то есть зададим потенциальную энергию) и придадим ему какую-то скорость (зададим кинетическую энергию). Таким образом, мы задали полную энергию спутника. Но определена ли его орбита? Разумеется, нет! При той же полной энергии направление скорости влияет на форму орбиты — от прямой линии (вертикальное падение) при нулевом моменте импульса до окружности максимально возможного радиуса при данной полной энергии. Нулевой момент соответствует чисто радиальным колебаниям сквозь центр притяжения, когда вовсе нет кругового движения, и эллипс вырождается в прямую линию (для спутника такое колебание невозможно, но микрочастицы — иное дело). Максимально возможный момент импульса достигается в обратном случае чисто круговой орбиты, когда совсем нет радиального движения. Важно, что его (максимального момента импульса) величина зависит от полной энергии спутника.

Подчеркнем, что ограничение сверху на возможную величину момента импульса — при заданной полной механической энергии — имеет чисто классическое происхождение. Убедиться в этом можно следующим образом. Запишем классическое (не квантовое) выражение для в виде

.

Здесь — кинетическая энергия радиального движения: – радиальная составляющая скорости, — эффективная потенциальная энергия, включающая в себя потенциальную энергию в поле центробежных сил. Ясно, что . Учитывая, что энергия связанных состояний меньше нуля, перепишем это неравенство в виде

или
.

Эффективная потенциальная энергия при отличном от нуля моменте импульса L имеет минимум в точке , её минимальное значение равно

.

Поскольку неравенство должно выполняться и в точке минимума, получаем

или .

Если в последнее неравенство подставить боровское выражение (3.3) для энергии водородоподобного иона и выражение (5.5) для квадрата момента, то получим неравенство

,

которое имеет решение

.

Здесь n — боровский номер стационарной орбиты, или главное квантовое число (см. ниже). Основанная на решении уравнения Шредингера (5.6) строгая квантовая теория дает тот же результат.

Итак, классическая физика подсказывает нам следующие свойства решений уравнения Шредингера:

Вооружившись знанием классической механики, мы можем смело приступать к изучению квантовой. Теперь станут понятны свойства решений уравнения Шредингера для атома водорода. Его решениями являются волновые функции, нумеруемые тремя квантовыми числами: . Про l и n уже много говорилось, а n — знакомое нам по атому Бора главное квантовое число, принимающее целые положительные значения. Разным наборам чисел отвечают разные волновые функции, общий вид которых — для любых возможных наборов чисел – нам сейчас не важен.

Рис. 5.6. Волновые функции трех первых состояний атома водорода с l = 0

Пример 1. Волновая функция основного состояния электрона в атоме водорода имеет вид

Найдем вероятности и обнаружить электрон внутри сфер с радиусами и .

Вероятность обнаружить электрон в элементе объема dV равна

Так как волновая функция основного состояния не зависит от направления радиуса-вектора , а лишь от его модуля r, то можно написать выражение для вероятности обнаружить электрон в шаровом слое радиусом r и толщиной dr. Объем этого слоя равен (площадь поверхности, умноженная на толщину). Тогда

Теперь надо проинтегрировать вероятность no всем значениям r от 0 до R, получив вероятность W(R) найти электрон внутри сферы радиусом R:

Интеграл берется точно, и в результате получаем

Здесь e — основание натурального логарифма. Разность дает вероятность найти электрон между сферами с радиусами и . Видно, что численно эта вероятность близка к вероятности . Зато вероятность обнаружить электрон за пределами сферы радиусом заметно меньше: она равна, как нетрудно догадаться,

Иными словами, с вероятностью более 76% электрон в основном состоянии пребывает на расстоянии не более двух радиусов Бора от ядра.

Пример 2. Найдем электростатический потенциал, создаваемый атомом водорода в основном состоянии.

Возьмем любую точку на расстоянии R от ядра. Электростатический потенциал в ней создается, во-первых, положительным зарядом е ядра и, во-вторых, той частью заряда электрона, которая находится внутри сферы радиусом R. Хорошо известно, что сферически симметричное распределение заряда не создает поля во внутренних областях. Поэтому часть электронного облачка, находящаяся дальше выбранной точки, не внесет вклада в потенциал. Поскольку в уравнении (5.7) вычислена вероятность W(R) нахождения электрона внутри сферы радиусом R, то отрицательный заряд внутри этой сферы равен –eW(R). Поэтому потенциал в точке R, создаваемый эффективным зарядом

На больших расстояниях потенциал (5.8) убывает экспоненциально, то есть гораздо быстрее обычного кулоновского потенциала точечного заряда. Это — так называемый эффект экранировки: отрицательный заряд электрона компенсирует положительный заряд ядра. При

потенциал (5.8) переходит в обычный кулоновский потенциал: мы проникли внутрь электронного облачка, где оно уже не экранирует заряд ядра.

Для энергии из уравнения Шредингера получается в точности такая же формула, что и из теории Бора:

Как видно, энергия действительно не зависит от квантовых чисел l, m. При этом, как следует из свойств решений уравнения (5.6), азимутальное квантовое число l принимает целые значения от 0 до n – 1. И это свойство, угаданное нами на основе классической физики, воспроизвелось в квантовой механике.

Удивительно, как квантовая механика, низвергнувшая столько классических представлений, дает аналогичные результаты там, где в дело вступают свойства симметрии системы. Отсюда вывод: симметрия играет более важную роль, чем конкретные физические законы. Когда-нибудь будут открыты новые законы, которые обобщат и квантовую механику, и все теории, которые ныне находятся на переднем крае науки. Но свойства симметрии системы так или иначе проявят себя.

Отличие квантовой механики от теории Бора — более богатая структура состояний: состояние определяется тремя квантовыми числами, как и в трехмерном потенциальном ящике. Кстати, это не случайно. Три квантовых числа в потенциальной яме и в атоме водорода — отражение трехмерности нашего пространства. Подсчитаем кратность вырождения, то есть число различных состояний с одной и той же энергией (главным квантовым числом n). При данном значении n число l пробегает все целые числа от 0 до n – 1, и каждому из них соответствует 2l + 1 значение n. Поэтому кратность вырождения N определяется соотношением

При n = 1 имеем N = 1, то есть основной уровень не вырожден. При n=2 кратность вырождения равна 4: один уровень с l = 0 и три уровня с l = 1 и различными проекциями момента импульса n = –1, 0, +1. При n = 3 кратность вырождения N = 9: один уровень с l = 0, три уровня с l = 1 и пять уровней (по числу проекций) с l = 2. Для классификации состояний энергии по значению квантового числа l применяют условные обозначения, позаимствованные из спектроскопии, где они появились еще до создания теории атома:

🔥 Видео

Структура материи 6: уравнение Шрёдингера. Зачем нужна квантовая механика – Виталий Бейлин | НаучпопСкачать

Консультация по квантовой механике. Часть 5. "Волновая функция. Уравнение Шредингера"Скачать

Урок 447. Модель атома водорода по БоруСкачать

Квантовая физика для чайников. Дмитрий ПобединскийСкачать

Уравнение Шрёдингера для атома водорода. Квантование энергии. Спектр излучения атома водорода.Скачать

Энергетические уровни атома (видео 6) | Квантовая физика | ФизикаСкачать

История создания квантовой механики #5: Шредингер и ДиракСкачать

Рубцов А. Н. - Введение в квантовую физику - Волновая функция и уравнение ШредингераСкачать

Физика 11 класс (Урок№25 - Квантовые постулаты Бора.)Скачать

Атомная физика. Лекция 14. Атом водорода. Гамильтониан и решение уравнения Шредингера.Скачать

Лекция №4 "Волновая функция. Уравнение Шредингера" (Гавриков А.В.)Скачать