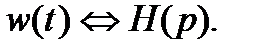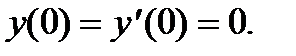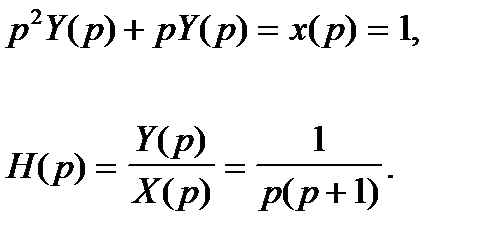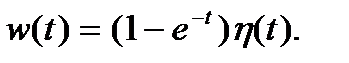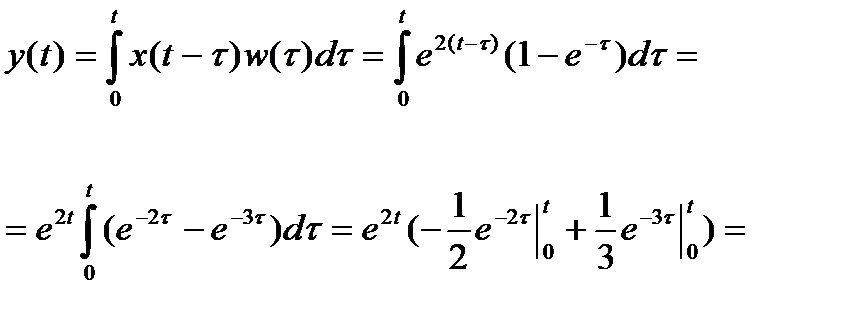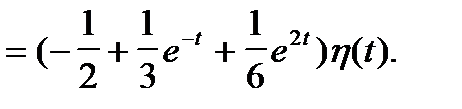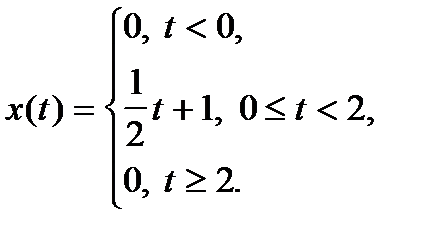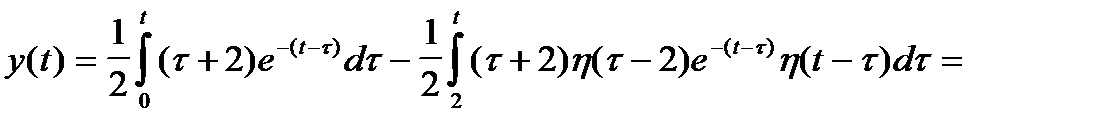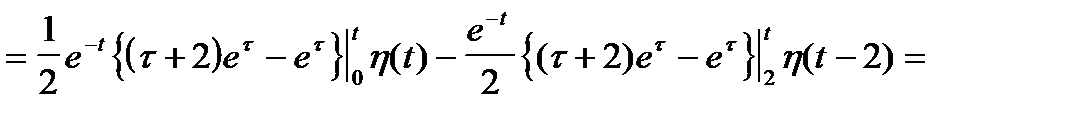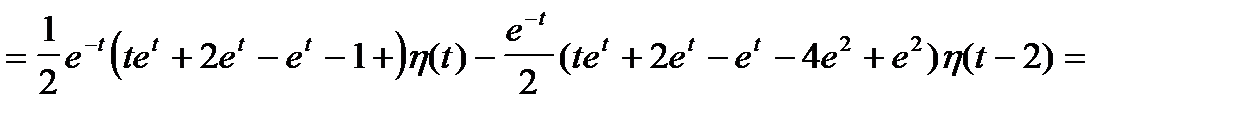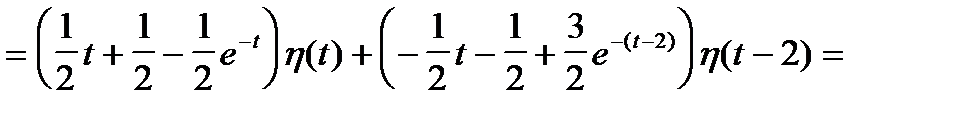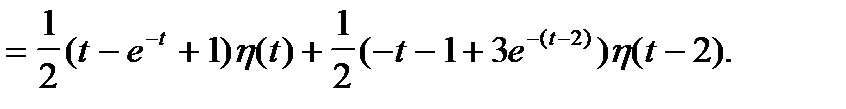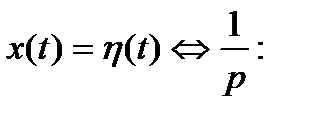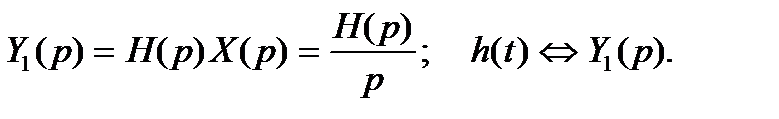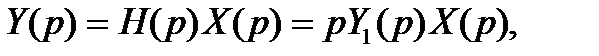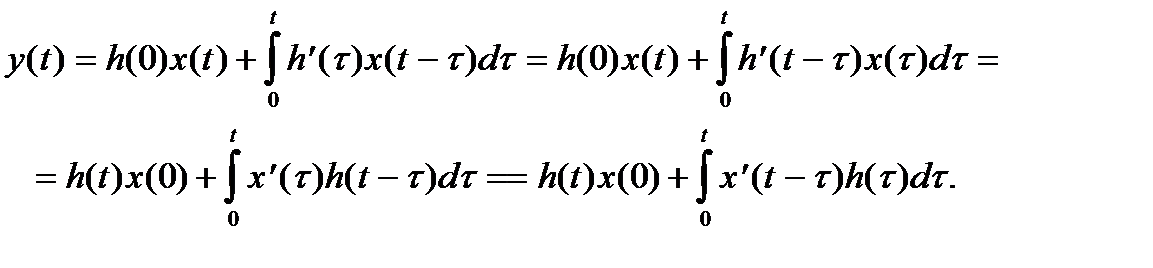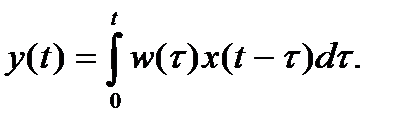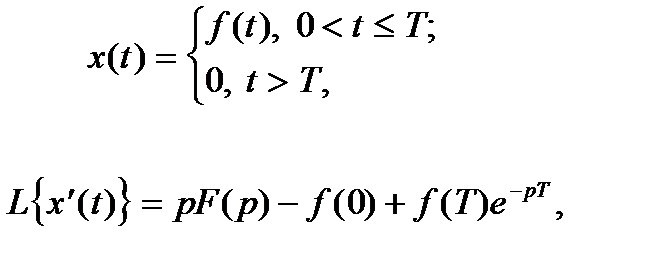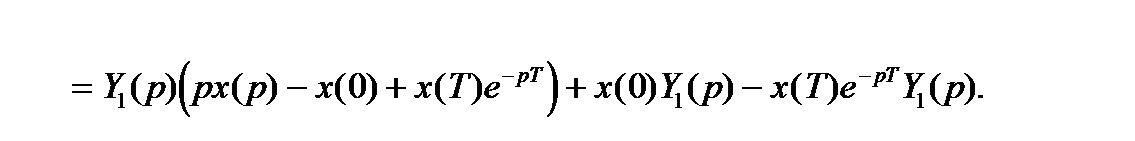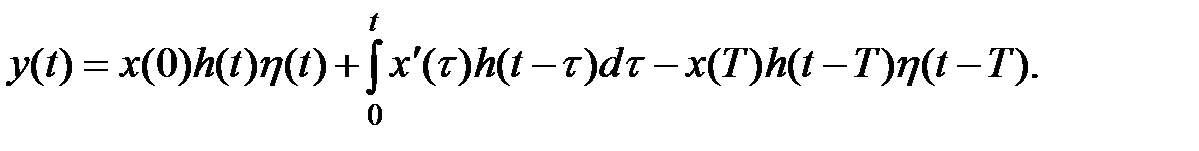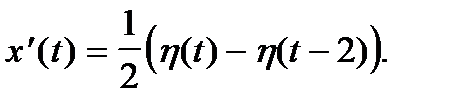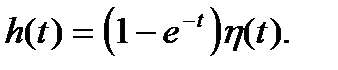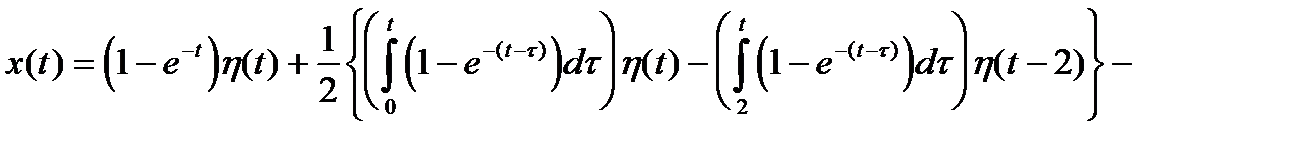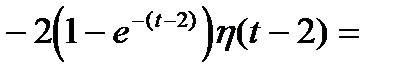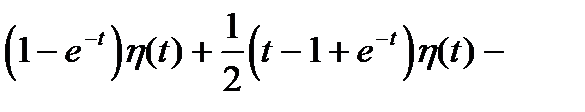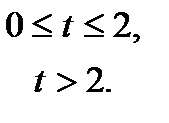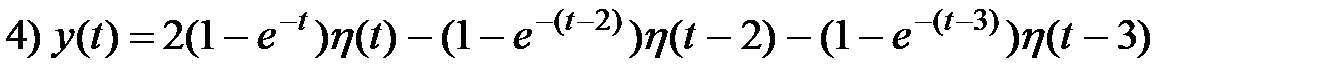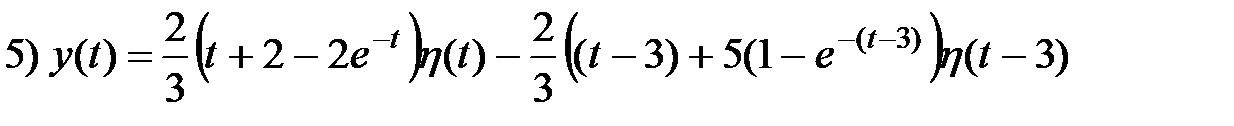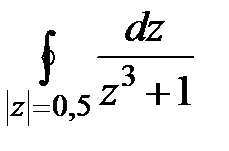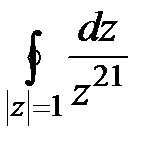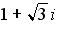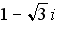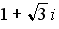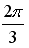Решение уравнения с помощью интеграла дюамеля (8 видео)

VMath

Содержание

Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Применения операционного исчисления
Решение задачи Коши для ОДУ с постоянными коэффициентами
Решение задачи Коши для систем линейных ДУ
Решение ОДУ с помощью интеграла Дюамеля
Решение задачи Коши с правой частью, содержащей функцию Хэвисайда
Решение задачи Коши с периодической правой частью
Решение уравнения с помощью интеграла дюамеля
Решение линейных дифференциальных уравнений методом свертки (формула Грина, формула Дюамеля)
💡 Видео

Инструменты сайта

Основное

Информация

Действия

Содержание

Видео:2020 г. Интеграл Дюамеля для анализа цепей. Лекция и практикаСкачать

Применения операционного исчисления

Видео:Решить задачу Коши для дифференциального уравнения с помощью формулы ДюамеляСкачать

Решение задачи Коши для ОДУ с постоянными коэффициентами

Пример 1.

Решить однородное дифференциальное уравнение с постоянными коэффициентами. begin &x»’+2x»+5x’=0,\ &x(0)=-1, ,, x'(0)=2, ,, x»(0)=0. end

Записываем изображения для левой и правой частей дифференциального уравнения. Для левой части используем теорему о дифференцировании оригинала: begin &x(t) risingdotseq X(p),\ &x'(t) risingdotseq pX(p)-x(0)=pX(p)+1,\ &x»(t) risingdotseq p^2X(p)-px(0)-x'(0)=p^2X(p)+p-2,\ &x»'(t) risingdotseq p^3X(p)-p^2x(0)-px'(0)-x»(0)=p^3X(p)+p^2-2p-0. end Справа стоит $0$, изображение для него тоже $0$.

Запишем уравнение с изображениями (операторное уравнение). Оно уже будет алгебраическим, а не дифференциальным: begin p^3X(p)+p^2-2p+2(p^2X(p)+p-2)+5(pX(p)+1)=0. end И найдем из него неизвестное $X(p)$: begin X(p)=-frac

. end Используя теоремы, приемы, таблицы операционного исчисления получим оригинал: begin X(p) risingdotseq x(t)=-displaystylefrac15-displaystylefrac45 e^mbox,2t+displaystylefrac35e^mbox,2t. end

Пример 2.

Решить неоднородное дифференциальное уравнение с постоянными коэффициентами. begin x»-2x’-3x=e^,\ x(0)=x'(0)=0. end

Записываем изображения для левой и правой частей дифференциального уравнения. Для левой части используем теорему о дифференцировании оригинала: begin &x(t) risingdotseq X(p),\ &x'(t) risingdotseq pX(p)-x(0)=pX(p),\ &x»(t) risingdotseq p^2X(p)-px(0)-x'(0)=p^2X(p), end Справа стоит $e^$, изображение равно $displaystylefrac$.

Запишем операторное уравнение: begin (p^2-2p-3)X(p)=frac. end Находим $X(p)$: begin X(p)=frac. end Используя, например, вторую теорему разложения, получим оригинал: begin X(p) risingdotseq displaystylefrac14,te^-displaystylefrac,e^+displaystylefrac,e^. end

Пример 3.

Решить неоднородное дифференциальное уравнение с постоянными коэффициентами. begin x»+3x’=mbox,2t,\ x(0)=2, ,, x'(0)=0. end

Пример 4.

Решить неоднородное дифференциальное уравнение с постоянными коэффициентами. begin x»+x’=e^t,\ x(1)=1, ,, x'(1)=2. end Так как начальные условия даны не при $t=0$, сразу применить теорему о дифференцировании оригинала мы не можем. Поставим вспомогательную задачу для функции $y(t)=x(t+1)$: begin y»+y’=e^,\ y(0)=1, ,, y'(0)=2. end Записываем операторное уравнение begin (p^2Y(p)-p-2)+(pY(p)-1)=displaystylefrac. end

Решаем полученное уравение: begin Y(p)=displaystylefrac+displaystylefrac

. end begin y(t)=displaystylefrac12e^+left(displaystylefrac-2right)e^+(3-e). end Со сдвигом на $1$ находим решение исходной задачи: begin x(t)=y(t-1)=displaystylefrac12e^+left(displaystylefrac-2right)e^+(3-e). end

Видео:Лекция 58. Интеграл ДюамеляСкачать

Решение задачи Коши для систем линейных ДУ

Пример 5.

Решить систему линейных дифференциальных уравнений с постоянными коэффициентами. begin left < begin&x’ = 2x+8, \ &y’ = x+4y+1, \ &x(0)=1,, y(0)=0. \ end right. end

Запишем изображения: begin begin x(t) risingdotseq X(p), & x'(t) risingdotseq p,X(p)-1, \ y(t) risingdotseq Y(p), & y'(t) risingdotseq p,Y(p). end end begin 8 risingdotseq displaystylefrac

, ,, 1 risingdotseq displaystylefrac

. end

Операторная система уравнений принимает вид: begin left < beginpX(p)-1 &= 2X(p)+displaystylefrac

, \ pY(p) &= X(p)+4Y(p)+displaystylefrac

.\ end right. end

Решаем систему, находим изображения $X(p)$, $Y(p)$ и их оригиналы $x(t)$, $y(t)$: begin X(p)=displaystylefrac

risingdotseq x(t)=-4+5e^. end begin Y(p)=displaystylefrac

risingdotseq y(t)=displaystylefrac34-displaystylefrac52,e^+displaystylefrac74,e^. end

Пример 6.

Решить систему линейных дифференциальных уравнений с постоянными коэффициентами. begin left < begin&x’ = 2x+8y, \ &y’ = x+4y+1, \ &x(0)=1,, y(0)=0.\ end right. end

begin begin x(t) risingdotseq X(p), & x'(t) risingdotseq p,X(p)-1, \ y(t) risingdotseq Y(p), & y'(t) risingdotseq p,Y(p),\ 1 risingdotseq displaystylefrac

. &\ end end

Операторная система уравнений принимает вид: begin left < beginpX(p)-1 &= 2X(p)+8Y(p), \ pY(p) &= X(p)+4Y(p)+displaystylefrac

.\ end right. end

Решаем систему находим изображения $X(p)$, $Y(p)$ и их оригиналы $x(t)$, $y(t)$: begin X(p)=displaystylefrac

risingdotseq x(t)=frac49-frac43,t+frac59,e^. end begin Y(p)=displaystylefrac

risingdotseq y(t)=-displaystylefrac+displaystylefrac13,t+displaystylefrac,e^. end

Пример 7.

Решить систему линейных дифференциальных уравнений с постоянными коэффициентами. begin left < begin&x’-2x-4y = mbox, t, \ &y’+x+2y = mbox,t, \ &x(0)=0,, y(0)=0.\ end right. end

Операторная система уравнений принимает вид: begin left < begin(p-2)X(p)-4Y(p) &= frac

, \ X(p)+(p+2)Y(p) &= frac

.\ end right. end

Решаем систему находим изображения $X(p)$, $Y(p)$ и их оригиналы $x(t)$, $y(t)$: begin X(p)=displaystylefrac

+displaystylefrac

-displaystylefrac

risingdotseq x(t)=2+4t-2,mbox,t-3,mbox,t. end begin Y(p)=-displaystylefrac

+displaystylefrac

risingdotseq y(t)=-2t+2,mbox,t. end

Видео:Решить интегральное уравнение (ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ) Свёртка функций, Умножение изображенийСкачать

Решение ОДУ с помощью интеграла Дюамеля

Введем обозначения:
Уравнение: $x^(t)+a_1,x^(t)+ldots+a_n,x(t)=f(t)$.
Начальные условия: $x(0)=x'(0)=ldots=x^=0$.
Неизвестная функция $x(t)$, имеющая изображение $X(p)$.
Сложная функция в правой части $f(t)$, имеющая изображение $F(p)$.

Запишем алгоритм решения.
1. Решается вспомогательное уравнение $$ y^(t)+a_1,y^(t)+ldots+a_n,y(t)=1.$$ С учетом начальных условий левая и правые части уравнений будут иметь изображения: begin begin y(t) & risingdotseq Y(p),\ y'(t) & risingdotseq p,Y(p),\ y»(t)& risingdotseq p^2Y(p),\ &cdots\ y^(t)& risingdotseq p^nY(p). end end Вспомогательное операторное уравнение запишем в виде: begin Y(p)cdot h(p) = frac

,\ h(p)=p^n+a_1p^+ldots+a_n. end $$Y(p) risingdotseq y(t).$$

2. Решается исходное уравнение. Левая часть уравнения совпадает с левой частью вспомогательного, поэтому операторное уравнение записывается так: $$ X(p)cdot h(p) = F(p),$$ при этом $h(p)$, используя решение вспомогательного уравнения, можно записать в виде begin h(p)=frac. end Тогда $$ X(p) = F(p),pY(p).$$ Для нахождения $x(t)$ необходимо найти оригинал для $pY(p)F(p)$, то есть вычислить интеграл из формулы Дюамеля: $$ p F(p) Y(p) risingdotseq y(0)cdot f(t)+intlimits_0^t f(tau),y'(t-tau),dtau,$$ где $y(t)$ — уже найденное решение вспомогательного уравнения.

Пример 8.

Решить задачу Коши с помощью интеграла Дюамеля. begin x»+2x’=frac<1+e^>, ,, x(0)=0, ,, x'(0)=0. end Решаем через интеграл Дюамеля в два этапа, как было описано выше.

2. Исходное уравнение в операторном виде: begin (p^2+2p)X(p)=F(p). end Правая часть этого уравнения такая же, как и для вспомогательного. Левую часть $frac<1+e^>$ обозначим $f(t)$, ее изображение $F(p)$. Тогда begin X(p)=frac

. end Решая вспомогательное уравнение, мы находили: begin (p^2+2p)Y(p)=frac

,, Rightarrow ,, p^2+2p=frac. end Тогда begin X(p)=frac<frac>=pF(p)Y(p). end

Теперь по формуле Дюамеля получаем: begin X(p)=p F(p) Y(p) risingdotseq x(t)=y(0)cdot f(t)+intlimits_0^t f(tau),y'(t-tau),dtau, end где $y(t)$ — уже найденное решение вспомогательного уравнения: begin begin & y(t)=-frac14+frac12t+frac14 e^,\ & y(0)=0,\ & y'(t-tau)=frac12-frac12e^. end end

Видео:Решить интегральное уравнениеСкачать

Решение задачи Коши с правой частью, содержащей функцию Хэвисайда

Пример 9

Решить задачу Коши, когда правая часть дифференциального уравнения содержит составную функцию (выражаемую через функцию Хэвисайда). begin left < begin&x»+x=eta(t)-eta(t-2), \ &x(0)=0,\ &x'(0)=0. end right. end

Запишем изображения для левой и правой частей уравнения: begin &x»+x risingdotseq p^2,X(p)+X(p),\ &eta(t)-eta(t-2) risingdotseq frac

-frac<e^>

. end Для правой части, содержащей функцию Хэвисайда, воспользовались теоремой запаздывания.

Находим изображение для $displaystylefrac

$ с помощью теоремы об интегрировании оригинала: begin &frac

risingdotseq mbox,t ,, Rightarrow\ &frac

risingdotseq intlimits_0^t,mbox,tau,dtau=-mbox,t+1. end Тогда изображение для $displaystylefrac<e^>

$ по теореме запаздывания будет равно: begin frac<e^>

risingdotseq (-mbox,(t-2)+1)eta(t-2). end

Решение заданного уравнения: begin x(t)= (1-mbox,t)eta(t)-(1-mbox,(t-2))eta(t-2). end

Пример 10

Решить задачу Коши, когда правая часть дифференциального уравнения задана графически (и выражается через функцию Хэвисайда). begin left < begin&x»+4x=f(t). \ &x(0)=0,\ &x'(0)=0. end right. end

Запишем аналитическое выражение для $f(t)$ с помощью функции Хэвисайда и найдем ее изображение: begin &f(t)=2teta(t)-4(t-1)eta(t-1)+2(t-2)eta(t-2),\ &F(p)=frac

(1-2e^+e^). end Операторное уравнение имеет вид: begin &X(p)(p^2+4)=frac

(1-2e^+e^),, Rightarrow\ &X(p)=frac

(1-2e^+e^). end

Для первого слагаемого найдем оригинал, разложив дробь на сумму простейших: begin frac

=frac-frac risingdotseq frac12t-frac14,mbox,2t. end Для остальных слагаемых воспользуемся теоремой запаздывания: begin X(p)risingdotseq x(t)= frac12left(t-frac12,mbox,2tright)eta(t)-\ -left((t-1)-frac12,mbox,2(t-1)right)eta(t-1)+\ +frac12left((t-2)-frac12,mbox,2(t-2)right)eta(t-2). end

Видео:13. Операционное исчисление. Решить неоднородное ДУ 2 порядкаСкачать

Решение задачи Коши с периодической правой частью

Периодическую правую часть тоже очень удобно записывать с помощью функции Хэвисайда.

Пусть $f(t)$ — периодическая с периодом $T$ функция-оригинал. Обозначим через $f_0(t)$ функцию: begin f_0(t)=begin f(t),& 0 oplaplace/seminar5_2.txt · Последние изменения: 2021/05/28 18:23 — nvr

Видео:Лекция 093-5. Импульсные переходные процессы. Интеграл ДюамеляСкачать

Решение уравнения с помощью интеграла дюамеля

Зная реакцию цепи на единичное возмущающее воздействие, т.е. функцию переходной проводимости или (и) переходную функцию по напряжению , можно найти реакцию цепи на воздействие произвольной формы. В основе метода – метода расчета с помощью интеграла Дюамеля – лежит принцип наложения.

При использовании интеграла Дюамеля для разделения переменной, по которой производится интегрирование, и переменной, определяющей момент времени, в который определяется ток в цепи, первую принято обозначать как , а вторую — как t.

Пусть в момент времени к цепи с нулевыми начальными условиями (пассивному двухполюснику ПД на рис. 1) подключается источник с напряжением произвольной формы. Для нахождения тока в цепи заменим исходную кривую ступенчатой (см. рис. 2), после чего с учетом, что цепь линейна, просуммируем токи от начального скачка напряжения и всех ступенек напряжения до момента t, вступающих в действие с запаздыванием по времени.

В момент времени t составляющая общего тока, определяемая начальным скачком напряжения , равна .

В момент времени имеет место скачок напряжения , который с учетом временного интервала от начала скачка до интересующего момента времени t обусловит составляющую тока .

Полный ток в момент времени t равен, очевидно, сумме всех составляющих тока от отдельных скачков напряжения с учетом , т.е.

Заменяя конечный интервал приращения времени на бесконечно малый, т.е. переходя от суммы к интегралу, запишем

Решение уравнения с помощью интеграла дюамеля

(1)

Соотношение (1) называется интегралом Дюамеля.

Следует отметить, что с использованием интеграла Дюамеля можно определять также напряжение. При этом в (1) вместо переходной проводимости будет входить переходная функция по напряжению.

Последовательность расчета с использованием
интеграла Дюамеля

Определение функции (или ) для исследуемой цепи.
Запись выражения (или ) путем формальной замены t на .
Определение производной .
Подстановка найденных функций в (1) и интегрирование определенного интеграла.

В качестве примера использования интеграла Дюамеля определим ток в цепи рис. 3, рассчитанный в предыдущей лекции с использованием формулы включения.

Исходные данные для расчета: , , .

Полученный результат аналогичен выражению тока, определенному в предыдущей лекции на основе формулы включения.

Метод переменных состояния

Уравнения элекромагнитного состояния – это система уравнений, определяющих режим работы (состояние) электрической цепи.

Метод переменных состояния основывается на упорядоченном составлении и решении системы дифференциальных уравнений первого порядка, которые разрешены относительно производных, т.е. записаны в виде, наиболее удобном для применения численных методов интегрирования, реализуемых средствами вычислительной техники.

Количество переменных состояния, а следовательно, число уравнений состояния равно числу независимых накопителей энергии.

К уравнениям состояния выдвигаются два основных требования:

-возможность восстановления на основе переменных состояния (переменных, относительно которых записаны уравнения состояния) любых других переменных.

Первое требование удовлетворяется специальной методикой составления уравнений состояния, которая будет рассмотрена далее.

Для выполнения второго требования в качестве переменных состояния следует принять потокосцепления (токи в ветвях с индуктивными элементами) и заряды (напряжения) на конденсаторах. Действительно, зная закон изменения этих переменных во времени их всегда можно заменить источниками ЭДС и тока с известными параметрами. Остальная цепь оказывается резистивной, а следовательно, всегда рассчитывается при известных параметрах источников. Кроме того, начальные значения этих переменных относятся к независимым, т.е. в общем случае рассчитываются проще других.

При расчете методом переменных состояния, кроме самих уравнений состояния, связывающих первые производные и с самими переменными и и источниками внешних воздействий – ЭДС и тока, необходимо составить систему алгебраических уравнений, связывающих искомые величины с переменными состояния и источниками внешних воздействий.

Таким образом, полная система уравнений в матричной форме записи имеет вид

;

(2)

(3)

Здесь и — столбцовые матрицы соответственно переменных состояния и их первых производных по времени; — матрица-столбец источников внешних воздействий; — столбцовая матрица выходных (искомых) величин; — квадратная размерностью (где n – число переменных состояния) матрица параметров, называемая матрицей Якоби; — прямоугольная матрица связи между источниками и переменными состояния (количество строк равно n, а столбцов – числу источников m); — прямоугольная матрица связи переменных состояния с искомыми величинами (количество строк равно числу искомых величин к, а столбцов – n); — прямоугольная размерностью матрица связи входа с выходом.

Начальные условия для уравнения (2) задаются вектором начальных значений (0).

В качестве примера составления уравнений состояния рассмотрим цепь на рис. 4,а, в которой требуется определить токи и .

По законам Кирхгофа для данной цепи запишем

;

(4)

;

(5)

(6)

Поскольку с учетом соотношения (6) перепишем уравнения (4) и (5) в виде

или в матричной форме записи

Матричное уравнение вида (3) вытекает из соотношений (4) и (6):

Вектор начальных значений (0)= .

Непосредственное использование законов Кирхгофа при составлении уравнений состояния для сложных цепей может оказаться затруднительным. В этой связи используют специальную методику упорядоченного составления уравнений состояния.

Методика составления уравнений состояния

Эта методика включает в себя следующие основные этапы:

1. Составляется ориентированный граф схемы (см. рис. 4,б), на котором выделяется дерево, охватывающее все конденсаторы и источники напряжения (ЭДС). Резисторы включаются в дерево по необходимости: для охвата деревом всех узлов. В ветви связи включаются катушки индуктивности, источники тока и оставшиеся резисторы.

2. Осуществляется нумерация ветвей графа (и элементов в схеме), проводимая в следующей последовательности: первыми нумеруются участки графа (схемы) с конденсаторами, затем резисторами, включенными в дерево, следующими нумеруются ветви связи с резисторами и, наконец, ветви с индуктивными элементами (см. рис. 4,б).

3. Составляется таблица, описывающая соединение элементов в цепи. В первой строке таблицы (см. табл. 1) перечисляются емкостные и резистивные элементы дерева, а также источники напряжения (ЭДС). В первом столбце перечисляются резистивные и индуктивные элементы ветвей связи, а также источники тока.

Видео:Решение разных задач по операционному исчислению.Скачать

Решение линейных дифференциальных уравнений методом свертки (формула Грина, формула Дюамеля)

Рассмотрим линейное дифференциальное уравнение в операторной форме при нулевых начальных условиях:

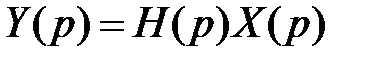
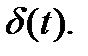
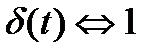
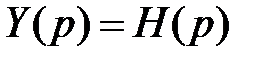
Пусть входное воздействие является импульсной функцией Поскольку , изображение выходного сигнала совпадает с передаточной функцией:

Функцией Грина (или функцией веса в теории управления) линейного дифференциального уравнения называют отклик системы на импульсное входное воздействие или оригинал передаточной функции:

Поскольку изображение выходного сигнала является произведением изображений, то и оригинал можно представить как свертку оригиналов и :

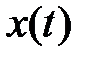
Таким образом, при известной функции Грина можно найти отклик системы на любое внешнее воздействие.

Пример 8. Найти частное решение дифференциального уравнения

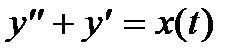
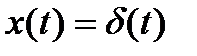
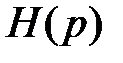
Взяв в качестве правой части импульсную функцию и переходя к изображениям, получим передаточную функцию:

Возвращаясь к оригиналам, получаем функцию Грина:

Теперь, задавая любым образом правую часть x(t), можно найти решение дифференциального уравнения.

Пусть 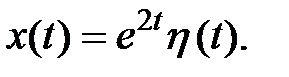Тогда

Пример 9. Найти частное решение дифференциального уравнения

, .

Правая часть уравнения задана функцией

0 2 2

x(t)

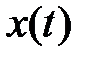
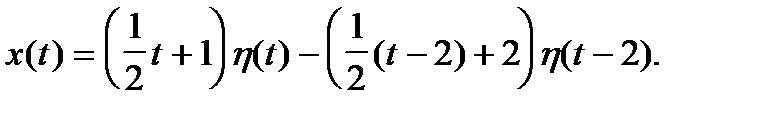
Для применения формулы свертки следует записать , используя ступенчатые функции Хевисайда:

С учетом того, что функция Грина для этого уравнения имеет вид получаем решение :

Другой способ записи решений дифференциальных линейных уравнений с использованием свертки основан на формуле Дюамеля. Характеристикой системы в этом случае служитпереходная функция , которая определяется как реакция (отклик) системы на постоянное воздействие

Из последнего выражения и свойства интегрирования оригинала следует, что функция и связаны соотношениями:

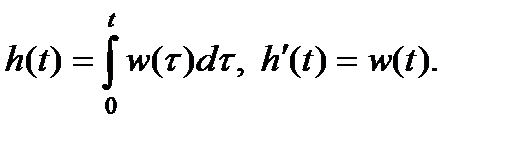
С учетом того, что

можно записать по формуле Дюамеля следующим образом:

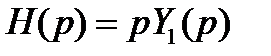
Заметим, что при условии 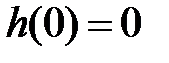две первых формы записи решения совпадают с записью

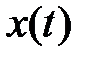
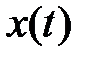
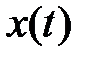
Также напомним, что в силу условий вывода формулы Дюамеля приведенные формулы можно непосредственно использовать для непрерывных функций . В том случае, если функция имеют точки разрыва первого рода, следует точно записывать эту функцию, учитывая скачкообразное изменение функции в точках разрыва или другим способом учесть эти изменения. Например, если правая часть имеет вид:

то и формула Дюамеля принимает вид:

Переходя к оригиналам, получаем

Применим формулу Дюамеля для решения примера 9.

Пример 9 (продолжение)

x¢(t)

2 t

1/2

Производная функции, стоящей в правой части уравнения равна:

Переходная функция системы имеет вид:

Тогда вычисляя по формуле

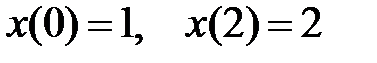
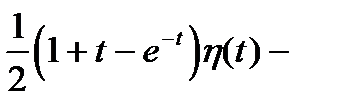
с учетом того, что , получаем:

ЗАДАЧИ

1. Решите линейные дифференциальные уравнения с использованием свертки (формула Грина, формулы Дюамеля)

а) Решите дифференциальное уравнение 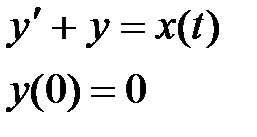для правых частей различного вида

Ответы:

b) 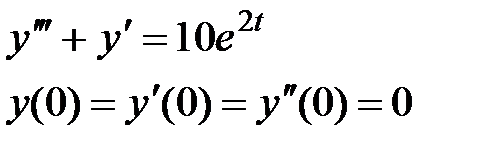f)

Контрольные вопросы:

1. Модуль и аргумент комплексного числа

2. Запись комплексного числа в показательной и тригонометрической формах

3. Степенная функция комплексного аргумента. Свойства

4. Показательная функция комплексного аргумента. Свойства

5. Логарифмическая функция комплексного аргумента. Свойства

6. Тригонометрические функции комплексного аргумента. Свойства.

7. Гиперболические функции комплексного аргумента. Свойства

8. Обратные тригонометрические функции комплексного аргумента. Свойства.

9. Обратные гиперболические функции комплексного аргумента. Свойства.

10. Понятие аналитической функции. Теорема Коши для односвязной и многосвязной областей

11. Ряд Тейлора. Область сходимости. Ряд Лорана. Область сходимости

12. Классификация изолированных особых точек.

13. Вычет аналитической функции в изолированной конечной особой точке. Вычет аналитической функции в бесконечно удаленной особой точке

14. Применение вычетов к вычислению контурных интегралов

15. Применение вычетов к вычислению несобственных интегралов

16. Определите характер особой точки 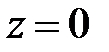для функций

17. Вычислить

18. Вычислить

19. Вычислить

20. Особенности ряда Фурье для четной и нечетной функции

21. Преобразование Лапласа. Функция-оригинал.

22.Обратное преобразование Лапласа. Теоремы разложения.

23. Решение линейных дифференциальных уравнений операторным методом

24. Формулы Грина и Дюамеля. Применение к решению линейных дифференциальных уравнений

25. Установите соответствие между комплексным числом и его модулем
1.
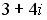
2.
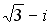
3.
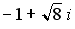
4.

Варианты ответов:

5 , 2 , 3 , 13 , ,

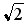
26. Установите соответствие между комплексным числом и его аргументом
1.
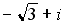
2.
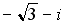
3.

Варианты ответов:

, , ,

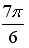
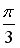
27.Установите соответствие между комплексным числом и его аргументом
1.
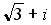
2.
3.

Варианты ответов:

, , ,

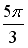
28.Установите соответствие между комплексным числом и его аргументом
1.
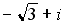
2.
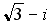
3.

Варианты ответов:

, , ,

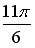
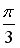
29.Установите соответствие между комплексными числами 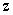и их аргументами

1.
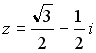
2.
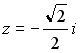
3.

Варианты ответов:

, , , ,

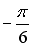
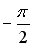
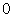
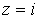
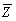
30.Произведение комплексного числа на сопряженное число равно…

31.Частное от деления двух комплексно сопряженных чисел, где , равно…

32.Дано: , тогда равно …

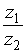
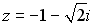
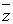
33.Произведение комплексного числа и сопряженного числа равно …

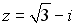
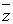
34.Произведение комплексного числа и сопряженного числа равно …

35.Значение функции в точке равно…

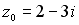
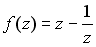
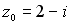
36.Значение функции в точке равно…

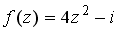
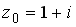
37.Значение функции в точке равно…

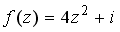
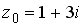
38.Значение функции в точке равно…

39.Значение функции 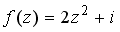в точке равно…

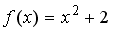
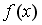
40.Дана функция , . Тогда коэффициент b₄ разложения в ряд Фурье равен…

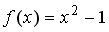
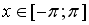
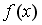
41.Дана функция , . Тогда коэффициент b₃ разложения в ряд Фурье равен…

42.Дана функция , . Тогда коэффициент а₂ разложения в ряд Фурье равен…

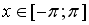
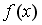
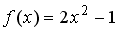
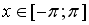
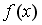
43.Дана функция , . Тогда коэффициент b₄ разложения в ряд Фурье равен…

44. Комплексное число можно представить в виде …

Варианты ответов:

Должен быть указан не менее двух вариантов ответа

1) , 2) , 3)

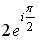
РГР № 15 (0,556 ЗЕ)

Теория вероятностей и математическая статистика

Содержание работы

1.Алгебра случайных событий.

2.Случайные величины. Законы распределений. Числовые характеристики.

3.Математическая статистика. Оценки числовых характеристик. Определения закона распределения по выборке. Критерии согласия.

4.Математическая статистика: оценка коэффициента корреляции по выборочным данным, уравнение линейной регрессии.

Список литературы [2,5,12, 15, 18 ]

Номера задач указаны согласно сборнику задач по математике для втузов

, часть 3 « Теория вероятностей и математическая статистика» под ред. Ефимова А.В.М., « Наука», 1990 (№ 15 в списке литературы, имеется в библиотеке в достаточных количествах)

1. Основные понятия. Алгебра событий. № 14.1, 14.68, 14.69, 14.70,14.5, 14.7 (14.148), 14.80,4.87, 14.139, 14.191, 14.198, 14.207, 14.208-14.211, 14.214, 14.226, 14.227, 14.231, 14.233, 14.243.

2.Случайные величины. Законы распределений. Основные характеристики.

№ 14.312, 14.313, 14.323, 14.352, 14.353, 14.354, 14.278, 14.279, 14.294, 14.297, 14.300, 14.365-14.367,14.536-14.539, 14.558, 14.559, 14.560, 14,570

3.Данные для статистической обработки (задания № 3, 4) каждый студент получает от преподавателя или получает самостоятельно (утверждает у преподавателя). Подробное рассмотрение в электронном пособии (№ 18 в списке литературы)

Лабораторная работа № 1

« Статистическое описание результатов наблюдений. Числовые оценки выборочного распределения. Интервальные оценки для математического ожидания и дисперсии. Проверка гипотезы о виде распределения»

1. Получите выборку из 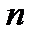чисел

2. Постройте вариационный ряд (упорядочите элементы выборки по величине). При этом можно использовать соответствующую команду на панели инструментов Excel.

3 .Представьте выборку в виде группированного статистического ряда (с.178- 181)

· определите размах выборки

· определите число интервалов группировки одним из способов:

· а) Способ 1: выбираете число интервалов , а затем находите шаг (ширину интервала группировки) , б) Способ 2: выбираете шаг (ширину интервала группировки) по формуле .

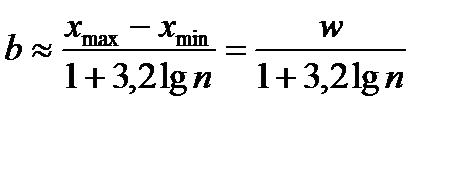
· Определите границы интервалов группировки 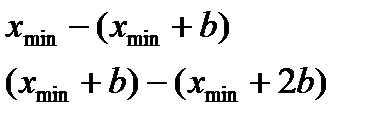, и так далее до тех пор, пока наибольший элемент выборки не попадет в последний интервал ( наилучшая ситуация, если он точно совпадает с верхней границей последнего интервала)

· Найдите середину каждого интервала

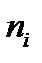
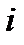
· Определите частоты — число элементов выборки, содержащихся в каждом -м интервале. При этом элемент, совпадающий с верхней границей интервала, условимся относить к следующему интервалу.

· Найдите накопленные частоты 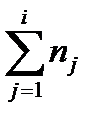. При этом сумма частот по всем интервалам должна совпадать с объемом выборки . Если сумма частот по всем интервалам не совпадает с объем выборки, то следует проверить, правильно ли найдены частоты.

· Найдите относительные частоты , которые служат оценкой вероятности попадания элемента выборки в данный интервал

· Найдите относительные накопленные частоты . Значения накопленных частот служат оценкой функции распределения и определяют эмпирическую ( выборочную) функцию распределения

· Все полученные характеристики заносим в таблицу, которую называют статистическим рядом ( табл. 1.1 на стр. 181)

Номер интервала	Границы интервала	Середина Интервала	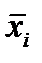Частота	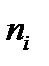Накопленная Частота	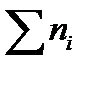Относитель- ная частота	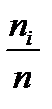Накопленная Относитель- ная частота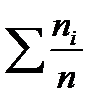
·	·	·	·	·	·	·
·	·	·	·	·	·	·

· Представить выборку графически (стр. 182-183)

· строим полигон частот— ломаную с вершинами в точках ( )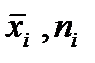

· строим полигон относительных частот— ломаную с вершинами в точках ( )

· строим гистограмму —кусочно-постоянную функцию, которая на каждом интервале группировки принимает значение . Площадь ступенчатой фигуры под графиком гистограммы равна объему выборки .

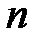
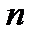
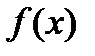
Полигон относительных частот является статистическим аналогом функции плотности вероятности. Гистограмма и полигон частот отличаются от указанной характеристики растяжением в раз. Поэтому все данные функции также являются характеристиками закона распределения генеральной совокупности .

Примечание. Все перечисленные выше операции можно провести вручную или с использованием компьютерных программ. Самое доступное математическое обеспечение – Microsoft Excel при помощи команд: . При этом карманы (интервалы группировки) надо задать отдельно.