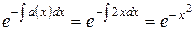Рассмотрим линейные дифференциальные уравнения первого порядка с переменными коэффициентами. Выпишем такое уравнение в общем виде:
Здесь a(x) ‑ некоторая функция аргумента x. Как мы это делали раньше, вначале будем искать решение однородного уравнения, положив функцию b(x) в правой части (5.1.12) равной нулю. Представив уравнение у¢ + a(x)y = 0 в виде
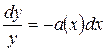
после интегрирования получаем
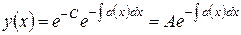
Здесь A ‑ неопределенная константа, которую можно найти из начального условия y(0) = 0.
Пример. Решить уравнение y’ + 2xy = 0 при начальном условии y(0) = 3.
a(x) = 2x,
и начальное условие определяет A = 3. Искомое решение имеет вид
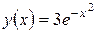
Перейдем к решению неоднородного линейного дифференциального уравнения первого порядка с переменными коэффициентами. Положим в формуле (5.1.13) A = A(x), то есть будем считать множитель A некоторой функцией от x. Этот метод называется методом вариации произвольной постоянной, и с его помощью мы попытаемся решить уравнение (5.1.12) при условии, что b(x) есть некоторая функция, не равная тождественно нулю. Из формулы (5.1.13) получаем:
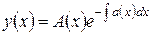
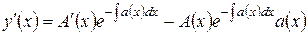
После подстановки этих выражений уравнение (5.1.12) принимает вид
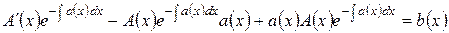
откуда следует уравнение относительно функции 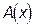
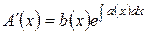
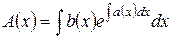
Подставив это выражение в (5.1.13), получим общее решение уравнения (5.1.12):
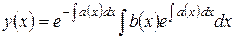
Пример. Решить уравнение 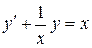
Для решения поставленной задачи можно было бы воспользоваться формулой (5.1.14), но мы пойдем другим путем: применим метод решения уравнений, которым была получена формула (5.1.14).
В нашем уравнении 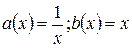
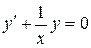
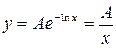
Реализуем теперь вариацию произвольной константы A, считая, что A = A(x) есть некоторая функция аргумента x. Тогда 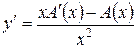
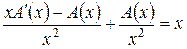
откуда следует, что A¢(x) = x 2 или 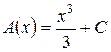
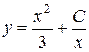
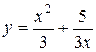
Упражнения
1.Решить дифференциальные уравнения
| 1) | 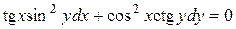 ; ; | 2) | 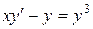 ; ; |
| 3) | 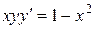 ; ; | 4) | 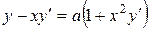 ; ; |
| 5) | 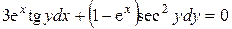 ; ; | 6) | 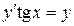 ; ; |
| 7) | 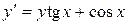 ; ; | 8) | 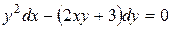 ; ; |
| 9) | 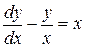 ; ; | 10) | 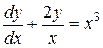 . . |
| 11) | 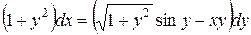 ; ; | 12) | 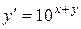 ; ; |
| 13) | 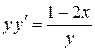 ; ; | 14) | 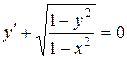 ; ; |
| 15) | 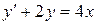 ; ; | 16) | 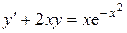 ; ; |
Раздел 6. Ряды и интеграл Фурье
Основные сведения
Функция f(x), определенная на всей числовой оси называется периодической, если существует такое число 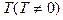
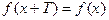
Отметим некоторые с в о й с т в а этой функции:
1) Сумма, разность, произведение и частное периодических функций периода Т есть периодическая функция периода Т.
2) Если функция f(x) период Т , то функция f(ax) имеет период 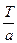
3) Если f(x) — периодическая функция периода Т , то равны любые два интеграла от этой функции, взятые по промежуткам длины Т (при этом интеграл существует), т. е. при любых a и b справедливо равенство 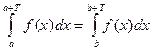
Видео:2. Линейные уравнения с переменными коэффициентамиСкачать

ЛДУ с переменными коэффициентами. Метод Лагранжа
Видео:Практика 11 Линейные ОДУ порядка n с переменными коэффициентамиСкачать

Линейные дифференциальные уравнения с переменные коэффициентами
Если известно частное решение уравнения
то его порядок можно понизить на единицу (не нарушая линейности уравнения), полагая , где — новая неизвестная функция, а затем делая замену (можно непосредственно делать замену ).
Если известно частных линейно независимых решений уравнения (32), то порядок уравнения может быть понижен на единиц.
Общее решение уравнения
есть сумма какого-нибудь его частного решения и общего решения соответствующего однородного уравнения (32).
Если известна фундаментальная система соответствующего однородного уравнения (32), то общее решение неоднородного уравнения (33) может быть найдено методом вариации постоянных ( метод Лагранжа ).
Общее решение уравнения (32) имеет вид
где — произвольные постоянные.
Будем искать решение уравнения (33) в виде
где — некоторые пока неизвестные функции от . Для их определения получаем систему
Разрешая эту систему относительно , получаем
где — произвольные постоянные. Внося найденные значения в (34), получаем общее решения уравнения (33).
В частности, для уравнения второго порядка
Решая (36) относительно и , получаем
где и — постоянные интегрирования.
Замечание. Для уравнения , где , система (36) будет выглядеть так:
Пример 1. Найти общее решение уравнения , если есть его частное решение.
Решение. Положим , где — новая неизвестная функция от , тогда
Подставляя в данное уравнение, получаем
Но так как есть частное решение данного уравнения, то , поэтому имеем
Но , а значит , и уравнение (37) примет вид
Перепишем его в виде . Отсюда имеем , откуда
Интегрируя это уравнение, найдем и, следовательно, общее решение данного уравнения будет
Пример 2. Найти общее решение уравнения .
Решение. Общее решение соответствующего однородного уравнения имеет вид (см. пример 1)
и следовательно, его фундаментальная система решений будет
Будем искать общее решение данного уравнения методом вариации произвольных постоянных:
где — постоянные неизвестные функции от , подлежащие определению. Для их нахождения составим следующую систему:
Отсюда находим: . Интегрируя, получаем
Подставляя эти значения и в выражение для , найдем общее решение данного уравнения
Пример 3. Решить уравнение .
Решение. Соответствующее однородное уравнение будет . Его характеристическое уравнение имеет мнимые корни , и общее решение однородного уравнения имеет вид
Общее решение исходного уравнения ищем в виде
где и — неизвестные функции от . Для их нахождения составим систему
Разрешаем эту систему относительно и :
Подставляя выражения и в (38), получаем общее решение данного уравнения
Здесь есть частное решение исходного неоднородного уравнения.
Пример 4. Зная фундаментальную систему решений соответствующего однородного уравнения, найти частное решение уравнения
Решение. Применяя метод вариации постоянных, находим общее решение уравнения (39):
При первые два слагаемых правой части (40) стремятся к бесконечности, причем при любых , неравных нулю одновременно, функция есть бесконечно большая функция при . Третье слагаемое правой части (40) имеет пределом ноль при , что легко установить с помощью правила Лопиталя. Таким образом, функция , которая получается из (40) при и , будет решением уравнения (39), удовлетворяющим условию .
Видео:ЛОДУ с переменными коэффициентами. Примеры.Скачать

Составление дифференциального уравнения по заданной фундаментальной системе решений
Рассмотрим линейно независимую на отрезке систему функций
имеющих все производные до n-го порядка включительно. Тогда уравнение
где — неизвестная функция, будет линейным дифференциальным уравнением, для которого, как нетрудно видеть, функции составляют фундаментальную систему решений. Коэффициент при в (42) есть определитель Вронского системы (41). Те точки, в которых этот определитель обращается в ноль, будут особыми точками построенного уравнения — в этих точках обращается в ноль коэффициент при старшей производной .
Пример 1. Составить дифференциальное уравнение, для которого образуют фундаментальную систему решений.
Решение. Применяя формулу (42), получаем
Раскрывая определитель в левой части (43) по элементам третьего столбца, будем иметь . Это и есть искомое дифференциальное уравнение.
Пример 2. Составить дифференциальное уравнение, для которого функции фундаментальную систему решений образуют функции .
Решение. Составим уравнение вида (42):
Раскрывая последний определитель по элементам 3-го столбца, будем иметь
В этом примере определитель Вронского обращается в ноль при . Это не противоречит общей теории, в силу которой определитель Вронского фундаментальной системы решений линейного однородного дифференциального уравнения
с непрерывными на отрезке коэффициентами не обращается в ноль ни в одной точке отрезка . Записав уравнение (44) в виде
видим, что коэффициент при терпит разрыв при , так что в точке непрерывность коэффициентов уравнения (45) нарушается.
Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Разные задачи
Пусть — фундаментальная система линейного однородного уравнения
Тогда имеет место формула Остроградского–Лиувилля
где — определитель Вронского, а — любое значение из отрезка , на котором непрерывны коэффициенты уравнения.
Пример 1. Показать, что линейное дифференциальное уравнение имеет решение вида , где — некоторый многочлен. Показать, что второе решение этого уравнения имеет вид , где — также многочлен.
Решение. Будем искать решение в виде многочлена, например, первой степени: . Подставляя в уравнение, найдем, что . Пусть , тогда ;. таким образом, многочлен будет решением данного уравнения. Перепишем данное уравнение в виде
Пусть — второе частное решение данного уравнения, линейно независимое с первым. Находим определитель Вронского системы решений
здесь . Применяя формулу Остроградского–Лиувилля, будем иметь
где — любое значение , причем , или ; здесь . Для нахождения получили линейное дифференциальное уравнение первого порядка. Деля обе части этого уравнения на , приведем его к виду
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Решение уравнения с переменными коэффициентами
Линейным называется дифференциальное уравнение n -го порядка , если оно 1-ой степени относительно искомой функции y ( x ) и ее производных 
Если коэффициент P 0 ( x ) ≠ 1, то на него можно поделить и после соответствующих переобозначений получить:
Уравнение (8.43) называется уравнением с переменными коэффициентами. Предположим, что в нем функции 

Примечание. Частным случаем (8.43) является линейное дифференциальное уравнение 2-го порядка с переменными коэффициентами:
Если в уравнении (8.43) f ( x ) ≡ 0, то оно называется однородным, если f ( x ) ≠ 0, то неоднородным.
Теорема 8.3 (о структуре общего решения линейного неоднородного ДУ). Общее решение линейного неоднородного дифференциального уравнения представляет собой сумму общего решения соответствующего однородного и некоторого частного решения неоднородного уравнения 
Однородное дифференциальное уравнение, соответствующее неоднородному уравнению (8.43), имеет вид:
Пусть в уравнении (8.45) функции 
и называется линейным однородным дифференциальным уравнением n -го порядка с постоянными коэффициентами , где 
Рассмотрим решения уравнений (8.45) и (8.46). Обозначим полную совокупность их линейно независимых решений через 
где ci – константы интегрирования.
Перейдем к конструированию функций 
где 
– также решение уравнений (8.45) и (8.46).
Рассмотрим одну из функций (8.48) – функцию y = e λx как решение для уравнения (8.46) с постоянными коэффициентами. Продифференцируем ее n раз:
Так как e λx ≠ 0 , то 
–алгебраическое уравнение n -ой степени относительно λ, называемое характеристическим уравнением для уравнения (8.46). Известно, что уравнение n -ой степени имеет равно n корней как действительных, так и комплексных, с учетом их кратности. Значит, характеристическое уравнение (8.50) дает нам n значений числа λ, ранее обозначенных нами через 
Рассмотрим наиболее распространенный частный случай уравнения (8.46) – его аналог 2-го порядка:
Для данного уравнения характеристическое уравнение (8.50) принимает вид:
Уравнение (8.52) является квадратным относительно λ. В зависимости от дискриминанта D характеристического уравнения рассматривают три случая, приведенных в таблице 8.1.

Пример 8.17. Найти общее решение уравнений:
а) Составляем характеристическое уравнение λ 2 +2 λ – 15 = 0. Корнями этого уравнения будут λ 1 = –5 и λ 2 = 3 . Тогда, применяя (8.53), получаем общее решение: y=C 1 e – 5x +C 2 e 3x .
б) Составляем характеристическое уравнение λ 2 – 16 λ + 64 = 0.
Решая это уравнение, получим λ 1 = λ 2 = 8 . Так как корни равные, то, применяя (8.54), будем иметь:
в) Характеристическое уравнение λ 2 – 4 λ + 13 = 0 имеет комплексные корни λ 1 = 2+3 i и λ 2 = 2 –3 i . Положив в (8.55) α=2 и β = 3, получим общее решение: 
г) Характеристическое уравнение λ 2 +9 = 0 имеет корни λ 1;2 = ± 3 i . П олагая в (8.55) α=0 и β = 3, получим общее решение
Рассмотрим теперь линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами:
Теорема 8.4. Пусть задано линейное дифференциальное неоднородное уравнение второго порядка с постоянными коэффициентами и п равой частью специального вида
1. Если 
где 
2. Если 

Рассмотрим в таблице 8.2 некоторые случаи составления частного решения линейного неоднородного дифференциального уравнения (8.57) по специальному виду его правой части.
Пример 8.18. Найти общее решение уравнения 
Решение. Найдем общее решение соответствующего однородного ДУ: 
Пример 8.19. Решить уравнение 
уравнения 

Находим частное решение y ч.н. . Правая часть неоднородного уравнения в нашем случае имеет вид
Отсюда, сравнивая коэффициенты при косинусе и синусе, имеем 

Пример 8.20. Найти частное решение уравнения 

Решение . Находим общее решение однородного уравнения 
В правой части заданного уравнения имеется показательная функция. Так как в данном случае α=2 совпадает с одним из корней характеристического уравнения, то частное решение следует искать в виде функции Axe 2 x . Таким образом, y ч.н. = Axe 2 x . Дифференцируя дважды это равенство, по лучим: 

Используя начальные условия, определим значения произвольных постоянных C 1 и C 2 . Дифференцируя общее решение (8.60), получим:
Подставим в общее решение (8.60) значения x = 0 и y = 2, будем иметь 2 = C 1 + C 2 . Подставим в выражение для 



Теорема 8.5 (о наложении решений). Если правая часть уравнения (8.56) представляет собой сумму двух функций: 


является частным решением данного уравнения
📸 Видео
Линейное уравнение с двумя переменными. 7 класс.Скачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

Однородное линейное дифференциальное уравнение. Алгоритм решенияСкачать

ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать