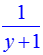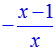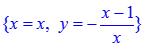Решение уравнения с параметром maple (7 видео)

Решение уравнения с параметром maple

Решение обыкновенных уравнений.

Для решения уравнений в Maple существует универсальная команда solve(eq,x) , где eq – уравнение, x – переменная, относительно которой уравнение надо разрешить. В результате выполнения этой команды в строке вывода появится выражение, которое является решением данного уравнения. Например:

Если уравнение имеет несколько решений, которые вам понадобятся для дальнейших расчетов, то команде solve следует присвоить какое-нибудь имя name . Обращение к какому-либо k –ому решению данного уравнения производится указанием его имени с номером решения k в квадратных скобках: name[k] . Например:

Решение систем уравнений.

Системы уравнений решаются с помощью такой же команды solve(,) , только теперь в параметрах команды следует указывать в первых фигурных скобках через запятую уравнения, а во вторых фигурных скобках перечисляются через запятую переменные, относительно которых требуется решить систему. Если вам будет необходимо для дальнейших вычислений использовать полученные решения уравнений, то команде solve следует присвоить какое-нибудь имя name . Затем выполняется присвоения команда assign(name) . После этого над решениями можно будет производить математические операции. Например:

Численное решение уравнений.

Для численного решения уравнений, в тех случаях, когда трансцендентные уравнения не имеют аналитических решений, используется специальная команда fsolve(eq,x) , параметры которой такие же, как и команды solve . Например:

Решение рекуррентных и функциональных уравнений.

Команда rsolve(eq,f) позволяет решить рекуррентное уравнение eq для целой функции f . Можно задать некоторое начальное условие для функции f(n) , тогда получиться частное решение данного рекуррентного уравнения. Например:

Универсальная команда solve позволяет решать функциональные уравнения, например:

F := proc ( x ) RootOf(_ Z ^2 — 3*_ Z + 2* x ) end

В результате получается решение в неявном виде. Однако Maple может работать с такими решениями. Неявное решение функционального уравнения можно попытаться преобразовать в какую-либо элементарную функцию с помощью команды convert . Продолжая приведенный выше пример, можно получить решение в явном виде:

Решение тригонометрических уравнений.

Команда solve , примененная для решения тригонометрического уравнения, выдает только главные решения, то есть решения в интервале [0,2 p ]. Для того, чтобы получить все решения, следует предварительно ввести дополнительную команду _EnvAllSolutions:=true. Например:

В Maple символ _ Z

обозначает константу целого типа, поэтому решение данного уравнения в привычной форме имеет вид , где n – целые числа.

Решение трансцендентных уравнений.

При решении трансцендентных уравнений для получения решения в явном виде перед командой solve следует ввести дополнительную команду _EnvExplicit:=true . Пример решения сложной системы трансцендентных уравнений и упрощения вида решений:

Содержание

Maple. Решение алгебраических задач. Решения уравнений, систем уравнений и неравенств в Maple
Страницы работы
Содержание работы
Решение уравнения с параметром maple
1 уЙУФЕНЩ ЛПНРШАФЕТОПК БМЗЕВТЩ
Maple ЛБЛ УХРЕТЛБМШЛХМСФПТ
юЙУМБ Й ЛПОУФБОФЩ
пРЕТБФПТЩ
рЕТЕНЕООЩЕ
уФБОДБТФОЩЕ ЖХОЛГЙЙ
рТЕПВТБЪПЧБОЙЕ НБФЕНБФЙЮЕУЛЙИ ЧЩТБЦЕОЙК
тЕЫЕОЙЕ ХТБЧОЕОЙК
пВЩЛОПЧЕООЩЕ ХТБЧОЕОЙС
уЙУФЕНЩ ХТБЧОЕОЙК
юЙУМЕООПЕ ТЕЫЕОЙЕ ХТБЧОЕОЙК
тЕЫЕОЙЕ ФТЙЗПОПНЕФТЙЮЕУЛЙИ ХТБЧОЕОЙК
🎥 Видео

Видео:Уравнения с параметром. Алгебра, 8 классСкачать

Maple. Решение алгебраических задач. Решения уравнений, систем уравнений и неравенств в Maple

Страницы работы

Содержание работы

Решение алгебраических задач

Решение уравнений (часть 1)

Для решения уравнений, систем уравнений и неравенств в Maple используется команда (оператор) «solve». Например, для решения уравнения х2 – 6х + 5 = 0 набираем: > solve(x^2–6*x+5=0); 1, 5 Обратите внимание, что если аргумент solve не является уравнением (или неравенством), то Maple трактует его так, как если бы это выражение было приравнено к 0. Можно было бы написать «> solve(x^2–6*x+5);». При решении алгебраических уравнений Maple приводит все корни, включая комплексные: > solve(x^4=1); 1, –1, I, –I

Решение уравнений (часть 2)

С помощью команды «solve» можно решать не только алгебраические уравнения. Например, решим тригоно-метрическое уравнение tg x – 2 sin x = 0: > solve(tan(x)–2*sin(x)); Обратите внимание, что Maple привёл решения, лежащие в пределах одного промежутка периодичности (от –π до π). Для вывода всех решений необходимо присвоить зарезервированной переменной _EnvAllSolutions значение true: > _EnvAllSolutions := true; > solve(tan(x)–2*sin(x)); где _Z

обозначает любое целое число.

Решение уравнений (часть 3)

Приведём примеры применения функции «solve» для решения уравнений с несколькими переменными. Решим, например, уравнение xy + x – 1 = 0 относительно x: > solve(x*y+x–1,x); относительно y: > solve(x*y+x–1,у); В общем виде Maple решает это уравнение так: > solve(x*y+x–1); Видно, что форма ответа определяется вторым параметром (или его отсутствием) команды «solve», указывающим, относительно какой переменной решать уравнение.

Неравенства решаются тем же оператором «solve». Например, решим неравенство x2(x – 1) solve(x^2*(x–1) solve(x^2*(x–1)>=0); 0, RealRange(1, ∞) В переводе на математический язык ответ: U[1; ∞). Открытый интервал (или луч) задаётся в Maple с помощью функции «Open», применяемой к концам интервала, задаваемого функцией «RealRange».

Решение системы уравнений

Все уравнения системы записываются в фигурных скобках через запятую. Решим например систему > solve(); , Решим систему с параметром > solve(,);

Видео:Уравнения с параметром. Алгебра 7 класс.Скачать

Решение уравнения с параметром maple

уМЕДХАЭБС: task2, рТЕДЩДХЭБС: Top, чЧЕТИ: Top

Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

1 уЙУФЕНЩ ЛПНРШАФЕТОПК БМЗЕВТЩ

Maple – УРЕГЙБМЙЪЙТПЧБООЩК НБФЕНБФЙЮЕУЛЙК РБЛЕФ, ЛПФПТЩН РПМШЪХАФУС РТПЖЕУУЙПОБМШОЩЕ НБФЕНБФЙЛЙ ЧП ЧУЕН НЙТЕ. рПДПВОЩЕ РБЛЕФЩ ФБЛЦЕ ОБЪЩЧБАФУС УЙУФЕНБНЙ ЛПНРШАФЕТОПК БМЗЕВТЩ. йЪ НОПЦЕУФЧБ РПДПВОЩИ УЙУФЕН (Maple, Matlab, Mathcad, Mathematica, Macsyma, Derive, Axiom, MuPAD) Maple СЧМСЕФУС РТЙЪОБООЩН МЙДЕТПН Ч ПВМБУФЙ УЙНЧПМШОЩИ ЧЩЮЙУМЕОЙК (ФП ЕУФШ Ч РТЕПВТБЪПЧБОЙЙ ЧЩТБЦЕОЙК У ЙУРПМШЪПЧБОЙЕН РЕТЕНЕООЩИ, НОПЗПЮМЕОПЧ, ЖХОЛГЙК Й Ф.Д.). рПНЙНП ЬФПЗП Ч Maple ЧИПДСФ НПДХМЙ, ПВМЕЗЮБАЭЙЕ ТБВПФХ Ч ФБЛЙИ ТБЪДЕМБИ НБФЕНБФЙЛЙ, ЛБЛ ЧЩУЫБС БМЗЕВТБ, МЙОЕКОБС БМЗЕВТБ, БОБМЙФЙЮЕУЛБС ЗЕПНЕФТЙС, ФЕПТЙС ЮЙУЕМ, НБФЕНБФЙЮЕУЛЙК БОБМЙЪ, ДЙЖЖЕТЕОГЙБМШОЩЕ ХТБЧОЕОЙС, ЛПНВЙОБФПТОЩК БОБМЙЪ, ФЕПТЙС ЧЕТПСФОПУФЕК, УФБФЙУФЙЛБ Й НОПЗЙИ ДТХЗЙИ.

дМС РПМХЮЕОЙС УРТБЧЛЙ РП ФПК ЙМЙ ЙОПК ЛПНБОДЕ ОЕПВИПДЙНП Ч ПЛОЕ Maple ЧЧЕУФЙ ?command (ЪБНЕОЙЧ command ОБ ЙНС ЛПНБОДЩ).

Maple ЛБЛ УХРЕТЛБМШЛХМСФПТ

ч ТБВПЮЕН МЙУФЕ (worksheet) УЙУФЕНЩ Maple НПЦОП ЧЧПДЙФШ ЛПНБОДЩ РПУМЕ РТЙЗМБЫЕОЙС » > «. лПНБОДБ ДПМЦОБ ЪБЧЕТЫБФШУС УЙНЧПМПН » ; «, ЕЕ ТЕЪХМШФБФ ОЕНЕДМЕООП ЧЩЧПДЙФУС ОБ ЬЛТБО. еУМЙ ЧНЕУФП » ; » РПУФБЧЙФШ » : «, ФП ЛПНБОДБ ВХДЕФ ЧЩРПМОЕОБ, ОП ТЕЪХМШФБФ ЕЕ ТБВПФЩ ОЕ ВХДЕФ ОБРЕЮБФБО. оБРТЙНЕТ:

лБЛ НЩ ЧЙДЙН, Maple ЧЩДБЕФ ПФЧЕФ Ч ФПЮОПН ЧЙДЕ Ч ЧЙДЕ ТБГЙПОБМШОПЗП ЧЩТБЦЕОЙС. еУМЙ ИПЮЕФУС РТЕДУФБЧЙФШ ЕЗП Ч ЧЙДЕ ДЕУСФЙЮОПК ДТПВЙ (У ОЕЛПФПТПК ФПЮОПУФША) ЧПУРПМШЪХКФЕУШ ЖХОЛГЙЕК evalf . еЕ РЕТЧЩК ПВСЪБФЕМШОЩК РБТБНЕФТ – ЧЩЮЙУМСЕНПЕ ЧЩТБЦЕОЙЕ, ЧФПТПК (ОЕПВСЪБФЕМШОЩК) – ЛПМЙЮЕУФЧП ЪОБЮБЭЙИ ДЕУСФЙЮОЩИ ЪОБЛПЧ (ХЮФЙФЕ, ЮФП РТЙ ЬФПН ЧЩТБЦЕОЙЕ ПЛТХЗМСЕФУС ДМС ЧЩЧПДБ УППФЧЕФУФЧХАЭЕЗП ЛПМЙЮЕУФЧБ ЪОБЛПЧ):

уЙНЧПМ % ПВПЪОБЮБЕФУС РПУМЕДОЕЕ ЧЩЮЙУМЕООПЕ Maple ЧЩТБЦЕОЙЕ, %% – РТЕДРПУМЕДОЕЕ, %%% — РТЕДРТЕДРПУМЕДОЕЕ (Б ЧПФ ПВПЪОБЮЕОЙС %%%% ХЦЕ ОЕ УХЭЕУФЧХЕФ).

юЙУМБ Й ЛПОУФБОФЩ

еУМЙ Ч ЧЩТБЦЕОЙЙ ЧУФТЕЮБЕФУС ЮЙУМП, ЪБРЙУБООПЕ У РМБЧБАЭЕК ФПЮЛПК (ОБРТЙНЕТ, 3.14 ЙМЙ 5.6e-17 ), ФП ЧУЕ ЧЩЮЙУМЕОЙС ЧЩРПМОСАФУС РТЙВМЙЦЕООП, Ч РТПФЙЧОПН УМХЮБЕ ЧЩЮЙУМЕОЙС РТПЧПДСФУС ФПЮОП. ч Maple ЕУФШ УМЕДХАЭЙЕ ЛПОУФБОФЩ: Pi юЙУМП РЙ
I нОЙНБС ЕДЙОЙГБ i
exp(1) пУОПЧБОЙЕ ОБФХТБМШОЩИ МПЗБТЙЖНПЧ e
infinity вЕУЛПОЕЮОПУФШ
true мПЗЙЮЕУЛБС ЙУФЙОБ
false мПЗЙЮЕУЛБС МПЦШ

чЩЮЙУМЕОЙС У ХЮБУФЙЕН ЛПОУФБОФ ЧЩРПМОСАФУС ФПЮОП (ЕУМЙ ФПМШЛП ЙИ ЪОБЮЕОЙЕ ОЕ ВХДЕФ РЕТЕЧЕДЕОП Л ДЕКУФЧЙФЕМШОПНХ ЪОБЮЕОЙА), ОБРТЙНЕТ

пРЕТБФПТЩ

ч Maple УХЭЕУФЧХАФ УМЕДХАЭЙЕ ПРЕТБФПТЩ:

бТЙЖНЕФЙЮЕУЛЙЕ: + , — , * , / , ^ (ЧПЪЧЕДЕОЙЕ Ч УФЕРЕОШ), ! (ЖБЛФПТЙБМ).

мПЗЙЮЕУЛЙЕ: , > , >= , , = (ТБЧОП), (ОЕ ТБЧОП).

рЕТЕНЕООЩЕ

рЕТЕНЕООПК СЧМСЕФУС МАВПК ЙДЕОФЙЖЙЛБФПТ (УПУФПСЭЙК ЙЪ МБФЙОУЛЙИ ВХЛЧ Й ГЙЖТ, ОБЮЙОБАЭЙКУС У ГЙЖТЩ). рЕТЕНЕООПК НПЦЕФ ВЩФШ РТЙУЧПЕОП МАВПЕ ЪОБЮЕОЙЕ РТЙ РПНПЭЙ ПРЕТБФПТБ РТЙУЧБЙЧБОЙС := . рЕТЕНЕООБС, ЛПФПТПК ОЕ РТЙУЧПЕОП ОЙЛБЛПЕ ЪОБЮЕОЙЕ УЮЙФБЕФУС УЧПВПДОПК РЕТЕНЕООПК Й ЕЕ ЙНС УПИТБОСЕФУС Ч БТЙЖНЕФЙЮЕУЛЙИ ЧЩЮЙУМЕОЙСИ. оБРТЙНЕТ:

уФБОДБТФОЩЕ ЖХОЛГЙЙ

ъОБЛ x (ЧПЪЧТБЭБЕФ 1, -1 ЙМЙ 0) – sign(x)

фТЙЗПОПНЕФТЙЮЕУЛЙЕ ЖХОЛГЙЙ: sin(x) , cos(x) , tan(x) , cot(x)

пВТБФОЩЕ ФТЙЗПОПНЕФТЙЮЕУЛЙЕ: arcsin(x) , arccos(x) , arctan(x) , arccot(x)

оБФХТБМШОЩК, ДЕУСФЙЮОЩК МПЗБТЙЖН Й МПЗБТЙЖН РП ДБООПНХ ПУОПЧБОЙА: ln(x) , log10(x) , log[a](x)

рТЕПВТБЪПЧБОЙЕ НБФЕНБФЙЮЕУЛЙИ ЧЩТБЦЕОЙК

ч ЧЩТБЦЕОЙЕ НПЗХФ ЧИПДЙФШ ЛПОУФБОФЩ, УЧПВПДОЩЕ РЕТЕНЕООЩЕ, НБФЕНБФЙЮЕУЛЙЕ ЖХОЛГЙЙ. рТЙНЕТ ЧЩТБЦЕОЙС:

дПЧПМШОП ЮБУФП Ч ЛБЮЕУФЧЕ ЧЩТБЦЕОЙК ЧЩУФХРБАФ НОПЗПЮМЕОЩ ПФ ПДОПК ЙМЙ ОЕУЛПМШЛЙИ РЕТЕНЕООЩИ ЙМЙ ТБГЙПОБМШОЩЕ ЧЩТБЦЕОЙС. Maple УПДЕТЦЙФ ТБЪМЙЮОЩЕ ЖХОЛГЙЙ ДМС РТЕПВТБЪПЧБОЙС ФБЛЙИ ЧЩТБЦЕОЙК.

жХОЛГЙС factor(eq) ТБЪМБЗБЕФ ЧЩТБЦЕОЙЕ eq ОБ НОПЦЙФЕМЙ.

жХОЛГЙС expand(eq) ТБУЛТЩЧБЕФ УЛПВЛЙ Ч ЧЩТБЦЕОЙЙ. еУМЙ ХЛБЪБФШ ПДЙО ЙМЙ ОЕУЛПМШЛП ДПРПМОЙФЕМШОЩИ РБТБНЕФТПЧ Ч ЧЙДЕ expand(eq,a,b,c) , ФП ЧЩТБЦЕОЙС a , b , c ТБУЛТЩЧБФШУС ОЕ ВХДХФ. ьФП РПМЕЪОП, ЕУМЙ ОЕПВИПДЙНП ЛБЦДПЕ УМБЗБЕНПЕ ХНОПЦЙФШ ОБ ЛБЛПЕ-ФП ЧЩТБЦЕОЙЕ.

дМС РТЙЧЕДЕОЙС ДТПВЕК Л ПВЭЕНХ ЪОБНЕОБФЕМА У РПУМЕДХАЭЙН УПЛТБЭЕОЙЕН ЙУРПМШЪХЕФУС ЖХОЛГЙС normal(eq) .

жХОЛГЙС simplify(eq) ХРТПЭБЕФ ЧЩТБЦЕОЙЕ eq . ч ЛБЮЕУФЧЕ ЧФПТПЗП (ОЕПВСЪБФЕМШОПЗП) РБТБНЕФТБ, ЕК НПЦОП ХЛБЪБФШ, ЛБЛЙЕ ЧЩТБЦЕОЙС РТЕПВТБЪПЧЩЧБФШ: trig – ФТЙЗПОПНЕФТЙЮЕУЛЙЕ, power – УФЕРЕООЩЕ, radical – ТБДЙЛБМЩ, exp – ЬЛУРПОЕОФЩ, ln – МПЗБТЙЖНЩ.

тЕЫЕОЙЕ ХТБЧОЕОЙК

пВЩЛОПЧЕООЩЕ ХТБЧОЕОЙС

дМС ТЕЫЕОЙС ХТБЧОЕОЙК ЙУРПМШЪХЕФУС ЖХОЛГЙС solve(eq,x) , ЗДЕ eq – ТЕЫБЕНПЕ ХТБЧОЕОЙЕ, x – ЙНС РЕТЕНЕООПК, ПФОПУЙФЕМШОП ЛПФПТПК ТБЪТЕЫБЕФУС ХТБЧОЕОЙЕ. рТЙНЕТ:

еУМЙ ХТБЧОЕОЙЕ ЙНЕЕФ ОЕУЛПМШЛП ТЕЫЕОЙК, ФП ТЕЫЕОЙЕ ХТБЧОЕОЙС НПЦОП РТЙУЧПЙФШ ОЕЛПФПТПК РЕТЕНЕООПК, ОБРТЙНЕТ p . дБМЕЕ НПЦОП ЙУРПМШЪПЧБФШ k -Е ТЕЫЕОЙЕ ХТБЧОЕОЙС Ч ЧЙДЕ p[k] :

уЙУФЕНЩ ХТБЧОЕОЙК

уЙУФЕНЩ ХТБЧОЕОЙК ТЕЫБАФУС У РПНПЭША ФБЛПК ЦЕ ЖХОЛГЙЙ solve(,) , ФПМШЛП ФЕРЕТШ Ч РБТБНЕФТБИ ЖХОЛГЙЙ УМЕДХЕФ ХЛБЪЩЧБФШ Ч РЕТЧЩИ ЖЙЗХТОЩИ УЛПВЛБИ ЮЕТЕЪ ЪБРСФХА ХТБЧОЕОЙС, Б ЧП ЧФПТЩИ ЖЙЗХТОЩИ УЛПВЛБИ РЕТЕЮЙУМСАФУС ЮЕТЕЪ ЪБРСФХА РЕТЕНЕООЩЕ, ПФОПУЙФЕМШОП ЛПФПТЩИ ФТЕВХЕФУС ТЕЫЙФШ УЙУФЕНХ. еУМЙ ОЕПВИПДЙНП ЙУРПМШЪПЧБФШ РПМХЮЕООЩЕ ТЕЫЕОЙС ХТБЧОЕОЙК ДМС ДБМШОЕКЫЙИ ЧЩЮЙУМЕОЙК, ФП ОЕПВИПДЙНП ТЕЪХМШФБФ, ЧПЪЧТБЭБЕНЩК ЖХОЛГЙЕК solve РТЙУЧПЙФШ ЛБЛПК-ОЙВХДШ РЕТЕНЕООПК, ОБРТЙНЕТ, p , Б ЪБФЕН ЧЩРПМОЙФШ ЛПНБОДХ assign(p) . рТЙНЕТ:

юЙУМЕООПЕ ТЕЫЕОЙЕ ХТБЧОЕОЙК

рПРТПВХЕН ТЕЫЙФШ ХТБЧОЕОЙЕ: x 6 -2x+1=0. йУРПМШЪПЧБОЙЕ ЖХОЛГЙЙ solve ДБУФ ОБН ПДЙО ЛПТЕОШ -1 Й ЕЭЕ ОБВПТ ЧЩТБЦЕОЙК ЧЙДБ RootOf(_Z^5+_Z^4+_Z^3+_Z^2+_Z-1,index = 1) . дЕМП Ч ФПН, ЮФП РТПЙЪЧПМШОПЕ ХТБЧОЕОЙЕ УФЕРЕОЙ ЧЩЫЕ 4 У ТБГЙПОБМШОЩНЙ ЛПЬЖЖЙГЙЕОФБНЙ НПЦЕФ ОЕ ЙНЕФШ ЛПТОЕК, ЧЩТБЪЙНЩИ Ч ЧЙДЕ ТБДЙЛБМПЧ ОБД ТБГЙПОБМШОЩНЙ ЮЙУМБНЙ. тЕЫЕОЙС ЧУЕЧПЪНПЦОЩИ ФБЛЙИ ХТБЧОЕОЙК ОБЪЩЧБАФУС БМЗЕВТБЙЮЕУЛЙНЙ ЮЙУМБНЙ. дБООПЕ ХТБЧОЕОЙЕ ФБЛЦЕ ОЕТБЪТЕЫЙНП Ч ТБДЙЛБМБИ, Й Maple ОБЫМБ ОБН ЕДЙОУФЧЕООЩК ЛПТЕОШ, ЧЩТБЪЙНЩК Ч ТБДЙЛБМБИ (1) Й УППВЭЙМБ, ЮФП ПУФБЧЫЙЕУС ЛПТОЙ СЧМСАФУС БМЗЕВТБЙЮЕУЛЙНЙ ЮЙУМБНЙ: ЛПТОСНЙ НОПЗПЮМЕОБ z 5 +z 4 +z 3 +z 2 +z-1=0 (ЙНЕООП ЬФПФ НОПЗПЮМЕО ХЛБЪБО Ч БТЗХНЕОФЕ ЖХОЛГЙЙ RootOf ). Maple ХНЕЕФ ТБВПФБФШ У БМЗЕВТБЙЮЕУЛЙНЙ ЮЙУМБНЙ, ОП НПЦОП ФБЛЦЕ ОБКФЙ РТЙВМЙЦЕООПЕ ЮЙУМЕООПЕ ТЕЫЕОЙЕ РТЙ РПНПЭЙ ЖХОЛГЙЙ fsolve :

йОПЗДБ Maple РТЙ ТЕЫЕОЙЙ ФТБОУГЕОДЕОФОЩИ ХТБЧОЕОЙК ОЕ ЧЩЧПДЙФ УМПЦОЩЕ ЧЩТБЦЕОЙС Ч ЧЙДЕ ТБДЙЛБМПЧ, Б ПУФБЧМСЕФ ЙИ Ч ЖПТНЕ RootOf. юФПВЩ ЪБУФБЧЙФШ Maple ЧЩЧПДЙФШ ЧУЕ ТЕЫЕОЙС Ч ЧЙДЕ ТБДЙЛБМПЧ (ЕУФЕУФЧЕООП, ЕУМЙ ПОЙ РТЕДУФБЧЙНЩ Ч ФБЛПК ЖПТНЕ), ОЕПВИПДЙНП РТЙУЧПЙФШ ЪОБЮЕОЙЕ true УЙУФЕНОПК РЕТЕНЕООПК _EnvExplicit ( _EnvExplicit:=true ).

тЕЫЕОЙЕ ФТЙЗПОПНЕФТЙЮЕУЛЙИ ХТБЧОЕОЙК

лПНБОДБ solve , РТЙНЕОСЕНБС ДМС ТЕЫЕОЙС ФТЙЗПОПНЕФТЙЮЕУЛЙИ ХТБЧОЕОЙК, ОБИПДЙФ ФПМШЛП ЗМБЧОЩЕ ТЕЫЕОЙС, ФП ЕУФШ ЧЩЧПДЙФ ФПМШЛП ПДОП ТЕЫЕОЙЕ ЙЪ УЕТЙЙ РЕТЙПДЙЮЕУЛЙИ ТЕЫЕОЙК:

дМС ФПЗП, ЮФПВЩ Maple ОБИПДЙМБ ЧУЕ ТЕЫЕОЙС, ОЕПВИПДЙНП РТЕДЧБТЙФЕМШОП РТЙУЧПЙФШ ЪОБЮЕОЙЕ true УЙУФЕНОПК РЕТЕНЕООПК _EnvAllSolutions . фПЗДБ НЩ РПМХЮЙН ТЕЪХМШФБФ Ч ДТХЗПН ЧЙДЕ, Ч ЛПФПТПН ВХДХФ ЖЙЗХТЙТПЧБФШ РЕТЕНЕООЩЕ Z1

. ьФЙ РЕТЕНЕООЩЕ ПВПЪОБЮБАФ РТПЙЪЧПМШОХА ЛПОУФБОФХ ГЕМПЗП ФЙРБ, Ч ВПМЕЕ РТЙЧЩЮОПН ЧЙДЕ ТЕЫЕОЙС НПЦОП ВХДЕФ ЪБРЙУБФШ, ЛБЛ π/4+πn , πk .