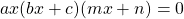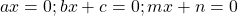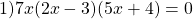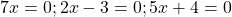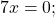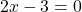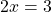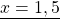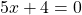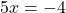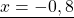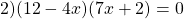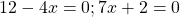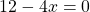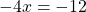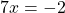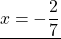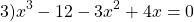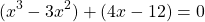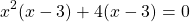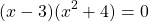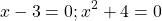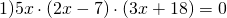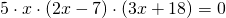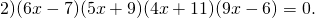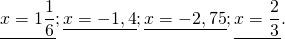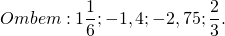Что такое «уравнения равные нулю»?
Если в левой части уравнения стоит сумма или разность одночленов или многочленов, а в правой части — нуль, то это может быть обычное линейное уравнение.
Если левая часть уравнения представляет собой произведения двух или нескольких множителей, а правая часть — нуль, то это — уравнение типа «произведение равно нулю».
В общем виде простейшие равные нулю уравнения можно записать как
(множителей может быть больше).
Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому приравниваем к нулю каждый множитель:
и решаем каждое из полученных уравнений отдельно.
Это — уравнение типа «произведение равно нулю».
Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
Если в уравнении, равном 0, левую часть можно разложить на множители, то такое уравнение также можно решить как уравнение типа «произведение равно 0».
Сгруппируем первое слагаемое с третьим, а четвёртое — со вторым:
Из первых скобок вынесем за скобки общий множитель x², из вторых — 4:
Общий множитель (x-3) вынесем за скобки:
Получили уравнение типа «произведение равно 0». Приравниваем к нулю каждый из множителей:
Корень первого уравнения —
Второе уравнение не имеет корней (сумма положительных чисел не может равняться нулю).
В алгебре многие уравнения сводятся к уравнениям типа «произведение равно нулю» с помощью разложения на множители.
Множители могут линейными, квадратными, логарифмическими, тригонометрическими и т.д. уравнениями.
Еще один важный частный случай уравнений, равных нулю, рассмотрим позже.
13 комментариев
Показательное уравнение:
3^((x+2)/(3x-4))-2*3^((5x-10)/(3x-4))-7=0
Корень известен: x=2.
Подскажите, пожалуйста, как найти решение. Преобразовать в квадратное уравнение что-то не получается.
Видео:Как решать уравнение со скобками Уравнение вида произведение элементов=0 Произведение скобок=0Скачать

Произведение равно нулю
В каком случае произведение равно нулю?
произведение равно нулю, если хотя бы один из множителей равен нулю .
С помощью этого правила решают уравнения, в которых произведение нескольких множителей равно нулю. Уравнения вида «Произведение равно нулю» — одни из самых распространенных в математике. Их начинают изучать с 6 класса. В 6 классе множители представляют собой линейные уравнения.
Это уравнение вида «произведение равно нулю». Произведение равно нулю, если хотя бы один из множителей равен нулю, поэтому приравниваем к нулю каждый из множителей:
5x=0 или 2x-7=0 или 3x+18=0.
Теперь решаем каждое из уравнений. Первое — простейшее линейное уравнение. Обе части уравнения делим на число, стоящее перед иксом:
Второе и третье — линейные уравнения. Алгоритм решения: неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
2x=7 I :2 3x=-18 I :3
Замечания.
1) Это уравнение также можно рассмотреть как произведение четырех множителей:
Рассуждаем так: поскольку произведение равно нулю, если хотя бы один из множителей равен нулю, а первый множитель 5≠0, приравниваем к нулю остальные множители:
x=0 или 2x-7=0 или 3x+18=0.
2) Поскольку перед буквой и перед скобками знак умножения можно не писать, условие уравнений обычно выглядят так:
Это уравнение типа «произведение равно нулю». Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
6x-7=o или 5x+9=0 или 4x+11=0 или 9x-6=0
6x=7 I:6 5x=-9 I:5 4x=-11 I:4 9x=6 I:9
x=7/6 x=-9/5 x=-11/4 x=6/9
В первом уравнении получили неправильную дробь. Выделяем из нее целую часть. Во втором и третьем уравнении ответ записываем в виде десятичной дроби. Для этого делим числитель на знаменатель уголком. В четвертом уравнении нужно сократить дробь в ответе
А как узнать, записать ответ в виде обыкновенной или в виде десятичной дроби? Любую ли обыкновенную дробь можно перевести в десятичную? Любую ли десятичную дробь можно перевести в обыкновенную? Об этом мы поговорим в следующий раз.
Видео:ОГЭ Задание 21 Когда произведение равно нулюСкачать

2 Comments
определение наверху неверное, т.к. произведение двух или более множителей равно нулю тогда и только тогда когда хотя-бы один из них равен нулю, а остальные не теряют смысла.
Мне понравился ход мысли Вашего учителя математики. Она расширила определение, чтобы ученики не забывали проверить, входят ли найденные корни в область допустимых значений уравнения (или неравенства).
Видео:Уравнение в котором произведение множителей равно нулю. Алгебра 7 класс.Скачать

В помощь школьнику
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Уравнение произведение равно нулю. Если один из множителей равен нулю, то произведение равно нулю
Если один и двух множителей равен 1, то произведение равно другому множителю.
III. Работа над новым материалом.
Объяснить прием умножения для случаев, когда в середине записи многозначного числа есть нули, ученики могут сами: например, учитель предлагает вычислить произведение чисел 907 и 3. Ученики записывают решение в столбик, рассуждая: «Пишу число 3 под единицами.
Умножаю на 3 число единиц: трижды семь – 21, это 2 дес. и 1 ед.; пишу 1 под единицами, а 2 дес. запоминаю. Умножаю десятки: 0 умножить на 3, получится 0, да ещё 2, получится 2 десятка, пишу 2 под десятками. Умножаю сотни: 9 умножить на 3, получится 27, пишу 27. Читаю ответ: 2 721».
Для закрепления материала ученики решают примеры из задания 361 с подробным объяснением. Если учитель видит, что дети разобрались с новым материалом хорошо, то он может предложить краткое комментирование.
Учитель. Будем объяснять решение кратко, называть только число единиц каждого разряда первого множителя, которые умножаете, и результат, не называя какого разряда эти единицы. Умножим 4 019 на 7. Объясняю: 9 умножу на 7, получу 63, 3 пишу, 6 запоминаю. 1 умножаю на 7, получается 7, да еще 6 – это 13, 3 пишу, 1 запоминаю. Ноль умножить на 7, получается ноль, да ещё 1, получу 1, пишу 1. 4 умножу на 7, получу 28, пишу 28. Читаю ответ: 28 133.
Ф и з к у л ь т м и н у т к а
IV. Работа над пройденным материалом.
1. Решение задач.
Задачу 363 учащиеся решают с комментированием. После чтения задачи записывается краткое условие.
Учитель может предложить учащимся решить задачу двумя способами.
О т в е т: 7 245 ц зерна убрал всего.
Задачу 364 дети решают самостоятельно (с последующей проверкой).
1) 42 · 10 = 420 (ц) – пшеницы
2) 420: 3 = 140 (ц) – ячменя
3) 420 – 140 = 280 (ц)
О т в е т: на 280 ц пшеницы больше.
2. Решение примеров.
Задание 365 дети выполняют самостоятельно: записывают выражения и находят их значения.
Учитель. Ребята, что нового узнали на уроке?
Дети. Мы познакомились с новым приемом умножения.
Учитель. Что повторяли на уроке?
Дети. Решали задачи, составляли выражения и находили их значения.
Домашнее задание: задания 362, 368; тетрадь № 1, с. 52, № 5–8.
У р о к 58
Умножение чисел, запись которых
оканчивается нулями
Цели: познакомить с приемом умножения на однозначное число многозначных чисел, оканчивающихся одним или несколькими нулями; закрепить умение решать задачи, примеры на деление с остатком; повторить таблицу единиц времени.
Как по внешнему виду уравнения определить, будет ли это уравнение неполным квадратным уравнением? А как решать неполные квадратные уравнения?
Как узнать «в лицо» неполное квадратное уравнение
Левая часть уравнения есть квадратный трёхчлен , а правая — число 0. Такие уравнения называют полными квадратными уравнениями.
У полного квадратного уравнения все коэффициенты , и не равны 0. Для их решения существуют специальные формулы, с которыми мы познакомимся позднее.
Наиболее простыми для решения являются неполные квадратные уравнения. Это такие квадратные уравнения, в которых некоторые коэффициенты равны нулю .
Коэффициент по определению не может быть равным нулю , так как иначе уравнение не будет квадратным. Об этом мы говорили. Значит, получается, что обратиться в нуль могут только коэффициенты или .
В зависимости от этого существует три вида неполных квадратных уравнений.
1) 

2) 

3) , где 
Итак, если мы видим квадратное уравнение, в левой части которого вместо трёх членов присутствуют два члена или один член , то такое уравнение будет неполным квадратным уравнением.
Определение неполного квадратного уравнения
Неполным квадратным уравнением называется такое квадратное уравнение , в котором хотя бы один из коэффициентов или равен нулю .
В этом определении есть очень важное словосочетание «хотя бы один из коэффициентов … равен нулю «. Это значит, что один или больше коэффициентов могут равняться нулю .
Исходя из этого возможны три варианта : или один коэффициент равен нулю, или другой коэффициент равен нулю, или оба коэффициента одновременно равны нулю. Вот так и получаются три вида неполного квадратного уравнения.
Неполными квадратными уравнениями являются такие уравнения:
1)
2)
3)
Решение уравнения 
Наметим план решения этого уравнения. Левую часть уравнения можно легко разложить на множители , так как в левой части уравнения у членов и есть общий множитель , его можно вынести за скобку. Тогда слева получится произведение двух множителей, а справа — нуль.
А затем будет работать правило «произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл» . Всё очень просто!
Итак, план решения .
1) Левую часть раскладываем на множители.
2) Пользуемся правилом «произведение равно нулю…»
Уравнения подобного типа я называю «подарок судьбы» . Это такие уравнения, у которых правая часть равна нулю , а левую часть можно разложить на множители .
Решаем уравнение 
1) Разложим левую часть уравнения на множители , для этого вынесем общий множитель , получим такое уравнение .
2) В уравнении мы видим, что слева стоит произведение , а справа нуль .
Настоящий подарок судьбы! Здесь мы, конечно, воспользуемся правилом «произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл «.
При переводе этого правила на язык математики получим два уравнения или .
Мы видим, что уравнение распалось на два более простых уравнения, первое из которых уже решено ().
Решим второе уравнение . Перенесём неизвестные члены влево, а известные вправо. Неизвестный член уже стоит слева, мы его там и оставим. А известный член перенесём вправо с противоположным знаком. Получим уравнение .
Мы нашли , а нам надо найти . Чтобы избавиться от множителя , надо обе части уравнения разделить на .
«Параллельность двух прямых» — Доказать, что AB || CD. C – секущая для а и b. ВС – биссектриса угла ABD. Будут ли m || n? Примеры параллельностей в реальной жизни. Параллельны ли прямые? Назовите пары: — накрест лежащих углов; — соответственных углов; — односторонних углов; Первый признак параллельности прямых. Доказать, что АС || BD.
«Два мороза» — Ну, думаю, погоди у меня теперь. Два мороза. А к вечеру встретились опять в чистом поле. Покачал головой Мороз — Синий нос и говорит: — Э, молод ты, брат, и глуп. Пусть, как оденется, да узнает, каков Мороз — Красный нос. Поживи с моё, так узнаешь, что топор лучше шубы греет. Ну, думаю, доберёмся до места, тут я тебя и прихвачу.
«Линейное уравнение с двумя переменными» — Определение: Линейное уравнение с двумя переменными. Алгоритм доказательства, что данная пара чисел является решением уравнения: Приведите примеры. -Какое уравнение с двумя переменными называется линейным? -Что называется уравнением с двумя переменными? Равенство, содержащее две переменные, называется уравнением с двумя переменными.
«Интерференция двух волн» — Интерференция. Причина? Опыт Томаса Юнга. Интерференция механических волн на воде. Длина волны. Интерференция света. Устойчивая интерференционная картина наблюдается при условии когерентности налагающихся волн. Радиотелескоп-интерферометр, расположенный в Нью-Мексико, США. Применение интерференции. Интерференция механических волн звука.
«Признак перпендикулярности двух плоскостей» — Упражнение 6. Перпендикулярность плоскостей. Ответ: Да. Существует ли треугольная пирамида, у которой три грани попарно перпендикулярны? Упражнение 1. Найдите углы ADB и ACB. Ответ: 90о, 60о. Упражнение 10. Упражнение 3. Упражнение 7. Упражнение 9. Верно ли, что две плоскости, перпендикулярные третьей, параллельны?
«Неравенства с двумя переменными» — Геометрической моделью решений неравенства является средняя область. Цель урока: Решения неравенств с двумя переменными. 1.Построить график уравнения f(х, у) = 0 . Для решения неравенств с двумя переменными используется графический метод. Окружности разбили плоскость на три области. Неравенство с двумя переменными чаще всего имеет бесконечное множество решений.
🔥 Видео
Как решать дробно-рациональные уравнения? | МатематикаСкачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

Уравнения. Когда произведение равно нулю. ОГЭ.Скачать

ОГЭ для НОЛИКОВ, Уравнения N-9Скачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Дробно-рациональные уравнения. 8 класс.Скачать

Решение матричных уравненийСкачать

ТЕОРЕМА ВИЕТА ЗА 2 МИНУТЫСкачать

07. Решение уравнения, вынесением за скобки общего множителяСкачать

Уравнения Когда произведение равно нулю.Скачать

Неполное квадратное уравнение (с=0). Алгебра 8 класс. Произведение равно нулю.Скачать

Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Сложные уравнения. Как решить сложное уравнение?Скачать

Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

М7 (30.1-30.18) Разложение на множители. Когда произведение равно нулю?Скачать