Решение уравнения описывающего свободные колебания (7 видео)

Содержание

Свободные колебания.
Механические колебания.
Гармонические колебания.
Уравнение гармонических колебаний.
Пружинный маятник.
Математический маятник.
Свободные и вынужденные колебания.
Колебательное движение. Свободные колебания. Колебательные системы (Ерюткин Е.С.)
🎥 Видео

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Свободные колебания.

Свободные колебания (или собственные колебания) — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии (потенциальной или кинетической) при отсутствии внешних воздействий.

Потенциальная или кинетическая энергия может быть сообщена, например, в механических системах через начальное смещение или начальную скорость.

Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними образуют систему тел, которая называется колебательной системой.

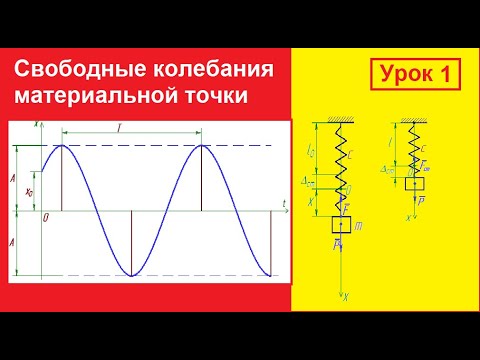
Например, пружина, шарик и вертикальная стойка, к которой прикреплен верхний конец пружины (см. рис. ниже), входят в колебательную систему. Здесь шарик свободно скользит по струне (силы трения пренебрежимо малы). Если отвести шарик вправо и предоставить его самому себе, он будет совершать свободные колебания около положения равновесия (точки О) вследствие действия силы упругости пружины, направленной к положению равновесия.

Другим классическим примером механической колебательной системы является математический маятник (см. рис. ниже). В данном случае шарик совершает свободные колебания под действием двух сил: силы тяжести и силы упругости нити (в колебательную систему входит также Земля). Их равнодействующая направлена к положению равновесия.

Силы, действующие между телами колебательной системы, называются внутренними силами. Внешними силами называются силы, действующие на систему со стороны тел, не входящих в нее. С этой точки зрения свободные колебания можно определить как колебания в системе под действием внутренних сил после того, как система выведена из положения равновесия.

Условиями возникновения свободных колебаний являются:

1) возникновение в них силы, возвращающей систему в положение устойчивого равновесия, после того как ее вывели из этого состояния;

2) отсутствие трения в системе.

Динамика свободных колебаний.

Колебания тела под действием сил упругости. Уравнение колебательного движения тела под действием силы упругости F (см. рис.) может быть получено с учетом второго закона Ньютона (F = mа) и закона Гука (F_упр = -kx), где m — масса шарика, а — ускорение, приобретаемое шариком под действием силы упругости, k — коэффициент жесткости пружины, х — смещение тела от положения равновесия (оба уравнения записаны в проекции на горизонтальную ось Ох). Приравнивая правые части этих уравнений и учитывая, что ускорение а — это вторая производная от координаты х (смещения), получим:

Это дифференциальное уравнение движения тела, колеблющегося под действием силы упругости: вторая производная координаты по времени (ускорение тела) прямо пропорциональна его координате, взятой с противоположным знаком.

Колебания математического маятника. Для получения уравнения колебания математического маятника (рисунок) необходимо разложить силу тяжести F_T = mg на нормальную F_n (направленную вдоль нити) и тангенциальную F_τ (касательную к траектории движения шарика — окружности) составляющие. Нормальная составляющая силы тяжести F_n и сила упругости нити F_ynp в сумме сообщают маятнику центростремительное ускорение, не влияющее на величину скорости, а лишь меняющее ее направление, а тангенциальная составляющая F_τ является той силой, которая возвращает шарик в положение равновесия и заставляет его совершать колебательные движения. Используя, как и в предыдущем случае, закон Ньютона для тангенциального ускорения ma_τ = F_τ и учитывая, что F_τ = -mg sinα, получим:

Знак минус появился потому, что сила и угол отклонения от положения равновесия α имеют противоположные знаки. Для малых углов отклонения sin α ≈ α. В свою очередь, α = s/l, где s — дуга OA, I — длина нити. Учитывая, что а_τ = s», окончательно получим:

Вид уравнения аналогичен уравнению . Только здесь параметрами системы являются длина нити и ускорение свободного падения, а не жесткость пружины и масса шарика; роль координаты играет длина дуги (т. е. пройденный путь, как и в первом случае).

Таким образом, свободные колебания описываются уравнениями одного вида (подчиняются одним и тем же законам) независимо от физической природы сил, вызывающих эти колебания.

Решением уравнений и является функция вида:

То есть координата тела, совершающего свободные колебания, меняется с течением времени по закону косинуса или синуса, и, следовательно, эти колебания являются гармоническими:

В уравнении x = x_m cos ω₀ t (или x = x_m sin ω₀ t), х_m — амплитуда колебания, ω₀ — собственная циклическая (круговая) частота колебаний.

Циклическая частота и период свободных гармонических колебаний определяются свойствами системы. Так, для колебаний тела, прикрепленного к пружине, справедливы соотношения:

Собственная частота тем больше, чем больше жесткость пружины или меньше масса груза, что вполне подтверждается опытом.

Для математического маятника выполняются равенства:

Эта формула была впервые получена и проверена на опыте голландским ученым Гюйгенсом (современником Ньютона).

Период колебаний возрастает с увеличением длины маятника и не зависит от его массы.

Следует особо обратить внимание на то, что гармонические колебания являются строго периодическими (т. к. подчиняются закону синуса или косинуса) и даже для математического маятника, являющегося идеализацией реального (физического) маятника, возможны только при малых углах колебания. Если углы отклонения велики, смещение груза не будет пропорционально углу отклонения (синусу угла) и ускорение не будет пропорционально смещению.

Скорость и ускорение тела, совершающего свободные колебания, также будут совершать гармонические колебания. Беря производную по времени функции (x = x_m cos ω₀ t (или x = x_m sin ω₀ t)), получим выражение для скорости:

где a_m = ω 2 ₀ x_m — амплитуда ускорения. Таким образом, амплитуда скорости гармонических колебаний пропорциональна частоте, а амплитуда ускорения — квадрату частоты колебания.

Видео:Урок 343. Затухающие колебания (часть 1)Скачать

Механические колебания.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.

Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.

Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.

Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.

Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.

Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.

Частота колебаний — это величина, обратная периоду: . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Гармонические колебания.

Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение . Основная задача механики в данном случае состоит в нахождении функции , дающей координату тела в любой момент времени.

Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.

Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.

Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:

Выясним смысл входящих в эту формулу величин.

Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому — амплитуда колебаний.

Аргумент косинуса называется фазой колебаний. Величина , равная значению фазы при , называется начальной фазой. Начальная фаза отвечает начальной координате тела: .

Величина называется циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное радиан: , откуда

Измеряется циклическая частота в рад/с (радиан в секунду).

В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1) :

График функции (1) , выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1 .

Решение уравнения описывающего свободные колебания

Рис. 1. График гармонических колебаний

Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.

Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить . Мы получаем закон косинуса:

График гармонических колебаний в этом случае представлен на рис. 2 .

Рис. 2. Закон косинуса

Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить . Получаем закон синуса:

График колебаний представлен на рис. 3 .

Рис. 3. Закон синуса

Видео:Физика 11 класс (Урок№7 - Свободные и вынужденные электромагнитные колебания. Колебательный контур.)Скачать

Уравнение гармонических колебаний.

Вернёмся к общему гармоническому закону (1) . Дифференцируем это равенство:

Теперь дифференцируем полученное равенство (4) :

Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :

Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:

C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:

-решением уравнения (7) является всякая функция вида (1) с произвольными ;

-никакая другая функция решением данного уравнения не является.

Иными словами, соотношения (6) , (7) описывают гармонические колебания с циклической частотой и только их. Две константы определяются из начальных условий — по начальным значениям координаты и скорости.

Видео:5.4 Уравнение гармонических колебанийСкачать

Пружинный маятник.

Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4 ). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .

Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рис. 4. Пружинный маятник

В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:

Если 0′ alt=’x>0′ /> (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и . Наоборот, если , то 0′ alt=’F_>0′ /> . Знаки и всё время противоположны, поэтому закон Гука можно записать так:

Тогда соотношение (8) принимает вид:

Мы получили уравнение гармонических колебаний вида (6) , в котором

Циклическая частота колебаний пружинного маятника, таким образом, равна:

Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:

Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10) .

Видео:Колебательное движение. Свободные колебания | Физика 9 класс #23 | ИнфоурокСкачать

Математический маятник.

Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5 ). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

Рис. 5. Математический маятник

Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.

Запишем для маятника второй закон Ньютона:

и спроектируем его на ось :

Если маятник занимает положение как на рисунке (т. е. 0′ alt=’x>0′ /> ), то:

Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:

Итак, при любом положении маятника имеем:

Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11) :

Это — уравнение гармонических колебаний вида (6) , в котором

Следовательно, циклическая частота колебаний математического маятника равна:

Отсюда период колебаний математического маятника:

Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.

Видео:Свободные электромагнитные колебания. 11 класс.Скачать

Свободные и вынужденные колебания.

Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6 ).

Рис. 6. Затухающие колебания

Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).

Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:

В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7 .

Рис. 7. Резонанс

Мы видим, что вблизи частоты наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, , а амплитуда колебаний возрастает до бесконечности при .

Видео:Урок 327. Гармонические колебанияСкачать

Колебательное движение. Свободные колебания. Колебательные системы (Ерюткин Е.С.)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Тема данного урока: «Колебательное движение. Свободные колебания. Колебательные системы». Вначале дадим определение нового вида движения, который мы начинаем изучать, – колебательного движения. Рассмотрим в качестве примера колебания пружинного маятника и определим понятие свободных колебаний. Также изучим, что такое колебательные системы, и обсудим условия, необходимые для существования колебаний.