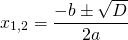Решение уравнения на си шарп (4 видео)

Программирование на C, C# и Java

Содержание

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
Решение квадратного уравнения на С# в Windows Forms.
Решение квадратного уравнения
Решение уравнений методом касательных (алгоритм Ньютона) на C#
📹 Видео

Видео:Решение квадратного уравнения на C# для консоли Windows в Visual Studio 2022Скачать

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode

Видео:ОПЕРАТОРЫ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ С ЧИСЛАМИ В C# | C# ОТ НОВИЧКА К ПРОФЕССИОНАЛУ | Урок # 8Скачать

Решение квадратного уравнения на С# в Windows Forms.

Сегодня мы напишем программу, которая выведет нам решение квадратного уравнения на С#. Сделаем мы всё это в Windows Forms. В программе мы найдём дискриминант и оба корня.

Для создания программы нам понадобится знание начальной школы и трёх формул.

Формула нахождения дискриминанта:

Формула нахождения корней выражения, если дискриминант больше нуля:

И формула нахождения одного корня выражения, если дискриминант равен нулю:

Ну и, пожалуй, стоит вспомнить сам вид квадратного выражения:

Теперь пора приступать к программе.

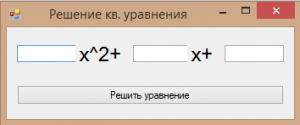
Для начала создаём незамысловатую форму под наши нужды:

Здесь у нас 3 TextBox’a, 2 Label’a и 1 кнопка Button. Выводить решение мы будем в отдельном MessageBox’е.

Приступаем к коду. Дважды щёлкаем на Button и в открывшемся участке кода начинаем писать.

Сначала объявляем переменные, которым будут присвоены значения,введённые пользователем в TextBox’ы:

Видео:Решение уравнений (метод дихотомии) на C#Скачать

Решение квадратного уравнения

Уравнение вида a⋅x 2 + b⋅x + c = 0 — квадратное уравнение.

a, b, c — действительные числа, a ≠ 0.

Для того чтобы вычислить корни квадратного уравнения, нужно сначала найти дискриминант.

D = b 2 — 4⋅a⋅c;

если D 0, то уравнение имеет два действительных корня:
- x₁ = (-b + √D) / (2⋅a);
- x₂ = (-b + √D) / (2⋅a).

Видео:C# ФУНКЦИИ И МЕТОДЫ | МЕТОД C# ЧТО ЭТО | ФУНКЦИИ C# ПРИМЕР | C# ОТ НОВИЧКА К ПРОФЕССИОНАЛУ | # 35Скачать

Решение уравнений методом касательных (алгоритм Ньютона) на C#

Привет! Сегодня посмотрим, как приближённо решать уравнения с помощью метода касательных (алгоритма Ньютона).

И напишем программу на языке программирования C#.

Пусть дано нелинейное уравнение: f(x) = 0 (Если уравнение будет линейное, то невозможно будет провести касательную). Метод касательных поможет приближённо найти корень уравнения на отрезке [a, b], при условии, что функция непрерывна на замкнутом интервале [a, b], и корень на этом отрезке только один! А так же функция не меняет свою вогнутость или выпуклость (постоянный знак второй производной) и не имеет экстремумов (первая производная не равна нулю) на отрезке [a, b].

Графически функция может выглядеть следующим образом:

Т.е. самая стандартная функция.

Графическая интерпретация метода Ньютона:

От x₀ узнаём значение функции. В этой точке проводим касательную. Касательная пересекает ось X, и мы получаем новую точку x₁. И начинаем всё сначала. Числа x₀, x₁, x₂ и т.д. приближаются к корню уравнения.

Выведем формулу для x_n.

Приравняем к нулю (пересечение с осью X) и выразим x.

Погрешность данного метода ε > |x_n+1 — x_n|. Причём самая первая точка x₀ не берётся во внимание при определении погрешности. Т.е. если |x_n+1 — x_n| меньше, чем заданное значение ε, то можно прекращать вычисления.

За саму первую точку x₀ берут либо начало отрезка a, либо конец отрезка b. Это зависит от возрастания или убывания функции, а так же, в какую сторону выпукла функция.

Удобно пользоваться правилом:

Для примера, найдём положительный корень уравнения: x 2 = 2

Определим отрезок [1, 2], где будем искать корень.

Функция f(x) = x 2 — 2

f′′(x) = 2
f(2) = 4 — 2 = 2

Определим корень уравнения с точностью до ε=0.001 на языке программирования C#.

Т.к. x₀ — не участвует при вычислении погрешности, то мы в начале до цикла while вычисляем x_n и x_n+1 (xnp1). Т.к. тип данных double, то чтобы возвести число в степень, используем специальную функцию Math.Pow(). В условии цикла while мы используем разницу без модуля, потому что мы идём от правого конца отрезка, и xn всегда больше, чем xnp1.