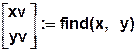Решение уравнения методом простой итерации матлаб (8 видео)

Решение нелинейных уравнений в Matlab

Доброго времени суток. В этой статье мы разберем решение простых нелинейных уравнений с помощью средств Matlab. Посмотрим в действии как стандартные функции, так и сами запрограммируем три распространенных метода для решения нелинейных уравнений.

Содержание

Общая информация
Стандартные функции Matlab
Метод перебора Matlab
Метод простых итераций Matlab
Метод половинного деления Matlab
Заключение
Программная реализация метода простой итерации для решения СЛАУ в пакете MATLAB
💡 Видео

Общая информация

Уравнения, которые содержат переменные, находящиеся в степенях, отличающихся от единицы, или имеющие нелинейные математические выражения (корень, экспонента, логарифм, синус, косинус и т.д.), а также имеющие вид f(x) = 0 называются нелинейными. В зависимости от сложности такого уравнения применяют методы для решения нелинейных уравнений.

В этой статье, помимо стандартных функций Matlab, мы рассмотрим следующие методы:

Метод перебора
Метод простых итераций
Метод половинного деления

Рассмотрим коротко их алгоритмы и применим для решения конкретной задачи.

Стандартные функции Matlab

Для решения нелинейных уравнений в Matlab есть функция fzero. Она принимает в качестве аргументов саму функцию, которую решаем, и отрезок, на котором происходит поиск корней нелинейного уравнения.

И сразу же разберем пример:

Решить нелинейное уравнение x = exp(-x), предварительно определив интервалы, на которых существуют решения уравнения.

Итак, для начала следует привести уравнение к нужному виду: x — exp(-x) = 0 , а затем определить интервалы, в которых будем искать решение уравнения. Методов для определения интервалов множество, но так как пример достаточно прост мы воспользуемся графическим методом.

Здесь задали примерные границы по оси x, чтобы можно было построить график и посмотреть как ведет себя функция. Вот график:

Из графика видно, что на отрезке [0;1] есть корень уравнения (там, где y = 0), соответственно в дальнейшем будем использовать этот интервал. Чем точнее выбран интервал, тем быстрее метод придет к решению уравнения, а для сложных уравнений правильный выбор интервала определяет погрешность, с которой будет получен ответ.

С помощью стандартной функции Matlab находим корень нелинейного уравнения и выводим. Теперь для проверки отобразим все это графически:

Как вы видите, все достаточно точно просчиталось. Теперь мы исследуем эту же функцию с помощью других методов и сравним полученные результаты.

Метод перебора Matlab

Видео:Метод простой итерации Пример РешенияСкачать

Самый простой метод, который заключается в том, что сначала задается какое то приближение x (желательно слева от предполагаемого корня) и значение шага h. Затем, пока выполняется условие f(x) * f(x + h) > 0, значение x увеличивается на значение шага x = x + h. Как только условие перестало выполняться — это значит, что решение нелинейного уравнения находится на интервале [x; x + h].

Теперь реализуем метод перебора в Matlab:

Лучше всего создать новый m-файл, в котором и прописать код. После вызова получаем такой вывод:

Функцию объявляем с помощью очень полезной команды inline, в цикле пока выполняется условие отсутствия корней (или их четного количества), прибавляем к x значение шага. Очевидно, что чем точнее начальное приближение, тем меньше итераций необходимо затратить.

Метод простых итераций Matlab

Этот метод заключается в том, что функцию преобразуют к виду: x = g(x). Эти преобразования можно сделать разными способами, в зависимости от вида начальной функции. Помимо этого следует задать интервал, в котором и будет производиться итерационный процесс, а также начальное приближение. Сам процесс строится по схеме x_n= g(x_n-1). То есть итерационно проходим от предыдущего значения к последующему.

Процесс заканчивается как только выполнится условие: , то есть, как только будет достигнута заданная точность. И сразу же разберем реализацию метода простых итераций в Matlab для примера, который был приведен выше.

Здесь должно быть все понятно, кроме одного: зачем задавать число итераций? Это нужно для того, чтобы программа не зацикливалась и не выполняла ненужные итерации, а также потому что не всегда программа может просчитать решение с нужной точностью — поэтому следует ограничивать число итераций.

А вот и вывод программы:

Очевидно, что метод простых итераций работает гораздо быстрее и получает точное решение.

Метод половинного деления Matlab

Метод достаточно прост: существует отрезок поиска решения [a;b], сначала находят значение функции в точке середины c, где c = (a+b)/2. Затем сравнивают знаки f(a) и f(c). Если знаки разные — то решение находится на отрезке [a;c], если нет — то решение находится на отрезке [c;b]. Таким образом мы сократили область в 2 раза. Такое сокращение происходит и дальше, пока не достигнем заданной точности.

Перейдем к реализации метода в Matlab:

Все самое важное происходит в цикле: последовательно сокращаем область нахождения решения, пока не будет достигнута заданная точность.
Вот что получилось в выводе:

Этот метод хорошо работает, когда правильно определен интервал, на котором находится решение. Тем не менее, метод простых итераций считается наиболее точным и быстрым.

Заключение

Сегодня мы рассмотрели решение нелинейных уравнений в Matlab. Теперь нам известны методы перебора, половинного деления, простых итераций. А также, когда нам не важно реализация метода, то можно использовать стандартную функцию в Matlab.

Видео:Алгоритмы С#. Метод простых итерацийСкачать

На этом все — спасибо за внимание. В следующей статье мы разберем решение систем нелинейных уравнений в matlab.

Программная реализация метода простой итерации для решения СЛАУ в пакете MATLAB

Входные параметры: U – расширенная матрица коэффициентов, eps – требуемая точность решения.

Function res = Jakobi(U,eps);

error (‘Неверно задана система’);

%приведение системы к диагонально доминирующему виду

error(‘Система не совместна’);

%сумма по строкам

if k 1) && (max_norm2>1) && (max_norm3>1))

error(‘Введенная матрица не является диагонально преобладающей’)

%нахождение суммы для Х1(i)

sum = sum + ( A(i,j) * X0(j) );

while ( abs( X0(i) — X1(i) ) > eps )

%нахождение суммы для Х1(i)

Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

sum = sum + ( A(i,j) * X0(j) );

%вывод вектора решений

%вывод числа итераций для выполненияусловия точности

ВСТРОЕННЫЕ ФУНКЦИИ ПАКЕТОВ MATHCAD И MATLAB

ДЛЯ ПРИБЛИЖЕННОГО РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ

АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Пакет MATHCAD

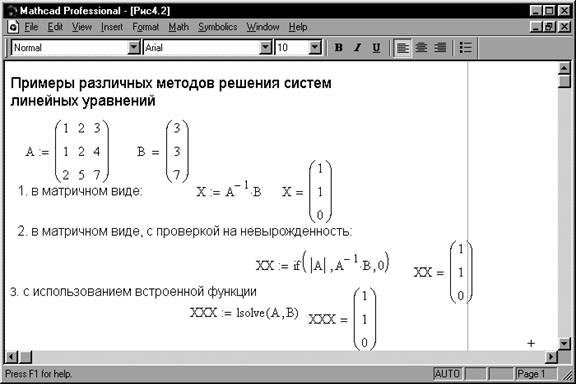
Решение систем линейных уравнений – довольно распространенная задача. Для системы линейных уравнений, заданной в матричном виде AX=B, вектор решения можно получить из очевидного выражения X=A-1B, или, например, из решения системы уравнений с проверкой на невырожденность матрицы:X:=if(|A|,A -1 B,0).

Следует обратить внимание на то, что пакет содержит и встроенную функцию решения линейных систем lsolve(A,B), где А– матрица коэффициентов, а В – вектор свободных членов. Пример использования предложенных методов показан на рис. 5.1.

Рис. 5.1. Примеры решения системы

Для решения систем уравнений, систем неравенств, смешанных систем служат решающие блоки. Структура решающего блока:

начало | Given

тело | несколько конструкций вида АВ1 оп АВ2

Видео:Метод итерацийСкачать

(оп – некоторая операция отношения, причём для написания знака равенства используется особый «жирный» знак равенства, который находится на панели инструментов; знак присваивания в теле решающего блока не используется)

конец | FIND (список) или MINERR (список).

Список – это перечень переменных, которые необходимо найти.

С помощью FIND ищут точное решение; если оно отсутствует, то возникает ошибка. Посредством MINERR всегда будет найдено решение, минимизирующее невязку ограничений. Переменная ERR– величина ошибки.

Перед решающим блоком необходимо задать начальные условия для всех искомых переменных, можно в векторном виде. Соответственно, в теле решающего блока можно использовать запись уравнений в матричном виде. Максимальное количество уравнений в системе доведено до двухсот. Часто приходится решать системы уравнений при наличии определенных ограничений. Таким образом, в теле решающего блока могут быть одновременно как равенства, так и неравенства. Пример такой системы приведен ниже:

Given

find (x,y) =

Для последующего использования результатов необходимо так организовать конец:

В теле решающего блока нельзя строить графики, выполнять вычисления.

Итерации производятся до тех пор, пока ôERRô£ TOL. Если встречается седловая точка и не известно, куда направлен градиент, то выдается сообщение not converging (не решаемо). Количество итераций ограничено. Возможно сообщение об ошибке вида did not find solution (не найдено решение).

При возникновении таких ошибок можно:

– изменить точность – TOL;

– заменить начальные условия;

Видео:2 - Решениt систем линейных алгебраических уравнений (СЛАУ) с помощью Matlab.Скачать

– заменить find на minerr и получить приближенное решение.

Однако при использовании функций findи minerrнужно проявлять осторожность и обязательно предусматривать проверку решений, т.к. нередки случаи, когда решение может оказаться ошибочным.

Для получения другого решения можно поменять начальные условия, для уточнения – уменьшить TOL.

Пакет MATLAB

Рассмотрим две системы линейных уравнений: АХ=В и ХА=В. В MATLAB такие системы решаются без вычисления обратной матрицы. Два типа матричного деления / и используются для этих двух ситуаций, когда неизвестная матрица стоит слева или справа от матрицы коэффициентов:

Х=АВ соответствует решению АХ=В;

Х=В/А соответствует решению ХА = В.

При этом должны выполняться условия соответствия размерностей матриц X, А, В. Напомним, что для варианта Х=АВ матрица X должна иметь то же количество столбцов, что и матрица В, и то же число строк, сколько столбцов у матрицы А. Для Х=В/А эти условия обратны.

Алгебраические свойства оператора / можно вывести из соотношения(В/А)’ = (А’В’).

Матрица не обязательно должна быть квадратной, она может быть размером mхn. При этом существуют следующие варианты:

· m = n – квадратная система, возможно нахождение точного решения;

· m > n – переопределенная система, решение ищется с помощью метода наименьших квадратов;

· m n и ранг матрицы равен n, то каждое из трех следующих выражений вычисляет X по методу наименьших квадратов:

Видео:Решение произвольных уравнений. Методы вычислений в MATLAB. Часть 1. Урок 61Скачать

Х=АВ

Х=рinv(А)*В

Х=inv(А’*А)*А’*В

В противном случае решение Xпо методу наименьших квадратов не единственно и существует множество векторов, минимизирующих norm(A*X-B).Решение, вычисленное с помощью Х=АВ,– базовое решение, имеющее не больше r ненулевых компонент: r=rank(A). Решение, вычисленное с помощью Х=рinv(А)*В,– это решение с минимальной нормой X.