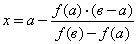Решение уравнения методом хорд эксель

Видео:Численное решение уравнений, урок 3/5. Метод хордСкачать

Решение нелинейных уравнений методом хорд в MS Excel

Тема урока: «Решение нелинейных уравнений в MS Excel».

Цель урока: изучение возможностей MS Excel по решению нелинейных уравнений и практическое освоение соответствующих умений и навыков.

Тип урока: комбинированный – урок изучения нового материала и практического закрепления полученных знаний, умений и навыков.

Вид урока: сдвоенный, продолжительность – 1,5 часа.

Задачи урока:

• обучающая – научить учащихся решать нелинейные уравнения в среде электронных таблиц MS Excel;
• развивающая – познакомить учащихся с применением компьютеров в качестве помощников при решении уравнений;
• воспитательная – выработать у учащихся умение рационально использовать время и возможности компьютерных технологий при решении задач.

Оборудование урока:

• Компьютеры с OS MS Windows;
• Программа Microsoft Excel;
• Программа Turbo Pascal;
• Презентация по теме, выполненная в программе Power Point;
• Карточки с заданиями для самостоятельной работы.

В данном уроке особое внимание уделено визуальному представлению информации – в ходе урока с помощью проектора демонстрируются слайды, подготовленные в пакете презентационной графики Microsoft Power Point.

I. Организационный момент

Учитель объявляет тему и цели урока.

II. Актуализация знаний, умений и навыков учащихся – повторение материала прошлого урока по теме «Решение нелинейных уравнений методом половинного деления»

Учащиеся повторяют указанный метод с помощью слайдов, подготовленных в пакете презентационной графики Microsoft Power Point метод половинного деления

Вопросы:

• Всегда ли существуют формулы для «точного» решения уравнений?
• Сформулируйте основное условие существования корня на заданном отрезке.
• Запишите уравнение, позволяющее определить координаты середины отрезка.
• Почему алгоритм решения этой задачи можно назвать циклическим?
• Какое действие в алгоритме повторяется?
• Определите условие, при котором действие алгоритма должно остановиться.

III. Изобразите блок-схему алгоритма. блок-схема

IV. Практическое задание с использованием программы на языке Turbo Pascal (Учащимся разрешено использовать программу, составленную на предыдущем уроке. Было решено уравнение y = x 3 – cos(x)) метод половинного деления TP

Задания для учащихся первой группы

Найти решение уравнения y = x 3 – cos(x) на отрезке [–1;1], при = 0,0001

Задания для учащихся второй группы

Найти решение уравнения y = x 3 – cos(x) на отрезке [–1;1], определить на каком шаге циклического алгоритма будет получено решение.

V. Изучение нового материала «Решение нелинейных уравнений методом хорд»

VI. Объяснить алгоритм решения уравнения f(x)=0 на отрезке [а;в] методом хорд с помощью слайдов, подготовленных в пакете презентационной графики Microsoft Power Point. метод хорд

Вопросы:

• Запишите уравнение, позволяющее определить координаты точки пересечения с осью ОХ.
• Почему алгоритм решения этой задачи можно назвать циклическим?
• Какое действие в алгоритме повторяется?
• Определите условие, при котором действие алгоритма должно остановиться.
• Изобразите блок-схему алгоритма блок-схема2

Этапы решения задачи

• Содержательная постановка задачи. Решение уравнения y = x 3 – cos(x) на отрезке [–1,4; 1,4] с точностью = 0,001.
• Визуализация решения задачи с помощью построения графика заданной функции с помощью процессора MS Excel, используя метод подбора параметра определить корень уравнения.
• Формальная математическая модель.
  • Задание математической формулы для отыскания корня уравнения на отрезке
  • Задание системы ограничений при использовании циклического алгоритма
  • Требование к диапазону задания переменных

Для формализации модели используем математические формулы.

уравнение прямой, проходящей через две точки, где x₁ = a, x₂ = в, y₁ = f(a), y₂ = f(в).

После математических преобразований уравнение примет вид .

Определим корень уравнения

• Блок схема алгоритма решения задачи блок-схема2
• Программа на языке Turbo Pascal метод хорд ТР
• Заполнение расчетной таблицы в программе MS Excel метод хорд xls

Видео:Решение нелинейных уравнений методом хордСкачать

Решение уравнений в EXCEL методом половинного деления, методом хорд и касательных.

При прохождении темы численные методы учащиеся уже умеют работать с электронными таблицами и составлять программы на языке паскаль. Работа комбинированного характера.Расчитана на 40 минут. Цель работы повторить и закрепить навыки паботы с программами EXCEL, ABCPascal. Материал содержит 2 файла. Один содержит теоретический материал, так как он и предлагается ученику . Во 2-м файле пример работы ученика Иванова Ивана.

Видео:Численный метод Ньютона в ExcelСкачать

Скачать:

Видео:1,2 Решение нелинейных уравнений методом хордСкачать

Предварительный просмотр:

Аналитическое решение некоторых уравнений, содержащих, например тригонометрические функции может быть получено лишь для единичных частных случаев. Так, например, нет способа решить аналитически даже такое простое уравнение, как cos x=x

Численные методы позволяют найти приближенное значение корня с любой заданной точностью.

Приближённое нахождение обычно состоит из двух этапов:

1) отделение корней, т.е. установление возможно точных промежутков [a,b], в которых содержится только один корень уравнения;

2) уточнение приближённых корней, т.е. доведение их до заданной степени точности.

Мы будем рассматривать решения уравнений вида f(x)=0. Функция f(x) определена и непрерывна на отрезке [а.Ь]. Значение х 0 называется корнем уравнения если f(х 0 )=0

Для отделения корней будем исходить из следующих положений:

• Если f(a)* f(b] a, b существует, по крайней мере, один корень
• Если функция y = f(x) непрерывна на отрезке [a, b], и f(a)*f(b) и f ‘(x) на интервале (a, b) сохраняет знак, то внутри отрезка [а, b] существует единственный корень уравнения

Приближённое отделение корней можно провести и графически. Для этого уравнение (1) заменяют равносильным ему уравнением р(х) = ф(х), где функции р(х) и ф(х] более простые, чем функция f(x). Тогда, построив графики функций у = р(х) и у = ф(х), искомые корни получим, как абсциссы точек пересечения этих графиков

Для уточнения корня разделим отрезок [а, b] пополам и вычислим значение функции f(х) в точке x sr =(a+b)/2. Выбираем ту из половин [a, x sr ] или [x sr ,b], на концах которых функция f(x) имеет противоположные знаки.. Продолжаем процесс деления отрезка пополам и проводим то же рассмотрение до тех пор, пока. длина [a,b] станет меньше заданной точности . В последнем случае за приближённое значение корня можно принять любую точку отрезка [a,b] (как правило, берут его середину). Алгоритм высокоэффективен, так как на каждом витке (итерации) интервал поиска сокращается вдвое; следовательно, 10 итераций сократят его в тысячу раз. Сложности могут возникнуть с отделением корня у сложных функций.

Для приближенного определения отрезка на котором находится корень можно воспользоваться табличным процессором, построив график функции

ПРИМЕР : Определим графически корень уравнения . Пусть f1(х) = х , a и построим графики этих функций. (График). Корень находится на интервале от 1 до 2. Здесь же уточним значение корня с точностью 0,001(на доске шапка таблицы)

Алгоритм для программной реализации

1. а:=левая граница b:= правая граница
2. m:= (a+b)/2 середина
3. определяем f(a) и f(m)
4. если f(a)*f(m)
5. если (a-b)/2>e повторяем , начиная с пункта2

Точки графика функции на концах интервала соединяются хордой. Точка пересечения хорды и оси Ох (х*) и используется в качестве пробной. Далее рассуждаем так же, как и в предыдущем методе: если f(x a ) и f(х*) одного знака на интервале , нижняя граница переносится в точку х*; в противном случае – переносим верхнюю границу. Далее проводим новую хорду и т.д.

Осталось только уточнить, как найти х*. По сути, задача сводится к следующей: через 2 точки с неизвестными координатами (х 1 , у 1 ) и (х 2 , у 2 ) проведена прямая; найти точку пересечения этой прямой и оси Ох.

Запишем уравнение прямой по двум точках:

В точке пересечения этой прямой и оси Ох у=0, а х=х*, то есть

, откуда

процесс вычисления приближённых значений продолжается до тех пор, пока для двух последовательных приближений корня х„ и х п _1 не будет выполняться условие abs(xn-x n-1 ) е — заданная точность

Сходимость метода гораздо выше предыдущего

Алгоритм различается только в пункте вычисления серединной точки- пересечения хорды с осью абсцисс и условия останова (разность между двумя соседними точками пересечения)

Уравнения для самостоятельного решения: (отрезок в excel ищем самостоятельно)

Видео:Метод Ньютона для решения нелинйеных уравнений в MS ExcelСкачать

Решение уравнений методом хорд в excel

При прохождении темы численные методы учащиеся уже умеют работать с электронными таблицами и составлять программы на языке паскаль. Работа комбинированного характера.Расчитана на 40 минут. Цель работы повторить и закрепить навыки паботы с программами EXCEL, ABCPascal. Материал содержит 2 файла. Один содержит теоретический материал, так как он и предлагается ученику . Во 2-м файле пример работы ученика Иванова Ивана.

Видео:Численное решение уравнений, урок 4/5. Метод касательных (Ньютона)Скачать

Скачать:

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Предварительный просмотр:

Аналитическое решение некоторых уравнений, содержащих, например тригонометрические функции может быть получено лишь для единичных частных случаев. Так, например, нет способа решить аналитически даже такое простое уравнение, как cos x=x

Численные методы позволяют найти приближенное значение корня с любой заданной точностью.

Приближённое нахождение обычно состоит из двух этапов:

1) отделение корней, т.е. установление возможно точных промежутков [a,b], в которых содержится только один корень уравнения;

2) уточнение приближённых корней, т.е. доведение их до заданной степени точности.

Мы будем рассматривать решения уравнений вида f(x)=0. Функция f(x) определена и непрерывна на отрезке [а.Ь]. Значение х 0 называется корнем уравнения если f(х 0 )=0

Для отделения корней будем исходить из следующих положений:

• Если f(a)* f(b] a, b существует, по крайней мере, один корень
• Если функция y = f(x) непрерывна на отрезке [a, b], и f(a)*f(b) и f ‘(x) на интервале (a, b) сохраняет знак, то внутри отрезка [а, b] существует единственный корень уравнения

Приближённое отделение корней можно провести и графически. Для этого уравнение (1) заменяют равносильным ему уравнением р(х) = ф(х), где функции р(х) и ф(х] более простые, чем функция f(x). Тогда, построив графики функций у = р(х) и у = ф(х), искомые корни получим, как абсциссы точек пересечения этих графиков

Для уточнения корня разделим отрезок [а, b] пополам и вычислим значение функции f(х) в точке x sr =(a+b)/2. Выбираем ту из половин [a, x sr ] или [x sr ,b], на концах которых функция f(x) имеет противоположные знаки.. Продолжаем процесс деления отрезка пополам и проводим то же рассмотрение до тех пор, пока. длина [a,b] станет меньше заданной точности . В последнем случае за приближённое значение корня можно принять любую точку отрезка [a,b] (как правило, берут его середину). Алгоритм высокоэффективен, так как на каждом витке (итерации) интервал поиска сокращается вдвое; следовательно, 10 итераций сократят его в тысячу раз. Сложности могут возникнуть с отделением корня у сложных функций.

Для приближенного определения отрезка на котором находится корень можно воспользоваться табличным процессором, построив график функции

ПРИМЕР : Определим графически корень уравнения . Пусть f1(х) = х , a и построим графики этих функций. (График). Корень находится на интервале от 1 до 2. Здесь же уточним значение корня с точностью 0,001(на доске шапка таблицы)

Алгоритм для программной реализации

1. а:=левая граница b:= правая граница
2. m:= (a+b)/2 середина
3. определяем f(a) и f(m)
4. если f(a)*f(m)
5. если (a-b)/2>e повторяем , начиная с пункта2

Точки графика функции на концах интервала соединяются хордой. Точка пересечения хорды и оси Ох (х*) и используется в качестве пробной. Далее рассуждаем так же, как и в предыдущем методе: если f(x a ) и f(х*) одного знака на интервале , нижняя граница переносится в точку х*; в противном случае – переносим верхнюю границу. Далее проводим новую хорду и т.д.

Осталось только уточнить, как найти х*. По сути, задача сводится к следующей: через 2 точки с неизвестными координатами (х 1 , у 1 ) и (х 2 , у 2 ) проведена прямая; найти точку пересечения этой прямой и оси Ох.

Запишем уравнение прямой по двум точках:

В точке пересечения этой прямой и оси Ох у=0, а х=х*, то есть

, откуда

процесс вычисления приближённых значений продолжается до тех пор, пока для двух последовательных приближений корня х„ и х п _1 не будет выполняться условие abs(xn-x n-1 ) е – заданная точность

Сходимость метода гораздо выше предыдущего

Алгоритм различается только в пункте вычисления серединной точки- пересечения хорды с осью абсцисс и условия останова (разность между двумя соседними точками пересечения)

Уравнения для самостоятельного решения: (отрезок в excel ищем самостоятельно)

Метод хорд [7] заключается в замене кривой y = f(x) отрезком прямой, проходящей через точки (a, f(a)) и (b, f(b)) (см. рис. 2.6). Абсцисса точки пересечения прямой с осью OX принимается за очередное приближение.

Чтобы получить расчетную формулу метода хорд, запишем уравнение прямой, проходящей через точки (a, f(a)) и (b, f(b)) и, приравнивая y нулю, найдем x:

.

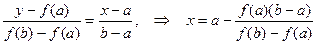
Рис.2.6. Метод хорд

Алгоритм метода хорд:

3) Если f(x_k)= 0 (корень найден), то переходим к 5).

5) Выводим значение корня x_k.

Замечание.Действия третьего пункта аналогичны действиям метода половинного деления. Однако в методе хорд на каждом шаге может сдвигаться один и тот же конец отрезка (правый или левый), если график функции в окрестности корня выпуклый вверх (рис. 2.6, a)) или вогнутый вниз (рис. 2.6, b)). Поэтому в критерии сходимости используется разность соседних приближений.

Пример 2.6. Применим метод хорд к уравнению sin 5x + x 2 – 1 = 0 и отрезку [0,2; 0,3] для определения корня с точностью до ε = 0,001.

Решение. Проведем расчеты в программе Excel:

1) В ячейки A1:H1 запишем заголовки столбцов как в табл. 2.6;

2) В ячейку B3 запишем формулу =ЕСЛИ(C2*E2

Решение в программе Mathcad:

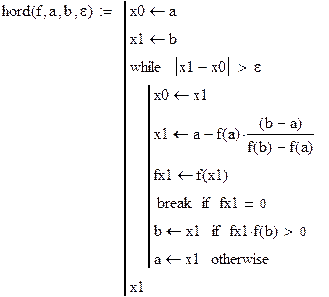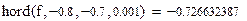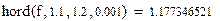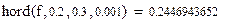Как видим, результаты расчетов согласуются с предыдущими ответами.

Приведем программу, которая реализует метод хорд на языке C++:

double f(double x);

typedef double (*PF)(double);

double hord(PF f,double a, double b,double eps, int Kmax);

double a, b, x, eps;PF pf; int Kmax;

x = hord(pf,a,b,eps, Kmax); cout > a;

double f(double x) 0) b = xk1;

>while (xerr > eps);

Результат расчета для примера 2.6:

Press any key & Enter

Как видим, результат совпадает с предыдущими расчетами.

Дата добавления: 2015-04-25 ; Просмотров: 3757 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Тема урока: «Решение нелинейных уравнений в MS Excel».

Цель урока: изучение возможностей MS Excel по решению нелинейных уравнений и практическое освоение соответствующих умений и навыков.

Тип урока: комбинированный – урок изучения нового материала и практического закрепления полученных знаний, умений и навыков.

Вид урока: сдвоенный, продолжительность – 1,5 часа.

Задачи урока:

• обучающая – научить учащихся решать нелинейные уравнения в среде электронных таблиц MS Excel;
• развивающая – познакомить учащихся с применением компьютеров в качестве помощников при решении уравнений;
• воспитательная – выработать у учащихся умение рационально использовать время и возможности компьютерных технологий при решении задач.

Оборудование урока:

• Компьютеры с OS MS Windows;
• Программа Microsoft Excel;
• Программа Turbo Pascal;
• Презентация по теме, выполненная в программе Power Point;
• Карточки с заданиями для самостоятельной работы.

В данном уроке особое внимание уделено визуальному представлению информации – в ходе урока с помощью проектора демонстрируются слайды, подготовленные в пакете презентационной графики Microsoft Power Point.

I. Организационный момент

Учитель объявляет тему и цели урока.

II. Актуализация знаний, умений и навыков учащихся – повторение материала прошлого урока по теме «Решение нелинейных уравнений методом половинного деления»

Учащиеся повторяют указанный метод с помощью слайдов, подготовленных в пакете презентационной графики Microsoft Power Point метод половинного деления

Вопросы:

• Всегда ли существуют формулы для «точного» решения уравнений?
• Сформулируйте основное условие существования корня на заданном отрезке.
• Запишите уравнение, позволяющее определить координаты середины отрезка.
• Почему алгоритм решения этой задачи можно назвать циклическим?
• Какое действие в алгоритме повторяется?
• Определите условие, при котором действие алгоритма должно остановиться.

III. Изобразите блок-схему алгоритма. блок-схема

IV. Практическое задание с использованием программы на языке Turbo Pascal (Учащимся разрешено использовать программу, составленную на предыдущем уроке. Было решено уравнение y = x 3 – cos(x)) метод половинного деления TP

Задания для учащихся первой группы

Найти решение уравнения y = x 3 – cos(x) на отрезке [–1;1], при 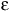= 0,0001

Задания для учащихся второй группы

Найти решение уравнения y = x 3 – cos(x) на отрезке [–1;1], определить на каком шаге циклического алгоритма будет получено решение.

V. Изучение нового материала «Решение нелинейных уравнений методом хорд»

VI. Объяснить алгоритм решения уравнения f(x)=0 на отрезке [а;в] методом хорд с помощью слайдов, подготовленных в пакете презентационной графики Microsoft Power Point. метод хорд

Вопросы:

• Запишите уравнение, позволяющее определить координаты точки пересечения с осью ОХ.
• Почему алгоритм решения этой задачи можно назвать циклическим?
• Какое действие в алгоритме повторяется?
• Определите условие, при котором действие алгоритма должно остановиться.
• Изобразите блок-схему алгоритма блок-схема2

Этапы решения задачи

• Содержательная постановка задачи. Решение уравнения y = x 3 – cos(x) на отрезке [–1,4; 1,4] с точностью = 0,001.
• Визуализация решения задачи с помощью построения графика заданной функции с помощью процессора MS Excel, используя метод подбора параметра определить корень уравнения.
• Формальная математическая модель.

• Задание математической формулы для отыскания корня уравнения на отрезке
• Задание системы ограничений при использовании циклического алгоритма
• Требование к диапазону задания переменных

Для формализации модели используем математические формулы.

уравнение прямой, проходящей через две точки, где x₁ = a, x₂ = в, y₁ = f(a), y₂ = f(в).

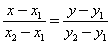
После математических преобразований уравнение примет вид .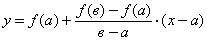

Определим корень уравнения

• Блок схема алгоритма решения задачи блок-схема2
• Программа на языке Turbo Pascal метод хорд ТР
• Заполнение расчетной таблицы в программе MS Excel метод хорд xls

🎦 Видео

Численное решение уравнений, урок 5/5. Комбинированный метод хорд и касательныхСкачать

Решение нелинейного уравнения методом хордСкачать

Алгоритмы. Нахождение корней уравнения методом хордСкачать

Метод секущихСкачать

Метод хордСкачать

Решение нелинейного уравнения методом хорд (секущих) (программа)Скачать

5.1 Численные методы решения уравнений F(x)=0Скачать

Решение уравнений с помощью ExcelСкачать

метод хордСкачать

Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Метод хорд для приближённого решения алгебраических уравненийСкачать

Метод Хорд - ВизуализацияСкачать

12 Метод Ньютона (Метод касательных) Excel Calc Численные методы решения нелинейного уравненияСкачать