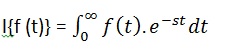Дата добавления: 2015-06-12 ; просмотров: 11107 ; Нарушение авторских прав
Преобразование Лапласа любой комплексной функции f(t) действительной переменной t имеет вид
Функцию f(t) принятоназывть оригиналом, а функцию L(s) – изображением. Функция f(t) должна удовлетворять следующим условиям:
а) f(t) является непрерывной функцией для всех значений t, принадлежащих области определения. (Допускается наличие разрывов первого рода в конечном числе точек, расположенных на интервалах конечной длины. Количество таких интервалов должно быть конечным числом);
б) f(t) = 0 при t 0 и p ≥ 0 такие, что для всех t │f(t)│ pt (p называется показателем роста │f(t)│).
Некоторые простейшие) преобразования Лапласа приведены в таблице 7.1.
Таблица 7.1.Некоторые преобразования Лапласа
| f(t) | L(s) = f(t)e -st dt. |
| 1 | s -1 |
| e -at | (s+a) -1 |
| sinat | a(s 2 +a 2 ) -1 |
| t n | n!s -n-1 |
| e -at coswt | |
| t n e -at |
В MATLAB преобразование Лапласа функции f(t) осуществляется с помощью команды laplace(F,t,s).
Найдем с помощью этой команды изображения заданных в таблице 7.1 оригиналов f(t):
- MATLAB — Преобразования
- Преобразование Лапласа
- пример
- Обратное преобразование Лапласа
- laplace
- Syntax
- Description
- Examples
- Laplace Transform of Symbolic Expression
- Specify Independent Variable and Transformation Variable
- Laplace Transforms of Dirac and Heaviside Functions
- Relation Between Laplace Transform of Function and Its Derivative
- Laplace Transform of Array Inputs
- Laplace Transform of Symbolic Function
- If Laplace Transform Cannot Be Found
- Input Arguments
- f — Input symbolic expression | symbolic function | symbolic vector | symbolic matrix
- var — Independent variable t (default) | symbolic variable
- transVar — Transformation variable s (default) | z | symbolic variable | symbolic expression | symbolic vector | symbolic matrix
- More About
- Laplace Transform
- Algorithms
- 📺 Видео
Видео:7.1 Решение уравнения Лапласа в прямоугольникеСкачать

MATLAB — Преобразования
MATLAB предоставляет команду для работы с преобразованиями, такими как преобразования Лапласа и Фурье. Преобразования используются в науке и технике как инструмент для упрощения анализа и анализа данных с другой стороны.
Например, преобразование Фурье позволяет нам преобразовывать сигнал, представленный как функцию времени, в функцию частоты. Преобразование Лапласа позволяет преобразовать дифференциальное уравнение в алгебраическое уравнение.
MATLAB предоставляет команды laplace , fourier и fft для работы с преобразованиями Laplace, Fourier и Fast Fourier.
Видео:2 - Решениt систем линейных алгебраических уравнений (СЛАУ) с помощью Matlab.Скачать

Преобразование Лапласа
Преобразование Лапласа функции времени f (t) задается следующим интегралом:
Преобразование Лапласа также обозначается как преобразование f (t) в F (s). Вы можете видеть, что этот процесс преобразования или интеграции преобразует функцию f (t) символической переменной t в другую функцию F (s) с другой переменной s.
Преобразование Лапласа превращает дифференциальные уравнения в алгебраические. Чтобы вычислить преобразование Лапласа функции f (t), напишите —
пример
В этом примере мы вычислим преобразование Лапласа некоторых часто используемых функций.
Создайте файл сценария и введите следующий код —
Когда вы запускаете файл, он показывает следующий результат —
Видео:MatLab. Решение дифференциального уравнения.Скачать

Обратное преобразование Лапласа
MATLAB позволяет нам вычислять обратное преобразование Лапласа, используя команду ilaplace .
Видео:Лекция 124. Преобразование Лапласа. ВведениеСкачать

laplace
Видео:Метод Лапласа решения ДУСкачать

Syntax
Видео:Решение произвольных уравнений. Методы вычислений в MATLAB. Часть 1. Урок 61Скачать

Description
laplace( f ) returns the Laplace Transform of f . By default, the independent variable is t and the transformation variable is s .
laplace( f , transVar ) uses the transformation variable transVar instead of s .
laplace( f , var , transVar ) uses the independent variable var and the transformation variable transVar instead of t and s , respectively.
Видео:MatLab. 6.1. Решение уравненийСкачать

Examples
Laplace Transform of Symbolic Expression
Compute the Laplace transform of 1/sqrt(x) . By default, the transform is in terms of s .
Specify Independent Variable and Transformation Variable
Compute the Laplace transform of exp(-a*t) . By default, the independent variable is t , and the transformation variable is s .
Specify the transformation variable as y . If you specify only one variable, that variable is the transformation variable. The independent variable is still t .
Specify both the independent and transformation variables as a and y in the second and third arguments, respectively.
Laplace Transforms of Dirac and Heaviside Functions
Compute the Laplace transforms of the Dirac and Heaviside functions.
Relation Between Laplace Transform of Function and Its Derivative
Show that the Laplace transform of the derivative of a function is expressed in terms of the Laplace transform of the function itself.
Laplace Transform of Array Inputs
Find the Laplace transform of the matrix M . Specify the independent and transformation variables for each matrix entry by using matrices of the same size. When the arguments are nonscalars, laplace acts on them element-wise.
If laplace is called with both scalar and nonscalar arguments, then it expands the scalars to match the nonscalars by using scalar expansion. Nonscalar arguments must be the same size.
Laplace Transform of Symbolic Function
Compute the Laplace transform of symbolic functions. When the first argument contains symbolic functions, then the second argument must be a scalar.
If Laplace Transform Cannot Be Found
If laplace cannot transform the input then it returns an unevaluated call.
Return the original expression by using ilaplace .
Видео:Решение уравнения Лапласа в шареСкачать

Input Arguments
f — Input
symbolic expression | symbolic function | symbolic vector | symbolic matrix
Input, specified as a symbolic expression, function, vector, or matrix.
var — Independent variable
t (default) | symbolic variable
Independent variable, specified as a symbolic variable. This variable is often called the «time variable» or the «space variable.» If you do not specify the variable then, by default, laplace uses t . If f does not contain t , then laplace uses the function symvar to determine the independent variable.
transVar — Transformation variable
s (default) | z | symbolic variable | symbolic expression | symbolic vector | symbolic matrix
Transformation variable, specified as a symbolic variable, expression, vector, or matrix. This variable is often called the «complex frequency variable.» If you do not specify the variable then, by default, laplace uses s . If s is the independent variable of f , then laplace uses z .
Видео:Преобразование Лапласа - bezbotvyСкачать

More About
Laplace Transform
The Laplace transform F = F( s) of the expression f = f( t) with respect to the variable t at the point s is
F ( s ) = ∫ 0 – ∞ f ( t ) e − s t d t .
If any argument is an array, then laplace acts element-wise on all elements of the array.
If the first argument contains a symbolic function, then the second argument must be a scalar.
To compute the inverse Laplace transform, use ilaplace .
Видео:Уравнение Лапласа (ФКП)Скачать

Algorithms
The Laplace transform is defined as a unilateral or one-sided transform. This definition assumes that the signal f( t) is only defined for all real numbers t ≥ 0 , or f( t) = 0 for t . Therefore, for a generalized signal with f( t) ≠ 0 for t , the Laplace transform of f( t) gives the same result as if f( t) is multiplied by a Heaviside step function.
📺 Видео
Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

1 - Решение систем нелинейных уравнений в MatlabСкачать

ТАУ. Matlab/SIMULINK Фазовые портреты нелинейных и линейных диф. уравненийСкачать

Символьные и численные расчеты в MATLABСкачать

Решение систем Д/У: 2. Опции решателей odeXYСкачать

Преобразование Лапласа по определениюСкачать

MatLab. 7.9. Системы дифференциальных уравненийСкачать