Министерство образования и науки РФ
БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
“ВОЕНМЕХ” им. Д.Ф. Устинова
Кафедра ракетостроение
Отчет по лабораторной работе №2
Компьютерное обеспечение технических решений
Выполнил: Сафиулин Р.Т.
Проверил: Степанов М.М.
ЛАБОРАТОРНАЯ РАБОТА №2
Видео:Решение уравнения теплопроводности методом конечных разностейСкачать

Решение дифференциальных уравнений в частных производных эллиптического типа методом конечных разностей
(на примере двумерного уравнения Лапласа)
Цель работы
· изучение конечно-разностных методов решения дифференциальных уравнений в частных производных эллиптического типа на примере двумерного уравнения Лапласа;
· освоение наиболее распространенных простейших разностных схем решения этого уравнения;
· исследование свойств разностных схем;
· изучение методов решения получающихся систем линейных алгебраических уравнений;
· изучение возможных алгоритмов реализации данных методов на ЭВМ;
Краткие сведения из теории
3.2.1. Двумерным уравнением Лапласа называется следующее дифференциальное уравнение в частных производных второго порядка эллиптического типа:
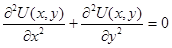
Видео:6-2. Метод сетокСкачать

Это уравнение часто встречается в приложениях и описывает целый ряд важных физических процессов:
§ напряжения, возникающие при упругом кручении цилиндрического стержня;
§ распределение потенциалов (или электрических напряжений) на проводящей плоскости при задании потенциала на ее границе;
§ стационарные (установившиеся) поля температур в двумерном твердом теле;
§ дозвуковое (потенциальное) течение газа и т.д.
Для корректной постановки задачи необходимо задание соответствующих граничных условий. Если граничные условия задаются в виде
U(x,y)│s = f(x,y) , где S — граница рассматриваемой области, (4)
то задача носит название «задачи Дирихле».
Используемые методы
«Прямые» методы решения уравнения Лапласа
Видео:Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

В данной лабораторной работе для решения указанного уравнения в качестве «прямого» метода предлагается использовать схему Рунге (другое название «пятиточечная схема»). Будучи примененная к уравнению Лапласа в сочетании с последующим использованием для решения получающейся системы линейных алгебраических уравнений итерационного метода Гаусса — Зайделя, она получила название «метода Либмана». Именно метод Либмана используется в данной лабораторной работе.
Схема Рунге (пятиточечная схема)
Простейшая пятиточечная схема выглядит следующим образом:


Модифицированное уравнение (дифференциальное приближение) этой схемы имеет следующий вид:
Схема имеет второй порядок аппроксимации. Абсолютно согласована. Превалируют диссипативные ошибки.
При ∆x=∆y разностные уравнения имеют вид:

Уравнение (5) или (как в данной лабораторной работе) уравнение (6) записывается для всех узлов сетки, в которых величина U(i,j) неизвестна, т.е. для всех ее «внутренних» узлов. Если задача решается в квадрате, каждая сторона которого разбита N точками на (N-1) отрезков, то (при граничных условиях Дирихле) в каждом из внутренних узлов должно удовлетворяться разностное уравнение (5) или (6). При этом необходимо одновременно решать (N-2)*(N-2) линейных алгебраических уравнений с (N-2)*(N-2) неизвестными.
В данной лабораторной работе используется итерационный метод Гаусса-Зайделя, который при применении к уравнению Лапласа часто, как уже отмечалось, называют методом Либмана (ω=1). Для ускорения сходимости данного итерационного процесса используется метод последовательной верхней релаксации с ускоряющим множителем ω, причем 

Как отмечалось, в данной лабораторной работе используется также метод последовательной верхней релаксации с ускоряющим множителем ω, причем 1

Уравнение Лапласа
Многие стационарные физические задачи, т.е. такие, в которых рассматриваются явления, неизменные с течением времени (исследования потенциальных течений жидкости, определение формы нагруженной мембраны, задачи теплопроводности и диффузии в стационарных случаях и др.) сводятся к решению уравнения Пуассона вида

Если 

Видео:РК6. Модели и методы анализа проектных решений. Метод конечных разностей, двумерные задачиСкачать

Решение этого уравнения будем искать для некоторой ограниченной области Gизменения независимых переменных х, у. Границей области Gявляется замкнутая линия L. Для полной формулировки краевой задачи кроме уравнения Лапласа нужно задать граничное условие на границе L. Примем его в виде

Задача, состоящая в решении уравнения Лапласа (или Пуассона) при заданных значениях искомой функции на границе расчетной области, называется задачей Дирихле.
Одним из способов решения стационарных эллиптических задач, в том числе и краевой задачи (2.89), (2.90), является их сведение к решению некоторой фиктивной нестационарной задачи (гиперболической или параболической), найденное решение которой при достаточно больших значениях времени tблизко к решению исходной задачи. Такой способ решения называется методом установления.
Поскольку решение U(x,y) уравнения (2.89) не зависит от времени, то можно в это уравнение добавить равный нулю (при точном решении) член ¶U/¶t. Тогда уравнение (2.89) примет вид

Это известное нам уравнение теплопроводности, для которого в разд. 2.3.2, 2.3.3 уже строили разностные схемы. Остается только задать начальное условие. Его можно принять практически в произвольном виде, согласованном с граничными условиями. Примем

Граничное условие (2.90) при этом остается стационарным, т. е. не зависящим от времени.
Процесс численного решения уравнения (2.91) с условиями (2.92), (2.90) состоит в переходе при t→∞ от произвольного значения (2.92) к искомому стационарному решению. Счет ведется до выхода решения на стационарный режим. Естественно, решением ограничиваются при некотором достаточно большом t, если искомые значения на двух последовательных слоях совпадают с заданной степенью точности.
Метод установления фактически представляет итерационный процесс решения задачи (2.91) с условиями (2.92), (2.90), причем на каждой итерации значения искомой функции получаются путем численного решения некоторой вспомогательной задачи. В теории разностных схем показано, что этот итерационный процесс сходится к решению исходной задачи, если такое стационарное решение существует.
Другой способ решения задачи Дирихле состоит в построении разностной схемы путем аппроксимации уравнения (2.89). Введем в прямоугольной области Gсетку с помощью координатных прямых х = const и у = const. Примем для простоты значения шагов по переменным х и у равными h(предполагается, что стороны области Gсоизмеримы). Значения функции Uв узлах (xi, yj) заменим значениями сеточной функции uij. Тогда, аппроксимируя в уравнении (2.89) вторые производные с помощью отношений конечных разностей, получим разностное уравнение (шаблон изображен на рис. 2.27).

Рис. 2.27. Шаблон для уравнения Лапласа
Видео:Метод конечных разностей - проверка результатов LiraSaprСкачать

С помощью данного уравнения можно записать систему линейных алгебраических уравнений относительно значений сеточной функции в узлах в виде

Значения сеточной функции в узлах, расположенных на границе расчетной области, могут быть найдены из граничного условия (2.90):
В теории разностных схем доказывается, что решение построенной разностной задачи существует, а сама схема устойчива.
Перейдем теперь, к практическому вычислению искомых значений, т.е. к решению системы (2.94). Каждое уравнение системы (за исключением тех, которые соответствуют узлам, расположенным вблизи границ) содержит пять неизвестных. Одним из наиболее распространенных методов решения этой системы линейных уравнений является итерационный метод. Каждое из уравнений записываем в виде, разрешенном относительно значения uij в центральном узле (см. рис. 2.27):

Алгоритм решения задачи Дирихле с использованием итерационного метода Гаусса-Зейделя решения системы разностных уравнений (2.95) изображен на рис. 2.28. В алгоритме предусмотрен выбор начальных значений uij. Иногда полагают, что uij=0 для всех i, j.
Рис. 2.28. Алгоритм решения задачи Дирихле
Итерационный процесс контролируется максимальным отклонением М значений сеточной функции в узлах для двух последовательных итераций. Если его значение достигнет некоторого заданного малого числа ε,итерации прекращаются и происходит вывод результатов.
Рассмотренные разностные схемы метода сеток используют конечно-разностные аппроксимации входящих в уравнения производных по всем переменным. В ряде случаев уравнение с частными производными удобно привести к системе обыкновенных дифференциальных уравнений, в которых оставлены производные искомой функции лишь по одной переменной.
Такой способ можно использовать и для решения уравнения Лапласа (2.89). Пусть требуется решить для него задачу Дирихле в прямоугольнике ABCD(рис. 2.29). Разобьем прямоугольник на полосы с помощью прямых, параллельных оси х. Для определенности проведем три отрезка l1, l2, l3, которые разделят прямоугольник на четыре полосы постоянной ширины h. Решение Uзадачи Дирихле приближенно заменим набором функций ui,каждая из которых определена на отрезке li и зависит только от одной переменной х, т.е.ui= ui(х) (i = 1,2,3). На отрезках l0 и l4 значения u0(x) и u4(x) заданы граничными условиями.
Рис. 2.29. К решению задачи Дирихле в прямоугольнике ABCD
Видео:Метод Лапласа решения ДУСкачать

Построим разностную схему для определения значений функций u(х). Аппроксимируя в уравнении (2.89) вторую производную по у с помощью отношения конечных разностей, получаем

Таким образом, решение задачи Дирихле (2.89), (2.90) сводятся к решению краевой задачи для системы обыкновенных дифференциальных уравнений (2.96) относительно значений искомой функции вдоль прямых l1, l2, l3. В этом состоит метод прямых. Граничные условия для уравнений (2.96) при х = а, х = bможно получить из уравнений
Направление дискретизации у обычно легко выбрать в тех случаях, когда заранее известен характер поведения искомой функции, это направление должно соответствовать направлению наибольшей гладкости функции.
Метод прямых широко используют для решения нестационарных задач. Например, если имеются две независимые переменные х, t, а искомый параметр является гладкой функцией переменной х, то дискретизацию вводят по этой переменной. Тогда исходную задачу заменяют задачей Коши для системы обыкновенных дифференциальных уравнений вида:
🎦 Видео
Решение уравнения теплопроводности в одномерной постановке в ExcelСкачать

7.1 Решение уравнения Лапласа в прямоугольникеСкачать

Численные методы. Лекция 14: метод конечных разностей решения краевой задачиСкачать

Тихонов Н. А. - Основы математического моделирования - Метод конечных разностей (Лекция 7)Скачать

Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Решение уравнения Лапласа в шареСкачать

Основы метода конечных элементов. Часть 3. Основные уравнения теории упругости в МКЭСкачать

Классические точные аналитические методы решения уравнений гиперболического и параболического типаСкачать

Задача Дирихле для круга. Уравнение ЛапласаСкачать

Уравнение ЛапласаСкачать

8.1 Решение уравнения теплопроводности на отрезкеСкачать

6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольцеСкачать
Метод конечных элементов. Основы 1.1.1 - ВведениеСкачать

РК6. Модели и методы анализа проектных решений. Метод конечных разностей: неравномерные сеткиСкачать







