Решение уравнения колебания струны закрепленной на концах методом разделения переменных примеры (3 видео)

Метод Фурье

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Метод Фурье, или метод разделения переменных, является одним из наиболее распространенных методов решения уравнений с частными производными. Рассмотрим этот метод, обратившись к простейшей задаче о свободных колебаниях однородной струны длины i, закрепленной на концах. §4. Свободные колебания однородной струны, закрепленной на концах Задача о свободных колебаниях однородной струны с закрепленными концами сводится к решению уравнения при граничных условиях и начальных условиях.

Метод Фурье Задачу (1 )-(3) называют смешанной: она содержит и начальные и граничные условия. Решение задачи начнем с поиска частных решений уравнения (1) вида При этом будем предполагать, что каждое из них удовлетворяет граничным условиям (2), но не равно нулю тождественно. Подставляя функцию и<х, t) в форме (4) в уравнение (1), получаем ИЛИ Последнее равенство (его левая часть зависит только от а правая — только от х) возможнолишь втом случае, если обе его части не зависят ни от ty ни от х,т.е. равны одной и той же постоянной.

Обозначим эту постоянную (разделения) через (-А), Из равенства (5) получаем два обыкновенных дифференциальных уравнения Граничные условия (2) дают откуда (T(t) £ 0) следует, что функция Х(х) должна удовлетворять граничным условиям Чтобы получить нетривиальные решения tt(x, t) вида (4), удовлетворяющие граничным условиям (2), необходимо найти нетривиальные решения уравнения удовлетворяющие граничным условиям.

Таким образом, мы приходим к следующей задаче: найти значения параметра А, при которых существуют нетривиальные решения задачи (7)-(8), а также сами эти решения. Такие значения параметра А называются собственными значениями, а соответствующие им нетривиальные решения — собственными функциями задачи (7)-(8). Сформулированную таким образом задачу называют задачей Штурма—Лиувилля. Найдем собственные значения и собственные функции задачи (7)-(8).

Рассмотрим отдельно три случая, когда 1.

При общее решение уравнения (7) имеет вид Потребовав выполнения граничных условий (8), получим (6) (7) Так как определитель системы (9) отличен от нуля, то . Следовательно, Х(х) = 0, т. е. при нетривиальных решений задачи не существует. (9) 2. При А = 0 общее решение уравнения (7) имеет вид Граничные условия (8) дают откуда С, = С2 = 0, и следовательно, при А = 0 нетривиальных решений задачи (7)-(8) также не существует. 3.

При Л > 0 общее решение уравнения (7) имеет вид Потребовав выполнение граничных условий (8), получим Система (10) имеет нетривиальные решениятогда и толькотогда, когда определитель системы равен нулю, Метод Фурье будут собственными функциями задачи. Собственные функции определены с точностью до постоянного множителя, который мы выбрали равным единице. При А = А* общее решение у равнения (6) имеетвид ктга кчга где Аки Bk — произвольные постоянные. Таким образом, функции удовлетворяют уравнению (1) и граничным условиям (2) при любых Ак и Вку В силу линейности и однородности уравнения (1) всякая коневая сумма решений будет также решением уравнения (1).

То же справедливо и для ряда если он сходится равномерно и его можно дважды почленно дифференцировать по х и по t. Поскольку каждое слагаемое в ряде (11) удовлетворяет граничным условиям (2), то этим условиям будет удовлетворять и сумма u(s, t) этого ряда. Остается определить в формуле (11) постоянные .4* и Вк так, чтобы выполнялись и начальные условия (3). Продифференцируем формально ряд (11) по t.

Имеем Полагая в соотношениях (l 1) и (12) t = 0, в силу начальных условий (3) получим Формулы (13) представляют собой разложения заданных функций вряд Фурье по синусам в интервале Коэффициенты разложений (13) вычисляются по известным формулам / I Теорема 2. Если и удоъчетворяет условиям и удовлетворяет условию то сумма tx(x, £) ряда (11), где -А* и В* опредыяются формулами (14), имеет в области непрерывные частные производные до второго порядка включительно по каждому из аргументов, удовлетворяет уравнению (1), граничным условиям (2) и начальным условиям (3), т. е. является решением задачи (1 )-(3).

Пример. Найти закон свободных колебаний однородной струны длины I, закрепленной на концах, если в начальный момент t = 0 струна имеет форму параболы — const), а начальная скорость отсутствует. 4 Задача сводится к решению уравнения при граничных условиях и начальных условиях.

Возможно вам будут полезны данные страницы:

Содержание

Метод Фурье
Первое из граничных условий
Электронная библиотека
Метод Фурье (метод разделения переменных) для уравнения свободных колебаний струны
🌟 Видео

Метод Фурье

Применяя метод Фурье, ищем нетривиальные решения уравнения (1), удовлетворяющие граничным условиям (2), в виде Подставляя «(*,*) в форме (4) в уравнение (1) и разделяя переменные, получим откуда причем в силу (2) Как было установлю но выше, собственные значения задачи (7)-(8) а соответствующие собственные функции Для А = Ащ общее решение уравнения (6) имеет вид пяа ижа Будем иска тъ решение исходной задачи в виде ряда Для определен ия коэффициентов -4Я и Z?„ воспользуемся начальными условия ми (3).

Имеем Из формулы (II) срезу

получаем, что 2?„ = 0 для любог о п, а из (10) Метод Фурье откуда, интегрируя по частям дважды . находи м . Подставляя наеденные значения А, и в ряд (9), получим решение поставленной задачи , Замечание. Если начальные фукхдда не удовлетворяют условиям теоремы 2, то дважды непрерывно дифференцируемого решения смешанной задачи (1)-(3) может и не существовать.

Однако если , то ряд (II) сходетс* равномерно при и любом t и определяет непрерывную функюао u(xtt). В этом случае можно говорить лишь об обобщенная решении задачи. Каждая из функций определяет так называемые собств енные колебания струны, закрепленной на концах. При собственных колебаниях, отвечающих к = 1, струна издает основной, самый низкий тон.

При колебаниях, соответствующих ббльшим Л.она издает более высокие тоны, обертоны. Записав *) в виде заключаем, что собственные колебания струны — стоячие волны, при которых точки струны совершают гармонические колебания с амплитудой Нк sin частотой Метод Фурье Мы рассмотрели случай свободных колебаний однородной струны, закрепленной на концах. Рассмотрим теперьслуч ай других граничных условий.

Пусть, например, левый конец струны закреплен, u(0, t) = 0, а правый конец х — 1 упругосвязан со своим положением равновесия, что соответствует условию . Нетривиальное решение u(x, t) уравнения (1), удовлетворяющее поставленным граничным условиям, будем опять искать в виде В результате подстановки в уравнение (1) приходим к следующей задаче о собственных значениям: найти такие значения параметра Л, для которых дифференциальное уравнение при граничных условиях имеет нетривиальные решения Х(х). Общее решение уравнения (15) имеет вид (А > 0)

Первое из граничных условий

Первое из граничных условий (16) дает С = 0, так что функциями Х(х) с точностью до постоянного множителя являются sin у/Хх. Из второго граничного условия Положим А = ir. Тогда Для отыскания и получаем трансцендентное уравнение. Корни этого уравнения можно найти графически, взяв в плоскости (f, z) сечения последовательных ветвей кривой z = tg(i//) прямой линией z = (рис. 7).

Обе части уравнения (18) — нечетные функции относительно р, поэтому каждому положительному корню i/fc соответствует равный ему по абсолютной величине отрицательный корень. Поскольку изменение знака Uk не влечет за собой появления новых собственных функций (они только изменят знак, что несущественно), достаточно ограничиться положительными корнями уравнения (18).

В результате опять получается последовательность собственных значений и отвечающие им последовательности собственных функций и собственных колебаний Кстати, для n-ой собственной частоты ип получается асимптотическое соотношение в частности, для I = т имеем Если правый конец струны х = I свободен, получаем cos vl = 0. Отсюда ul = § + тиг, так что в случае свободного конца собственные значения и собственные функции соответственно равны

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Электронная библиотека

Метод разделения переменных, или метод Фурье, или метод наложения стоячих волн, является одним из важнейших методов решения уравнений математической физики. Найдем решение задачи о свободных колебаниях конечной струны, закрепленной на концах, методом Фурье, то есть будем искать решение уравнения:

удовлетворяющее однородным или нулевым граничным условиям

и начальным условиям

Рассмотрим основную вспомогательную задачу.

Найти отличные от тождественного нуля решения уравнения (4.31), удовлетворяющие только граничным условиям (4.32), в виде произведения:

то есть в виде произведения функции только от x на функцию только от t. Такой подход дает возможность выбирать одну из функций или произвольно. Используя такой подход при решении уравнения (4.31), получим:

Поделив полученное выражение на , будем иметь:

Левая часть этого выражения зависит только от x, правая – только от переменного t. Так как последнее равенство справедливо для любых значений x и t (можно, например, зафиксировать x и менять t), то левая и правая части сохраняют постоянное значение, которое для удобства дальнейших выкладок обозначим так:

В результате получим два обыкновенных дифференциальных уравнения:

Учитывая граничные условия (4.32), получим:

Нетрудно проверить, что если постоянная отрицательна или равна нулю, то не существует отличной от тождественного нуля функции , удовлетворяющей краевым условиям (4.36). Поэтому постоянная должна быть положительна. Для функции в основной вспомогательной задаче дополнительных условий нет.

Задача решения уравнения (4.34) с условиями (4.36) называется задачей о собственных значениях или задачей Штурма-Лиувилля.

Ненулевое решение уравнения (4.34) запишется в виде:

Из граничных условий находим:

Так как , то , поэтому .

Числа называются собственными значениями краевой задачи (задачи Штурма-Лиувилля). Им соответствуют функции:

где – произвольные постоянные, которые называются собственными функциями.

Ввиду произвольности выбора одной из функций или положим .

Тем же собственным значениям будут соответствовать решения уравнения (4.35):

где , – произвольные постоянные.

Итак, частными решениями основной вспомогательной задачи будут функции:

Сумма частных решений также является решением этой задачи:

Если определить и по начальным условиям (4.33), то тем самым мы найдем решение поставленной задачи (4.31) – (4.33).

Подставив в выражение (4.37), получим:

аналогично для производной :

Чтобы найти и , используем теорию рядов Фурье, из которой известно, что произвольная кусочно-непрерывная и кусочно-дифференцируемая функция , то есть функция, удовлетворяющая условиям Дирихле, заданная в промежутке , разлагается в ряд Фурье по синусам:

Если функции и удовлетворяют условиям Дирихле, то

Сравнение этих рядов с формулами (4.38) и (4.39) показывает, что для выполнения начальных условий (4.33) надо положить:

Таким образом, окончательно, решение задачи о свободных колебаниях конечной струны с закрепленными концами имеет вид:

Очевидно, ряд (4.40) должен сходиться, а функция должна быть дифференцируемой. В противном случае выражение (4.40) не может быть решением рассматриваемого дифференциального уравнения.

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Видео:Уравнение колебания струны. Решение методом ДаламбераСкачать

Метод Фурье (метод разделения переменных) для уравнения свободных колебаний струны

Определим закон свободных колебаний однородной струны размером l (0 0), для которой в начальный момент времени (при t = 0) заданы смещение равное φ(x) и его скорость равная ψ(x). При этом концы струны жестко закреплены. Математически эту задачу можно записать следующим образом

, (16.1)

(16.2)

. (16.3)

Будем искать нетривиальные частные решения уравнения (16.1), удовлетворяющие условиям (16.2) и (16.3), в виде произведения двух функций, зависящих только от одного аргумента X=X(x) и T=T(t), а именно

, (16.4)

Вычислив производные от (16.4) и, подставив их в уравнение (16.1), получим

(16.5)

. (16.6)

Равенство (16.6) выполняется только в том случае, если обе части его не зависят ни от х, ни от t, т.е. представляют собой одну и туже постоянную, которую обозначим за , т.е.

. (16.7)

Отсюда получаем два обыкновенных однородных линейных уравнений второго порядка

(16.8)

. (16.9)

Для того, чтобы получить не равные нулю решения вида (16.4), удовлетворяющие граничным условиям (16.3), необходимо найти нетривиальные решения, удовлетворяющие граничным условиям

. (16.10)

Таким образом, мы пришли к задаче: найти такие значения параметра l, которые, назовем собственными числами или собственными значениями. Нетривиальные решения уравнения (16.9), которые соответствуют этим собственным значениям, назовем собственными функциями, удовлетворяющие граничным условиям (16.10). Задачу отыскания собственных значений и собственных функций называют задачей Штурма-Лиувилля.

Рассмотрим три случая задачи (16.9), (16.10)

1) l 0.

В этом случае общее решение уравнения (16.9) имеет вид

удовлетворяя граничным условиям (16.10), получим

В уравнении постоянная С₂ не может быть равной нулю, поскольку в этом случае, мы получим тривиальное решение задачи (16.9), (16.10) — Х(х) ≡ 0. Поэтому для того, чтобы равенство выполнялось необходимо, чтобы выполнялось равенство , а оно выполняется только тогда, когда (n-любое целое число). Следовательно, нетривиальное решение задачи (16.9), (16.10) возможно лишь при собственных значениях l_n равных

. (16.11)

Только этим собственным значениям соответствуют (нормированные) собственные функции вида

, (16.12)

которые будут являться нетривиальными решениями задачи (16.9), (16.10).

Собственные значения (16.12) подставим в уравнение (16.8)

. (16.13)

Общее решение этого уравнения имеет вид

. (16.14)

Подставляя функции (16.12) и (16.14) в (16.4), найдем

, (16.15)

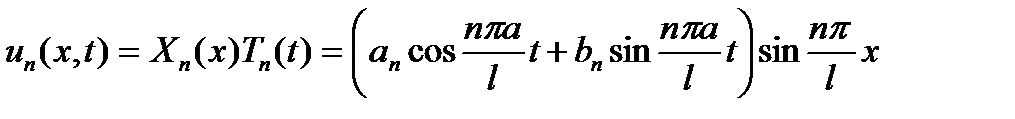
Эта функция удовлетворяет уравнению (16.1) и граничным условиям (16.3) при любых коэффициентах a_k и b_k. В силу линейности и однородности уравнения (16.1) всякая конечная сумма решений (16.15) также будет решением уравнения (16.1), поэтому можно записать

. (16.16)

Для определения значений постоянных a_n и b_n необходимо воспользоваться начальными условиям (16.2). Удовлетворяя в решении (16.16) первому из условий (16.2), получим

. (16.17)

Это равенство представляет собой разложение функции φ(x) в ряд Фурье по синусам. Следовательно, постоянная a_n является коэффициентом ряда Фурье в интервале (0,l), который можно определить по формуле

. (16.18)

Для определения коэффициента b_n, вычислим производную по t от функции (16.16)

и удовлетворим в решении (16.16) второму из условий (16.2), в результате получим

. (16.19)

Это равенство представляет собой разложение функции ψ(x) в ряд Фурье по синусам. Следовательно, постоянная b_n является коэффициентом ряда Фурье в интервале (0,l), который можно определить по формуле

. (16.20)

Таким образом, ряд (16.16) полностью определяет решение исходной краевой задачи (16.1)-( 16.3).

Пример 16.1. Определить закон свободных колебаний однородной струны единичного размера (0 0), для которой в начальный момент времени (при t = 0) начальное смещение равно нулю, а его скорость равна x=(1-х). При этом концы струны жестко закреплены. Математически эту задачу можно записать следующим образом

, (П16.1.1)

, (П16.1.2)

. (П16.1.3)

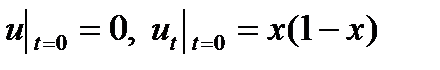
▲Будем этой задачи, будем искать в виде (16.4)

, (П16.1.4)

Вычислив производные от (П16.1.4) и, подставив их в уравнение (П16.1.1), проведя вышеописанные преобразования, получим два уравнения для нахождения функций X=X(x) и T=T(t)

(П16.1.5)

. (П16.1.6)

Для того, чтобы получить не равные нулю решения вида (П16.1.4), удовлетворяющие граничным условиям (П16.1.3), необходимо найти нетривиальные решения, удовлетворяющие граничным условиям

. (П16.1.7)

Общее решение уравнения (П16.1.6) имеет вид

удовлетворяя граничным условиям (П16.1.7), получим

Нетривиальное решение задачи (П16.1.6), (16.1.7) возможно лишь при собственных значениях λ_n равных

. (П16.1.8)

Только этим собственным значениям соответствуют (нормированные) собственные функции вида

, (П16.1.9)

которые будут являться нетривиальными решениями задачи (П16.1.6), (П16.1.7).

Собственные значения (П16.1.8) подставим в уравнение (П16.1.5)

Общее решение этого уравнения имеет вид

. (П16.1.10)

Подставляя функции (П16.1.9) и (П16.1.10) в (П16.1.4), найдем

. (П16.1.11)

Для определения значений постоянных a_n и b_n воспользуемся начальными условиям (П16.1.2). Удовлетворяя в решении (П16.1.11) первому из условий (П16.1.2), получим

Следовательно, постоянная a_n =0

Для определения коэффициента b_n удовлетворим в решении (П16.1.11) второму из условий (П16.1.2), в результате получим

Это равенство представляет собой разложение функции x(1-х) в ряд Фурье по синусам. Следовательно, постоянная b_n является коэффициентом ряда Фурье в интервале (0,l), который можно определить по формуле

.(16.20)

Вычислим оба интеграла

подставим найденные интегралы в (16.20)

Подставив найденное значение коэффициента b_n в решение (П16.1.11), получим окончательный вид решения исходной задачи

.▲

Пример 16.2. Струна, закрепленная на концах x=0 и x=l, имеет в начальный момент форму параболы . Определить смещение точек струны от оси абсцисс, если начальные скорости отсутствуют.