Решение уравнения f x 0 или нахождение нулей функции осуществляется с помощью функции (5 видео)

Содержание

Нули функции онлайн
Основные теоретические сведения. В системе MATLAB для решения систем линейных уравнений предусмотрены знаки операций / и
Что такое нули функции и как их определить
Примеры
Алгоритм определения
Типичные ошибки
Графическое представление
🔍 Видео

Видео:Как найти нули функции? #shortsСкачать

Нули функции онлайн

Одной из задач, возникающих при исследовании функции, является нахождение её нулей — т.е. точек пересения с осью абсцисс. Рассмотрим график некоторой функции :

Нулями функции являются точки в которых, как было сказано выше, график функции пересекает ось абсцисс. Чтобы найти нули функции необходимо и достаточно решить уравнение:

Нулями функции будут корни этого уравнения. Таким образом, нули функции находятся в точках .

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha способен найти нули практически любой, даже очень сложной функции.

Видео:7 класс, 36 урок, Что означает в математике запись y = f(х)Скачать

Основные теоретические сведения. В системе MATLAB для решения систем линейных уравнений предусмотрены знаки операций / и

В системе MATLAB для решения систем линейных уравнений предусмотрены знаки операций / и . Чтобы решить систему линейных уравнений вида

где A – заданная квадратная матрица размером NxN,

B – заданный вектор–столбец длины N, достаточно применить операцию и вычислить выражение A B .

Операция называется левым делением матриц и, будучи примененная к матрицам A и B в виде AB , примерно эквивалентна вычислению выражения inv(A)*B. Здесь под inv(A) понимается вычисление матрицы, обратной к матрице A . Операцию / называют правым делением матрицы. Выражение A/B примерно соответствует вычислению выражения B*inv(A). Значит, эта операция позволяет решать системы линейных уравнений вида y⋅A= B .

Решение уравнения F(x)=0, или нахождение нулей функции, осуществляется с помощью функции fzero(name, x₀) . В качестве первого аргумента ей передается имя функции, задающей исходное уравнение, вторым аргументом служит начальное приближение к корню. Определим, в качестве примера, нули функции cos(x) на отрезке от 0 до pi. В качестве начального приближения примем x₀=1.

Если требуется найти корень функции, отличной от стандартной (встроенной в систему MATLAB) и тем самым не имеющей в рамках системы MATLAB фиксированного имени, то нужно приписать некоторое имя выражению, вычисляющему функцию.

Пусть, например, требуется найти корни уравнения cos(x)=x, что эквивалентно нахождению нулей функции, вычисляемой по формуле y=cos(x)−x, не имеющей в рамках системы MATLAB фиксированного имени. В этом случае нужно создать Mat–функцию вида

function y=MyFunction1(x)

После этого можно воспользоваться функцией fzero:

Если найдено абсолютно точное значение корня, то значение функции в этой точке равно нулю. Таким образом, величина функции в приближенно найденном нуле косвенно характеризует погрешность результата. Чтобы управлять погрешностью, нужно осуществлять вызов функции fzero с тремя аргументами fzero(name, x₀, tol ), где tol задает требуемую величину погрешности (ошибки). Необходимо отметить, что функция fzero находит нули только вещественнозначных функций одной вещественной переменной. Однако часто бывает необходимо найти комплексные корни вещественнозначных функций, особенно в случае многочленов. Для этой цели в системе MATLAB существует специальная функция roots(p), которой в качестве аргумента передается массив коэффициентов многочлена (p). Например, для многочлена нужно сначала сформировать массив его коэффициентов (расположив по порядку убывания степени х):

В задаче о нахождении нулей функции сложным моментом является нахождение начального приближения к нулю функции, а также априорная оценка их количества. Поэтому важно параллельно с применением функций типа roots или fzero визуализировать поведение искомых функций на том или ином отрезке значений аргумента.

В системе MATLAB имеются специальные функции для поиска минимума заданных функций. При этом возможен поиск минимума как для функции одной вещественной переменной, так и для функций многих переменных. Для функций одной переменной их минимумы разыскивает функция

xmin =fmin(name, x₀, x₁). Здесь name представляет имя функции, у которой находятся минимумы, а x₀ и x₁ задают отрезок поиска. Для поиска минимума функции нескольких переменных применяется функция fmins: xmins = fmins( name, x₀). Здесь name является именем функции нескольких переменных, для которой ищется минимум, а x₀ – это вектор ее аргументов, с которого начинается поиск. Для иллюстративного примера создадим простую функцию двух переменных имеющую минимумом точку (0,0).

function у = MyFunc2(х)

После этого можно вызвать функцию fmins, которая приближенно находит вектор xmin координат точки минимума:

>> xmin = fmins( ‘MyFunc2’, [1,1] );

Для вычисления интегралов методом трапеций в системе MATLAB предусмотрена функция trapz: Integ = trapz(х, у). Точность вычисления интеграла зависит от величины шага интегрирования: чем меньше этот шаг, тем больше точность.

Вычислим простой интеграл методом трапеций с шагом интегрирования рi/10.

Обычно для достижения высокой точности требуется выполнять интегрирование с очень малыми шагами, а контроль достигнутой точности осуществлять путем сравнения последовательных результатов. При одном и том же шаге интегрирования методы более высоких порядков точности достигают более точных результатов. В системе MATLAB методы интегрирования более высоких порядков точности реализуются функциями: quad (метод Симпcона) и quad8 (метод Ньюто-на-Котеса 8-го порядка точности).

Двойные интегралы в системе MATLAB вычисляются с помощью специальной функции dblquad.

Вычислим интеграл вида .

Оформим подынтегральную mat–функцию и вызовем функцию dblquad:

function z = integ(x, у)

z = x.*sin(y) + y.*sin(x);

>>J = dblquad( ‘integ’, 0, 1, 1, 2 );

Возможности встроенного пакета символьных вычислений и операции Symbolic Math Toolbox достаточно обширны, рассмотрим лишь некоторые его возможности. Символьный объект создается при помощи функции syms. Команда создает три символьные переменные х, а и b

Конструирование символьных функций от переменных класса sym object производится с использованием обычных арифметических операций и обозначений для встроенных математических функций. Запись формулы для выражения в одну строку не всегда удобна, более естественный вид выражения выводит в командное окно функция pretty:

Рисунок 5.1– Демонстрация работы функции pretty

Упростим выражение , используя функцию simplify.

Рисунок 5.2– Демонстрация работы функции simplify

Символьную функцию можно создать без предварительного объявления переменных при помощи sym, входным аргументом которой является строка с выражением, заключенная в апострофы:

Рисунок 5.3 – Демонстрация создания символьной переменной без предварительного объявления

Упрощение тригонометрических, логарифмических, экспоненциальных

функций и полиномов осуществляется функцией expand, формат обращения к которой имеет следующий вид: rez=expand(S), где S – символьное выражение, которое нужно упростить, rez – результат упрощения.

rezl = sin (x) *cos (у) +cos (x) *sin (y)

С помощью функции factor можно раскладывать многочлены на простые множители, а целые числа – в произведение простых чисел

Функция subs осуществляет подстановку новых выражений для указанных символьных переменных:

Рисунок 5.4– Демонстрация работы функции subs

Symbolic Math Toolbox позволяет работать как с неопределенными интегралами, так и с определенными. Неопределенные интегралы от символьных функций вычисляются при помощи функции int, в качестве входных аргументов указываются символьная функция и переменная, по которой происходит интегрирование (см. рис.5.5).

Рисунок 5.5– Демонстрация работы функции int

Для нахождения определенного интеграла в символьном виде следует задать нижний и верхний пределы интегрирования, соответственно, в третьем и четвертом аргументах int:

Рисунок 5.6– Демонстрация работы функции intдля нахождения определенного интеграла

Перечислим еще несколько функций, часто используемых при символьных вычислениях:

inv – вычисляет обратную матрицу;

limit –вычисляет пределы;

taylor – осуществляет разложение функций в ряд Тейлора;

solve – решает алгебраическое уравнение и систему алгебраических уравнений.

Для работы с символьными данными предусмотрена оболочка funtool. Она представляет собой интерактивный графический калькулятор, позволяющий быстро построить графики двух функций и . Интерфейс данного приложения представлен на рисунке 5.7. При запуске выводятся три автономных окна: два графически и управляющее. Управляющее окно содержит два поля для ввода функций, поле ввода пределом изменения переменной x, поле ввода масштабирующего коэффициента.

Рисунок 5.7 – Интерфейс приложения funtool

Порядок выполнения

1. Составить и отладить программы для нахождения корней уравнения f1(x) = 0 и f2(x) = 0 и вывести графики функции на основании задания из таблицы 5.1.

2. Найти определенный интеграл для подынтегральной функции, заданной в таблице 5.2.

Таблица 5.1– Варианты заданий для нахождения корней уравнения

№ варианта	– полином 3-ей степени с коэффициентами a
-1	-1
-2	-15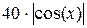
-1
-8	-70
-4
-5
-3
-6
-9
-7
-1	-4
-2	-6	-7
-3	-9	-8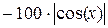
-4	-75
-5	-1

Таблица 5.2 – Варианты функций для нахождения значения интеграла

№ варианта	Функция	Интервал интегрирования
начало интервала	конец интервала
	-2
	-2
	-2
	-2
	-0.5	4.5
	-1.4	1.4
	-5
	-5
	-4
	-2
	-2
Продолжение таблицы 5.2
	-2
	-1
	-2
	-2

3. Найти определенный интеграл для подынтегральной функции, заданной в таблице 5.2 с использованием пакета символьных вычислений.

Содержание отчета

2. Листинг программы и результаты выполнения.

Контрольные вопросы

1.Для чего служит функция fmin?

2. Для чего служит функция fzero?

4. Перечислите основные внешние расширения системы MATLAB для поиска экстремумов функций.

5. Какая функция служит для вычисления определенного интеграла?

6. Назовите функции работы с символьными переменными.

Видео:Найти нули функции. 9 класс. АлгебраСкачать

Что такое нули функции и как их определить

Что такое нули функции? Ответит довольно прост — это математический термин, под которым подразумевают область определения заданной функции, на котором ее значение нулевое. Нули функции также называют корнями уравнения. Проще всего пояснить, что такое нули функции, на нескольких простых примерах.

Видео:Нули функции / Где они? / как их найти / Все про функции (урок 6)Скачать

Примеры

Рассмотрим несложное уравнение у=х+3. Поскольку нуль функции — это значение аргумента, при котором у приобрел нулевое значение, подставим 0 в левую часть уравнения:

В данном случае -3 и есть искомый нуль. Для данной функции существует только один корень уравнения, но так бывает далеко не всегда.

Рассмотрим другой пример:

Подставим 0 в левую часть уравнения, как и в предыдущем примере:

Очевидно, что в данном случае нулей функции будет два: х=3 и х=-3. Если бы в уравнении был аргумент третьей степени, нулей было бы три. Можно сделать простой вывод, что количество корней многочлена соответствует максимальной степени агрумента в уравнении. Однако многие функции, например у=х 3 , на первый взгляд противоречат этому утверждению. Логика и здравый смысл подсказывают, что у этой функции только один нуль — в точке х=0. Но на самом деле корней три, просто все они совпадают. Если решать уравнение в комплексной форме, это становится очевидным. х=0 в данном случае, корень, кратность которого 3. В предыдущем примере нули не совпадали, потому имели кратность 1.

Видео:СПОРИМ ты поймешь Математику — Функция и ее свойства, Область определения, Нули ФункцииСкачать

Алгоритм определения

Из представленных примеров видно, как определить нули функции. Алгоритм всегда один и тот же:

Записать функцию.
Подставить у или f(x)=0.
Решить получившееся уравнение.

Сложность последнего пункта зависит от степени аргумента уравнения. При решении уравнений высоких степеней особенно важно помнить, что количество корней уравнения равно максимальной степени аргумента. Особенно это актуально для тригонометрических уравнений, где деление обоих частей на синус или косинус приводит к потере корней.

Уравнения произвольной степени проще всего решать методом Горнера, который был разработан специально для нахождения нулей произвольного многочлена.

Значение нулей функций может быть как отрицательным, так и положительным, действительным или лежащим в комплексной плоскости, единичным или множественным. Или же корней уравнения может и не быть. Например, функция у=8 не приобретет нулевого значения ни при каком х, потому что она не зависит от этой переменной.

Уравнение у=х 2 -16 имеет два корня, и оба лежат в комплексной плоскости: х₁=4і, х₂=-4і.

Видео:Решение тригонометрического уравнения. Нахождение нулей функции. ПримерСкачать

Типичные ошибки

Частая ошибка, которую допускают школьники, еще не разобравшиеся толком в том, что такое нули функции, — это замена на ноль аргумента (х), а не значения (у) функции. Они уверенно подставляют в уравнение х=0 и, исходя из этого, находят у. Но это неправильный подход.

Другая ошибка, как уже упоминалось, сокращение на синус или косинус в тригонометрическом уравнении, из-за чего и теряется один или несколько нулей функции. Это не означает, что в таких уравнениях нельзя ничего сокращать, просто при дальнейших подсчетах необходимо учитывать эти «потерянные» сомножители.

Видео:Функция. Область определения функции. Практическая часть. 10 класс.Скачать

Графическое представление

Понять, что такое нули функции, можно с помощью математических программ, таких как Maple. В ней можно построить график, указав желаемое количество точек и нужный масштаб. Те точки, в которых график пересечет ось ОХ, и есть искомые нули. Это один из самых быстрых способов нахождения корней многочлена, особенно если его порядок выше третьего. Так что если есть необходимость регулярно выполнять математические расчеты, находить корни многочленов произвольных степеней, строить графики, Maple или аналогичная программа будет просто незаменима для осуществления и проверки расчетов.