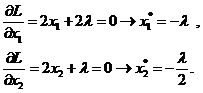Решение уравнения эйлера лагранжа онлайн

Назначение сервиса . Онлайн-калькулятор используется для нахождения экстремума функции через множители Лагранжа в онлайн режиме (см. пример и пример решения графическим способом). При этом решаются следующие задачи:

1. составляется функция Лагранжа L(X) в виде линейной комбинации функции F(X) и ограничений g_i(x);
2. находятся частные производные функции Лагранжа, ∂L/∂x_i, ∂L/∂λ_i;
3. составляется система из (n + m) уравнений, ∂L/∂x_i = 0.
4. определяются переменные x_i и множители Лагранжа λ_i.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Метод множителей Лагранжа применяется как в линейном программировании, так и в нелинейном. В экономике этот метод используется в задаче потребительского выбора.

Видео:Основы вариационного исчисления | уравнение Эйлера Лагранжа | 1Скачать

Правило множителей Лагранжа

Пример 1 . Методом множителей Лагранжа решить следующую задачу оптимизации:
min f(x) = x₁ 2 + x₂ 2
h₁(x) = 2x₁ + x₂ -2 = 0
Соответствующая задача оптимизации без ограничений записывается в следующем виде:
L(x, λ) = x₁ 2 + x₂ 2 + λ(2x₁ + x₂ – 2) → min
Решение:

Для того чтобы проверить, соответствует ли стационарная точка X минимуму, вычислим матрицу Гессе функции L(x, λ), рассматриваемой как функция от x,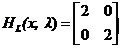
,
которая оказывается положительно определенной (2*2 – 0*0 = 4 > 0).
Это означает, что L(x, λ) – выпуклая функция. Следовательно, координаты x * = (-λ, λ/2) определяют точку глобального минимума. Оптимальное значение λ находится путем подстановки значений x₁ * и x₂ * в уравнение ограничений 2x₁ + x₂ -2 = 0, откуда вычисляем значение λ:
2λ + λ/2 = -2, откуда λ = -0.8
Таким образом, минимум достигается в точке x * с координатами x₁ * = 0.8 и x₂ * = 0.4. Значение ЦФ:
min f(x) = 0.8
Ответ: x * = [0.8; 0.4] T , f(x * ) = 0.8

Пример 2 . Исследовать на условный экстремум функцию f(x,y)_max = x 2 + 8xy+3y 2 при данных уравнениях связи.
9x +10y = 29

Видео:Основы вариационного исчисления | уравнение Эйлера Лагранжа | конкретные примеры | 1Скачать

Интерполяционный многочлен Лагранжа (полином Лагранжа)

Этот онлайн калькулятор строит интерполяционный многочлен Лагранжа для заданного набора точек. Калькулятор также строит график, на который выводит как полином Лагранжа, так и базисные полиномы, интерполирует заданные точки и показывает пошаговое решение.

Этот калькулятор может пригодиться при решении задач на интерполяцию полиномом Лагранжа. В таких задачах обычно требуется интерполировать значение неизвестной функции, соответствующее некоторому значению x, использую формулу интерполяционного многочлена Лагранжа, полученную из известного набора точек со значениями неизвестной функции (x, f(x)).

Калькулятор ниже обладает следующими функциями:

1. Он находит формулу полинома Лагранжа для заданного набора точек.
2. Он отображает пошаговый вывод формулы.
3. Он вычисляет значения интерполяционного многочлена Лагранжа для заданных точек (интерполирует функцию полиномом Лагранжа в заданных точках интерполяции)
4. Он отображает набор точек, значения в точках интерполяции, полином Лагранжа и все базисные полиномы на графике.

Как пользоваться

Сначала вводите набор точек — одна точка на строку в форме x f(x), значения разделены пробелом. Если вы хотите получить интерполяцию, вводите значения точек интерполяции в следующее поле в виде значений x, разделенных пробелом.

По умолчанию, калькулятор отображает формулу многочлена и его значения в точках интерполяции. Если нужно пошаговое решение, включите опцию «Показать пошаговое решение». Также можно отключить отображение базисных полиномов.

Теория и формулы, как обычно, описаны под калькулятором.

Видео:9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

🎬 Видео

Принцип наименьшего действия #2 - Уравнение Эйлера-ЛагранжаСкачать

Уравнение ЛагранжаСкачать

Курс по ОДУ: Уравнения Клеро и Лагранжа | Занятие 8Скачать

Основы вариационного исчисления | уравнение Эйлера Лагранжа | конкретные примеры | 3Скачать

№9. Элементы вариационного исчисления. Уравнения Лагранжа-Эйлера.Скачать

Семинар 3. Ужегов. Уравнение Эйлера.Скачать

Функция ЭйлераСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Уравнение Эйлера - bezbotvyСкачать

Основы вариационного исчисления | уравнение Эйлера Лагранжа | предварительные замечанияСкачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Основы вариационного исчисления | уравнение Эйлера Лагранжа | конкретные примеры | 2Скачать

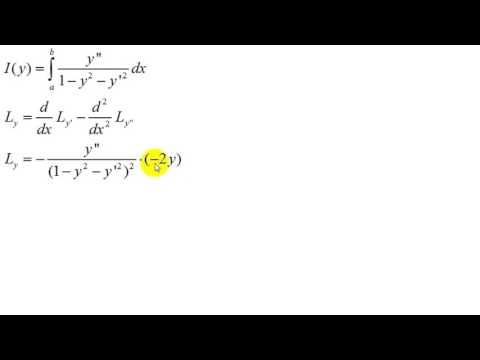
Решение системы дифференциальных уравнений методом ЭйлераСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Основы вариационного исчисления | уравнение Эйлера Лагранжа | конкретные примеры | 4Скачать