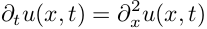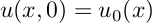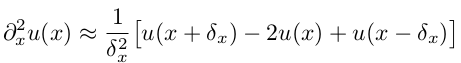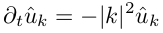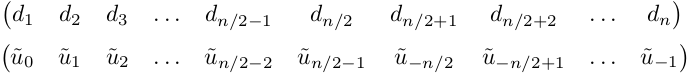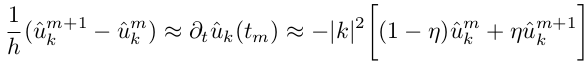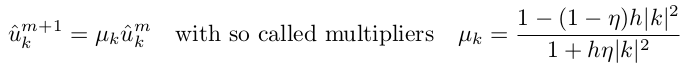Решение уравнения диффузии в плоской геометрии с источником граничные условия (6 видео)

Краевые задачи теории диффузии

Дифференциальное уравнение диффузии, выведенное на основе общих законов физики, устанавливает связь между временным и пространственным изменением концентрации в любой точке тела, в которой происходит диффузионный процесс. Дифференциальное уравнение диффузии имеет бесконечное множество решений. Чтобы из этого множества выбрать решение, характеризующее конкретный рассматриваемый процесс, и дать полное математическое описание процесса, необходимо к основному дифференциальному уравнению присоединить дополнительные условия, включающие геометрические, физические и краевые условия.

Геометрические условия определяют форму и линейные размеры тела.

Физические условия определяют физические параметры: коэффициент диффузии,

константу растворимости, объемную плотность потока диффузанта.

Краевыми условиями называют совокупность начального и граничного условий. Начальные условия задаются только при изучении нестационарных процессов и состоят в задании распределения концентрации внутри тела в момент времени, выбранный за начальный. Граничные условия отображают условия диффузионного взаимодействия между окружающей средой и поверхностью тела.

Граничные условия для изучаемой задачи могут быть заданы несколькими способами; в теории диффузии различают граничные условия I, II, III, IV родов. (Граничные условия IV рода иначе называют условиями сопряжения). Следует помнить, что число граничных условий превышает число границ. Так, в задаче по дегазации шарика (одномерный случай), необходимо задать условия как на внешней поверхности шарика, так и в центре. Часто граничные условия задаются «на бесконечности».

Граничные условия 1-го рода

В граничных условиях I – рода задается распределения концентрации диффузанта по поверхности Σ тела, как функция координат и времени.

В частном случае концентрация на поверхности – функция только времени

При наличии двух плоскостей (как это имеет место в методе газопроницаемости) задаются

две функции изменения концентрации диффузанта на входе в образец (например, пластину толщиной Н). Тогда граничные условия первого рода принимают вид:

Подобный режим в теории диффузии обозначается как граничная задача I-I.

В более простом случае – концентрация постоянна (условие Дирихле).

Если концентрация на границе в процессе эксперимента поддерживается равной нулю, то

вводится понятие поглощающей стенки.

Типичным примером, в котором на различных границах поддерживаются различные

варианты граничных условий первого рода, является случай проницаемости плоской мембраны толщиной Н. Здесь С(0,t)=C0, C(H,t)=0.

Условия 2-го рода

В условиях II – рода задается распределение плотности потока диффузанта для каждой точки поверхности как функция координат и времени

j = −D ∂C

где n — внутренняя нормаль к поверхности Σ.

Если поток за поверхности зависит от координаты, но не зависит от времени, граничное условие называется условием Неймана.

Важным частным случаем является отражающая стенка (отсутствие потока через внешние

поверхности образца – условие диффузионной изоляции):

В последнем случае граничная поверхность изолирована (диффузия через нее невозможна,

поток диффузанта через такую границу равен нулю).

Если образец имеет две границы (например, тонкая пластина), то в зависимости от условий на его внешних поверхностях различают граничные задачи II-II, I-II и II-I.

В центре шарика (сферы) поток отсутствует, следовательно, в центре – граничное условие

II-го рода (на поверхности I-го рода).

4.3 Условия 3-го рода

В граничных условиях III – рода задают закон конвективного массообмена между поверхностью тела и окружающей средой.

∂n Σ

– концентрация на поверхности; Cc

– концентрация примеси в окружающей среде, ks –

коэффициент пропорциональности, характеризующий интенсивность концентрационного взаимодействия среды с заданной концентрацией диффузанта Сс с поверхностью тела. В нестационарных процессах концентрация диффузанта в окружающей среде в общем случае изменяется во времени.

В этом случае на поверхности тела задается плотность потока диффузанта, возникающего из-за разности концентраций диффузанта на поверхности тела и в окружающей среде.

Ур.36 является аналитическим выражением граничного условия III рода, которое широко применяется при аналитических исследованиях массо-переноса в твердых телах, обтекаемых потоками жидкости или газа на границе между телом и флюидом.

Уравнение для упругой стенки полностью идентично уравнению Ньютона для теплообмена лучеиспусканием. Оно подразумевает, что концентрация не мгновенно устанавливается на поверхности, а в процессе некоторого времени, т.е. граница оказывает сопротивление диффузионному потоку (иногда более сильное, чем собственно диффузия). В этом случае поток не является постоянным, а изменяется как разность между концентрациями в твердом теле и в окружающем объеме.

Приведем вывод выражения для упругой стенки.

При справедливости закона Генри можно записать следующие выражения для потоков на поверхности твердого тела:

j1 = −k1C1x=0 →

поток газа из твердого тела;

поток из газа в твердое тело,

где k1 – константа дегазации; k2 – константа насыщения.

Если бы установилось равновесие, то

В нашем случае равновесия нет и

Внешний поток: k 2 p − k1C x=0 =

внут ∂x

x=0

jвнеш – т.к. нет накопления примеси на поверхности раздела фаз.

− D ∂C

D ∂C

x=0

Мы получили выражение, идентичное общему случаю.

= −

∂ ⎛ ⎞

Граничные условия III-го рода представляют собой общий случай. Из него может быть

получены выражения для условий I-го и II-го рода.

– условие I-го рода (закон

⎛ ⎞

Генри). При k = 0 , граничное условие II-го рода.

При сорбции C x=0 Cравн .

Граничные условия 3-го рода можно разделить на три категории: 1) Линейные; 2)

Нелинейные; 3) Нестационарные. Следует отметить, что наличие на поверхности (поверхностях) образца сложных химических процессов, в том числе — сопровождающихся выделением или поглощением тепла, приводит к граничным условиям 3-го рода весьма сложного вида.

В общем виде, при исследовании процессов диффузии в двустороннем образце возможно возникновение различных граничных задач: I-I, II-II, III-III, I-II, II-I, I-III, III-I, II-III, III-II, что может существенно затруднить обработку и интерпретацию данных диффузионных экспериментов.

К счастью, на практике часто встречаются согласованные (однородные нулевые)

CΣ = 0 – поглощающая стенка;

∂C

= 0 – отражающая стенка;

∂C + hC

= 0 – упругая стенка.

В первой части Курса лекций мы будем оперировать именно ими.

Условия 4-го рода

Граничные условия сопряжения (IV–рода) соответствуют массообмену поверхности тела с окружающей средой или массообмену соприкасающихся твердых тел, когда концентрация на соприкасающихся поверхностях одинакова (в случае газообразного диффузанта подчиняется закону Генри). Задаются они в виде

− D ∂C1

∂n

где Кр1 и Кр2 – константы растворимости, а D1 и D2 – коэффициенты диффузии диффузанта в

соприкасающихся средах 1 и 2, соответственно.

к поверхности раздела.

∂ означает дифференцирование вдоль нормали

Первое равенство выражает условие непрерывности концентрационного поля, а второе – закон сохранения энергии на поверхности соприкосновения двух сред (или тел) — Потоки на границе должны быть равны друг другу.

В отличие от случая теплопроводности где разрыва температуры на границе раздела фаз нет, в диффузии на границе раздела твердых тел возможны разрывы концентраций. Лишь в частном случае, при равенстве констант растворимости диффузанта в обеих фазах (при

Kp1 = K p2 ), то в точке

C1 = C2 и разрыва в концентрационном поле на границе фаз нет.

Содержание

МЕТОДЫ РЕШЕНИЯ ДИФФУЗИОННЫХ УРАВНЕНИЙ
Преобразование Фурье
Спектральный метод на примере простых задач матфизики
Одномерная задача распространения тепла по стержню
Двумерное уравнение диффузии
Двумерное волновое уравнение
Выводы
🌟 Видео

Видео:Решение уравнения теплопроводности в одномерной постановке в ExcelСкачать

МЕТОДЫ РЕШЕНИЯ ДИФФУЗИОННЫХ УРАВНЕНИЙ

Способов решения дифференциального уравнения в частных производных параболического типа довольно много. Продемонстрируемосо- бенности некоторых из них на конкретных примерах. Для сравнительного анализа эффективности различных математических подходов решим одну и ту же задачу тремя методами: методом Фурье, Лапласа и Грина.

Видео:Одномерное уравнение теплопроводности. Виды краевых задачСкачать

Преобразование Фурье

В начале 19века Ж.Фурье предложил метод решения дифференциальных уравнений, основанный на представлении периодических и гладких непериодических функций при помощи тригонометрических рядов. Ряд Фурье— представление произвольной функции/с периодом Т в виде ряда

где Ак — амплитуда к-го гармонического колебания, 2.71— = к (О — круговая

частота гармонического колебания, вк— начальная фаза к-го колебания, fk—k-я комплексная амплитуда.

Тригонометрический ряд Фурье функции / € Z,₂([ — функциональ

Числа а, а» и Ьп (п=1,2. п) называются коэффициентами Фурье функции/. Теорема Фурье (комплексный интеграл Фурье)—функция f(x) представима в виде интеграла:

Преобразование Фурье (?) — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разньши частотами. Преобразование Фурье функции / вещественной переменной является интегралом и задаётся формулой:

Если f(x) интегрируема, то к ней можно применить обратное преобразование Фурье, которое даёт исходную функцию.

Формула обращения Ферми:

На преобразовании Фурье базируется важный метод решения уравнений диффузии —метод разделения переменных.

Метод разделения переменных (Метод Фурье)— метод отыскания частных решений дифференциальных уравнений: путём специальных замен исходное уравнениеп переменных сводится к решению отдельных уравнений по меньшему числу переменных, в том числе к решению празличных уравнений для каждой перемен >юй.Методом Фурье решают линейные однородные уравнения.

Разделение переменных эффективно при решении дифференциальных уравнений параболического типа с постоянным коэффициентом диффузии при произвольном начальном распределении концентрации диффузанта по объёму образца.

Если рассматривается функция двутс переменных u(x,t), то метод Фурье включает следующие стадии:

— подстановка в исходное уравнение u(x,t)=X(x) T(t);
—получение двух уравнений относительно функций Х(х) и ДО;
— решение задачи Штурма-Лиувилля для функции Х(д:), нахождение собственных значений >.„и собственных функций^;
—нахождение для каждого X» функции T_n(t).

Решение уравнения имеет вид:

где коэффициенты С,определяются из начальных условий.

Задача Штурма-Лиувилля— задача о собственных значениях и собственных функциях. Для краевой задачи

Х(х)»+Л*(Х(х))=о; Х(о)=Х(1)=о; а Условие I-I. Концентрации на граничных поверхностях тождественно равны нулю:

Условие П-П. Так как диффузионный поток на двух граничных поверхностях равен нулю, градиент на этих поверхностях также равен нулю, производная от С на этих поверхностях равна нулю независимо от величины f, т.е. что ряд С содержит только косинусы (поскольку иначе градиент в точке л:=о не будет равен нулю) и все коэффициенты А в Ур.7 равны нулю. С другой стороны, значения sinctf^ Н равны нулю, что приводит к:

Условие II-I. Диффузионный поток на первой граничной поверхности равен нулю. Функция С содержит только косинусы. На второй граничной поверхности концентрация равна нулю, следовательно:

То же условие будет справедливо и для случая I—II.

Таким же образом можно получить значения (р в Ур.6.

Для определения амплитуд (коэффициентов а_т) воспользуемся начальным условием. Для расчёта коэффициентов а или эквивалентных коэффициентов А_т и В_т используется метод Фурье. Начальное распределение концентрации в пластине задаётся в виде C(₀)=fix).

Изменение концентрационного профиля во времени:

Если в момент времени t = О С($ = f (х) , то

Табл. 1 . Результаты согласованных условий I—II рода_

Индексы тип указывают на запись ряда, что позволяет опустить знак суммы.

Теперь найдём величину определенного интеграла:

вычисляемого от начала до конца линии диффузионного тока с такой точностью, с какой желательно получить коэффициент а_ш. Здесь:

Умножим правую и левую части Ур.9 на соъ(со_пх + (р_п) и возьмём интеграл (применим теорему Фурье):

где изменяется только п от нуля до бесконечности.

Условия (8) делают систему функций COs(rtK + (р) системой ортогональных функций на отрезке (о,Я), т.е. при т:^ = 0 •

При т = п, напротив:

Эти выражения позволяют рассчитать а_т, если известен

Согласно (и) имеем:

Расчёт коэффициентов а требует предосторожности в случае стенки с граничными условиями Н-Н (отражающие поверхности), когда функция С содержит только косинусы ( Пример 1. Задача на дегазацию пластины с произвольным начальным распределением концентрации (десорбция). Концентрация на поверхностях пластины поддерживается равной нулю в течение всего эксперимента, т.е. имеем условие I-I.

При больших временах ряд быстро сходится и можно ограничиться одним первым членом.

Количество диффузанта оставшееся в образце ко времени t: разца одинаковы.

Поток диффузанта, выходящий из одной из плоскостей пластины:

Если концентрация диффузанта на ограничивающих поверхностях

Пример 2. Диффузия в сфере радиуса R с равномерным начальным распределением концентрации C(o,f)=Qo) и концентрацией на поверхности С(Д,0=С_о.

Распределение концентрации диффузанта:

где г — текущая координата, г₀ — радиус шарика, А_п = 2*(—1)” +| ,

Пример з. Диффузия из бесконечно тонкого слоя в ограниченное твёрдое тело. Рассмотрим пластинку, в центре которой (в плоскости х=Н/2) расположен бесконечно тонкий источник диффундирующего вещества.

Рис. 1. Диффузия из бесконечно тонкого слоя в теле конечных размеров со связывающими границами: tl Пример 4. Диффузия из постоянного источника в образец (сорбция). Рассмотрим поглощение газа пластинкой толщиной Я.

Рис. 2. Диффузия из постоянного источника в тело конечных размеров: начальное условие С(л:,о); граничные условия: C(0,t)=C(H,t)=Co.

Будем искать решение задачи в виде

Изменение распределение концентрации диффузанта по толщине пластины описывается формулой:

Решение для распределения концентрации имеет вид:

Количество вещества поглощенное пластиной ко времени t:

Пример 5 . Диффузия в тело неограниченного размера из бесконечно тонкого импульсного источника.

Напомним, что для ограниченного тела ряд Фурье: а для бесконечного тела:

Воспользуемся интегральной теоремой Фурье, т.е. тем фактом, что практически любую функцию можно разложить на систему ортогональных функций синусов и косинусов:

Общее решение для бесконечного твёрдого тела:

Рис. з. Диффузия из импульсного бесконечно тонкого источника в бесконечную среду; значения Dt: 1/16 (1), 0,5 (2) и 1 (3).

Если бесконечно тонкий источник расположен в точке начал работать в момент времени т и проработал бесконечно малое время (бесконечно тонкий импульсный источник), количество попавшего в среду диффузанта М₀, то импульсная функция имеет вид:

М(о) — количество диффузанта, находящееся в бесконечно тонком слое при времени t= о [г/см 2 ].

Функция ехр(-д: 2 /4Dt) — чётная, поэтому распределения концентрации, создаваемые бесконечно тонким слоем в обоих полупространствах, симметричны относительно начала координат или середины слоя. Со временем начальное распределение постепенно расплывается, оставаясь симметричным относительно точки л:=о. _с м о уменьшается обратно

пропорционально корню квадратному из времени.

В трёхмерном случае:

Пример 6. Диффузия из слоя конечной толщины в бесконечную среду. Пусть в начальный момент времени концентрация примеси распределена равномерно в слое толщиной h.

где 0 — функция ошибок. Её основные свойства: erf (-у) = -erf у; erf0 = 0; erf’ж = 1

Рис. 4. Диффузия из слоя конечной толщины в неограниченное тело; значения (Dt/h-у/ 2 : о (1), 0,25(2), 0,5(3), 1(4), 2(5).

Дополнительная функция ошибок:

Интеграл дополнительной функции ошибок

Высота максимума на кривой распределения концентрации уменьшается обратно пропорционально корню квадратному из времени. При диффузии из слоя конечной толщины наблюдается тот же эффект, но он становится заметным через значительно большее время. Плоскость, в которой концентрация в е раз меньше, чем в плоскости дг=о, А’, = 2ylDt , т.е. расстояние между этими плоскостями изменяется пропорционально корню квадратному из времени.

Пример 7. Диффузия в полуограниченное тело из бесконечнотонкого источника, расположенного при координате

Воспользуемся решением для бесконечного тела:

Разобьём бесконечное тело на два полубесконечных, так что:

Тогда, распределение концентрации диффузанта:

Это выражение представляет собой общее решение диффузионного уравнения для полуограниченного тела. Функция Ci(-?,o) — неизвестна, ее можно определить из граничных условий.

Пример 8. Диффузия в полуограниченном теле со связывающей границей: односторонняя десорбция из полуограниченного твёрдого тела. Начальное условие: С=С(я:,о).

Граничное условие: C(o,f)=o при

Общее решение имеет вид:

А) Частный случай начального равномерного распределения С(х,о)=С(₀).

Рис. 5. Диффузия из полуограниченного тела со связывающей границей. Распределение концентрации:

Полученное решение описывает распределение концентрации в процессе односторонней дегазации полуограниченного твёрдого тела.

Б) Частный случай диффузии из постоянного источника (сорбция):

Рис. 6. Диффузия из постоянного источника в полуограниченное тело.

Общее количество диффузанта, поступившее в образец ко времени t:

Видео:Уравнения математической физики. Уравнение теплопроводности (диффузии).Скачать

Спектральный метод на примере простых задач матфизики

В этой статье описан псевдоспектральный метод численного решения уравнений матфизики, используемый в вычислительной гидродинамике, геофизике, климатологии и во многих других областях.

Одномерная задача распространения тепла по стержню

Для начала рассмотрим простую одномерную задачу распространения тепла в стержне. Уравнение, описывающее распространение тепла при некотором начальном распределении температуры по стержню:

Такое уравнение решается аналитически методом разделения переменных, например здесь, но нас интересует как это можно сделать численно. Прежде всего нужно определиться, как считать вторую пространственную производную по х. Проще всего это делается каким-нибудь разностным методом, например:

Но мы поступим иначе. Распределение температуры есть функция координаты и времени, и в каждый момент времени эта функция может быть представлена в виде суммы ряда Фурье, который в численном виде обрезается на n-ом члене:

Где u^«с крышечкой» — это коэффициенты разложения ряда Фурье. Подставим выражение для ряда в уравнение переноса тепла:

Получаем уравнение для коэффициентов Фурье, в котором отсутствует производная по координате! Теперь это обыкновенное дифференциальное уравнение, а не в частных производных, которое можно решить простым разностным методом. Уже легче, теперь остается найти коэффициенты разложения и в этом нам очень поможет быстрое преобразование Фурье (дальше FFT).

Логика здесь следующая:

1) в начальный момент времени дана функция координаты, описывающая распределение температуры по стержню;
2) разбиваем стержень на сетку из n точек;
3) находим комплексные коэффициенты Фурье с помощью алгоритма FFT, обозначим операцию как F(u);
4) умножаем полученные коэффиценты на -|k| 2 , получаем Фурье-образ второй производной. Аналогично можно получить Фурье-образ производной более высоких порядков p, достаточно умножить на (ik) p ;
5) делаем обратное преобразование Фурье F -1 (u), с помощью алгоритма IFFT, получаем значения второй производной в точках на сетке;
6) делаем шаг по времени, уже обычной разностной, явной или неявной, схемой;
7) повторяем.

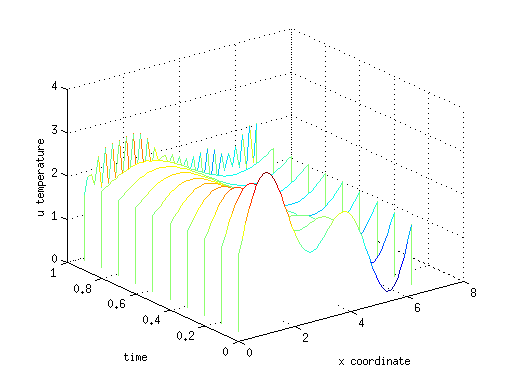
Рассмотрим теперь как это работает в программе для Matlab/Octave. В качестве начального распределения температуры возьмем гладкую функцию u0=2+sin(x)+sin(2x), стержень длинной 2π разобьем на 50 точек, с шагом по времени h=0.1, граничные условия периодичные (кольцо).

Стоит отметить особенность алгоритма FFT в Matlab, связанную с тем, что полученные коэффициенты разложения на выходе d=fft(u) идут не по порядку, а смещены, первая половина на месте второй и наоборот. Cначала идут коэффициенты с номерами от 0 до n/2-1, потом с номерами от -n/2 до -1. С этим были проблемы…

Полученное решение можно видеть на графике в виде «водопада» линий распределения температуры по х для каждого момента времени t. Видно, что решение испытывает ~~сильные осциляции~~ численную неустойчивость, связано это с невыполнением критерия Куранта. Избавиться от неустойчивости можно уменьшив шаг по времени, либо применяя более продвинутую неявную схему, например Кранка-Николсона.

Двумерное уравнение диффузии

Начальные условия: u0 = 1 + sin(2X) + cos(2Y), где u теперь 2d-массив u(i,j). Используем неявную схему интегрирования по времени (т.е. выразим m+1 шаг через m-й):

Можно доказать, что такая неявная схема никогда не расходится при η>0.5, будем использовать η=1. Таким образом каждое новое значение u m+1 получаем умножением u m на коэффициент μ_k, зависящий от временного шага и волновых чисел k, т.е. μ_k — это константа, которую не нужно пересчитывать на каждом шаге!

Двумерное волновое уравнение

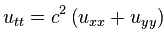
В волновом уравнении присутствует вторая производная по времени, поэтому задача сводится к системе двух обыкновенных диффуров, одна переменная — u, вторая — u_t, схему по времени в коде использовал самую простую явную, поэтому точность небольшая, шаг по времени очень маленький, зато код выглядит относительно просто. Впрочем, этого хватает для демонстрации работоспособности метода.

Периодичные граничные условия:

Фиксированные граничные условия (0 на краях, отражение волн от границ):

Выводы

В статье продемонстрировано несколько примеров применения спектрального метода для простых задач матфизики. Основная суть суть спектрального метода, это замена исходных диффренциальных уравнений в частных произодных на обыкновенные диффуры для коэффициентов разложения искомых функций по некоторому базису. Базисом могут быть синусы-косинусы, комплексные экспоненты, ортогональные полиномы, если требует геометрия — цилиндрические или сферические функции. Найденные коэффициенты в каждый момент времени позволяют восстановить искомое решение, а алгоритм FFT позволяет делать это быстро.

Преимуществами метода являются:

Хорошая точность для «хороших» функций. С увеличением количества точек сетки n ошибка метода конечных разностей падает как O(N -m )) (где m — некая постоянная, которая зависит от порядка метода и гладкости функции), а для спектрального метода точность может быть экспоненциальной O(c N ), где 0