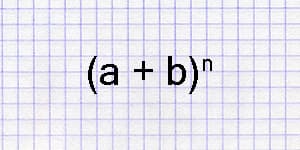Решение уравнения бинома ньютона онлайн

Видео:Бином Ньютона. Практическая часть. 10 класс.Скачать

Формула Бинома Ньютона

Для натурального n формула принимает такой вид:

(a + b) n = C 0 _n · a n + C 1 _n · a n-1 · b + C 2 _n · a n-2 · b 2 + … + C n-1 _n · a · b n-1 + C n _n · b n ,

где C k _n – биномиальные коэффициенты.

• (x + y) 2 = x 2 + 2 · x · y + y 2 ,
• (x + y) 3 = x 3 + 3 · x 2 · y + 3 · x · y 2 + y 3 ,
• (x + y) 4 = x 4 + 4 · x 3 · y + 6 · x 2 · y 2 + 4 · x · y 3 + y 4 ,
• (x + y) 5 = x 5 + 5 · x 4 · y + 10 · x 3 · y 2 + 10 · x 2 · y 3 + 5 · x · y 4 + y 5 ,

Видео:Бином Ньютона максимально простым языкомСкачать

Треугольник Паскаля

Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, которые для удобства восприятия записаны в форме треугольника. На его вершинах и по боковым сторонам стоят единицы, а каждое число равно сумме двух чисел над ним.

Видео:Бином Ньютона. 10 класс.Скачать

Метод Ньютона

Инструкция . Введите выражение F(x) , нажмите Далее . Полученное решение сохраняется в файле Word . Также создается шаблон решения в Excel .

• Решение онлайн
• Видеоинструкция
• Оформление Word

Правила ввода функции, заданной в явном виде

2. Примеры правильного написания F(x) :
   1. 10•x•e 2x = 10*x*exp(2*x)
   2. x•e -x +cos(3x) = x*exp(-x)+cos(3*x)
   3. x 3 -x 2 +3 = x^3-x^2+3
   4. Выражение 0.9*x=sin(x)+1 необходимо преобразовать к виду: sin(x)+1-0.9*x . Аналогично, x^2-7=5-3x к виду x^2+3x-12 .

   Пусть дано уравнение f(x)=0 , где f(x) определено и непрерывно в некотором конечном или бесконечном интервале a ≤ x ≤ b . Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ)=0 называется корнем уравнения или нулем функции f(x) . Число ξ называется корнем k -ой кратности, если при x = ξ вместе с функцией f(x) обращаются в нуль ее производные до (k-1) порядка включительно: f(ξ)=f’(ξ)= … =f k-1 (ξ) = 0 . Однократный корень называется простым.
   Приближенное нахождение корней уравнения складывается из двух этапов:

   1. Отделение корней, то есть установление интервалов [α_i,β_i] , в которых содержится один корень уравнения.
      1. f(a)•f(b) , т.е. значения функции на его концах имеют противоположные знаки.
      2. f’(x) сохраняет постоянный знак, т.е. функция монотонна (эти два условия достаточны, но НЕ необходимы) для единственности корня на искомом отрезке).
      3. f”(x) сохраняет постоянный знак, т.е. функция выпукла вверх, либо – вниз.
   2. Уточнение приближенных корней, то есть доведение их до заданной точности.

   Видео:Бином Ньютона и его свойства. 9 класс.Скачать

   

   Геометрическая интерпретация метода Ньютона (метод касательных)

   Критерий завершения итерационного процесса имеет вид

   Видео:✓ Бином Ньютона. Игра в слова. Числа сочетаний | Комбинаторика | Ботай со мной #057 | Борис ТрушинСкачать

   

   Метод Ньютона онлайн

   Данный онлайн калькулятор находит корень уравнения приближённо. В основе алгоритма его работы лежит метод Ньютона. Чтобы начать работу, необходимо ввести исходные данные своей задачи.

   Методом Ньютона, найти корень (

   максимальное кол-во итераций:

   критерий останова вычислений:

   Метод Ньютона является численным, т.е. корень уравнения находится приближенно. При этом можно заранее задать точность его нахождения.

   Пусть нам дано уравнение

   Формула для поиска корня уравнения выглядит следующим образом:

   и — приближённые значения корня уравнения на -ой и ( )-ой итерациях соответственно, — значение функции в точке , — значение производной функции в точке .

   Как видно, для того чтобы начать работу необходимо задать точку — начальное приближение для корня уравнения . От выбора точки зависит сойдётся ли алгоритм к решению или нет. Сходимость метода квадратичная, но она резко ухудшается если мы ищем кратный корень уравнения, т.е. если и одновременно , где — кратный корень уравнения .

   Вычисления по приведённой выше формуле можно продолжать до бесконечности, соответственно на практике необходим некоторый критерий, который будет определять нужно ли нам продолжать вычисления или нет. Как правило, используется критерий останова вычислений на основе приращения или же на основе близости функции к нулю в некоторой точке .

   Критерий останова вычислений на основе приращения задаётся следующей формулой:

   т.е. различие (по модулю) между двумя последовательными приближениями к корню уравнения ( и ) должны быть меньше, некоторой наперёд заданной величины .

   Критерий останова вычислений на основе близости функции к нулю определяется следующей формулой:

   т.е. отличие (по модулю) между функцией в некоторой точке и нулём меньше .

   В тоже время, если последовательность к корню не сходится, то критерии останова не сработают и процесс поиска корня будет продолжаться бесконечно. Чтобы предотвратить такую ситуацию, на практике вычисления прекращают после некоторого, заданного количества итераций.

   На рисунке ниже приведена геометрическая интерпретация процесса поиска корня уравнения методом Ньютона.

   

   В точке мы строим касательную к графику функции . Уравнение касательной в этой точке имеет вид:

   Находим точку пересечения полученной касательной с осью абсцисс, т.е. рассматриваем точку с координатами . Подставляя координаты указанной точки в уравнение касательной, получаем следующее соотношение:

   Из данного уравнения находим :

   Продолжая данный процесс, получим формулу метода Ньютона, приведенную выше. Из-за того, что на каждой итерации фактически происходит построение касательной, метод Ньютона также иногда называют методом касательных.

   Видео:#219. БИНОМ НЬЮТОНА ДЛЯ ЧАЙНИКОВСкачать

   

   Другие полезные разделы:

   Видео:Математика для всех. Алексей Савватеев. Лекция 5.6. Бином НьютонаСкачать

   

   Оставить свой комментарий:

   Мы в социальных сетях:
   Группа ВКонтакте | Бот в Телеграмме

   🌟 Видео

   Урок 11. Бинома Ньютона. Формула общего члена. Алгебра 11 класс.Скачать

   

   Бином Ньютона и треугольник Паскаля | Учитель года Москвы — 2020Скачать

   

   Бином НьютонаСкачать

   

   БИНОМ НЬЮТОНА. Математика для аналитика. Урок №1Скачать

   

   Proje. Бином Ньютона - Объяснение и решение пример.Скачать

   

   Метод Ньютона (метод касательных) Пример РешенияСкачать

   

   Бином НьютонаСкачать

   

   Бином Ньютона - Доказательство по индукцииСкачать

   

   Бином Ньютона — показывает СавватеевСкачать

   

   Доказательство формулы бинома НьютонаСкачать

   

   Бином Ньютона: формула, доказательство и Треугольник ПаскаляСкачать

   

   Бином НьютонаСкачать

   

   11 класс - Алгебра - Бином НьютонаСкачать