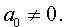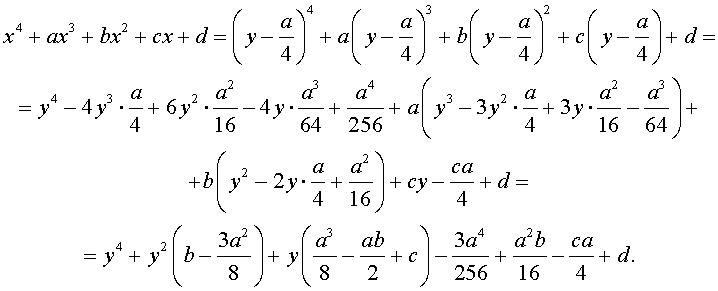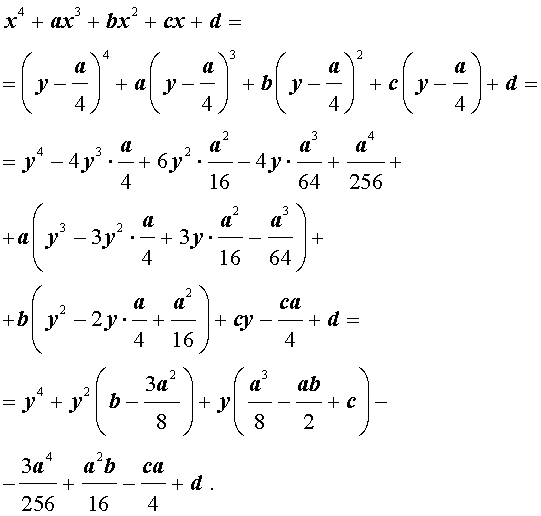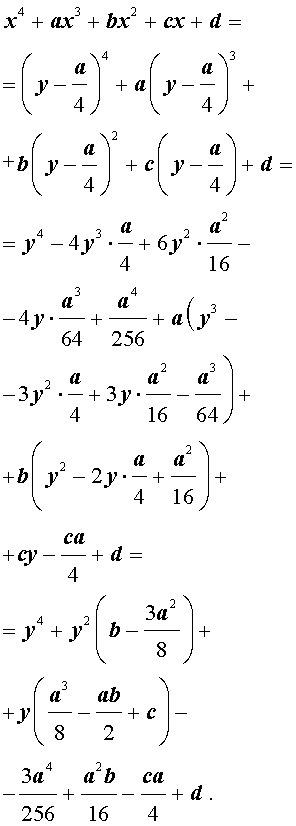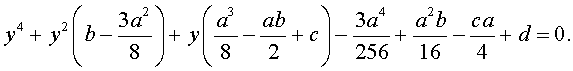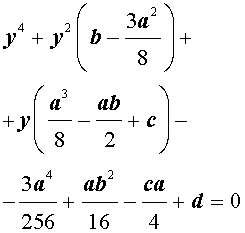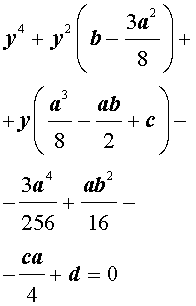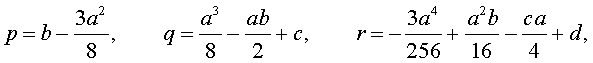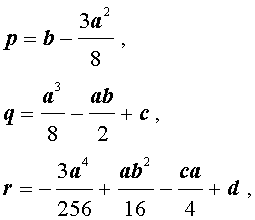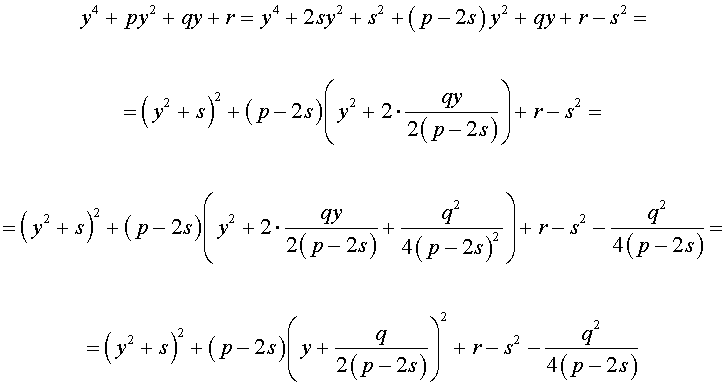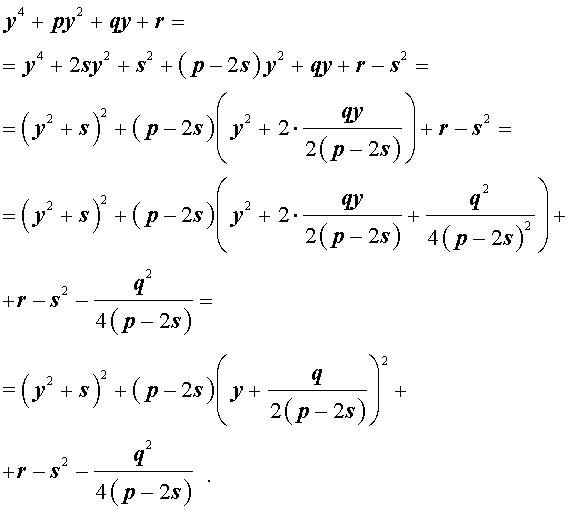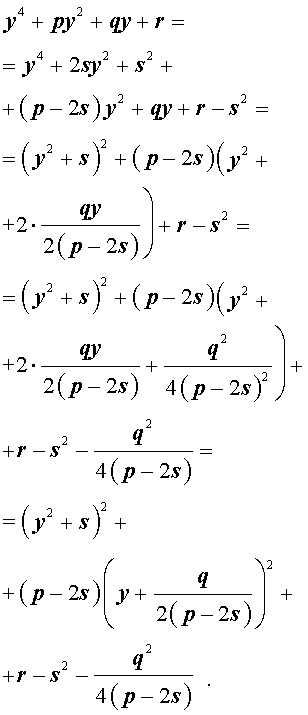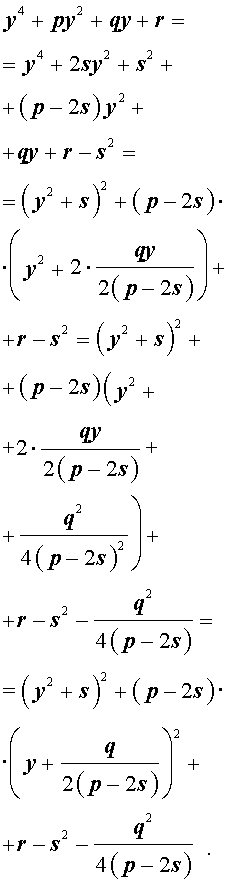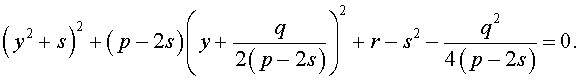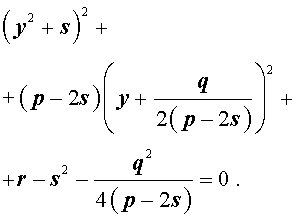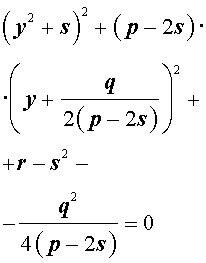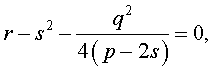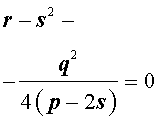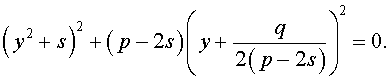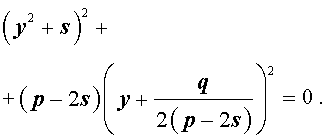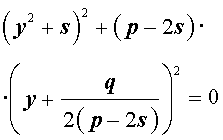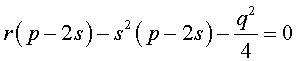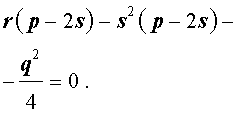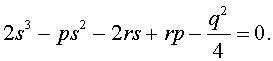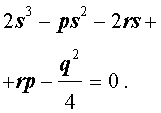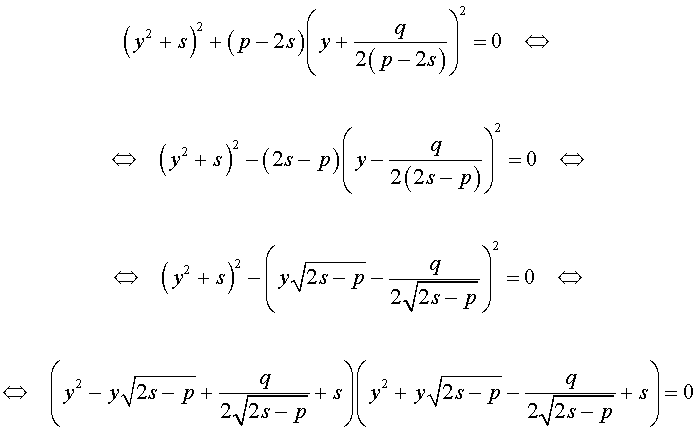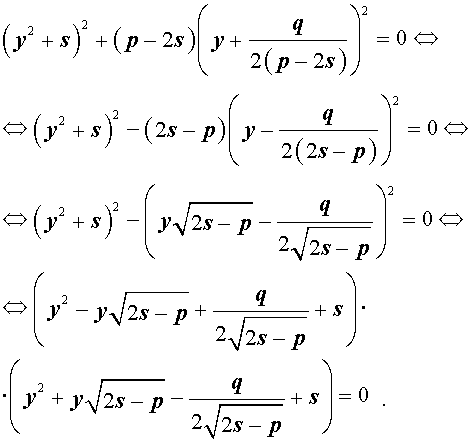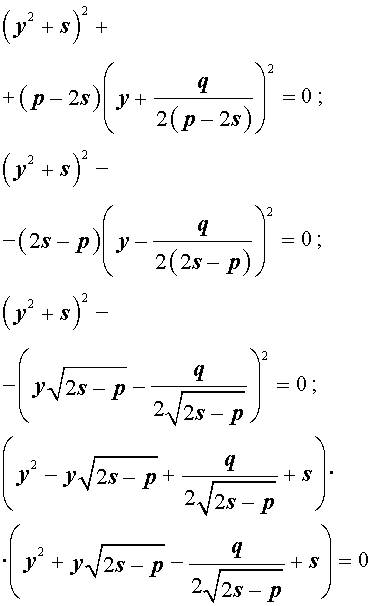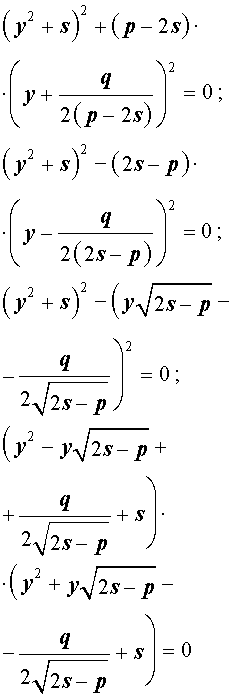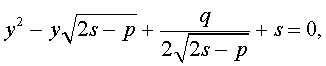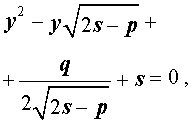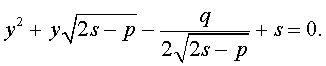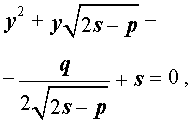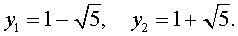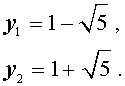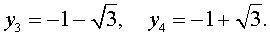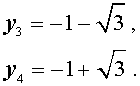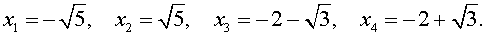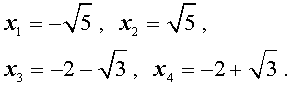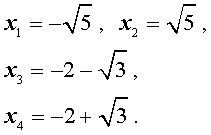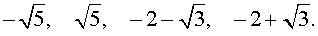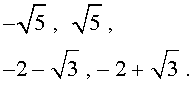Решение уравнения 4 степени разложением на множители (7 видео)

Содержание

Решение уравнений 4-ой степени. Метод Феррари
Схема метода Феррари
Приведение уравнений 4-ой степени
Разложение на множители. Кубическая резольвента
Пример решения уравнения 4-ой степени
Разложение многочлена на множители методом неопределенных коэффициентов
«Решение уравнений высших степеней». 9-й класс
📽️ Видео

Видео:Уравнение четвертой степениСкачать

Решение уравнений 4-ой степени. Метод Феррари

Решение уравнения 4 степени разложением на множители

Схема метода Феррари

Приведение уравнений 4-ой степени

Разложение на множители. Кубическая резольвента

Пример решения уравнения 4-ой степени

Видео:ОГЭ 2022 (Задание 20)Уравнения 4-ой степени, разложение на множителиСкачать

Схема метода Феррари

Целью данного раздела является изложение метода Феррари , с помощью которого можно решать уравнения четвёртой степени

a₀x 4 + a₁x 3 + a₂x 2 +
+ a₃x + a₄ = 0,

(1)

где a₀, a₁, a₂, a₃, a₄ – произвольные вещественные числа, причем

Метод Феррари состоит из двух этапов.

На первом этапе уравнения вида (1) приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного.

На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.

Видео:Как решать уравнения 4 степени Решите уравнение четвертой степени Разложить на множители Безу столбиСкачать

Приведение уравнений 4-ой степени

Разделим уравнение (1) на старший коэффициент a₀ . Тогда оно примет вид

x 4 + ax 3 + bx 2 +
+ cx + d = 0,

(2)

где a, b, c, d – произвольные вещественные числа.

Сделаем в уравнении (2) замену

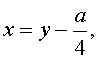(3)

где y – новая переменная.

то уравнение (2) принимает вид

В результате уравнение (2) принимает вид

Если ввести обозначения

то уравнение (4) примет вид

y 4 + py 2 + qy + r = 0,

(5)

где p, q, r – вещественные числа.

Первый этап метода Феррари завершён.

Видео:Разложение кубических выражений на множителиСкачать

Разложение на множители. Кубическая резольвента

Добавив и вычитая в левой части уравнения (5) выражение

где s – некоторое число, которое мы определим чуть позже, из (5) получим

Следовательно, уравнение (5) принимает вид

Если теперь выбрать число s так, чтобы оно являлось каким-нибудь решением уравнения

то уравнение (6) примет вид

Избавляясь от знаменателя, уравнение (7) можно переписать в виде

или, раскрыв скобки, — в виде

Полученное кубическое уравнение (9), эквивалентное уравнению (7), называют кубической резольвентой уравнения 4-ой степени (5).

Если какое-нибудь решение кубической резольвенты (9) найдено, то уравнение (8) можно решить, разложив его левую часть на множители с помощью формулы сокращенного умножения «Разность квадратов».

Таким образом, для решения уравнения (8) остаётся решить квадратное уравнение

а также квадратное уравнение

Вывод метода Феррари завершен.

Видео:Решаем быстро и красиво ★ Уравнение четвертой степени ★ x^4+8x-7=0Скачать

Пример решения уравнения 4-ой степени

Пример . Решить уравнение

x 4 + 4x 3 – 4x 2 –
– 20x – 5 = 0.

(12)

Решение . В соответствии с (3) сделаем в уравнении (12) замену

x = y – 1.

(13)

то в результате замены (13) уравнение (12) принимает вид

y 4 – 10y 2 – 4y + 8 = 0.

(14)

В соответствии с (5) для коэффициентов уравнения (14) справедливы равенства

p = – 10, q = – 4, r = 8.

(15)

В силу (9) и (15) кубической резольвентой для уравнения (14) служит уравнение

которое при сокращении на 2 принимает вид:

s 3 + 5s 2 – 8s – 42 = 0.

(16)

s = – 3.

(17)

Подставляя значения (15) и (17) в формулу (10), получаем уравнение

Подставляя значения (15) и (17) в формулу (11), получаем уравнение

В завершение, воспользовавшись формулой (13), из (18) и (19) находим корни уравнения (12):

Замечание . При решении примера мы попутно получили разложение левой части уравнения (14) на множители:

y 4 – 10y 2 – 4y + 8 =
= (y 2 – 2y – 4) (y 2 +
+ 2y – 2).

(20)

Предоставляем посетителю нашего сайта возможность убедиться в справедливости равенства (19) в качестве несложного упражнения.

Видео:ОГЭ. Задание 21. Уравнение третей степени. Разложение на множители.Скачать

Разложение многочлена на множители методом неопределенных коэффициентов

В этой статье мы рассмотрим решение уравнения четвертой степени с помощью разложения на множители методом неопределенных коэффициентов.

Решить уравнение:

Перед нами уравнение четвертой степени.

Чтобы решить это уравнение, разложим левую часть уравнения на множители.

Многочлен четвертой степени можно разложить на произведение двух многочленов второй степени.

Воспользуемся методом неопределенных коэффициентов.

Пусть выполняется равенство:

Здесь -целые числа.

Перемножим две скобки справа и приведем подобные члены. Получим:

Два многочлена равны тогда и только тогда, когда равны их коэффициенты.

Приравняем коэффициенты при одинаковых степенях и получим систему уравнений:

Без ограничения общности можем считать, что

, тогда пусть

, отсюда или .

Рассмотрим два случая:

Получим систему уравнений:

Из второго и третьего уравнений получаем — что не удовлетворяет третьему уравнению. Система не имеет решений.

2. ,

Из второго и третьего уравнений получаем — и эти значения удовлетворяет третьему уравнению.

Получили:

Тогда наше разложение имеет вид:

Осталось приравнять квадратные трехчлены в скобках к нулю и найти корни:

Ответ: ,

Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

«Решение уравнений высших степеней». 9-й класс

Разделы: Математика

Класс: 9

Учебная:

Углубить знания учащихся по теме “ Решение уравнений высших степеней” и обобщить учебный материал.

Познакомить учащихся с приёмами решения уравнений высших степеней.

Научить учащихся применять теорию делимости при решения уравнений высших степеней.

Научить учащихся выполнять деление “уголком” многочлена на многочлен.

Развивать умения и навыки работы с уравнениями высших степеней.

Развивающая:

Развитие внимания учащихся.
Развитие умения добиваться результатов труда.
Развитие интереса к изучению алгебры и навыков самостоятельной работы.

Воспитывающая:

Воспитание чувства коллективизма.

Формирование чувства ответственности за результат работы.

Формирование у учащихся адекватной самооценки при выборе отметки за работу на уроке.

Оборудование: компьютер, проектор.

1 этап работы. Организационный момент.

2 этап работы. Мотивация и выход на постановку проблемы

Уравнение одно из важнейших понятий математики. Развитие методов решения уравнений, начиная с зарождения математики как науки, долгое время было основным предметом изучения алгебры.

В школьном курсе изучения математики очень много внимания уделяется решению различного вида уравнений. До девятого класса мы умели решать только линейные и квадратные уравнения. Уравнения третьей, четвёртой и т.д. степеней называются уравнениями высших степеней. В девятом классе мы познакомились с двумя основными приёмами решения некоторых уравнений третьей и четвёртой степеней: разложение многочлена на множители и использование замены переменной.

А можно ли решить уравнения более высоких степеней? На этот вопрос мы постараемся сегодня найти ответ.

3 этап работы. Повторить ранее изученный материал. Ввести понятие уравнения высших степеней.

1) Решение линейного уравнения.

Линейным называется уравнение вида , где по определению. Такое уравнение имеет единственный корень .

2) Решение квадратного уравнения.

Квадратным называется уравнение вида , где . Количество корней и сами корни определяются дискриминантом уравнения . Для уравнение корней не имеет, для имеет один корень (два одинаковых корня)

, для имеет два различных корня .

Из рассмотренных линейных и квадратных уравнений видим, что количество корней уравнения не более его степени. В курсе высшей алгебры доказывается, что уравнение -й степени имеет не более n корней. Что касается самих корней, то тут ситуация намного сложнее. Для уравнений третьей и четвёртой степеней известны формулы для нахождения корней. Однако эти формулы очень сложны и громоздки и практического применения не имеют. Для уравнений пятой и более высоких степеней общих формул не существует и существовать не может (как было доказано в XIX в. Н. Абелем и Э. Галуа).

Будем называть уравнения третьей, четвёртой и т.д. степеней уравнениями высших степеней. Некоторые уравнения высоких степеней удаётся решить с помощью двух основных приёмов: разложением многочлена на множители или с использованием замены переменной.

3) Решение кубического уравнения.

Решим кубическое уравнение

Сгруппируем члены многочлена, стоящего в левой части уравнения, и разложим на множители. Получим:

Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три линейных уравнения:

Итак, данное кубическое уравнение имеет три корня: ; ;.

4) Решение биквадратного уравнения.

Очень распространены биквадратные уравнения, которые имеют вид (т.е. уравнения, квадратные относительно ). Для их решения вводят новую переменную .

Решим биквадратное уравнение .

Введём новую переменную и получим квадратное уравнение , корнями которого являются числа и 4.

Вернёмся к старой переменной и получим два простейших квадратных уравнения:

(корни и )

Итак, данное биквадратное уравнение имеет четыре корня:

; ;.

Попробуем решить уравнение используя выше изложенные приёмы.

4 этап работы. Привести некоторые утверждения о корнях многочлена вида , где многочлен n-й степени

Приведём некоторые утверждения о корнях многочлена вида :

1) Многочлен -й степени имеет не более корней (с учётом их кратностей). Например, многочлен третьей степени не может иметь четыре корня.

2) Многочлен нечётной степени имеет хотя бы один корень. Например, многочлены первой, третьей, пятой и т.д. степени имеют хотя бы один корень. Многочлены чётной степени корней могут и не иметь.

3) Если на концах отрезка значения многочлена имеют разные знаки (т.е. ,), то на интервале находится хотя бы один корень. Это утверждение широко используется для приближенного вычисления корней многочлена.

4) Если число является корнем многочлена вида , то этот многочлен можно представить в виде произведения , где многочлен (-й степени. Другими словами, многочлена вида можно разделить без остатка на двучлен . Это позволяет уравнение -й степени сводить к уравнению (-й степени (понижать степень уравнения).

5) Если уравнение со всеми целыми коэффициентами (причём свободный член ) имеет целый корень , то этот корень является делителем свободного члена . Такое утверждение позволяет подобрать целый корень многочлена (если он есть).

5 этап работы. Показать как применяется теория делимости для решения уравнений высших степеней. Рассмотреть примеры решения уравнений высших степеней , в которых для разложения левой части на множители используется способ деления многочлена на многочлен “уголком”.

Пример 1. Решим уравнение .

Если это уравнение имеет целый корень, то он является делителем свободного члена (-1), т.е. равняется одному из чисел: . Проверка показывает, что корнем уравнения является число -1. Значит, многочлен можно представить в виде произведения , т.е. многочлен можно без остатка разделить на двучлен . Выполним такое деление “уголком”:

Таким образом, мы фактически разложили левую часть уравнения на множители:

Произведение множителей равно нулю, если один из множителей равен нулю. Получаем два уравнения:

Итак, данное уравнение имеет три корня:

Пример 2. Решим уравнение .

Если это уравнение имеет целый корень, то он является делителем свободного члена (9),т.е. равняется одному из чисел: ;. Проверим:

Значит, многочлен можно представить в виде произведения , т.е. многочлен можно без остатка разделить на двучлен . Выполним такое деление “уголком”:

Таким образом, мы разложили левую часть уравнения на множители:

Аналогичным образом поступим и с многочленом .

Если это уравнение имеет целый корень, то он является делителем свободного члена (9), т.е. равняется одному из чисел: ;. Проверим:

Значит, многочлен можно представить в виде

произведения , т.е. многочлен можно без остатка разделить на двучлен . Выполним такое деление “уголком”:

Таким образом, мы разложили левую часть исходного уравнения на множители:

Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три уравнения:

Итак, данное уравнение имеет четыре корня:

6 этап работы. Закрепление изученного материала.

Решите уравнения высших степеней, используя способ деления многочлена на многочлен “уголком”.

7 этап работы. Вывод урока.

Решить уравнения высших степеней можно следующим образом:

используя формулы для нахождения корней (если они известны);
используя замену переменной;
раскладывая многочлен в левой части уравнения на множители, используя способ деления многочлена на многочлен “уголком”.

8 этап работы. Домашнее задание.

Дома решить уравнения высших степеней, используя способ деления многочлена на многочлен “уголком” (раздать листы с заданиями).