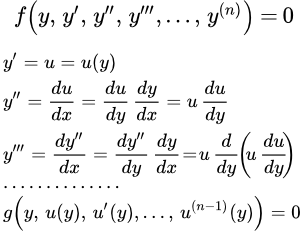Решение уравнений второго порядка не содержащих явной зависимости от неизвестной функции

Видео:ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Метод решения

Рассмотрим уравнение, не содержащее независимую переменную в явном виде:
(1) .
Порядок этого уравнения понижается на единицу с помощью подстановки:

Далее считаем, что функция u зависит от переменной y , тогда:
;
;
и т. д.

В результате такой подстановки, порядок уравнения понижается на единицу.

Видео:14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Пример

Уравнение не содержит независимую переменную в явном виде. Делаем подстановку:
.
Считаем, что функция u зависит от переменной y . Тогда
.

Подставляем в исходное уравнение:
.
Делим на u . При имеем:
.
Это уравнение с разделяющимися переменными. Делим на и умножаем на dy . При имеем:
.
Интегрируем:
(2) .

Подставляем в (2):
.
Потенцируем:
.
Заменим постоянную интегрирования . Знак модуля сводится к умножению на ±1 . Включим ±1 в постоянную . То есть мы теперь полагаем, что может быть не только положительным, но и отрицательным числом. Тогда:
.

Выполняем преобразования:
;
.
При имеем:
;
.

Разделяем переменные:
.
Интегрируем:
(3) .

Вычисляем интеграл:

.
Подставляем в (3):
;
.
Возводим в квадрат и выполняем преобразования:
;
;
(4) .

При выводе формулы (4) мы предполагали, что
и .
Теперь рассмотрим случаи
.
Нетрудно видеть, что решение, охватывающее эти три равенства, есть
(5) ,
где C – произвольная постоянная. Тогда . Подставляя это в исходное уравнение нетрудно убедиться, что оно выполняется. Это особое решение. Добавим его в ответ.

Автор: Олег Одинцов . Опубликовано: 18-07-2013 Изменено: 27-06-2018

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Данная статья раскрывает вопрос о решении линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами. Будет рассмотрена теория вместе с примерами приведенных задач. Для расшифровки непонятных терминов необходимо обращаться к теме об основных определениях и понятиях теории дифференциальных уравнений.

Рассмотрим линейное дифференциальное уравнение (ЛНДУ) второго порядка с постоянными коэффициентами вида y » + p · y ‘ + q · y = f ( x ) , где произвольными числами являются p и q , а имеющаяся функция f ( х ) непрерывная на интервале интегрирования x .

Перейдем к формулировке теоремы общего решения ЛНДУ.

Видео:Дифференциальные уравнения высших порядков, допускающие понижение порядкаСкачать

Теорема общего решения ЛДНУ

Общим решением, находящимся на интервале х , неоднородного дифференциального уравнения вида y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 0 ( x ) · y = f ( x ) с непрерывными коэффициентами интегрирования на x интервале f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) и непрерывной функцией f ( x ) равняется сумме общего решения y 0 , которое соответствует ЛОДУ и каким-нибудь частным решением y

, где исходным неоднородным уравнением является y = y 0 + y

Отсюда видно, что решение такого уравнения второго порядка имеет вид y = y 0 + y

. Алгоритм нахождения y 0 рассмотрен в статье о линейных однородных дифференциальных уравнениях второго порядка с постоянными коэффициентами. После чего следует переходить к определению y

Выбор частного решения ЛНДУ зависит от вида имеющейся функции f ( x ) , располагающейся в правой части уравнения. Для этого необходимо рассмотреть отдельно решения линейных неоднородных дифференциальных уравнений второго порядка при постоянных коэффициентах.

Когда f ( x ) считается за многочлен n -ой степени f ( x ) = P n ( x ) , отсюда следует, что частное решение ЛНДУ находим по формуле вида y

= Q n ( x ) · x γ , где Q n ( x ) является многочленом степени n , r – это количество нулевых корней характеристического уравнения. Значение y

является частным решением y

= f ( x ) , тогда имеющиеся коэффициенты, которые определены многочленом
Q n ( x ) , отыскиваем при помощи метода неопределенных коэффициентов из равенства y

Вычислить по теореме Коши y » — 2 y ‘ = x 2 + 1 , y ( 0 ) = 2 , y ‘ ( 0 ) = 1 4 .

Решение

Иначе говоря, необходимо перейти к частному решению линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами y » — 2 y ‘ = x 2 + 1 , которое будет удовлетворять заданным условиям y ( 0 ) = 2 , y ‘ ( 0 ) = 1 4 .

Общим решением линейного неоднородного уравнения является сумма общего решения, которое соответствует уравнению y 0 или частному решению неоднородного уравнения y

, то есть y = y 0 + y

Для начала найдем общее решение для ЛНДУ, а после чего – частное.

Перейдем к нахождению y 0 . Запись характеристического уравнения поможет найти корни. Получаем, что

k 2 — 2 k = 0 k ( k — 2 ) = 0 k 1 = 0 , k 2 = 2

Получили, что корни различные и действительные. Поэтому запишем

y 0 = C 1 e 0 x + C 2 e 2 x = C 1 + C 2 e 2 x .

. Видно, что правая часть заданного уравнения является многочленом второй степени, тогда один из корней равняется нулю. Отсюда получим, что частным решением для y

= Q 2 ( x ) · x γ = ( A x 2 + B x + C ) · x = A x 3 + B x 2 + C x , где значения А , В , С принимают неопределенные коэффициенты.

Найдем их из равенства вида y

Тогда получим, что:

‘ = x 2 + 1 ( A x 3 + B x 2 + C x ) » — 2 ( A x 3 + B x 2 + C x ) ‘ = x 2 + 1 3 A x 2 + 2 B x + C ‘ — 6 A x 2 — 4 B x — 2 C = x 2 + 1 6 A x + 2 B — 6 A x 2 — 4 B x — 2 C = x 2 + 1 — 6 A x 2 + x ( 6 A — 4 B ) + 2 B — 2 C = x 2 + 1

Приравняв коэффициенты с одинаковыми показателями степеней x , получим систему линейных выражений — 6 A = 1 6 A — 4 B = 0 2 B — 2 C = 1 . При решении любым из способов найдем коэффициенты и запишем: A = — 1 6 , B = — 1 4 , C = — 3 4 и y

= A x 3 + B x 2 + C x = — 1 6 x 3 — 1 4 x 2 — 3 4 x .

Эта запись называется общим решением исходного линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.

Для нахождения частного решения, которое удовлетворяет условиям y ( 0 ) = 2 , y ‘ ( 0 ) = 1 4 , требуется определить значения C 1 и C 2 , исходя из равенства вида y = C 1 + C 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x .

y ( 0 ) = C 1 + C 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x x = 0 = C 1 + C 2 y ‘ ( 0 ) = C 1 + C 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x ‘ x = 0 = = 2 C 2 e 2 x — 1 2 x 2 + 1 2 x + 3 4 x = 0 = 2 C 2 — 3 4

Работаем с полученной системой уравнений вида C 1 + C 2 = 2 2 C 2 — 3 4 = 1 4 , где C 1 = 3 2 , C 2 = 1 2 .

Применив теорему Коши, имеем, что

y = C 1 + C 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x = = 3 2 + 1 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x

Ответ: 3 2 + 1 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x .

Когда функция f ( x ) представляется в виде произведения многочлена со степенью n и экспоненты f ( x ) = P n ( x ) · e a x , тогда отсюда получаем, что частным решением ЛНДУ второго порядка будет уравнение вида y

= e a x · Q n ( x ) · x γ , где Q n ( x ) является многочленом n -ой степени, а r – количеством корней характеристического уравнения, равняющиеся α .

Коэффициенты, принадлежащие Q n ( x ) находятся по равенству y

Найти общее решение дифференциального уравнения вида y » — 2 y ‘ = ( x 2 + 1 ) · e x .

Решение

Уравнение общего вида y = y 0 + y

. Указанное уравнение соответствует ЛОДУ y » — 2 y ‘ = 0 . По предыдущему примеру видно, что его корни равняются k 1 = 0 и k 2 = 2 и y 0 = C 1 + C 2 e 2 x по характеристическому уравнению.

Видно, что правой частью уравнения является x 2 + 1 · e x . Отсюда ЛНДУ находится через y

= e a x · Q n ( x ) · x γ , где Q n ( x ) , являющимся многочленом второй степени, где α = 1 и r = 0 , потому как у характеристического уравнения отсутствует корень, равный 1 . Отсюда получаем, что

= e a x · Q n ( x ) · x γ = e x · A x 2 + B x + C · x 0 = e x · A x 2 + B x + C .

А , В , С являются неизвестными коэффициентами, которые можно найти по равенству y

‘ = e x · A x 2 + B x + C ‘ = e x · A x 2 + B x + C + e x · 2 A x + B = = e x · A x 2 + x 2 A + B + B + C y

‘ ‘ = e x · A x 2 + x 2 A + B + B + C ‘ = = e x · A x 2 + x 2 A + B + B + C + e x · 2 A x + 2 A + B = = e x · A x 2 + x 4 A + B + 2 A + 2 B + C

‘ = ( x 2 + 1 ) · e x ⇔ e x · A x 2 + x 4 A + B + 2 A + 2 B + C — — 2 e x · A x 2 + x 2 A + B + B + C = x 2 + 1 · e x ⇔ e x · — A x 2 — B x + 2 A — C = ( x 2 + 1 ) · e x ⇔ — A x 2 — B x + 2 A — C = x 2 + 1 ⇔ — A x 2 — B x + 2 A — C = 1 · x 2 + 0 · x + 1

Показатели при одинаковых коэффициентах приравниваем и получаем систему линейных уравнений. Отсюда и находим А , В , С :

— A = 1 — B = 0 2 A — C = 1 ⇔ A = — 1 B = 0 C = — 3

Ответ: видно, что y

= e x · ( A x 2 + B x + C ) = e x · — x 2 + 0 · x — 3 = — e x · x 2 + 3 является частным решением ЛНДУ, а y = y 0 + y = C 1 e 2 x — e x · x 2 + 3 — общим решением для неоднородного дифуравнения второго порядка.

Когда функция записывается как f ( x ) = A 1 cos ( β x ) + B 1 sin β x , а А 1 и В 1 являются числами, тогда частным решением ЛНДУ считается уравнение вида y

= A cos β x + B sin β x · x γ , где А и В считаются неопределенными коэффициентами, а r числом комплексно сопряженных корней, относящихся к характеристическому уравнению, равняющимся ± i β . В этом случае поиск коэффициентов проводится по равенству y

Найти общее решение дифференциального уравнения вида y » + 4 y = cos ( 2 x ) + 3 sin ( 2 x ) .

Решение

Перед написанием характеристического уравнения находим y 0 . Тогда

k 2 + 4 = 0 k 2 = — 4 k 1 = 2 i , k 2 = — 2 i

Имеем пару комплексно сопряженных корней. Преобразуем и получим:

y 0 = e 0 · ( C 1 cos ( 2 x ) + C 2 sin ( 2 x ) ) = C 1 cos 2 x + C 2 sin ( 2 x )

Корни из характеристического уравнения считаются сопряженной парой ± 2 i , тогда f ( x ) = cos ( 2 x ) + 3 sin ( 2 x ) . Отсюда видно, что поиск y

будет производиться из y

= ( A cos ( β x ) + B sin ( β x ) · x γ = ( A cos ( 2 x ) + B sin ( 2 x ) ) · x . Неизвестные коэффициенты А и В будем искать из равенства вида y

= cos ( 2 x ) + 3 sin ( 2 x ) .

‘ = ( ( A cos ( 2 x ) + B sin ( 2 x ) · x ) ‘ = = ( — 2 A sin ( 2 x ) + 2 B cos ( 2 x ) ) · x + A cos ( 2 x ) + B sin ( 2 x ) y

» = ( ( — 2 A sin ( 2 x ) + 2 B cos ( 2 x ) ) · x + A cos ( 2 x ) + B sin ( 2 x ) ) ‘ = = ( — 4 A cos ( 2 x ) — 4 B sin ( 2 x ) ) · x — 2 A sin ( 2 x ) + 2 B cos ( 2 x ) — — 2 A sin ( 2 x ) + 2 B cos ( 2 x ) = = ( — 4 A cos ( 2 x ) — 4 B sin ( 2 x ) ) · x — 4 A sin ( 2 x ) + 4 B cos ( 2 x )

Тогда видно, что

= cos ( 2 x ) + 3 sin ( 2 x ) ⇔ ( — 4 A cos ( 2 x ) — 4 B sin ( 2 x ) ) · x — 4 A sin ( 2 x ) + 4 B cos ( 2 x ) + + 4 ( A cos ( 2 x ) + B sin ( 2 x ) ) · x = cos ( 2 x ) + 3 sin ( 2 x ) ⇔ — 4 A sin ( 2 x ) + 4 B cos ( 2 x ) = cos ( 2 x ) + 3 sin ( 2 x )

Необходимо приравнять коэффициенты синусов и косинусов. Получаем систему вида:

— 4 A = 3 4 B = 1 ⇔ A = — 3 4 B = 1 4

= ( A cos ( 2 x ) + B sin ( 2 x ) · x = — 3 4 cos ( 2 x ) + 1 4 sin ( 2 x ) · x .

Ответ: общим решением исходного ЛНДУ второго порядка с постоянными коэффициентами считается

= = C 1 cos ( 2 x ) + C 2 sin ( 2 x ) + — 3 4 cos ( 2 x ) + 1 4 sin ( 2 x ) · x

Когда f ( x ) = e a x · P n ( x ) sin ( β x ) + Q k ( x ) cos ( β x ) , тогда y

= e a x · ( L m ( x ) sin ( β x ) + N m ( x ) cos ( β x ) · x γ . Имеем, что r – это число комплексно сопряженных пар корней, относящихся к характеристическому уравнению, равняются α ± i β , где P n ( x ) , Q k ( x ) , L m ( x ) и N m ( x ) являются многочленами степени n , k , т , m , где m = m a x ( n , k ) . Нахождение коэффициентов L m ( x ) и N m ( x ) производится, исходя из равенства y

Найти общее решение y » + 3 y ‘ + 2 y = — e 3 x · ( ( 38 x + 45 ) sin ( 5 x ) + ( 8 x — 5 ) cos ( 5 x ) ) .

Решение

По условию видно, что

α = 3 , β = 5 , P n ( x ) = — 38 x — 45 , Q k ( x ) = — 8 x + 5 , n = 1 , k = 1

Тогда m = m a x ( n , k ) = 1 . Производим нахождение y 0 , предварительно записав характеристическое уравнение вида:

k 2 — 3 k + 2 = 0 D = 3 2 — 4 · 1 · 2 = 1 k 1 = 3 — 1 2 = 1 , k 2 = 3 + 1 2 = 2

Получили, что корни являются действительными и различными. Отсюда y 0 = C 1 e x + C 2 e 2 x . Далее необходимо искать общее решение, исходя из неоднородного уравнения y

= e α x · ( L m ( x ) sin ( β x ) + N m ( x ) cos ( β x ) · x γ = = e 3 x · ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) · x 0 = = e 3 x · ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) )

Известно, что А , В , С являются коэффициентами, r = 0 , потому как отсутствует пара сопряженных корней, относящихся к характеристическому уравнению с α ± i β = 3 ± 5 · i . Данные коэффициенты находим из полученного равенства:

= — e 3 x ( ( 38 x + 45 ) sin ( 5 x ) + ( 8 x — 5 ) cos ( 5 x ) ) ⇔ ( e 3 x ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) ) » — — 3 ( e 3 x ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) ) = — e 3 x ( ( 38 x + 45 ) sin ( 5 x ) + ( 8 x — 5 ) cos ( 5 x ) )

Нахождение производной и подобных слагаемых дает

— e 3 x · ( ( 15 A + 23 C ) · x · sin ( 5 x ) + + ( 10 A + 15 B — 3 C + 23 D ) · sin ( 5 x ) + + ( 23 A — 15 C ) · x · cos ( 5 x ) + ( — 3 A + 23 B — 10 C — 15 D ) · cos ( 5 x ) ) = = — e 3 x · ( 38 · x · sin ( 5 x ) + 45 · sin ( 5 x ) + + 8 · x · cos ( 5 x ) — 5 · cos ( 5 x ) )

После приравнивания коэффициентов получаем систему вида

15 A + 23 C = 38 10 A + 15 B — 3 C + 23 D = 45 23 A — 15 C = 8 — 3 A + 23 B — 10 C — 15 D = — 5 ⇔ A = 1 B = 1 C = 1 D = 1

Из всего следует, что

= e 3 x · ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) = = e 3 x · ( ( x + 1 ) cos ( 5 x ) + ( x + 1 ) sin ( 5 x ) )

Ответ: теперь получено общее решение заданного линейного уравнения:

= = C 1 e x + C 2 e 2 x + e 3 x · ( ( x + 1 ) cos ( 5 x ) + ( x + 1 ) sin ( 5 x ) )

Видео:Дифференциальные уравнения, не содержащие явно независимой переменной (часть 3). Высшая математика.Скачать

Алгоритм решения ЛДНУ

Любой другой вид функции f ( x ) для решения предусматривает соблюдение алгоритма решения:

• нахождение общего решения соответствующего линейного однородного уравнения, где y 0 = C 1 ⋅ y 1 + C 2 ⋅ y 2 , где y 1 и y 2 являются линейно независимыми частными решениями ЛОДУ, С 1 и С 2 считаются произвольными постоянными;
• принятие в качестве общего решения ЛНДУ y = C 1 ( x ) ⋅ y 1 + C 2 ( x ) ⋅ y 2 ;
• определение производных функции через систему вида C 1 ‘ ( x ) + y 1 ( x ) + C 2 ‘ ( x ) · y 2 ( x ) = 0 C 1 ‘ ( x ) + y 1 ‘ ( x ) + C 2 ‘ ( x ) · y 2 ‘ ( x ) = f ( x ) , а нахождение функций C 1 ( x ) и C 2 ( x ) посредствам интегрирования.

Найти общее решение для y » + 36 y = 24 sin ( 6 x ) — 12 cos ( 6 x ) + 36 e 6 x .

Решение

Переходим к написанию характеристического уравнения, предварительно записав y 0 , y » + 36 y = 0 . Запишем и решим:

k 2 + 36 = 0 k 1 = 6 i , k 2 = — 6 i ⇒ y 0 = C 1 cos ( 6 x ) + C 2 sin ( 6 x ) ⇒ y 1 ( x ) = cos ( 6 x ) , y 2 ( x ) = sin ( 6 x )

Имеем, что запись общего решения заданного уравнения получит вид y = C 1 ( x ) · cos ( 6 x ) + C 2 ( x ) · sin ( 6 x ) . Необходимо перейти к определению производных функций C 1 ( x ) и C 2 ( x ) по системе с уравнениями:

C 1 ‘ ( x ) · cos ( 6 x ) + C 2 ‘ ( x ) · sin ( 6 x ) = 0 C 1 ‘ ( x ) · ( cos ( 6 x ) ) ‘ + C 2 ‘ ( x ) · ( sin ( 6 x ) ) ‘ = 0 ⇔ C 1 ‘ ( x ) · cos ( 6 x ) + C 2 ‘ ( x ) · sin ( 6 x ) = 0 C 1 ‘ ( x ) ( — 6 sin ( 6 x ) + C 2 ‘ ( x ) ( 6 cos ( 6 x ) ) = = 24 sin ( 6 x ) — 12 cos ( 6 x ) + 36 e 6 x

Необходимо произвести решение относительно C 1 ‘ ( x ) и C 2 ‘ ( x ) при помощи любого способа. Тогда запишем:

C 1 ‘ ( x ) = — 4 sin 2 ( 6 x ) + 2 sin ( 6 x ) cos ( 6 x ) — 6 e 6 x sin ( 6 x ) C 2 ‘ ( x ) = 4 sin ( 6 x ) cos ( 6 x ) — 2 cos 2 ( 6 x ) + 6 e 6 x cos ( 6 x )

Каждое из уравнений следует проинтегрировать . Тогда запишем получившиеся уравнения:

C 1 ( x ) = 1 3 sin ( 6 x ) cos ( 6 x ) — 2 x — 1 6 cos 2 ( 6 x ) + + 1 2 e 6 x cos ( 6 x ) — 1 2 e 6 x sin ( 6 x ) + C 3 C 2 ( x ) = — 1 6 sin ( 6 x ) cos ( 6 x ) — x — 1 3 cos 2 ( 6 x ) + + 1 2 e 6 x cos ( 6 x ) + 1 2 e 6 x sin ( 6 x ) + C 4

Отсюда следует, что общее решение будет иметь вид:

y = 1 3 sin ( 6 x ) cos ( 6 x ) — 2 x — 1 6 cos 2 ( 6 x ) + + 1 2 e 6 x cos ( 6 x ) — 1 2 e 6 x sin ( 6 x ) + C 3 · cos ( 6 x ) + + — 1 6 sin ( 6 x ) cos ( 6 x ) — x — 1 3 cos 2 ( 6 x ) + + 1 2 e 6 x cos ( 6 x ) + 1 2 e 6 x sin ( 6 x ) + C 4 · sin ( 6 x ) = = — 2 x · cos ( 6 x ) — x · sin ( 6 x ) — 1 6 cos ( 6 x ) + + 1 2 e 6 x + C 3 · cos ( 6 x ) + C 4 · sin ( 6 x )

Ответ: y = y 0 + y

= — 2 x · cos ( 6 x ) — x · sin ( 6 x ) — 1 6 cos ( 6 x ) + + 1 2 e 6 x + C 3 · cos ( 6 x ) + C 4 · sin ( 6 x )

Видео:ДУ высших порядков, не содержащие независимую переменную.Скачать

Дифференциальные уравнения, приводимые к уравнениям первого порядка

Вы будете перенаправлены на Автор24

Видео:Дифференциальные уравнения, не содержащие явно независимой переменной (часть 1). Высшая математика.Скачать

Дифференциальные уравнения второго порядка, в которых правая часть не зависит от неизвестной функции и её производной

Таким дифференциальным уравнением второго порядка является уравнение вида $y»=fleft(xright)$. В нем правая часть не зависит от неизвестной функции $y$ и её производной $y’$, а зависит только от $x$. Решается это уравнение последовательным интегрированием.

Представим его в таком виде: $frac left(y’right)=fleft(xright)$, откуда $dleft(y’right)=fleft(xright)cdot dx$.

Интегрируем первый раз, используя то свойство, что неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: $int dleft(y’right) =int fleft(xright)cdot dx $ или $y’=int fleft(xright)cdot dx +C_ $, где $C_ $ — произвольная постоянная.

Таким образом, дифференциальное уравнение второго порядка сведено теперь к дифференциальному уравнению первого порядка, которое можно представить в таком виде: $dy=left(int fleft(xright)cdot dx +C_ right)cdot dx$.

Интегрируем полученное дифференциальное уравнение повторно: $y=int left(int fleft(xright)cdot dx +C_ right)cdot dx =int left(int fleft(xright)cdot dx right)cdot dx +int C_ cdot dx$. Окончательно получаем:$y=int left(int fleft(xright)cdot dx right)cdot dx +C_ cdot x+C_ $, где $C_ $ — произвольная постоянная.

Процесс интегрирования завершен. Получена неизвестная функция $y$, которая является общим решением данного дифференциального уравнения второго порядка.

Алгоритм решения дифференциального уравнения второго порядка $y»=fleft(xright)$ может быть представлен в следующем виде:

1. находим интеграл $I_ left(xright)=int fleft(xright)cdot dx $ и записываем первую производную искомой функции в виде $y’left(x,C_ right)=I_ left(xright)+C_ $;
2. находим интеграл $I_ left(xright)=int I_ left(xright)cdot dx $ и записываем окончательно общее решение данного дифференциального уравнения: $y=I_ left(xright)+C_ cdot x+C_ $;
3. для поиска частного решения начальные условия подставляем в выражение для первой производной $y’$, а также в общее решение; в результате находим значения произвольных постоянных $C_ $ и $C_ $.

Готовые работы на аналогичную тему

Найти общее решение дифференциального уравнения второго порядка $y»=4$. Записать также его частное решение, которое удовлетворяет начальным условиям $y=1$ при $x=1$, $y’=1$ при $x=1$.

В данном дифференциальном уравнении правая часть не зависит ни от неизвестной функции $y$, ни от её производной $y’$. Следовательно, оно решается последовательным интегрированием два раза подряд.

Находим интеграл $I_ left(xright)=int fleft(xright)cdot dx =int 4cdot dx =4cdot x$. Записываем выражение для первой производной в виде $y’left(x,C_ right)=I_ left(xright)+C_ $, то есть $y’=4cdot x+C_ $.

Находим интеграл $I_ left(xright)=int I_ left(xright)cdot dx =int 4cdot xcdot dx =2cdot x^ $. Записываем окончательно общее решение в виде $y=I_ left(xright)+C_ cdot x+C_ $. Получаем: $y=2cdot x^ +C_ cdot x+C_ $.

Ищем частное решение. Подставляем начальное условие $y’=1$ при $x=1$ в выражение для $y’$: $1=4cdot 1+C_ $, откуда $C_ =-3$. Подставляем начальное условие $y=1$ при $x=1$ в выражение для $y$: $1=2cdot 1^ +left(-3right)cdot 1+C_ $, откуда $C_ =2$. Таким образом, частное решение имеет вид: $y=2cdot x^ -3cdot x+2$.

Видео:Дифференциальные уравнения, не содержащие явно искомой функции (часть 2). Высшая математика.Скачать

Дифференциальные уравнения второго порядка, не содержащие неизвестной функции

Указанные дифференциальные уравнения второго порядка допускают понижение порядка посредством замены переменных. После этого к полученным дифференциальным уравнениям первого порядка могут быть применены известные методы решения.

Дифференциальное уравнение второго порядка, не содержащее неизвестной функции $y$, имеет вид $y»=fleft(x,y’right)$.

Для его решения применяют замену $y’=zleft(xright)$.

При этом $y»=z’left(xright)$. После подстановки данное дифференциальное уравнение приобретает вид дифференциального уравнения первого порядка относительно $z$, то есть $z’=fleft(x,zright)$. Решая его, находим $zleft(xright)=phi left(x,C_ right)$.

В свою очередь, поскольку $y’=zleft(xright)$, то $y’=phi left(x,C_ right)$. Это также дифференциальное уравнение первого порядка, которое допускает непосредственное интегрирование. Следовательно, интегрируя еще раз, окончательно получаем общее решение $y=int phi left(x,C_ right)cdot dx +C_ $.

Алгоритм решения дифференциального уравнения второго порядка $y»=fleft(x,y’right)$ может быть представлен в следующем виде:

1. переписываем данное дифференциальное уравнение в виде дифференциального уравнения первого порядка относительно переменной $z$, формально заменив $y»$ на $z’$, а $y’$ — на $z$;
2. полученное дифференциальное уравнение первого порядка решаем одним из подходящих известных методов;
3. найденное решение $z=phi left(x,C_ right)$ представляем в виде дифференциального уравнения первого порядка $y’=phi left(x,C_ right)$, которое допускает непосредственное интегрирование;
4. находим интеграл $I=int phi left(x,C_ right)cdot dx $ и получаем общее решение в виде $y=I+C_ $.

Найти общее решение дифференциального уравнения$y»-frac =3cdot x$.

Данное дифференциальное уравнение не содержит неизвестной функции $y$, поэтому переписываем его в виде дифференциального уравнения первого порядка относительно переменной $z$, формально заменив $y»$ на $z’$, а $y’$ — на $z$. Получаем: $z’-frac =3cdot x$.

Это дифференциальное уравнение первого порядка является линейным неоднородным, решая которое известным методом, получаем $z=left(3cdot x+C_ right)cdot x$.

Найденное решение представляем в виде дифференциального уравнения первого порядка $y’=phi left(x,C_ right)$, то есть $y’=left(3cdot x+C_ right)cdot x$. Это дифференциальное уравнение допускает непосредственное интегрирование.

Находим интеграл $I=int phi left(x,C_ right)cdot dx =int left(3cdot x+C_ right)cdot xcdot dx =x^ +C_ cdot frac <x^> $ и получаем общее решение в виде $y=I+C_ =x^ +C_ cdot frac <x^> +C_ $. Это общее решение можно представить также в виде $y=x^ +C_ cdot x^ +C_ $.

Видео:Видеоурок "Понижение порядка диф. уравнения - 2"Скачать

Дифференциальные уравнения второго порядка, не содержащие независимой переменной

Указанные дифференциальные уравнения второго порядка также допускают понижение порядка посредством замены переменных. После этого к полученным дифференциальным уравнениям первого порядка могут быть применены известные методы решения.

Дифференциальное уравнение второго порядка, не содержащее независимой переменной $x$, имеет вид $y»=fleft(y,y’right)$.

Для его решения применяют замену $y’=zleft(yright)$.

Подставляем выражения для $y’$ и $y»$ в данное дифференциальное уравнение: $zcdot frac =fleft(y,zright)$. Получили дифференциальное уравнение первого порядка относительно переменной $z$, которая является функцией $y$. Решая его, находим $zleft(yright)=phi left(y,C_ right)$.

В свою очередь, поскольку $frac =zleft(yright)$, то $frac =phi left(y,C_ right)$. Полученное дифференциальное уравнение представляет собой дифференциальное уравнение первого порядка с разделяющимися переменными, общее решение которого можно найти из выражения $int frac <phi left(y,C_right)> =x+C_ $.

Алгоритм решения дифференциального уравнения второго порядка $y»=fleft(y,y’right)$ может быть представлен в следующем виде:

1. переписываем данное дифференциальное уравнение в виде дифференциального уравнения первого порядка относительно переменной $z$, формально заменив $y»$ на $zcdot z’$, а $y’$ — на $z$;
2. полученное дифференциальное уравнение первого порядка решаем одним из подходящих известных методов;
3. найденное решение $z=phi left(y,C_ right)$ представляем в виде дифференциального уравнения первого порядка $frac=phi left(y,C_ right)$, которое является дифференциальным уравнением с разделяющимися переменными;
4. находим интеграл $I=int frac<phi left(y,C_right)> $ и получаем общее решение в виде $I=x+C_ $.

🎬 Видео

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

ДУ Уравнения, не разрешенные относительно производнойСкачать

Дифференциальные уравнения, не содержащие явно искомой функции (часть 3). Высшая математика.Скачать

Дифференциальные уравнения, не содержащие явно искомой функции (часть 1). Высшая математика.Скачать

Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

ДУ, допускающее пониж. пор. (без у)Скачать

ОДУ. 2 Линейные уравнения. Уравнение Бернулли, в полных дифференциалах. Уравнения высших порядковСкачать

Диффуры, не содержащие искомую функцию yСкачать

Дифференциальное уравнение от Бермана ★ Решите дифференциальное уравнение 2-го порядка ★ xy''=y'Скачать