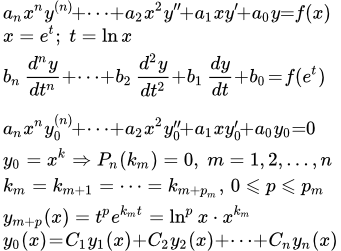Решение уравнений второго порядка методом эйлера

Более общее уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.

Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.

Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;

;
;
.

Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Решение однородного уравнения Эйлера

Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.

Рассмотрим действительные корни. Пусть k_i – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.

Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть k_i – кратный корень кратности m . Выразим комплексный корень k_i через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.

После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .

Примеры

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Решение неоднородного уравнения Эйлера

Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.

Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).

Пример

Видео:Численное решение задачи Коши методом ЭйлераСкачать

Неоднородное уравнение Эйлера со специальной неоднородной частью

Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4)
,
где – многочлены от степеней и , соответственно.

Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.

Автор: Олег Одинцов . Опубликовано: 14-08-2013 Изменено: 24-10-2020

Видео:Метод ЭйлераСкачать

Решение уравнений второго порядка методом эйлера

Численное решение линейного однородного дифференциального уравнения 2 порядка методами Эйлера и Рунге-Кутта.

Рассматривается линейное однородное дифференциальное уравнение второго порядка вида

Для того, чтобы применить к нему численные методы Эйлера и Рунге-Кутта, следует свести это уравнение к системе 2-х дифференциальных уравнений 1-го порядка

Упростим : b=b/a, c=c/a.

Вводя новую функцию x(t), получаем :

К полученной системе применяем формулу Эйлера :

Затем применяется метод Рунге-Кутта. Расчет ведется по формулам :

В случае нашей системы формулы выглядят следующим образом :

Ниже приведен пример решения уравнения 3 y”+2y’+y=0 на отрезке t=[0..1] с шагом 0,01 в среде Maple ( текст программы)

Задаются коэффициенты дифференциального уравнения

Задание начальных условий

Задание правой границы отрезка

Уменьшение шага повысит точность вычислений

Расчет числа шагов

Вывод дифференциального уравнения

ur := a * diff ( y ( t ), t $2)+ b * diff ( y ( t ), t )+ c * y ( t )=0;

Вывод начальных условий

usl := y ( t 0)= y 0; usl 2:= D ( y )( t 0)= yy 0;

Перерасчет коэффициентов к виду y «+ by ‘+ cy =0

b := b / a : c := c / a :

Применяется метод Эйлера

print (`Метод Эйлера с шагом h `= h );

for i from 1 to n do

В цикле ведется расчет по формулам Эйлера

Если в следующей строке изменить «:» на «;» будут выводится результаты расчета на каждом шаге

Применяется метод Рунге-Кутта 3 порядка

print (`Метод Рунге-Кутта 3 порядка с шагом h `= h );

Видео:19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Задачи с начальными условиями для систем обыкновенных дифференциальных уравнений

Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений $$ begin tag frac &= f_i (t, u_1, u_2, ldots, u_n), quad t > 0\ tag u_i(0) &= u_i^0, quad i = 1, 2, ldots, m. end $$

Используя векторные обозначения, задачу (1), (2) можно записать как задачу Коши $$ begin tag frac<d pmb> &= pmb(t, pmb), quad t > 0, \ tag pmb(0) &= pmb_0 end $$ В задаче Коши необходимо по известному решению в точке ( t = 0 ) необходимо найти из уравнения (3) решение при других ( t ).

Видео:ШОК! Решение ДУ методом Эйлера! ПОХИЩЕНИЕ С СЮРПРИЗОМ!Скачать

Численные методы решения задачи Коши

Существует большое количество методов численного решения задачи (3), (4). Вначале рассмотрим простейший явный метод Эйлера и его программную реализацию. Затем будут представлены методы Рунге—Кутта и многошаговые методы.

При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.

Идея численных методов решения задачи (3), (4) состоит из четырех частей:

1. Вводится расчетная сетка по переменной ( t ) (время) из ( N_t + 1 ) точки ( t_0 ), ( t_1 ), ( ldots ), ( t_ ). Нужно найти значения неизвестной функции ( pmb ) в узлах сетки ( t_n ). Обозначим через ( pmb^n ) приближенное значение ( pmb(t_n) ).

2. Предполагаем, что дифференциальное уравнение выполнено в узлах сетки.

3. Аппроксимируем производные конечными разностями.

4. Формулируем алгоритм, который вычисляет новые значения ( pmb^ ) на основе предыдущих вычисленных значений ( pmb^k ), ( k 0 ) при ( tauto 0 ).

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Явный метод Эйлера

Проиллюстрируем указанные шаги. Для начала введем расчетную сетку. Очень часто сетка является равномерной, т.е. имеет одинаковое расстояние между узлами ( t_n ) и ( t_ ): $$ omega_tau = . $$

Затем, предполагаем, что уравнение выполнено в узлах сетки, т.е.: $$ pmb^prime (t_n) = pmb(t_n, u(t_n)), quad t_n in omega_tau. $$

Заменяем производные конечными разностями. С этой целью, нам нужно знать конкретные формулы, как производные могут быть аппроксимированы конечными разностями. Простейший подход заключается в использовании определения производной: $$ pmb^prime(t) = lim_ frac<pmb(t+tau) — pmb(t)>. $$

В произвольном узле сетки ( t_n ) это определение можно переписать в виде: $$ begin pmb^prime(t_n) = lim_ frac<pmb(t_n+tau) — pmb(t_n)>. end $$ Вместо того, чтобы устремлять шаг сетки к нулю, мы можем использовать малый шаг ( tau ), который даст численное приближение ( u^prime(t_n) ): $$ begin pmb^prime(t_n) approx frac<pmb^ — pmb^>. end $$ Такая аппроксимация известна как разностная производная вперед и имеет первый порядок по ( tau ), т.е. ( O(tau) ). Теперь можно использовать аппроксимацию производной. Таким образом получим явный метод Эйлера: $$ begin tag frac<pmb^ — pmb^n> = pmb(t_n, pmb^). end $$

Четвертый шаг заключается в получении численного алгоритма. Из (5) следует, что мы должны знать значение ( y^n ) для того, чтобы решить уравнение (5) относительно ( y^ ) и получить формулу для нахождения приближенного значения искомой функции на следующем временном слое ( t_ ): $$ begin tag pmb^ = pmb^n + tau pmb(t_n, pmb^) end $$

При условии, что у нас известно начальное значение ( pmb^0 = pmb_0 ), мы можем использовать (6) для нахождения решений на последующих временных слоях.

Программная реализация явного метода Эйлера

Выражение (6) может быть как скалярным так и векторным уравнением. И в скалярном и в векторном случае на языке Python его можно реализовать следующим образом

При решении системы (векторный случай), u[n] — одномерный массив numpy длины ( m+1 ) (( m ) — размерность задачи), а функция F должна возвращать numpy -массив размерности ( m+1 ), t[n] — значение в момент времени ( t_n ).

Таким образом численное решение на отрезке ( [0, T] ) должно быть представлено двумерным массивом, инициализируемым нулями u = np.zeros((N_t+1, m+1)) . Первый индекс соответствует временному слою, а второй компоненте вектора решения на соответствующем временном слое. Использование только одного индекса, u[n] или, что то же самое, u[n, :] , соответствует всем компонентам вектора решения.

Функция euler решения системы уравнений реализована в файле euler.py:

Строка F_ = lambda . требует пояснений. Для пользователя, решающего систему ОДУ, удобно задавать функцию правой части в виде списка компонент. Можно, конечно, требовать чтобы пользователь возвращал из функции массив numpy , но очень легко осуществлять преобразование в самой функции решателе. Чтобы быть уверенным, что результат F будет нужным массивом, который можно использовать в векторных вычислениях, мы вводим новую функцию F_ , которая вызывает пользовательскую функцию F «прогоняет» результат через функцию assaray модуля numpy .

Видео:Дифференциальное уравнение. Формула ЭйлераСкачать

Неявный метод Эйлера

При построении неявного метода Эйлера значение функции ( F ) берется на новом временном слое, т.е. для решении задачи (5) используется следующий метод: $$ begin tag frac<pmb^ — pmb^n> = pmb(t_, pmb^). end $$

Таким образом для нахождения приближенного значения искомой функции на новом временном слое ( t_ ) нужно решить нелинейное уравнение относительно ( pmb^ ): $$ begin tag pmb^ — tau pmb(t_, pmb^) — y^n = 0. end $$

Для решения уравнения (8) можно использовать, например, метод Ньютона.

Программная реализация неявного метода Эйлера

Функция backward_euler решения системы уравнений реализована в файле euler.py:

Отметим, что для нахождения значения u[n+1] используется функция fsolve модуля optimize библиотеки scipy . В качестве начального приближения для решения нелинейного уравнения используется значение искомой функции с предыдущего слоя u[n] .

Видео:15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Методы Рунге—Кутта

Одношаговый метод Рунге—Кутта в общем виде записывается следующим образом: $$ begin tag frac<pmb^ — pmb^n> = sum_^s b_i pmb_i, end $$ где $$ begin tag pmb_i = pmbleft( t_n + c_itau, pmb^n + tau sum_^s a_pmb_j right), quad i = 1, 2, ldots, s. end $$ Формула (9) основана на ( s ) вычислениях функции ( pmb ) и называется ( s )-стадийной. Если ( a_ = 0 ) при ( j geq i ) имеем явный метод Рунге—Кутта. Если ( a_ = 0 ) при ( j > i ) и ( a_ ne 0 ), то ( pmb_i ) определяется неявно из уравнения $$ begin tag pmb_i = pmbleft( t_n + c_itau, pmb^n + tau sum_^ a_pmb_j + tau a_ pmb_i right), quad i = 1, 2, ldots, s. end $$ О таком методе Рунге—Кутта говорят как о диагонально-неявном.

Одним из наиболее распространенных является явный метод Рунге-Кутта четвертого порядка: $$ begin tag pmb_1 & = pmb(t_n, pmb^n), &quad pmb_2 &= pmbleft( t_n + frac, pmb^n + tau frac<pmb_1> right),\ pmb_3 &= pmbleft( t_n + frac, pmb^n + tau frac<pmb_2> right), &quad pmb_4 &= pmbleft( t_n + tau, pmb^n + tau pmb_3 right),\ frac<pmb^ -pmb^n> &= frac (pmb_1 + 2pmb_2 + 2pmb_3 + pmb_4) & & end $$

Видео:Метод Эйлера. Решение систем ДУСкачать

Многошаговые методы

В методах Рунге—Кутта в вычислениях участвуют значения приближенного решения только в двух соседних узлах ( pmb^n ) и ( pmb^ ) — один шаг по переменной ( t ). Линейный ( m )-шаговый разностный метод записывается в виде $$ begin tag frac sum_^m a_i pmb^ = sum_^ b_i pmb(t_, pmb^), quad n = m-1, m, ldots end $$ Вариант численного метода определяется заданием коэффициентов ( a_i ), ( b_i ), ( i = 0, 1, ldots, m ), причем ( a_0 ne 0 ). Для начала расчетов по рекуррентной формуле (13) необходимо задать ( m ) начальных значений ( pmb^0 ), ( pmb^1 ), ( dots ), ( pmb^ ) (например, можно использовать для их вычисления метод Эйлера).

Различные варианты многошаговых методов (методы Адамса) решения задачи с начальными условиями для систем обыкновенных дифференциальных уравнений могут быть получены на основе использования квадратурных формул для правой части равенства $$ begin tag pmb(t_) — pmb(t_n) = int_^<t_> pmb(t, pmb) dt end $$

Для получения неявного многошагового метода используем для подынтегральной функции интерполяционную формулу по значениям функции ( pmb^ = pmb(t_, pmb^) ), ( pmb^n ), ( dots ), ( pmb^ ), т.е. $$ begin tag frac<pmb^ — pmb^n> = sum_^ b_i pmb(t_, pmb^) end $$

Для интерполяционного метода Адамса (15) наивысший порядок аппроксимации равен ( m+1 ).

Для построения явных многошаговых методов можно использовать процедуру экстраполяции подынтегральной функции в правой части (14). В этом случае приближение осуществляется по значениям ( pmb^n ), ( pmb^ ), ( dots ), ( pmb^ ) и поэтому $$ begin tag frac<pmb^ — pmb^n> = sum_^ b_i pmb(t_, pmb^) end $$

Для экстраполяционного метода Адамса (16) погрешность аппроксимации имеет ( m )-ый порядок.

На основе методов Адамса строятся и схемы предиктор–корректор. На этапе предиктор используется явный метод Адамса, на этапе корректора — аналог неявного метода Адамса. Например, при использовании методов третьего порядка аппроксимации в соответствии с (18) для предсказания решения положим $$ frac<pmb^ — pmb^n> = frac (23 pmb^ -16pmb^ + 5pmb^). $$ Для уточнеия решения (см. (17)) используется схема $$ frac<pmb^ — pmb^n> = frac (9pmb^ + 19pmb^ — 5pmb^ + pmb^). $$ Аналогично строятся и другие классы многошаговых методов.

Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Жесткие системы ОДУ

При численном решении задачи Коши для систем обыкновенных дифференциальных уравнений (3), (4) могут возникнуть дополнительные трудности, порожденные жесткостью системы. Локальные особенности поведения решения в точке ( u = w ) передаются линейной системой $$ begin frac

= sum_^ frac (t, w) v + bar(t), quad t > 0. end $$

Пусть ( lambda_i(t) ), ( i = 1, 2, ldots, m ) — собственные числа матрицы $$ begin A(t) = < a_(t) >, quad a_(t) = frac(t, w). end $$ Система уравнений (3) является жесткой, если число $$ begin S(t) = frac <max_|Re lambda_i(t)|> <min_|Re lambda_i(t)|> end $$ велико. Это означает, что в решении присутствуют составляющие с сильно различающимися масштабами изменения по переменной ( t ).

Для численное решения жестких задач используются вычислительные алгоритмы, которые имеют повышенный запас устойчивости. Необходимо ориентироваться на использование ( A )-устойчивых или ( A(alpha) )-устойчивых методов.

Метод называется ( A )-устойчивым, если при решении задачи Коши для системы (3) область его устойчивости содержит угол $$ begin |arg(-mu)| —>

📹 Видео

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать

метод Эйлера для решения ОДУСкачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

МЗЭ 2022 Численное решение дифференциальных уравнений Метод Эйлера Ложкин С. А.Скачать